2.3: Tempo, velocidade e velocidade

Last updated
Save as PDF

Page ID: 194270

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

objetivos de aprendizagem

Ao final desta seção, você poderá:

Explique as relações entre velocidade instantânea, velocidade média, velocidade instantânea, velocidade média, deslocamento e tempo.
Calcule a velocidade e a velocidade dadas a posição inicial, o tempo inicial, a posição final e o tempo final.
Derive um gráfico de velocidade versus tempo, dado um gráfico de posição versus tempo.
Interprete um gráfico de velocidade versus tempo.

O movimento é mais do que a distância e o deslocamento. Perguntas como: “Quanto tempo dura uma corrida a pé?” e “Qual foi a velocidade do corredor?” não pode ser respondida sem a compreensão de outros conceitos. Nesta seção, adicionamos definições de tempo, velocidade e velocidade para expandir nossa descrição do movimento.

Os caracóis que deixam rastros de lodo enquanto correm entre si ao longo de uma superfície plana. — Figura\(\PageIndex{1}\): O movimento desses caracóis de corrida pode ser descrito por suas velocidades e velocidades. (crédito: tobitasflickr, Flickr)

Hora

Conforme discutido em Quantidades e Unidades Físicas, as quantidades físicas mais fundamentais são definidas pela forma como são medidas. Esse é o caso do tempo. Cada medição do tempo envolve medir uma mudança em alguma quantidade física. Pode ser um número em um relógio digital, um batimento cardíaco ou a posição do Sol no céu. Em física, a definição de tempo é simples: tempo é mudança, ou o intervalo no qual a mudança ocorre. É impossível saber que o tempo passou, a menos que algo mude.

A quantidade de tempo ou alteração é calibrada em comparação com um padrão. A unidade SI para o tempo é a segunda, abreviada s. Podemos, por exemplo, observar que um determinado pêndulo faz um giro completo a cada 0,75 s. Poderíamos então usar o pêndulo para medir o tempo contando suas oscilações ou, é claro, conectando o pêndulo a um mecanismo de relógio que registra a hora em um mostrador. Isso nos permite não apenas medir a quantidade de tempo, mas também determinar uma sequência de eventos.

Como o tempo se relaciona com o movimento? Geralmente estamos interessados no tempo decorrido para um movimento específico, como quanto tempo um passageiro de avião leva para ir de seu assento até a parte de trás do avião. Para encontrar o tempo decorrido, notamos o tempo no início e no final do movimento e subtraímos os dois. Por exemplo, uma aula pode começar às 11h e terminar às 11h50, de forma que o tempo decorrido seja de 50 min. O tempo decorrido\(Δt\) é a diferença entre a hora de término e a hora de início,

\(Δt=t_f−t_0\),

onde\(Δt\) está a mudança no tempo ou no tempo decorrido,\(t_f\) é o tempo no final do movimento e\(t_0\) é o tempo no início do movimento. (Como de costume, o símbolo delta\(Δ\),, significa a mudança na quantidade que o segue.)

A vida é mais simples se a hora de início\(t_0\) for considerada zero, como quando usamos um cronômetro. Se estivéssemos usando um cronômetro, ele simplesmente mostraria zero no início da palestra e 50 minutos no final. Se\(t_0=0\), então

\[Δt=t_f≡t.\]

Neste texto, por uma questão de simplicidade,

o movimento começa em um tempo igual a zero (\(t_0=0\))
o símbolo\(t\) é usado para o tempo decorrido, a menos que especificado de outra forma (\(Δt=t_f≡t\))

Velocidade

Sua noção de velocidade é provavelmente a mesma de sua definição científica. Você sabe que se você tem um grande deslocamento em um pequeno período de tempo, você tem uma grande velocidade, e essa velocidade tem unidades de distância divididas pelo tempo, como milhas por hora ou quilômetros por hora.

Definição: VELOCIDADE MÉDIA

A velocidade média é o deslocamento (mudança de posição) dividido pelo tempo de viagem,

\[\bar{v}=\frac{Δx}{Δt}=\frac{x_f−x_0}{t_f−t_0}.\]

onde\(\bar{v}\) é a velocidade média (indicada pela barra sobre a\(v\)),\(Δx\) é a mudança na posição (ou deslocamento)\(x_f\) e\(x_0\) são as posições final e inicial às vezes\(t_f\) e\(t_0\), respectivamente. Se a hora de início\(t_0\) for considerada zero, a velocidade média será simplesmente

\[\bar{v}=\frac{Δx}{t}.\]

Observe que essa definição indica que a velocidade é um vetor porque o deslocamento é um vetor. Tem magnitude e direção. A unidade SI para velocidade é metros por segundo ou m/s, mas muitas outras unidades, como km/h, mi/h (também escrito como mph) e cm/s, são de uso comum. Suponha, por exemplo, que um passageiro de avião tenha levado 5 segundos para se mover −4 m (o sinal negativo indica que o deslocamento está em direção à parte de trás do avião). Sua velocidade média seria

\[\bar{v}=\frac{Δx}{t}=\frac{−4\,m}{5\,s}=−0.8 \,m/s.\]

O sinal de menos indica que a velocidade média também está na parte traseira do avião.

No entanto, a velocidade média de um objeto não nos diz nada sobre o que acontece com ele entre o ponto inicial e o ponto final. Por exemplo, não podemos dizer pela velocidade média se o passageiro do avião para momentaneamente ou recua antes de ir para a parte de trás do avião. Para obter mais detalhes, devemos considerar segmentos menores da viagem em intervalos de tempo menores.

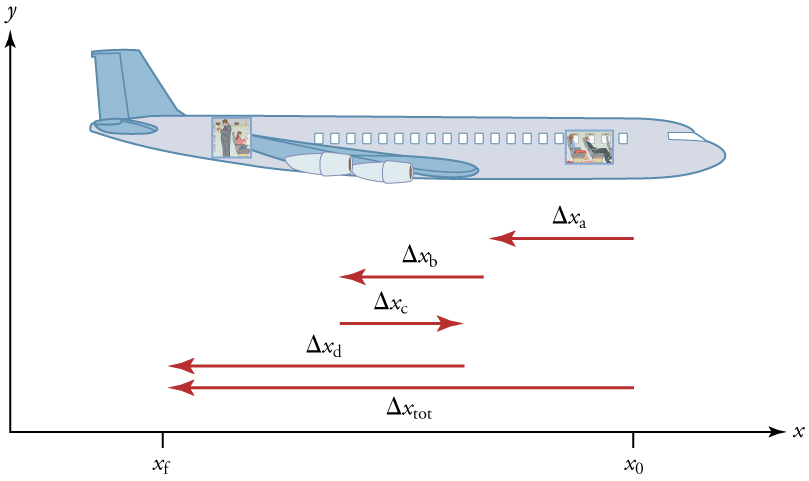
Avião mostrado de fora. As setas vetoriais mostram os caminhos de cada segmento individual da viagem do passageiro até a parte de trás do avião. — Figura\(\PageIndex{2}\): Um registro mais detalhado de um passageiro de avião indo em direção à parte de trás do avião, mostrando trechos menores de sua viagem.

Quanto menores os intervalos de tempo considerados em um movimento, mais detalhadas são as informações. Quando levamos esse processo à sua conclusão lógica, ficamos com um intervalo infinitesimalmente pequeno. Nesse intervalo, a velocidade média se torna a velocidade instantânea ou a velocidade em um instante específico. O velocímetro de um carro, por exemplo, mostra a magnitude (mas não a direção) da velocidade instantânea do carro. (A polícia distribui multas com base na velocidade instantânea, mas ao calcular quanto tempo levará para ir de um lugar a outro em uma viagem rodoviária, você precisa usar a velocidade média.) A velocidade instantânea\(v\) é a velocidade média em um instante específico no tempo (ou em um intervalo de tempo infinitesimalmente pequeno).

Matematicamente, encontrar a velocidade instantânea\(v\), em um instante preciso,\(t\) pode envolver tomar um limite, uma operação de cálculo além do escopo deste texto. No entanto, sob muitas circunstâncias, podemos encontrar valores precisos para a velocidade instantânea sem cálculo.

Rapidez

Na linguagem cotidiana, a maioria das pessoas usa os termos “velocidade” e “velocidade” de forma intercambiável. Em física, no entanto, eles não têm o mesmo significado e são conceitos distintos. Uma grande diferença é que a velocidade não tem direção. Portanto, a velocidade é um escalar. Assim como precisamos distinguir entre velocidade instantânea e velocidade média, também precisamos distinguir entre velocidade instantânea e velocidade média.

A velocidade instantânea é a magnitude da velocidade instantânea. Por exemplo, suponha que o passageiro do avião em um instante tenha uma velocidade instantânea de −3,0 m/s (o significado negativo na parte traseira do avião). Ao mesmo tempo, sua velocidade instantânea era de 3,0 m/s. Ou suponha que, em um determinado momento, durante uma viagem de compras, sua velocidade instantânea seja de 40 km/h em direção ao norte. Sua velocidade instantânea nesse instante seria de 40 km/h, a mesma magnitude, mas sem direção. A velocidade média, no entanto, é muito diferente da velocidade média. A velocidade média é a distância percorrida dividida pelo tempo decorrido.

Observamos que a distância percorrida pode ser maior do que o deslocamento. Portanto, a velocidade média pode ser maior que a velocidade média, que é o deslocamento dividido pelo tempo. Por exemplo, se você dirige até uma loja e volta para casa em meia hora e o odômetro do seu carro mostra que a distância total percorrida foi de 6 km, sua velocidade média foi de 12 km/h. Sua velocidade média, entretanto, foi zero, porque seu deslocamento para a viagem de ida e volta é zero. (O deslocamento é uma mudança de posição e, portanto, é zero para uma viagem de ida e volta.) Assim, a velocidade média não é simplesmente a magnitude da velocidade média.

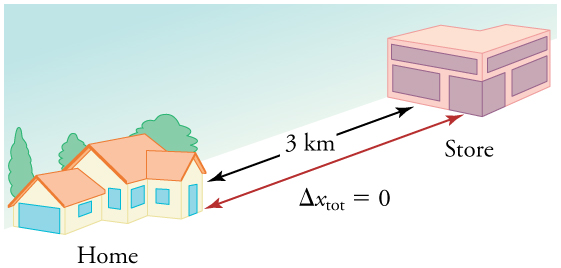
Uma casa e uma loja, com um conjunto de setas no meio, mostrando que a distância entre elas é de 3 pontos 0 quilômetros e a distância total percorrida, delta x total, é igual a 0 quilômetros. — Figura\(\PageIndex{3}\): Durante uma viagem de ida e volta de 30 minutos até a loja, a distância total percorrida é de 6 km. A velocidade média é de 12 km/h. O deslocamento para a viagem de ida e volta é zero, pois não houve mudança líquida na posição. Assim, a velocidade média é zero.

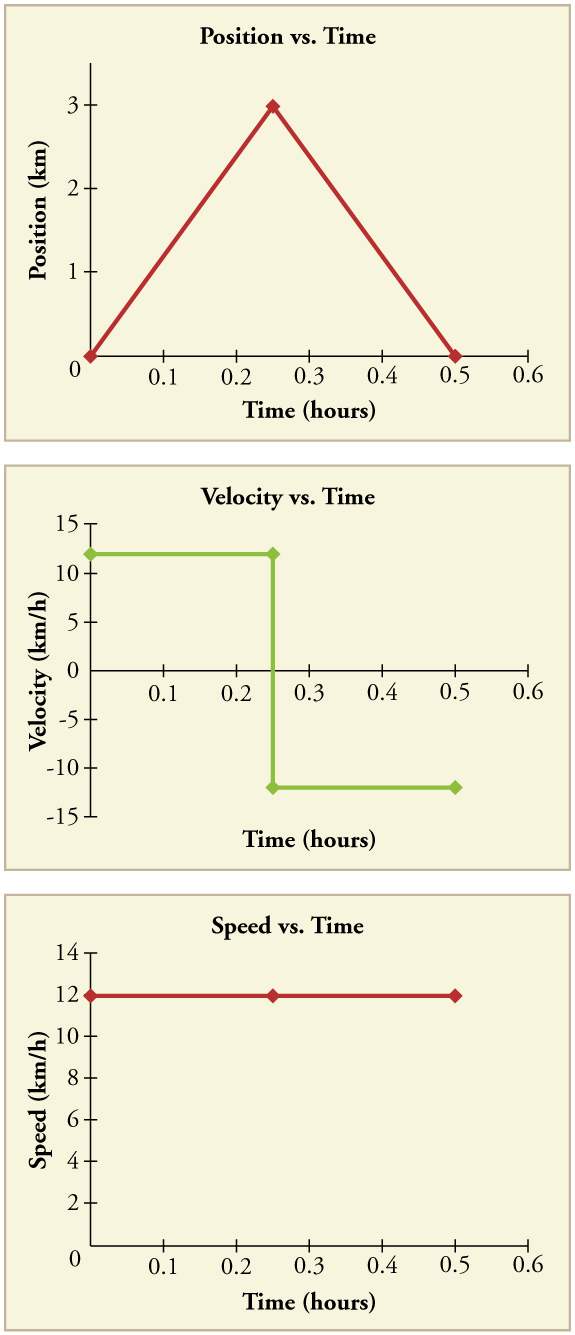
Outra forma de visualizar o movimento de um objeto é usar um gráfico. Um gráfico da posição ou da velocidade em função do tempo pode ser muito útil. Por exemplo, para essa ida à loja, a posição, a velocidade e a velocidade versus. Os gráficos de tempo são exibidos na Figura\(\PageIndex{4}\). (Note que esses gráficos retratam um modelo muito simplificado da viagem. Estamos assumindo que a velocidade é constante durante a viagem, o que não é realista, já que provavelmente vamos parar na loja. Mas, por uma questão de simplicidade, vamos modelá-lo sem paradas ou mudanças na velocidade. Também estamos assumindo que a rota entre a loja e a casa é uma linha perfeitamente reta.)

Gráficos de três linhas. O gráfico da primeira linha é da posição em quilômetros versus o tempo em horas. A linha aumenta linearmente de 0 quilômetros para 6 quilômetros nas primeiras 0 ponto 25 horas. Em seguida, diminui linearmente de 6 quilômetros para 0 quilômetros entre 0 ponto 25 e 0 ponto 5 horas. O gráfico da segunda linha mostra a velocidade em quilômetros por hora versus o tempo em horas. A linha é plana a 12 quilômetros por hora, do tempo 0 ao tempo 0, ponto 25. É vertical no tempo 0 ponto 25, caindo de 12 quilômetros por hora para menos 12 quilômetros por hora. É plano novamente a menos 12 quilômetros por hora, de 0 ponto 25 horas a 0 ponto 5 horas. O gráfico da terceira linha mostra a velocidade em quilômetros por hora versus o tempo em horas. A linha é plana a 12 quilômetros por hora, desde o tempo igual a 0 até o tempo igual a 0 ponto 5 horas. — Figura\(\PageIndex{4}\): Posição versus tempo, velocidade versus tempo e velocidade versus tempo em uma viagem. Observe que a velocidade da viagem de volta é negativa.

FAZENDO CONEXÕES: INVESTIGAÇÃO PARA LEVAR PARA CASA - TENDO UMA NOÇÃO DA VELOCIDADE

Se você passou muito tempo dirigindo, provavelmente tem uma boa noção de velocidades entre cerca de 10 e 70 milhas por hora. Mas o que são esses em metros por segundo? O que queremos dizer quando dizemos que algo está se movendo a 10 m/s? Para ter uma ideia melhor do que esses valores realmente significam, faça algumas observações e cálculos sozinho:

calcule as velocidades típicas dos carros em metros por segundo
estime a velocidade de corrida e caminhada cronometrando você mesmo; converta as medidas em m/s e mi/h
determine a velocidade de uma formiga, caracol ou folha caindo

Exercício\(\PageIndex{1}\)

Um trem suburbano viaja de Baltimore para Washington, DC, e volta em 1 hora e 45 minutos. A distância entre as duas estações é de aproximadamente 40 milhas. O que é

a velocidade média do trem, e
a velocidade média do trem em m/s?

Resposta

(a) A velocidade média do trem é zero porque\(x_f=x_0\); o trem acaba no mesmo lugar em que começa.

(b) A velocidade média do trem é calculada abaixo. Observe que o trem viaja 40 milhas para um lado e 40 milhas para trás, para uma distância total de 80 milhas.

\(\frac{distance}{time}=\frac{80 miles}{105 minutes}\)

\(\frac{80 miles}{105 minutes}×\frac{5280 feet}{1 mile}×\frac{1 meter}{3.28 feet}×\frac{1 minute}{60 seconds}=20 m/s\)

Resumo

O tempo é medido em termos de mudança, e sua unidade SI é o segundo (s). O tempo decorrido para um evento\(t_f\) é\[Δt=t_f−t_0 \nonumber,\] onde está o tempo final e\(t_0\) o tempo inicial. O tempo inicial geralmente é considerado zero, como se fosse medido com um cronômetro; o tempo decorrido é então justo\(t\).
A velocidade média\(\bar{v}\) é definida como o deslocamento dividido pelo tempo de viagem. Em símbolos, a velocidade média é\[\bar{v}=\frac{Δx}{Δt}=\frac{x_f−x_0}{t_f−t_0} \nonumber.\]
A unidade SI para velocidade é m/s.
A velocidade é um vetor e, portanto, tem uma direção.
A velocidade instantânea\(v\) é a velocidade em um instante específico ou a velocidade média para um intervalo infinitesimal.
A velocidade instantânea é a magnitude da velocidade instantânea.
A velocidade instantânea é uma quantidade escalar, pois não tem direção especificada.
A velocidade média é a distância total percorrida dividida pelo tempo decorrido. (A velocidade média não é a magnitude da velocidade média.) A velocidade é uma quantidade escalar; não tem direção associada a ela.

Glossário

velocidade média: distância percorrida dividida pelo tempo durante o qual o movimento ocorre

velocidade média: deslocamento dividido pelo tempo durante o qual o deslocamento ocorre

velocidade instantânea: velocidade em um instante específico ou a velocidade média em um intervalo de tempo infinitesimal

velocidade instantânea: magnitude da velocidade instantânea

hora: mudança ou o intervalo no qual a mudança ocorre

modelo: descrição simplificada que contém somente os elementos necessários para descrever a física de uma situação física

tempo decorrido: a diferença entre a hora de término e a hora de início