4.8 : Fonctions graphiques (sans utiliser le calcul)
- Page ID
- 165738
Il existe certaines fonctions de base, appelées fonctions de la boîte à outils, que les élèves devraient reconnaître à l'aide de leur définition de fonction et de leur graphique. Pour chacune de ces fonctions,\(x\) est la variable d'entrée et\(f(x)\) est la variable de sortie. Les graphiques suivants sont extraits du manuel OER Business Calculus de Calaway, Hoffman et Lippman, 2013 et sont utilisés avec autorisation (Creative Commons Attribution 3.0 United States License).


Contrairement au cours STEM Calculus I traditionnel, ce cours de calcul pour les affaires et les sciences sociales n'enseigne pas les fonctions graphiques à l'aide de transformations de fonctions.
Les étudiants de cette classe sont censés créer un tableau de solutions et représenter graphiquement la fonction. Les élèves apprendront également à représenter graphiquement des fonctions à l'aide de Calculus !
Représenter graphiquement les fonctions suivantes :
- \(f(x) = \sqrt[3]{x}\)
- \(f(x) = \dfrac{1 }{x^2 − 3}\)
Solution
- Créez un tableau de solutions et définissez le domaine de la fonction.
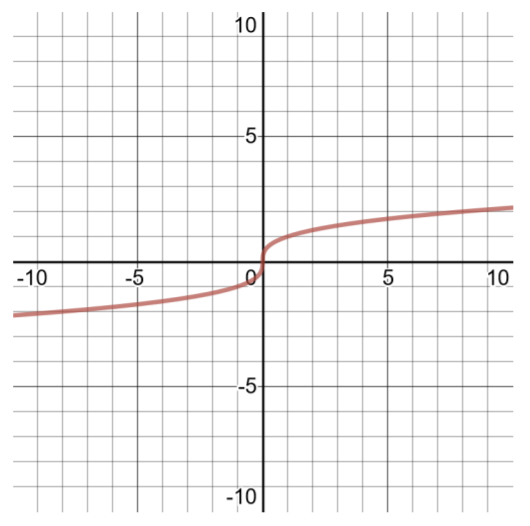
| Tableau des solutions pour le\(f(x) =\sqrt[3]{x}\) domaine\((−\infty , \infty )\) | |
| \(x\) | \(f(x)\) |
| -8 | -2 |
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
| 8 | 2 |
- Créez un tableau de solutions et définissez le domaine de la fonction. Pour identifier le domaine de cette fonction rationnelle, faites attention au dénominateur. Le dénominateur ne peut pas être égal à 0. Définissez le dénominateur = 0 pour résoudre x et trouver les valeurs qui ne seront pas autorisées pour x.
\(\begin{aligned} f(x) &= \dfrac{1 }{x^2 − 3}\\ 0 &= x^2 − 3 \\3 &= x^2 \\ \pm \sqrt{3} &=\sqrt{x^2} \\ \pm \sqrt{3}& = x \end{aligned}\)
Ces nombres doivent être exclus du domaine de cette fonction\(−\sqrt{3}\) (environ −1,732)) et\(\sqrt{3}\) (environ 1,732)).
Pour représenter correctement cette fonction, il est important d'examiner le comportement de ces nombres exclus du domaine. D'où la raison de tant de paires ordonnées dans le tableau des solutions. Réfléchissez ainsi : commencez par un domaine de\((−\infty , \infty )\), mais vous devez supprimer tous les nombres qui poseront des problèmes (comme dans ce cas, les nombres qui feront en sorte que le dénominateur de la fonction soit 0, car la division par 0 n'est pas définie). Il est très fastidieux de représenter graphiquement de telles fonctions à la main, mais c'est une compétence importante pour un étudiant qui souhaite réussir en calcul pour les sciences commerciales et sociales.
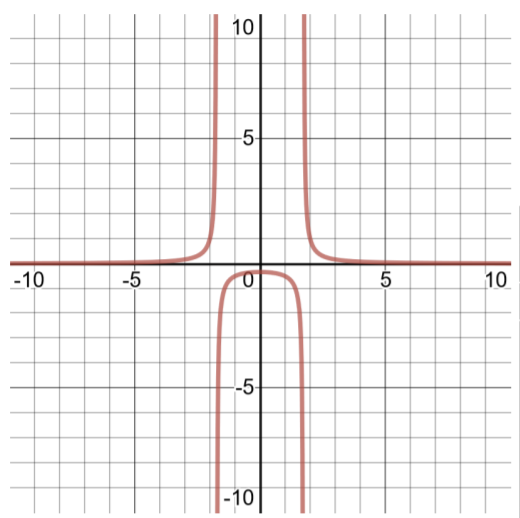
| Tableau des solutions pour le\(f(x) = \sqrt[3]{ x}\) domaine\((−\infty , \infty )\) | |
| \(x\) | \(f(x)\) |
| -4 | 0,077 |
| -3 | 0,167 |
| -2 | 1 |
| -1,5 | -1,333 |
| -1 | -0,5 |
| -0,5 | -0,364 |
| 0 | 0 |
| 0,5 | -0,364 |
| 1 | -0,5 |
| 1,5 | -1,333 |
| 2 | 1 |
| 3 | 0,167 |
| 4 | 0,077 |
Problèmes pratiques : Représentez graphiquement les fonctions suivantes, en prêtant attention au domaine de la fonction.
- \(f(x) = 2x^3\)
- \(f(x) = \dfrac{1 }{2x^2}\)
- \(f(x) = 4 \vert x − 2 \vert\)
- \(f(x) = \dfrac{1 }{3} x − 12 \)
- \(f(x) = \dfrac{1 }{x − 7}\)
- \(f(x) = 3\sqrt{2x^3 + 1}\)


