8.2 : Énergie potentielle d'un système
- Page ID
- 191601
- Associez la différence d'énergie potentielle au travail effectué sur une particule pour un système sans friction ni traînée d'air
- Expliquer la signification du zéro de la fonction énergétique potentielle d'un système
- Calculer et appliquer l'énergie potentielle gravitationnelle d'un objet proche de la surface de la Terre et l'énergie potentielle élastique d'un système masse-ressort
Dans Work, nous avons vu que le travail effectué sur un objet par la force gravitationnelle constante, près de la surface de la Terre, lors d'un déplacement quelconque est fonction uniquement de la différence entre les positions des points extrêmes du déplacement. Cette propriété nous permet de définir pour le système un type d'énergie différent de son énergie cinétique, appelée énergie potentielle. Nous examinons différentes propriétés et types d'énergie potentielle dans les sous-sections suivantes.
Les bases du potentiel énergétique
Dans Motion in Two and Three Dimensions, nous avons analysé le mouvement d'un projectile, comme si vous donniez un coup de pied à un ballon de football dans Figure\(\PageIndex{1}\). Pour cet exemple, ignorons la friction et la résistance à l'air. Lorsque le ballon s'élève, le travail effectué par la force gravitationnelle sur le ballon est négatif, car le déplacement du ballon est positif verticalement et la force due à la gravité est négative verticalement. Nous avons également remarqué que la balle ralentissait jusqu'à ce qu'elle atteigne son point le plus élevé du mouvement, diminuant ainsi son énergie cinétique. Cette perte d'énergie cinétique se traduit par un gain d'énergie potentielle gravitationnelle du système Football-Terre.
Alors que le ballon tombe vers la Terre, le travail effectué sur le ballon est désormais positif, car le déplacement et la force gravitationnelle pointent tous deux verticalement vers le bas. La balle accélère également, ce qui indique une augmentation de l'énergie cinétique. Par conséquent, l'énergie potentielle gravitationnelle est reconvertie en énergie cinétique.
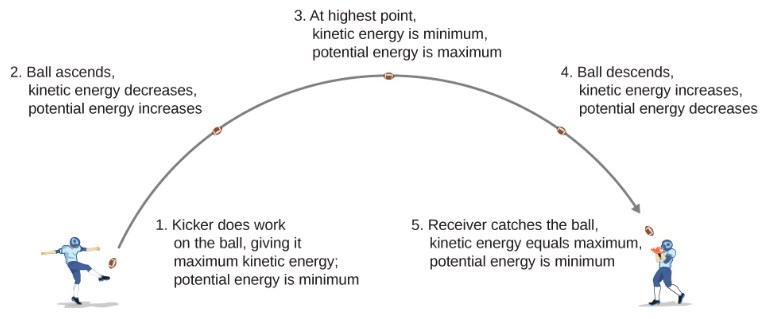
Sur la base de ce scénario, nous pouvons définir la différence d'énergie potentielle entre le point A et le point B comme étant le négatif du travail effectué :
\[ \Delta U_{A B}=U_{B}-U_{A}=-W_{A B} \label{8.1} \]
Cette formule indique explicitement une différence d'énergie potentielle, et pas seulement une énergie potentielle absolue. Par conséquent, nous devons définir l'énergie potentielle à une position donnée de manière à énoncer des valeurs standard de l'énergie potentielle par elles-mêmes, plutôt que des différences d'énergie potentielles. Pour ce faire, nous réécrivons la fonction énergétique potentielle en termes de constante arbitraire,
\[ \Delta U=U(\overrightarrow{\mathbf{r}})-U\left(\overrightarrow{\mathbf{r}}_{0}\right) \label{8.2} \]
Le choix de l'énergie potentielle à un point de départ de\(\vec{r}_0\) est fait par souci de commodité pour le problème posé. Plus important encore, quel que soit le choix fait, il doit être indiqué et maintenu de manière cohérente tout au long du problème. Il existe des choix bien acceptés en matière d'énergie potentielle initiale. Par exemple, la hauteur la plus basse d'un problème est généralement définie comme une énergie potentielle nulle, ou si un objet se trouve dans l'espace, le point le plus éloigné du système est souvent défini comme une énergie potentielle nulle. Alors, l'énergie potentielle, par rapport à zéro à\(\vec{r}_0\), est juste\(U(\vec{r})\).
Tant qu'il n'y a pas de friction ou de résistance à l'air, la variation de l'énergie cinétique du ballon est négative par rapport à la variation de l'énergie potentielle gravitationnelle du ballon. Cela peut être généralisé à n'importe quelle énergie potentielle :
\[\Delta K_{A B}=-\Delta U_{A B} \label{8.3}\]
Prenons un exemple précis, en choisissant une énergie potentielle nulle pour l'énergie potentielle gravitationnelle à des points appropriés.
Une particule se déplace le long de l'axe x sous l'action d'une force donnée par F = -ax 2, où a = 3 N/m 2. (a) Quelle est la différence entre son énergie potentielle lorsqu'elle passe de x A = 1 m à x B = 2 m ? (b) Quelle est l'énergie potentielle de la particule à x = 1 m par rapport à 0,5 J d'énergie potentielle donnée à x=0 ?
Stratégie
(a) La différence d'énergie potentielle est la valeur négative du travail effectué, telle que définie par l'équation \ ref {8.1}. Le travail est défini dans le chapitre précédent comme le produit scalaire de la force avec la distance. Comme la particule avance dans la direction x, le produit scalaire se simplifie en une multiplication (\(\hat{i} \cdot \hat{i}\)= 1). Pour déterminer le travail total effectué, nous devons intégrer la fonction entre les limites données. Après intégration, nous pouvons indiquer le travail ou l'évolution de l'énergie potentielle. (b) La fonction d'énergie potentielle, par rapport à zéro à x=0, est l'intégrale indéfinie rencontrée dans la partie (a), la constante d'intégration étant déterminée à partir de l'équation \ ref {8.3}. Ensuite, nous substituons la valeur x à la fonction de l'énergie potentielle pour calculer l'énergie potentielle à x = 1.
Solution
a. Le travail effectué par la force donnée lorsque la particule se déplace de la coordonnée x à x + dx dans une dimension est
\[d W=\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=F d x=-a x^{2} d x \nonumber \]
En substituant cette expression dans l'équation \ ref {8.1}, nous obtenons
\[\Delta U=-W=\int_{x_{1}}^{x_{2}} a x^{2} d x=\left.\frac{1}{3}\left(3 \: \mathrm{N} / \mathrm{m}^{2}\right) x^{3}\right|_{1 \mathrm{m}} ^{2\mathrm{m}}=7 \: \mathrm{J} \nonumber \]
b. L'intégrale indéfinie de la fonction énergétique potentielle dans la partie (a) est
\[U(x)=\frac{1}{3} a x^{3}+\text { const. }, \nonumber \]
et nous voulons que la constante soit déterminée par
\[ U(0) = 0.5 \: J. \nonumber \]
Ainsi, l'énergie potentielle par rapport à zéro à x = 0 est juste
\[U(x)=\frac{1}{3} a x^{3}+0.5 \: \mathrm{J} \nonumber \]
Par conséquent, l'énergie potentielle à x = 1 m est
\[U(1 \: \mathrm{m})=\frac{1}{3}\left(3 \: \mathrm{N} / \mathrm{m}^{2}\right)(1 \: \mathrm{m})^{3}+0.5 \: \mathrm{J}=1.5 \: \mathrm{J}. \nonumber \]
L'importance
Dans cet exemple unidimensionnel, toute fonction que nous pouvons intégrer, indépendamment du chemin, est conservatrice. Remarquez comment nous avons appliqué la définition de la différence d'énergie potentielle pour déterminer la fonction énergétique potentielle par rapport à zéro à un point choisi. Notez également que l'énergie potentielle, telle que déterminée dans la partie (b), à x = 1 m est U (1 m) = 1 J et à x = 2 m est U (2 m) = 8 J ; leur différence est le résultat dans la partie (a).
Dans l'exemple\(\PageIndex{1}\), quelles sont les énergies potentielles de la particule à x = 1 m et x = 2 m par rapport à zéro à x = 1,5 m ? Vérifiez que la différence d'énergie potentielle est toujours de 7 J.
Systèmes à plusieurs particules
En général, un système d'intérêt peut être constitué de plusieurs particules. La différence d'énergie potentielle du système est la négation du travail effectué par les forces gravitationnelles ou élastiques, qui, comme nous le verrons dans la section suivante, sont des forces conservatrices. La différence d'énergie potentielle dépend uniquement des positions initiale et finale des particules et de certains paramètres qui caractérisent l'interaction (comme la masse pour la gravité ou la constante de ressort pour une force de loi de Hooke).
Il est important de se rappeler que l'énergie potentielle est une propriété des interactions entre les objets dans un système choisi, et pas seulement une propriété de chaque objet. Cela est particulièrement vrai pour les forces électriques, bien que dans les exemples d'énergie potentielle que nous examinons ci-dessous, certaines parties du système soient soit si grandes (comme la Terre, par rapport à un objet à sa surface) soit si petites (comme un ressort sans masse) que les changements subis par ces parties sont négligeables lorsqu'elles sont incluses dans le système.
Types d'énergie potentielle
Pour chaque type d'interaction présent dans un système, vous pouvez étiqueter un type d'énergie potentielle correspondant. L'énergie potentielle totale du système est la somme des énergies potentielles de tous les types. (Cela découle de la propriété additive du produit scalaire dans l'expression du travail effectué.) Examinons quelques exemples spécifiques de types d'énergie potentielle abordés dans Work. Tout d'abord, nous prenons en compte chacune de ces forces lorsqu'elles agissent séparément, puis lorsque les deux agissent ensemble.
Énergie potentielle gravitationnelle près de la surface de la Terre
Le système d'intérêt comprend notre planète, la Terre, et une ou plusieurs particules proches de sa surface (ou des corps suffisamment petits pour être considérés comme des particules, par rapport à la Terre). La force gravitationnelle exercée sur chaque particule (ou corps) est juste son poids en mg près de la surface de la Terre, agissant verticalement vers le bas. Selon la troisième loi de Newton, chaque particule exerce sur Terre une force d'intensité égale mais dans la direction opposée. La deuxième loi de Newton nous indique que l'amplitude de l'accélération produite par chacune de ces forces sur Terre est divisée en mg par la masse de la Terre. Comme le rapport entre la masse d'un objet ordinaire et la masse de la Terre est très faible, le mouvement de la Terre peut être complètement négligé. Par conséquent, nous considérons ce système comme un groupe de systèmes à particules uniques, soumis à la force gravitationnelle uniforme de la Terre.
Dans Work, le travail effectué sur un corps par la force gravitationnelle uniforme de la Terre, près de sa surface, dépendait de la masse du corps, de l'accélération due à la gravité et de la différence de hauteur parcourue par le corps, comme indiqué par l'équation 7.2.4. Par définition, ce travail est le négatif de la différence d'énergie potentielle gravitationnelle, de sorte que cette différence est
\[\Delta U_{\mathrm{grav}}=-W_{\mathrm{grav}, A B}=m g\left(y_{B}-y_{A}\right) \label{8.4}.\]
Vous pouvez en déduire que la fonction d'énergie potentielle gravitationnelle, près de la surface de la Terre, est
\[U(y)=m g y+\text { const. } \label{8.5}\]
Vous pouvez choisir la valeur de la constante, comme décrit dans la discussion de l'équation \ ref {8.2} ; toutefois, pour résoudre la plupart des problèmes, la constante la plus pratique à choisir est zéro lorsque y = 0, qui est la position verticale la plus basse du problème.
Le sommet de Great Blue Hill à Milton, dans le Massachusetts, se trouve à 147 m au-dessus de sa base et a une altitude au-dessus du niveau de la mer de 195 m (Figure\(\PageIndex{2}\)). (Son nom amérindien, Massachusett, a été adopté par les colons pour avoir baptisé la Bay Colony et l'État situés à proximité de son emplacement.) Un randonneur de 75 kg monte de la base au sommet. Quelle est l'énergie potentielle gravitationnelle du système Hiker-Earth par rapport à l'énergie potentielle gravitationnelle nulle à la hauteur de base, lorsque le randonneur se trouve (a) au pied de la colline, (b) au sommet et (c) au niveau de la mer, ensuite ?
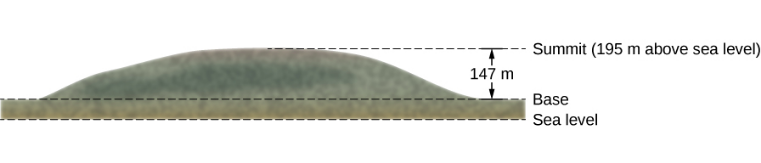
Stratégie
Nous devons d'abord choisir une origine pour l'axe y, puis déterminer la valeur de la constante qui rend l'énergie potentielle nulle à la hauteur de la base. Ensuite, nous pouvons déterminer les énergies potentielles à partir de l'équation \ ref {8.5}, en fonction de la relation entre la hauteur d'énergie potentielle nulle et la hauteur à laquelle se trouve le randonneur.
Solution
a. Choisissons l'origine de l'axe y à la hauteur de base, où nous voulons également que se trouve le zéro de l'énergie potentielle. Ce choix rend la constante égale à zéro et
\[U(\text { base })=U(0)=0 \nonumber\]
b. Au sommet, y = 147 m, donc
\[ U(\text { summit }) = U(147 \: \mathrm{m})=m g h=(75 \times 9.8 \: \mathrm{N})(147 \: \mathrm{m})=108 \: \mathrm{kJ}. \nonumber \]
c. Au niveau de la mer, y = (147 - 195) m = -48 m, donc
\[ U \text { (sea-level) }=(75 \times 9.8 \mathrm{N})(-48 \mathrm{m})=-35.3 \mathrm{kJ} .\nonumber \]
L'importance
En plus d'illustrer l'utilisation de l'équation \ ref {8.4} et de l'équation \ ref {8.5}, les valeurs de l'énergie potentielle gravitationnelle que nous avons trouvées sont raisonnables. L'énergie potentielle gravitationnelle est plus élevée au sommet qu'à la base et plus faible au niveau de la mer qu'à la base. La gravité agit aussi sur vous lorsque vous montez ! Il fait un travail négatif et pas tout à fait autant (en ampleur) que vos muscles. Mais cela fonctionne certainement. De même, vos muscles travaillent quand vous descendez, sous forme de travail négatif. Les valeurs numériques des énergies potentielles dépendent du choix du zéro de l'énergie potentielle, mais ce n'est pas le cas des différences physiques significatives d'énergie potentielle. [Notez que puisque l'équation \ ref {8.2} est une différence, les valeurs numériques ne dépendent pas de l'origine des coordonnées.]
Quelles sont les valeurs de l'énergie potentielle gravitationnelle du randonneur à la base, au sommet et au niveau de la mer, par rapport à une énergie potentielle nulle au niveau de la mer ?
Énergie potentielle élastique
Dans Work, nous avons vu que le travail effectué par un ressort parfaitement élastique, dans une dimension, ne dépend que de la constante du ressort et des carrés des déplacements depuis la position non étirée, comme indiqué dans l'équation 7.2.5. Ce travail ne porte que sur les propriétés d'une interaction de la loi de Hooke et non sur les propriétés des véritables sources et des objets qui y sont attachés. Par conséquent, nous pouvons définir la différence d'énergie potentielle élastique pour une force de ressort comme étant la valeur négative du travail effectué par la force du ressort dans cette équation, avant de considérer les systèmes qui incarnent ce type de force. Ainsi,
\[\Delta U=-W_{A B}=\frac{1}{2} k\left(x_{B}^{2}-x_{A}^{2}\right) \label{8.6} \]
où l'objet se déplace d'un point A à un point B. La fonction d'énergie potentielle correspondant à cette différence est
\[U(x)=\frac{1}{2} k x^{2}+\text { const. } \label{8.7} \]
Si la force du ressort est la seule force agissant, il est plus simple de prendre le zéro de l'énergie potentielle à x = 0, lorsque le ressort est à sa longueur libre. Ensuite, la constante est Equation \ ref {8.7} vaut zéro. (D'autres choix peuvent être plus pratiques si d'autres forces agissent.)
Un système contient un ressort parfaitement élastique, d'une longueur non étirée de 20 cm et d'une constante de ressort de 4 N/cm. a) Quelle est la quantité d'énergie potentielle élastique fournie par le ressort lorsque sa longueur est de 23 cm ? (b) Quelle énergie potentielle supplémentaire fournit-elle si sa longueur augmente à 26 cm ?
Stratégie
Lorsque le ressort est à sa longueur libre, il ne contribue en rien à l'énergie potentielle du système. Nous pouvons donc utiliser l'équation \ ref {8.7} avec la constante égale à zéro. La valeur de x est la longueur moins la longueur non étirée. Lorsque le ressort est dilaté, le déplacement du ressort ou la différence entre sa longueur détendue et sa longueur étirée doivent être utilisés pour la valeur x dans le calcul de l'énergie potentielle du ressort.
Solution
- Le déplacement du ressort est x = 23 cm − 20 cm = 3 cm, donc l'énergie potentielle apportée est U =\(\frac{1}{2}\) kx 2 =\(\frac{1}{2}\) (4 N/cm) (3 cm) 2 = 0,18 J.
- Lorsque le déplacement du ressort est x = 26 cm − 20 cm = 6 cm, l'énergie potentielle est U =\(\frac{1}{2}\) kx 2 =\(\frac{1}{2}\) (4 N/cm) (6 cm) 2 = 0,72 J, soit une augmentation de 0,54 J par rapport à la quantité en partie (a).
L'importance
Le calcul de l'énergie potentielle élastique et des différences d'énergie potentielle à partir de l'équation \ ref {8.7} implique de résoudre les énergies potentielles en fonction des longueurs données du ressort. Comme U dépend de x 2, l'énergie potentielle pour une compression (x négatif) est la même que pour une extension de même amplitude.
Lorsque la longueur du ressort de l'exemple 8.2.3 passe d'une valeur initiale de 22,0 cm à une valeur finale, l'énergie potentielle élastique qu'il fournit change de −0,0800 J. Trouvez la longueur finale.
Énergie potentielle gravitationnelle et élastique
Un système simple incarnant à la fois des types d'énergie potentielle gravitationnelle et élastique est un système masse-ressort vertical unidimensionnel. Il s'agit d'une particule massive (ou d'un bloc) suspendue à une extrémité d'un ressort sans masse parfaitement élastique, dont l'autre extrémité est fixe, comme illustré sur la figure\(\PageIndex{3}\).
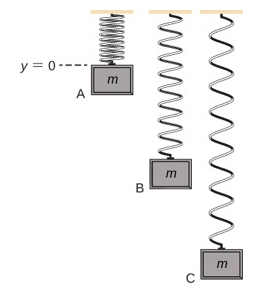
Examinons d'abord l'énergie potentielle du système. Nous devons définir la constante de la fonction d'énergie potentielle de l'équation \ ref {8.5}. Le sol est souvent un choix approprié lorsque l'énergie potentielle gravitationnelle est nulle ; cependant, dans ce cas, le point le plus élevé ou lorsque y = 0 est un endroit pratique pour une énergie potentielle gravitationnelle nulle. Notez que ce choix est arbitraire et que le problème peut être résolu correctement même si vous choisissez un autre choix.
Nous devons également définir l'énergie potentielle élastique du système et la constante correspondante, comme détaillé dans l'équation \ ref {8.7}. C'est là que le ressort n'est pas étiré, ou à la position y = 0.
Si l'on considère que l'énergie totale du système est conservée, alors l'énergie au point A est égale au point C. Le bloc est placé juste sur le ressort de sorte que son énergie cinétique initiale soit nulle. Selon la configuration du problème discuté précédemment, l'énergie potentielle gravitationnelle et l'énergie potentielle élastique sont égales à zéro. Par conséquent, l'énergie initiale du système est nulle. Lorsque le bloc arrive au point C, son énergie cinétique est nulle. Cependant, il possède désormais à la fois une énergie potentielle gravitationnelle et une énergie potentielle élastique. Par conséquent, nous pouvons résoudre la distance y que le bloc parcourt avant de s'arrêter :
\ [\ begin {aligné}
K_ {\ mathrm {A}} &+U_ {A} =K_ {C} +U_ {\ mathrm {C}} \ \
0 &=0+m g y_ {C} + \ frac {1} {2} k \ left (y_ {C} \ right) ^ {2} \ \
y_ {\ mathrm {C}} &= \ frac {-2 m g} {k}
\ end {aligné} \]

Un bloc pesant 1,2 N est suspendu à un ressort dont la constante de ressort est de 6,0 N/m, comme le montre la figure\(\PageIndex{3}\). a) Quelle est la dilatation maximale du ressort, telle qu'elle est vue au point C ? (b) Quelle est l'énergie potentielle totale au point B, à mi-chemin entre A et C ? (c) Quelle est la vitesse du bloc au point B ?
Stratégie
Dans la partie (a), nous calculons la distance y C comme indiqué dans le texte précédent. Ensuite, dans la partie (b), nous utilisons la moitié de la valeur y pour calculer l'énergie potentielle au point B à l'aide des équations Equation \ ref {8.4} et Équation \ ref {8.6}. Cette énergie doit être égale à l'énergie cinétique, équation 7.3.1, au point B puisque l'énergie initiale du système est nulle. En calculant l'énergie cinétique au point B, nous pouvons maintenant calculer la vitesse du bloc au point B.
Solution
a. Comme l'énergie totale du système est nulle au point A comme indiqué précédemment, l'expansion maximale du ressort est calculée comme suit :
\ begin {array} {l}
y_ {\ mathrm {C}} = \ frac {-2 m g} {k} \ \
y_ {\ mathrm {C}} = \ frac {-2 (1.2 \ : \ mathrm {N})} {(6.0 \ : \ mathrm {N}/\ mathrm {m})} =-0,40 \ : \ mathrm {m})} =-0,40 \ : \ mathrm {m}) {m}
\ end {tableau}
b. La position de y B est la moitié de la position à y C ou -0,20 m. L'énergie potentielle totale au point B serait donc :
\ begin {aligné}
U_ {B} &=m g y_ {B} + \ left (\ frac {1} {2} k y_ {B} \ right) ^ {2} \ \
U_ {B} & =( 1,2 \ : \ mathrm {N}) (-0,20 \ : \ mathrm {m}) + \ frac {1} {2} (6 \ : mathrm {N}/\ mathrm {m}) (-0,20 \ : \ mathrm {m}) ^ {2} \ \
U_ {B} &=-0,12 \ : \ mathrm {J}
\ end {aligné}
c. La masse du bloc est le poids divisé par la gravité.
\[m=\frac{F_{w}}{g}=\frac{1.2 \: \mathrm{N}}{9.8 \: \mathrm{m} / \mathrm{s}^{2}}=0.12 \: \mathrm{kg} \nonumber \]
L'énergie cinétique au point B est donc de 0,12 J car l'énergie totale est nulle. Par conséquent, la vitesse du bloc au point B est égale à
\ begin {tableau} {l}
K= \ frac {1} {2} m v^ {2} \ \
v= \ sqrt {\ frac {2 K} {m}} = \ sqrt {\ frac {2 (0,12 \ : \ mathrm {J})} {(0,12 \ : \ mathrm {kg})} =1,4 \ : \ mathrm {M}/\ mathrm {s}
\ end {tableau}
L'importance
Même si l'énergie potentielle due à la gravité est relative à un point zéro choisi, les solutions à ce problème seraient les mêmes si les points d'énergie zéro étaient choisis à des endroits différents.
Supposons que la masse dans l'équation \ ref {8.6} soit doublée tout en conservant les mêmes conditions. L'expansion maximale du ressort augmenterait-elle, diminuerait-elle ou resterait-elle la même ? La vitesse au point B serait-elle plus grande, plus petite ou identique à la masse initiale ?
Regardez cette simulation pour en savoir plus sur la conservation de l'énergie avec un patineur ! Construisez des pistes, des rampes et des sauts pour le patineur et observez l'énergie cinétique, l'énergie potentielle et la friction lorsqu'il se déplace. Vous pouvez également emmener le patineur sur différentes planètes ou même dans l'espace !
Un exemple de diagramme de diverses énergies est présenté dans le tableau\(\PageIndex{1}\) pour vous donner une idée des valeurs énergétiques typiques associées à certains événements. Certains d'entre eux sont calculés en utilisant l'énergie cinétique, tandis que d'autres sont calculés en utilisant des quantités trouvées sous une forme d'énergie potentielle qui n'a peut-être pas été discutée à ce stade.
| Objet/phénomène | Énergie en joules |
|---|---|
| Big Bang | 10 68 |
| Consommation énergétique mondiale annuelle | 4,0 x 10 20 |
| Grande bombe à fusion (9 mégatonnes) | 3,8 x 10 16 |
| Bombe à fission de la taille d'Hiroshima (10 kilotonnes) | 4,2 x 10 13 |
| 1 baril de pétrole brut | 5,9 x 10 9 |
| 1 tonne de TNT | 4,2 x 10 9 |
| 1 gallon d'essence | 1,2 x 10 8 |
| Apport alimentaire quotidien pour adultes (recommandé) | 1,2 x 10 7 |
| Voiture de 1000 kg à 90 km/h | 3,1 x 10 5 |
| Balle de tennis à 100 km/h | 22 |
| Moustique (10 −2 g à 0,5 m/s) | 1,3 x 10 -6 |
| Un seul électron dans un faisceau de tube de télévision | 4,0 x 10 -15 |
| De l'énergie pour briser un brin d'ADN | 10-19 |


