15.3 : Circuits AC simples
- Page ID
- 191200
À la fin de la section, vous serez en mesure de :
- Interpréter les diagrammes de phaseurs et les appliquer aux circuits à courant alternatif avec des résistances, des condensateurs et des inductances
- Définissez la réactance d'une résistance, d'un condensateur et d'une inductance pour mieux comprendre le comportement du courant dans le circuit par rapport à chacun de ces dispositifs
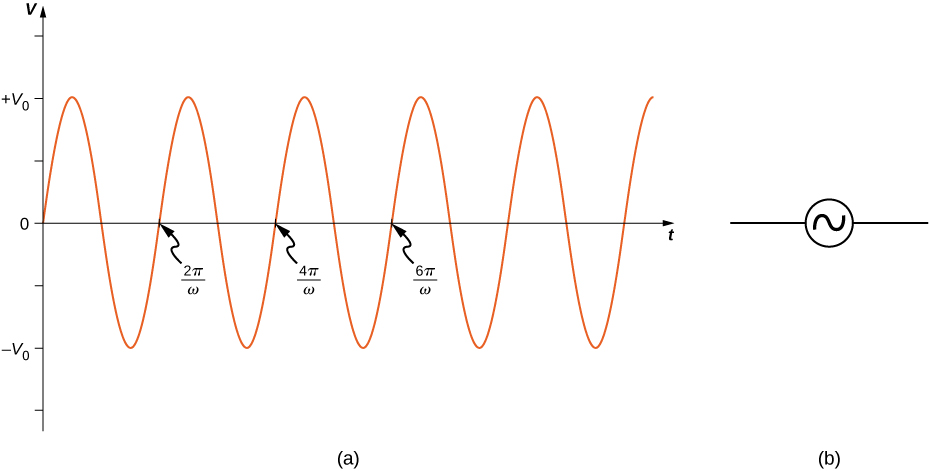
Dans cette section, nous étudions des modèles simples de sources de tension alternative connectées à trois composants du circuit : (1) une résistance, (2) un condensateur et (3) une inductance. L'énergie fournie par une source de tension alternative a une force électromotrice donnée par
\[v(t) = V_0 \, sin \, \omega t,\]
comme le montre la figure\(\PageIndex{1}\). Cette fonction sinusoïdale suppose que nous commençons à enregistrer la tension quand elle est\(v = 0 \, V\) à l'heure de\(t = 0 \, s\). Une constante de phase peut être impliquée qui déplace la fonction lorsque nous commençons à mesurer les tensions, de la même manière que la constante de phase des ondes que nous avons étudiées dans Waves. Cependant, comme nous sommes libres de choisir quand nous commençons à examiner la tension, nous pouvons ignorer cette constante de phase pour le moment. Nous pouvons mesurer cette tension aux bornes des composants du circuit en utilisant l'une des deux méthodes suivantes : (1) une approche quantitative basée sur notre connaissance des circuits, ou (2) une approche graphique expliquée dans les sections suivantes.
Résistance
Tout d'abord, considérez une résistance connectée à une source de tension alternative. D'après la règle de boucle de Kirchhoff, la tension instantanée aux bornes de la résistance de la Figure\(\PageIndex{2a}\) est
\[v_R(t) = V_0 \, sin \, \omega t\]
et le courant instantané à travers la résistance est
\[i_R(t) = \frac{v_R(t)}{R} = \frac{V_0}{R} \, sin \, \omega t = I_0 \, sin \, \omega t.\]
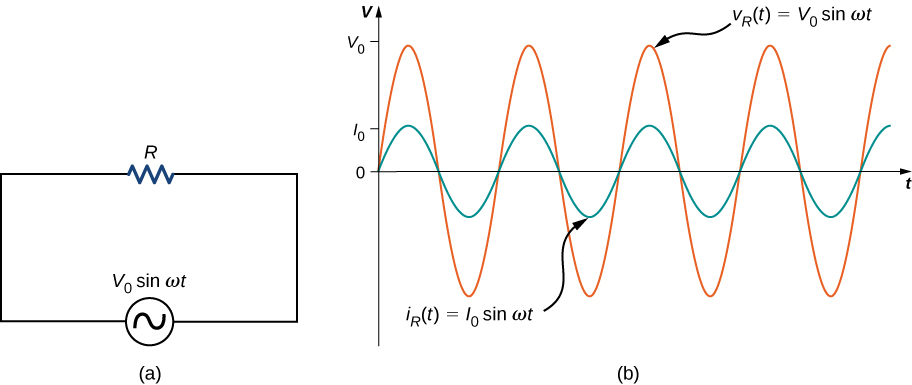
\(I_0 = V_0/R\)Voici l'amplitude du courant qui varie dans le temps. Les diagrammes de\(i_R(t)\) et\(v_R(t)\) sont présentés dans la figure\(\PageIndex{2b}\). Les deux courbes atteignent leurs maxima et leurs minima en même temps, c'est-à-dire que le courant traversant et la tension aux bornes de la résistance sont en phase.
Les représentations graphiques des relations de phase entre le courant et la tension sont souvent utiles pour l'analyse des circuits en courant alternatif. De telles représentations sont appelées diagrammes de phaseurs. Le diagramme des phaseurs pour\(i_R(t)\) est illustré sur la figure\(\PageIndex{3a}\), avec le courant sur l'axe vertical. La flèche (ou phaseur) tourne dans le sens antihoraire à une fréquence angulaire constante\(\omega\), nous la visualisons donc à un instant. Si la longueur de la flèche correspond à l'amplitude du courant\(I_0\), la projection de la flèche rotative sur l'axe vertical est\(i_R(t) = I_0 \, sin \, \omega t\), qui est le courant instantané.
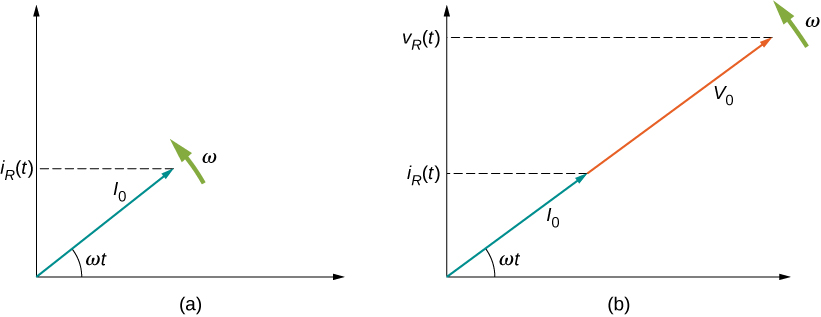
L'axe vertical sur un diagramme de phaseur peut être la tension ou le courant, selon le phaseur examiné. De plus, plusieurs grandeurs peuvent être représentées sur le même diagramme de phaseur. Par exemple, le courant\(i_R(t)\) et la tension\(v_R(t)\) sont indiqués sur le schéma de la figure\(\PageIndex{3b}\). Comme ils ont la même fréquence et sont en phase, leurs phaseurs pointent dans la même direction et tournent ensemble. Les longueurs relatives des deux phaseurs sont arbitraires car elles représentent des quantités différentes ; cependant, le rapport des longueurs des deux phaseurs peut être représenté par la résistance, puisque l'un est un phaseur de tension et l'autre est un phaseur de courant.
condensateur
Considérons maintenant un condensateur connecté à une source de tension alternative. D'après la règle de la boucle de Kirchhoff, la tension instantanée aux bornes du condensateur de la Figure\(\PageIndex{4a}\) est
\[v_C(t) = V_0 \, sin \, \omega t.\]
Rappelons que la charge d'un condensateur est donnée par\(Q = CV\). Cela est vrai à tout moment mesuré dans le cycle de tension en courant alternatif. Par conséquent, la charge instantanée sur le condensateur est
\[q(t) = Cv_C(t) = CV_0 \, sin \, \omega t.\]
Puisque le courant dans le circuit est la vitesse à laquelle la charge entre (ou sort) du condensateur,
\[i_C(t) = \frac{dq(t)}{dt} = \omega CV_0 \, cos \, \omega t = I_0 \, cos \, \omega t,\]
où\(I_0 = \omega CV_0\) est l'amplitude du courant. En utilisant la relation trigonométrique\(cos \, \omega t = sin (\omega t + \pi/2)\), nous pouvons exprimer le courant instantané comme
\[i_C(t) = I_0 \, sin \left(\omega t + \frac{\pi}{2}\right).\]
\(V_0\)En divisant par\(I_0\), nous obtenons une équation qui ressemble à la loi d'Ohm :
\[\frac{V_0}{I_0} = \frac{1}{\omega C} = X_C. \label{15.3}\]
La quantité\(X_C\) est analogue à la résistance dans un circuit à courant continu en ce sens que les deux quantités sont un rapport entre une tension et un courant. Par conséquent, ils ont la même unité, l'ohm. Gardez toutefois à l'esprit qu'un condensateur stocke et décharge l'énergie électrique, alors qu'une résistance la dissipe. La quantité\(X_C\) est connue sous le nom de réactance capacitive du condensateur, ou opposition d'un condensateur à un changement de courant. Cela dépend inversement de la fréquence de la source de courant alternatif : une fréquence élevée entraîne une faible réactance capacitive.
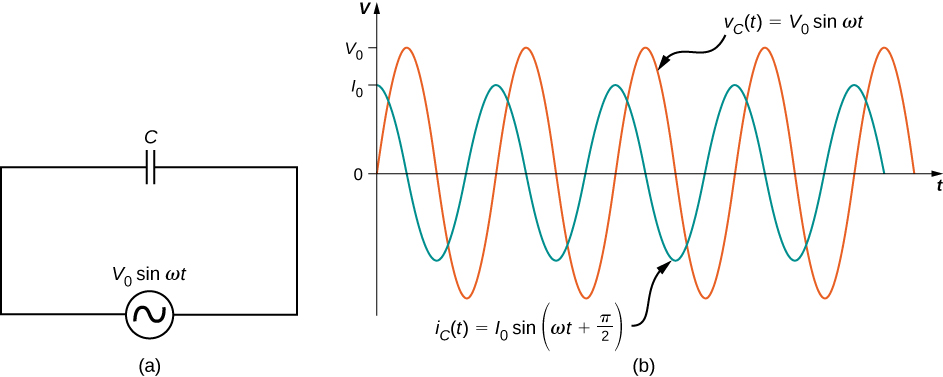
Une comparaison des expressions pour\(v_C(t)\) et\(i_C(t)\) montre qu'il existe une différence de phase de\(\pi/2\) rad entre elles. Lorsque ces deux quantités sont tracées ensemble, le courant culmine un quart de cycle (ou\(\pi/2\) rad) avant la tension, comme illustré sur la figure\(\PageIndex{4b}\). Le courant traversant un condensateur conduit la tension à travers un condensateur de\(\pi/2\) rad, soit un quart de cycle.
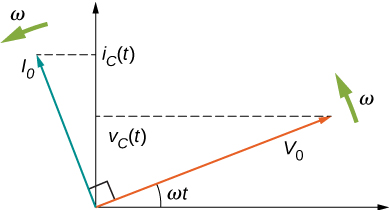
Le diagramme de phaseur correspondant est illustré sur la figure\(\PageIndex{5}\). Ici, la relation entre\(i_C(t)\) et\(v_C(t)\) est représentée par le fait que leurs phaseurs tournent à la même fréquence angulaire, le phaseur actuel étant dirigé par\(\pi/2\) rad.
À ce stade, nous avons utilisé exclusivement les valeurs de pointe du courant ou de la tension dans notre discussion, à savoir,\(I_0\) et\(V_0\). Cependant, si nous faisons la moyenne des valeurs de courant ou de tension, ces valeurs sont nulles. Par conséquent, nous utilisons souvent une deuxième convention appelée valeur quadratique moyenne, ou valeur efficace, dans les discussions sur le courant et la tension. Le RMS fonctionne à l'inverse de la terminologie. Tout d'abord, vous mettez la fonction au carré, ensuite, vous prenez la moyenne, puis vous trouvez la racine carrée. Par conséquent, les valeurs efficaces du courant et de la tension ne sont pas nulles. Les appareils et les appareils sont généralement indiqués avec des valeurs efficaces pour leur fonctionnement, plutôt que des valeurs de pointe. Nous indiquons les valeurs RMS avec un indice attaché à une majuscule (par exemple\(I_{rms}\)).
Bien qu'un condensateur soit essentiellement un circuit ouvert, un courant efficace, ou le carré moyen du courant, apparaît dans un circuit avec une tension alternative appliquée à un condensateur. Considère que
\[I_{rms} = \frac{I_0}{\sqrt{2}},\]
où\(I_0\) est le courant de pointe dans un système à courant alternatif. La tension efficace, ou le carré moyen de la tension, est
\[V_{rms} = \frac{V_0}{\sqrt{2}},\]
où\(V_0\) est la tension de pointe dans un système à courant alternatif. Le courant efficace apparaît parce que la tension inverse, charge et décharge continuellement le condensateur. Si la fréquence passe à zéro, ce qui serait une tension continue,\(X_C\) tend vers l'infini et que le courant est nul une fois le condensateur chargé. Aux très hautes fréquences, la réactance du condensateur tend à être nulle : sa réactance est négligeable et n'entrave pas le courant (il agit comme un simple fil).
Inducteur
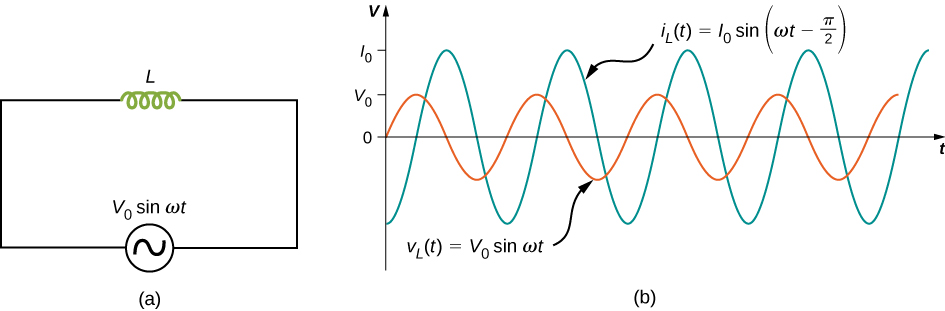
Enfin, considérons un inducteur connecté à une source de tension alternative. D'après la règle de la boucle de Kirchhoff, la tension aux bornes de l'inductance L de la figure\(\PageIndex{6a}\) est
\[v_L(t) = V_0 \, sin \, \omega t. \label{15.6}\]
La force électromotrice à travers une inductance est égale à\(\epsilon = - L(di_L/dt)\) ; cependant, la différence de potentiel aux bornes de l'inducteur est\(v_L(t) = Ldi_L(t)/dt\) la suivante : si l'on considère que la tension autour de la boucle doit être nulle, la tension obtenue par la source de courant alternatif doit se dissiper à travers l'inducteur. Par conséquent, en le connectant à la source de tension alternative, nous avons
\[\frac{di_L(t)}{dt} = \frac{V_0}{L} \, sin \, \omega t.\]
Le courant\(i_L(t)\) est trouvé en intégrant cette équation. Comme le circuit ne contient pas de source de force électromotrice constante, il n'y a pas de courant constant dans le circuit. Par conséquent, nous pouvons définir la constante d'intégration, qui représente le courant constant dans le circuit, égale à zéro, et nous avons
\[i_L(t) = - \frac{V_0}{\omega L} cos \, \omega t = \frac{V_0}{\omega L} sin \left(\omega t - \frac{\pi}{2}\right) = I_0 \, sin \left(\omega t - \frac{\pi}{2}\right), \label{15.7}\]
où\(I_0 = V_0/\omega L\). La relation entre\(V_0\) et\(I_0\) peut également être écrite sous une forme analogue à la loi d'Ohm :
\[\frac{V_0}{I_0} = \omega L = X_L. \label{15.8}\]
La quantité\(X_L\) est connue sous le nom de réactance inductive de l'inducteur, ou opposition d'un inducteur à un changement de courant ; son unité est également l'ohm. Notez que cela\(X_L\) varie directement en fonction de la fréquence de la source de courant alternatif : la haute fréquence provoque une réactance inductive élevée.
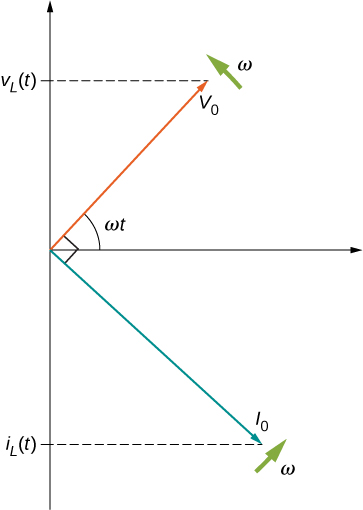
Une différence de phase de\(\pi/2\) rad se produit entre le courant traversant et la tension aux bornes de l'inducteur. À partir de l'équation \ ref {15.6} et de l'équation \ ref {15.7}, le courant traversant un inducteur est décalé par\(\pi/2\) rad par rapport à la différence de potentiel sur un inducteur, soit un quart de cycle. Le diagramme des phaseurs de ce cas est illustré sur la figure\(\PageIndex{7}\).
Une animation de l'université de New South Wales AC Circuits illustre certains des concepts abordés dans ce chapitre. Ils incluent également des diagrammes d'ondes et de phaseurs qui évoluent au fil du temps afin que vous puissiez avoir une meilleure idée de la façon dont chacun change au fil du temps.
Un générateur de courant alternatif produit une force électromotrice d'amplitude 10 V à une fréquence donnée\(f = 60 \, Hz\). Déterminez les tensions aux bornes et les courants à travers les éléments du circuit lorsque le générateur est connecté à (a) une\(100 \, \Omega\) résistance, (b) un\(10 \, \mu F\) condensateur et (c) une inductance de 15 mH.
Stratégie
La tension alternative totale sur chaque appareil est identique à la tension de la source. Nous pouvons trouver les courants en trouvant la réactance X de chaque appareil et en résolvant le courant de pointe en utilisant\(I_0 = V_0/X\).
Solution
La tension aux bornes de la source est
\[v(t) = V_0 \, sin \, \omega t = (10 \, V) sin \, 120 \pi t,\]
où\(\omega = 2\pi f = 120 \pi \, rad/s\) est la fréquence angulaire. Puisque v (t) est également la tension aux bornes de chacun des éléments, nous avons
\[v(t) = v_R(t) = v_C(t) = v_L(t) = (10 \, V) sin \, 120 \pi t.\]
a. Lorsque\(R = 100 \, \Omega\) l'amplitude du courant traversant la résistance est
\[I_0 = V_0/R = 10 \, V/100 \, \Omega = 0.10 \, A,\]donc
\[i_R(t) = (0.10 \, A) sin \, 120 \pi t.\]
b. À partir de l'équation \ ref {15.3}, la réactance capacitive est
\[X_C = \frac{1}{\omega C} = \frac{1}{(120 \pi \, rad/s)(10 \times 10^{-6}F)} = 265 \, \Omega,\]
donc la valeur maximale du courant est
\[I_0 = \frac{V_0}{X_C} = \frac{10 \, V}{265 \, \Omega} = 3.8 \times 10^{-2} \, A\]
et le courant instantané est donné par
\[i_C(t) = (3.8 \times 10^{-2} \, A) \, sin \, \left(120 \pi t + \frac{\pi}{2}\right).\]
c. À partir de l'équation \ ref {15.8}, la réactance inductive est
\[ X_L = \omega L = (120 \pi \, rad/s)(15 \times 10^{-3} H) = 5.7 \, \Omega.\]
Le courant maximal est donc
\[I_0 = \frac{10 \, V}{5.7 \, \Omega} = 1.8 \, A\]
et le courant instantané est
\[i_L(t) = (1.8 \, A) \, sin \left(120 \pi t - \frac{\pi}{2}\right).\]
L'importance
Bien que la tension aux bornes de chaque appareil soit la même, le courant de pointe a des valeurs différentes, en fonction de la réactance. La réactance de chaque dispositif dépend des valeurs de résistance, de capacité ou d'inductance.
Répétez\(\PageIndex{1}\) l'exemple pour une source de courant alternatif d'amplitude 20 V et de fréquence 100 Hz.
- Réponse
-
un\((20 \, V) \, sin \, 200 \pi t\),\((0.20 \, A) \, sin \, 200 \pi t\) ;
b.\((20 \, V) \, sin \, 200 \pi t\),\((0.13 \, A) \, sin \, (200\pi t + \pi /2)\) ;
c.\((20 \, V) \, sin \, 200 \pi t\),\((2.1 \, A) \, sin \, (200 \pi t - \pi/2)\)


