7.2 : Énergie potentielle électrique
- Page ID
- 191252
À la fin de cette section, vous serez en mesure de :
- Définir le travail effectué par une force électrique
- Définir l'énergie potentielle électrique
- Appliquez du travail et de l'énergie potentielle aux systèmes alimentés par des charges électriques
Lorsqu'une charge positive libre q est accélérée par un champ électrique, elle reçoit de l'énergie cinétique (Figure\(\PageIndex{1}\)). Le processus est analogue à celui d'un objet accéléré par un champ gravitationnel, comme si la charge descendait une colline électrique où son énergie potentielle électrique est convertie en énergie cinétique, bien que les sources des forces soient bien entendu très différentes. Explorons le travail effectué sur une charge q par le champ électrique au cours de ce processus, afin de développer une définition de l'énergie potentielle électrique.
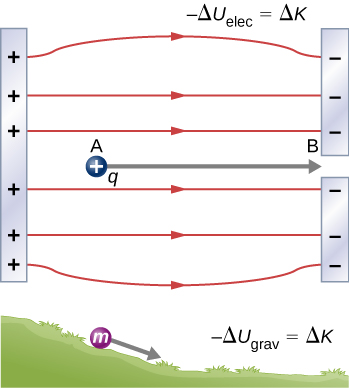
La force électrostatique ou force de Coulomb est conservatrice, ce qui signifie que le travail effectué sur q est indépendant du chemin emprunté, comme nous le démontrerons plus loin. C'est exactement analogue à la force gravitationnelle. Lorsqu'une force est conservatrice, il est possible de définir une énergie potentielle associée à la force. Il est généralement plus facile de travailler avec l'énergie potentielle (car elle ne dépend que de la position) que de calculer le travail directement.
Pour le montrer de manière explicite, considérez une charge électrique\(+q\) fixée à l'origine et déplacez une autre charge\(+Q\) vers q de telle sorte que, à chaque instant, la force appliquée équilibre\(\vec{F}\) exactement la force électrique\(\vec{F}_e\) sur Q (Figure\(\PageIndex{2}\)). Le travail effectué par la force appliquée\(\vec{F}\) sur la charge Q modifie l'énergie potentielle de Q. Nous appelons cette énergie potentielle l'énergie potentielle électrique de Q.
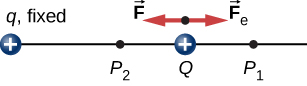
Le travail\(W_{12}\) effectué par la force appliquée\(\vec{F}\) lorsque la particule se déplace de\(P_1\) à\(P_2\) peut être calculé par
\[W_{12} = \int_{P_1}^{P_2} \vec{F} \cdot d\vec{l}.\]
Puisque la force appliquée\(\vec{F}\) équilibre la force électrique\(\vec{F}_e\) sur Q, les deux forces ont la même amplitude et des directions opposées. Par conséquent, la force appliquée est
\[\vec{F} = -\vec{F}_e = - \dfrac{kqQ}{r^2} \hat{r},\]
où nous avons défini le positif comme pointant à l'opposé de l'origine et r est la distance par rapport à l'origine. Les directions du déplacement et de la force appliquée dans le système de la figure\(\PageIndex{2}\) sont parallèles, de sorte que le travail effectué sur le système est positif.
Nous utilisons la lettre U pour désigner l'énergie potentielle électrique, qui a des unités de joules (J). Lorsqu'une force conservatrice effectue un travail négatif, le système gagne de l'énergie potentielle. Lorsqu'une force conservatrice fait un travail positif, le système perd de l'énergie potentielle,\(\Delta U = - W\). Dans le système de la figure\(\PageIndex{3}\), la force de Coulomb agit dans la direction opposée au déplacement ; par conséquent, le travail est négatif. Cependant, nous avons augmenté l'énergie potentielle dans le système à deux charges.
Une\(+3.0-nC\) charge Q est initialement au repos à une distance de 10 cm (\(r_1\)) d'une\(+5.0-nC\) charge q fixée à l'origine (Figure\(\PageIndex{3}\)). Naturellement, la force de Coulomb accélère Q en l'éloignant de q, pour finalement atteindre 15 cm (\(r_2\)).
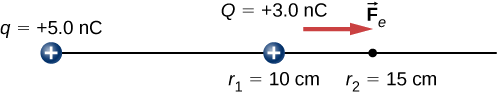
- Quel est le travail effectué par le champ électrique entre\(r_1\) et\(r_2\) ?
- Quelle est la quantité d'énergie cinétique de Q\(r_2\) ?
Stratégie
Calculez le travail avec la définition habituelle. Puisque Q est parti du repos, c'est la même chose que l'énergie cinétique.
Solution
En intégrant la force à la distance, nous obtenons
\[\begin{align} W_{12} &= \int_{r_1}^{r_2} \vec{F} \cdot d\vec{r} \nonumber \\[4pt] &= \int_{r_1}^{r_2} \dfrac{kqQ}{r^2}dr \nonumber \\[4pt] &= \left. - \dfrac{kqQ}{r} \right|_{r_1}^{r_2} \nonumber \\[4pt] &= kqQ \left[\dfrac{-1}{r_2} + \dfrac{1}{r_1}\right] \nonumber \\[4pt] &= (8.99 \times 10^9 \, Nm^2/C^2)(5.0 \times 10^{-9} C)(3.0 \times 10^{-9} C) \left[ \dfrac{-1}{0.15 \, m} + \dfrac{1}{0.10 \, m}\right] \nonumber \\[4pt] &= 4.5 \times 10^{-7} \, J. \nonumber \end{align} \nonumber\]
C'est également la valeur de l'énergie cinétique à\(r_2\).
L'importance
La charge Q était initialement au repos ; le champ électrique de q a fonctionné sur Q, donc maintenant Q a une énergie cinétique égale au travail effectué par le champ électrique.
Si Q a une masse de\(4.00 \, \mu g\), quelle est la vitesse de Q à\(r_2\) ?
Solution
\(K = \frac{1}{2}mv^2\),\(v = \sqrt{2\frac{K}{m}} = \sqrt{2\frac{4.5 \times 10^{-7}J}{4.00 \times 10^{-9}kg}} = 15 \, m/s.\)
Dans cet exemple, le travail W effectué pour accélérer une charge positive depuis le repos est positif et résulte d'une perte de U, ou d'un négatif\(\Delta U\). Une valeur pour U peut être trouvée à n'importe quel point en prenant un point comme référence et en calculant le travail nécessaire pour déplacer une charge vers l'autre point.
Le travail W effectué pour accélérer une charge positive depuis le repos est positif et résulte d'une perte de U, ou d'un négatif\(\Delta U\). Mathématiquement,
\[W = - \Delta U. \label{7.1}\]
L'énergie potentielle gravitationnelle et l'énergie potentielle électrique sont tout à fait analogues. L'énergie potentielle représente le travail effectué par une force conservatrice et donne des informations supplémentaires sur l'énergie et la transformation de l'énergie sans qu'il soit nécessaire de traiter directement la force. Il est beaucoup plus courant, par exemple, d'utiliser le concept d'énergie potentielle électrique que de traiter directement la force de Coulomb dans des applications réelles.
En coordonnées polaires avec q à l'origine et Q situé à r, le vecteur de l'élément de déplacement est\(d\vec{l} = \hat{r} dr\) et donc l'œuvre devient
\[\begin{align} W_{12} &= kqQ \int_{r_1}^{r_2} \dfrac{1}{r^2} \hat{r} \cdot \hat{r} dr \nonumber \\[4pt] &= \underbrace{kqQ \dfrac{1}{r_2}}_{final \, point} - \underbrace{kqQ \dfrac{1}{r_1}}_{initial \,point}. \end{align}\]
Notez que ce résultat ne dépend que des points de terminaison et qu'il est par ailleurs indépendant du chemin emprunté. Pour approfondir cette question, comparez le chemin\(P_1\)\(P_2\) à celui de\(P_1 P_3 P_4 P_2\) la figure\(\PageIndex{4}\).
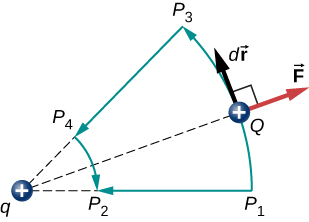
Les segments\(P_1P_3\) et\(P_4P_2\) sont des arcs de cercles centrés sur q. Puisque la force sur Q pointe vers ou loin de q, aucune action n'est réalisée par une force équilibrant la force électrique, car elle est perpendiculaire au déplacement le long de ces arcs. Par conséquent, le seul travail effectué est un long segment\(P_3P_4\) identique à\(P_1P_2\).
L'une des implications de ce calcul de travail est que si nous devions contourner le chemin\(P_1P_3P_4P_2P_1\), le réseau serait nul (Figure\(\PageIndex{5}\)). Rappelons que c'est ainsi que nous déterminons si une force est conservatrice ou non. Par conséquent, étant donné que la force électrique est liée au champ électrique par\(\vec{F} = g\vec{E}\), le champ électrique est lui-même conservateur. C'est-à-dire
\[\oint \vec{E} \cdot d\vec{l} = 0.\]
Notez que Q est une constante.

Une autre implication est que nous pouvons définir une énergie potentielle électrique. Rappelons que le travail effectué par une force conservatrice s'exprime également comme la différence d'énergie potentielle correspondant à cette force. Par conséquent, l'œuvre\(W_{ref}\) visant à faire passer une charge d'un point de référence à un point d'intérêt peut être écrite comme
\[W_{ref} = \int_{r_{ref}}^r \vec{F} \cdot d\vec{l}\]
et, par l'équation \ ref {7.1}, la différence d'énergie potentielle (\(U_2 - U_1\)) de la charge d'essai Q entre les deux points est
\[\Delta U = - \int_{r_{ref}}^r \vec{F} \cdot d\vec{l}.\]
Par conséquent, nous pouvons écrire une expression générale pour l'énergie potentielle de deux charges ponctuelles (en coordonnées sphériques) :
\[\Delta U = - \int_{r_{ref}}^r \dfrac{kqQ}{r^2}dr = -\left[-\dfrac{kqQ}{r}\right]_{r_{ref}}^r = kqQ\left[ \dfrac{1}{r} - \dfrac{1}{r_{ref}}\right].\]
Nous pouvons considérer le second terme comme un niveau de référence constant arbitraire, qui sert de référence zéro :
\[U(r) = k\dfrac{qQ}{r} - U_{ref}.\]
Un choix de référence pratique qui repose sur notre bon sens est que lorsque les deux accusations sont infiniment éloignées, il n'y a aucune interaction entre elles. (Souvenez-vous de la discussion sur l'énergie potentielle de référence dans Énergie potentielle et conservation de l'énergie.) Si l'énergie potentielle de cet état est nulle, le terme est supprimé\(U_{ref}\) de l'équation (comme lorsque nous disons que le sol est une énergie potentielle nulle dans un problème d'énergie potentielle gravitationnelle), et l'énergie potentielle de Q lorsqu'il est séparé de q par une distance r prend la forme
\[\underbrace{U(r) = k\dfrac{qQ}{r}}_{zero \, reference \, at \, r = \infty}.\]
Cette formule est symétrique par rapport à\(q\) et\(Q\), il est donc préférable de la décrire comme l'énergie potentielle du système à deux charges.
Une\(+3.0-nC\) charge Q est initialement au repos à une distance de 10 cm\((r_1)\) d'une\(+5.0-nC\) charge q fixée à l'origine (Figure\(\PageIndex{6}\)). Naturellement, la force de Coulomb accélère Q en l'éloignant de q, pour finalement atteindre 15 cm\((r_2)\).
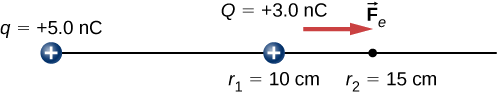
Quel est le changement de l'énergie potentielle du système à deux charges de\(r_1\) à\(r_2\) ?
Stratégie
Calculez l'énergie potentielle avec la définition donnée ci-dessus :
\(\Delta U_{12} = -\int_{r_1}^{r_2} \vec{F} \cdot d\vec{r}\). Puisque Q est parti du repos, c'est la même chose que l'énergie cinétique.
Solution
Nous avons
\[\begin{align} \Delta U_{12} &= - \int_{r_1}^{r_2} \vec{F} \cdot d\vec{r} \nonumber \\[4pt] &= - \int_{r_1}^{r_2} \dfrac{kqQ}{r^2}dr \nonumber \\[4pt] &= - \left[ - \dfrac{kqQ}{r}\right]_{r_1}^{r_2} \nonumber \\[4pt] &=kqQ \left[ \dfrac{1}{r_2} - \dfrac{1}{r_1} \right] \nonumber \\[4pt] &= (8.99 \times 10^9 \, Nm^2/C^2)(5.0 \times 10^{-9} C)(3.0 \times 10^{-9} C) \left[ \dfrac{1}{0.15 \, m} - \dfrac{1}{0.10 \, m}\right] \nonumber \\[4pt] &= - 4.5 \times 10^{-7} \, J. \end{align} \]
L'importance
La variation de l'énergie potentielle est négative, comme prévu, et égale en amplitude à la variation de l'énergie cinétique dans ce système. Souvenez-vous de l'exemple\(\PageIndex{1}\) que le changement d'énergie cinétique était positif.
Quelle est l'énergie potentielle de Q par rapport à la référence zéro à l'infini at\(r_2\) dans l'exemple ci-dessus ?
Solution
Il a une énergie cinétique d'\(4.5 \times 10^{-7} \, J\)au point\(r_2\) et une énergie potentielle de\(9.0 \times 10^{-7} \, J\), ce qui signifie que lorsque Q approche de l'infini, son énergie cinétique totalise trois fois l'énergie cinétique à\(r_2\), puisque toute l'énergie potentielle est convertie en cinétique.
Selon la loi de Coulomb, les forces dues à de multiples charges sur une charge d'essai se\(Q\) superposent ; elles peuvent être calculées individuellement puis additionnées. Cela implique que les intégrales de travail et donc les énergies potentielles qui en résultent présentent le même comportement. Pour le démontrer, nous prenons un exemple d'assemblage d'un système de quatre charges.
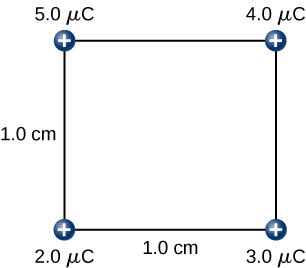
Déterminez la quantité de travail qu'un agent externe doit effectuer pour assembler quatre charges\(+2.0-\mu C\)\(+3.0-\mu C\),\(+4.0-\mu C\) et\(+5.0-\mu C\) aux sommets d'un carré de 1,0 cm de côté, en commençant chaque charge à l'infini (Figure\(\PageIndex{7}\)).
Stratégie
Nous introduisons les charges une par une, en leur donnant des points de départ infinis et en calculant le travail nécessaire pour les amener de l'infini à leur emplacement final. Nous faisons cela dans l'ordre d'augmentation de la charge.
Solution
Étape 1 Amenez d'abord la\(+2.0-\mu C\) charge à l'origine. Comme il n'y a pas encore d'autres charges à une distance finie de cette charge, aucun travail n'est fait pour la ramener de l'infini,
\[W_1 = 0.\]
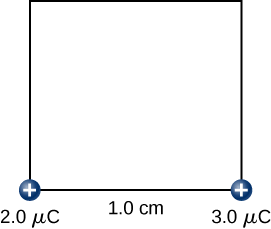
Étape 2 Tout en maintenant la\(+2.0-\mu C\) charge fixe à l'origine,\(+3.0-\mu C\) ramenez-la à\((x,y,z) = (1.0 \, cm, \, 0, \, 0)\) (Figure\(\PageIndex{8}\)). Maintenant, la force appliquée doit aller à l'encontre de la force exercée par la\(+2.0-\mu C\) charge fixée à l'origine. Le travail effectué est égal à la variation de l'énergie potentielle de la\(+3.0-\mu C\) charge :
\[\begin{align} W_2 &= k\dfrac{q_1q_2}{r{12}} \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right) \dfrac{(2.0 \times 10^{-6} C)(3.0 \times 10^{-6}C)}{1.0 \times 10^{-2} m} \nonumber \\[4pt] &= 5.4 \, J.\nonumber \end{align} \nonumber\]
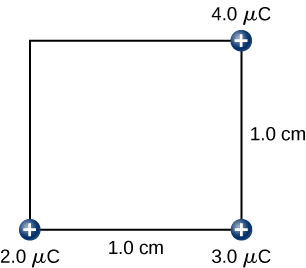
Étape 3 Tout en gardant les charges\(+2.0-\mu C\) et en les\(+3.0-\mu C\) fixant à leur place,\(+4.0-\mu C\) amenez la charge à\((x,y,z) = (1.0 \, cm, \, 1.0 \, cm, \, 0)\) (Figure)\(\PageIndex{9}\). Le travail effectué à cette étape est
\[\begin{align} W_3 &= k\dfrac{q_1q_3}{r_{13}} + k \dfrac{q_2q_3}{r_{23}} \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right) \left[ \dfrac{(2.0 \times 10^{-6}C)(4.0 \times 10^{-6}C)}{\sqrt{2} \times 10^{-2}m} + \dfrac{(3.0 \times 10^{-6} C)(4.0 \times 10^{-6}C)}{1.0 \times 10^{-2} m}\right] \nonumber \\[4pt] &= 15.9 \, J. \nonumber \end{align} \nonumber\]
Étape 4. Enfin, tout en gardant les trois premières charges à leur place, ramenez la\(+5.0-\mu C\) charge à\((x,y,z) = (0, \, 1.0 \, cm, \, 0)\) (Figure\(\PageIndex{10}\)). Le travail effectué ici est
\[\begin{align} W_4 &= kq_4 \left[ \dfrac{q_1}{r_{14}} + \dfrac{q_2}{r_{24}} + \dfrac{q_3}{r_{34}}\right], \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right)(5.0 \times 10^{-6}C) \left[ \dfrac{(2.0 \times 10^{-6}C)}{1.0 \times 10^{-2}m} + \dfrac{(3.0 \times 10^{-6} C)} {\sqrt{2} \times 10^{-2} m} + \dfrac{(4.0 \times 10^{-6}C)}{1.0 \times 10^{-2}m} \right] \nonumber \\[4pt] &= 36.5 \, J. \nonumber \end{align} \nonumber\]

Ainsi, le travail total effectué par la force appliquée pour assembler les quatre charges est égal à la somme du travail effectué pour amener chaque charge de l'infini à sa position finale :
\[\begin{align} W_T &= W_1 + W_2 + W_3 + W_4 \nonumber \\[4pt] &= 0 + 5.4 \, J + 15.9 \, J + 36.5 \, J \nonumber \\[4pt] &= 57.8 \, J. \nonumber \end{align} \nonumber\]
L'importance
Le travail sur chaque charge dépend uniquement de ses interactions par paires avec les autres charges. Aucune interaction plus complexe n'a besoin d'être envisagée ; le travail sur la troisième charge ne dépend que de son interaction avec les première et deuxième charges, l'interaction entre la première et la deuxième charge n'affecte pas la troisième.
L'énergie potentielle électrique de deux charges ponctuelles est-elle positive ou négative si les charges sont du même signe ? Des signes opposés ? Quel est le lien entre cela et le travail nécessaire pour rapprocher les charges de l'infini ?
Solution
positif, négatif, et ces quantités sont les mêmes que le travail que vous devriez effectuer pour faire entrer les charges à l'infini
Notez que l'énergie potentielle électrique est positive si les deux charges sont du même type, positive ou négative, et négative si les deux charges sont de types opposés. Cela a du sens si vous pensez à la variation de l'énergie potentielle lorsque vous rapprochez les deux charges ou\(\Delta U\) que vous les éloignez. Selon les types de frais relatifs, vous devrez peut-être travailler sur le système ou le système fonctionnera sur vous, c'est-à-dire que votre travail est positif ou négatif. Si vous devez faire un travail positif sur le système (en fait rapprocher les charges), l'énergie du système devrait augmenter. Si vous rapprochez deux charges positives ou deux charges négatives, vous devez effectuer un travail positif sur le système, ce qui augmente leur énergie potentielle. Comme l'énergie potentielle est proportionnelle à 1/ r, l'énergie potentielle augmente lorsque r descend entre deux charges positives ou deux charges négatives.
Par contre, si vous vous rapprochez d'une charge positive et d'une charge négative, vous devez effectuer un travail négatif sur le système (les charges vous attirent), ce qui signifie que vous retirez de l'énergie du système. Cela réduit l'énergie potentielle. Comme l'énergie potentielle est négative dans le cas d'une paire de charges positive et négative, l'augmentation de 1/ r rend l'énergie potentielle plus négative, ce qui équivaut à une réduction de l'énergie potentielle.
Le résultat de l'exemple\(\PageIndex{2}\) peut être étendu à des systèmes avec n'importe quel nombre de charges arbitraire. Dans ce cas, il est plus pratique d'écrire la formule sous la forme
\[W_{12 . . . N} = \dfrac{k}{2} \sum_i^N \sum_j^N \dfrac{q_iq_j}{r_{ij}} \, for \, i \neq j.\]
Le facteur 1/2 permet d'ajouter deux fois chaque paire de charges.


