2.2 : Modèle moléculaire d'un gaz idéal
- Page ID
- 191183
À la fin de cette section, vous serez en mesure de :
- Appliquez la loi des gaz idéaux à des situations impliquant la pression, le volume, la température et le nombre de molécules d'un gaz
- Utiliser l'unité des moles par rapport au nombre de molécules et aux masses moléculaires et macroscopiques
- Expliquer la loi des gaz idéaux en termes de moles plutôt que de nombre de molécules
- Appliquer la loi de Van der Waals sur les gaz aux situations où la loi sur les gaz idéale est inadéquate
Dans cette section, nous explorons le comportement thermique des gaz. Notre mot « gaz » vient du mot flamand qui signifie « chaos », utilisé pour la première fois pour désigner les vapeurs par le chimiste du XVIIe siècle J. B. van Helmont. Le terme était plus approprié qu'il ne le pensait, car les gaz sont constitués de molécules qui se déplacent et entrent en collision les unes avec les autres de manière aléatoire. Ce caractère aléatoire simplifie la connexion entre les domaines microscopique et macroscopique pour les gaz que pour les liquides ou les solides.
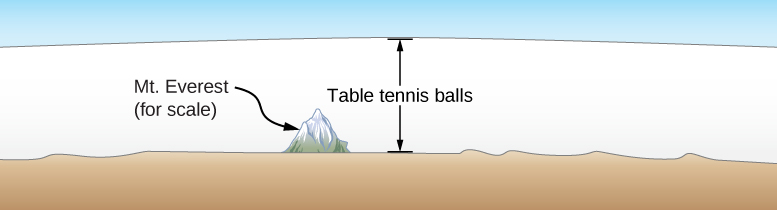
En quoi les gaz sont-ils différents des solides et des liquides ? Dans des conditions normales, comme celles de l'air qui nous entoure, la différence est que les molécules de gaz sont beaucoup plus éloignées que celles des solides et des liquides. Comme les distances typiques entre les molécules sont grandes par rapport à la taille d'une molécule, comme l'illustre la figure\(\PageIndex{1}\), les forces entre elles sont considérées comme négligeables, sauf lorsqu'elles entrent en contact les unes avec les autres lors de collisions. De plus, à des températures bien supérieures à la température d'ébullition, le mouvement des molécules est rapide et les gaz se dilatent rapidement pour occuper tout le volume accessible. En revanche, dans les liquides et les solides, les molécules sont plus proches les unes des autres, et le comportement des molécules dans les liquides et les solides est fortement limité par les interactions des molécules entre elles. Les propriétés macroscopiques de ces substances dépendent fortement des forces entre les molécules et, comme de nombreuses molécules interagissent, les « problèmes impliquant plusieurs corps » qui en résultent peuvent être extrêmement compliqués (voir la section sur la physique de la matière condensée).
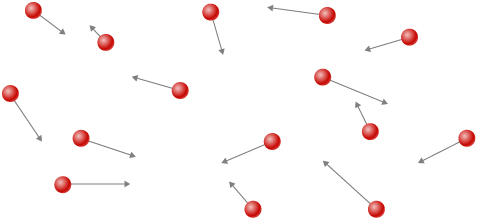
Les lois sur le gaz
Dans le chapitre précédent, nous avons vu l'une des conséquences du grand espacement intermoléculaire des gaz : les gaz sont facilement comprimés. Le tableau 1.4.1 montre que les gaz ont des coefficients de dilatation volumique plus élevés que les solides ou les liquides. Ces coefficients élevés signifient que les gaz se dilatent et se contractent très rapidement avec les changements de température. Nous avons également vu (dans la section sur la dilatation thermique) que la plupart des gaz se dilatent à la même vitesse ou ont le même coefficient de dilatation volumique\(\beta\). Cela soulève la question suivante : pourquoi tous les gaz agissent-ils presque de la même manière, alors que les différents liquides et solides ont des taux de dilatation très variables ?
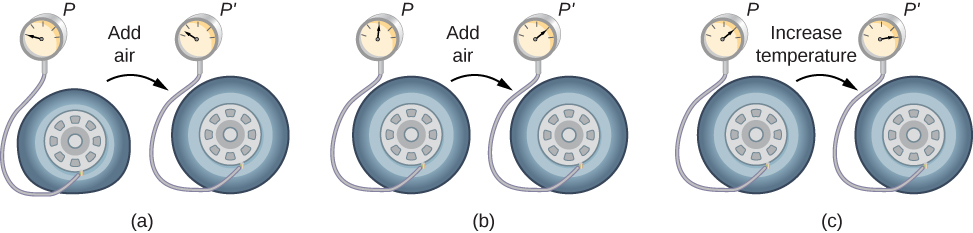
Pour étudier la relation entre la pression, la température et le volume d'un gaz, réfléchissez à ce qui se passe lorsque vous pompez de l'air dans un pneu de voiture dégonflé. Le volume du pneu augmente d'abord en proportion directe de la quantité d'air injectée, sans trop augmenter la pression du pneu. Une fois que le pneu a presque atteint sa taille maximale, les parois du pneu limitent son expansion volumique. Si nous continuons à pomper de l'air dans le pneu, la pression augmente. Lorsque la voiture roule et que les pneus fléchissent, leur température augmente et, par conséquent, la pression augmente encore (Figure\(\PageIndex{2}\)).
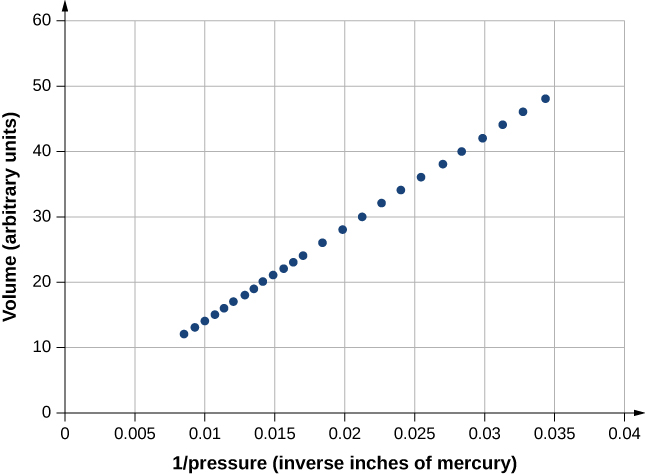
La figure\(\PageIndex{3}\) montre des données issues des expériences de Robert Boyle (1627-1691), illustrant ce que l'on appelle aujourd'hui la loi de Boyle : à température et nombre de molécules constants, la pression absolue d'un gaz et son volume sont inversement proportionnels. (Souvenez-vous de la section sur la mécanique des fluides que la pression absolue est la pression réelle et que la pression manométrique est la pression absolue moins la pression ambiante, généralement la pression atmosphérique.) Le graphique de la figure\(\PageIndex{3}\) montre cette relation sous la forme d'une proportionnalité inverse du volume à la pression.
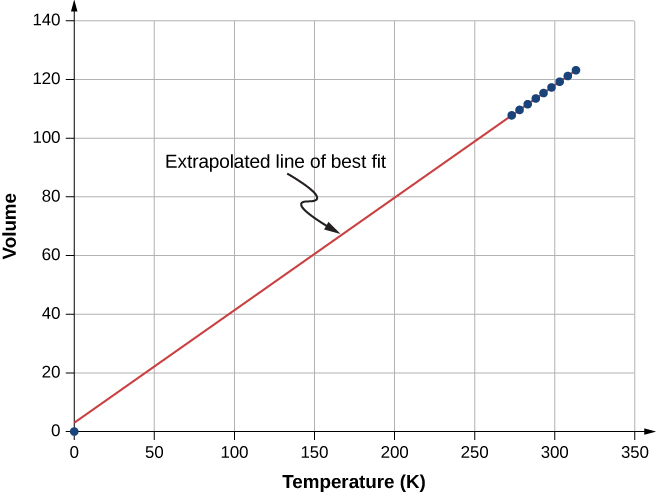
La figure\(\PageIndex{4}\) montre des données expérimentales illustrant ce que l'on appelle la loi de Charles, d'après Jacques Charles (1746—1823). La loi de Charles stipule qu'à pression et à nombre de molécules constants, le volume d'un gaz est proportionnel à sa température absolue.
La loi d'Amonton ou de Gay-Lussac est similaire, selon laquelle, à volume et nombre de molécules constants, la pression est proportionnelle à la température. Cette loi est à la base du thermomètre à gaz à volume constant, discuté dans le chapitre précédent. (L'histoire de ces lois et le crédit qui leur est attribué sont plus compliqués que ce qui peut être discuté ici.)
On sait expérimentalement que pour les gaz à faible densité (de sorte que leurs molécules occupent une fraction négligeable du volume total) et à des températures bien supérieures au point d'ébullition, ces proportionnalités sont bien approximatives. Comme on pouvait s'y attendre, les autres quantités étant maintenues constantes, la pression ou le volume sont proportionnels au nombre de molécules. Plus surprenant encore, lorsque les proportionnalités sont combinées en une seule équation, la constante de proportionnalité est indépendante de la composition du gaz. L'équation qui en résulte pour tous les gaz s'applique à la limite de faible densité et de haute température ; elle est la même pour l'oxygène que pour l'hélium ou l'hexafluorure d'uranium. Un gaz à cette limite est appelé gaz idéal ; il obéit à la loi du gaz idéal, également appelée équation d'état d'un gaz idéal.
La loi des gaz idéaux indique que,\[pV = Nk_BT,\] où p est la pression absolue d'un gaz, V est le volume qu'il occupe, N est le nombre de molécules dans le gaz et T est sa température absolue.
La constante\(k_B\) est appelée constante de Boltzmann en l'honneur du physicien autrichien Ludwig Boltzmann (1844—1906) et a pour valeur
\[k_B = 1.38 \times 10^{-23} \, J/K.\]
La loi des gaz idéaux décrit le comportement de tout gaz réel lorsque sa densité est suffisamment faible ou sa température suffisamment élevée pour qu'il soit loin de la liquéfaction. Cela englobe de nombreuses situations pratiques. Dans la section suivante, nous verrons pourquoi il est indépendant du type de gaz.
Dans de nombreuses situations, la loi idéale des gaz est appliquée à un échantillon de gaz contenant un nombre constant de molécules ; par exemple, le gaz peut se trouver dans un récipient scellé. Si N est constant, la résolution de N indique que pV/T est constant. Nous pouvons écrire ce fait sous une forme pratique :
\[\dfrac{p_1V_1}{T_1} = \dfrac{p_2V_2}{T_2},\]
où les indices 1 et 2 se réfèrent à deux états quelconques du gaz à des moments différents. Encore une fois, la température doit être exprimée en kelvins et la pression doit être la pression absolue, qui est la somme de la pression manométrique et de la pression atmosphérique.
Supposons que votre pneu de vélo soit complètement gonflé, avec une pression absolue de\(7.00 \times 10^5 \, Pa\) (une pression manométrique légèrement inférieure à\(90.0 \, lb/in^2\).) à une température de\(18.0^oC\). Quelle est la pression une fois que sa température a augmenté par une chaude journée ?\(35.0^oC\) Supposons qu'il n'y ait pas de fuite ou de changement de volume appréciable.
Stratégie
La pression dans le pneu ne change qu'à cause des changements de température. Nous connaissons la pression initiale\(p_0 = 7.00 \times 10^5 \, Pa\), la température\(T_0 = 18.0^oC\) initiale et la température finale\(T_f = 35.0^oC\). Nous devons trouver la pression finale\(p_f\). Comme le nombre de molécules est constant, nous pouvons utiliser l'équation
\[\dfrac{p_fV_f}{T_f} = \dfrac{p_0V_0}{T_0}.\]
Puisque le volume est constant,\(V_f\) qu'ils\(V_0\) sont identiques et qu'ils se divisent. Par conséquent,
\[\dfrac{p_f}{T_f} = \dfrac{p_0}{T_0}.\]
Nous pouvons ensuite réorganiser cela pour résoudre les problèmes\(p_f\) suivants :
\[p_f = p_0 \dfrac{T_f}{T_0},\]
où la température doit être exprimée en kelvins.
Solution
- Convertir les températures de degrés Celsius en kelvins\[T_0 = (18.0 + 273)K = 291 \, K,\]\[T_f = (35.0 + 273)K = 308 \, K.\]
- Remplacez les valeurs connues dans l'équation,\[p_f = p_0\dfrac{T_f}{T_0} = 7.00 \times 10^5 \, Pa \left(\dfrac{308 \, K}{291 \, K}\right) = 7.41 \times 10^5 \, Pa.\]
L'importance
La température finale est à peu près\(6\%\) supérieure à la température d'origine, de sorte que la pression finale est également à peu près\(6\%\) supérieure. Notez que la pression absolue (voir Mécanique des fluides) et la température absolue (voir Température et chaleur) doivent être utilisées dans la loi des gaz idéaux.
Combien de molécules se trouvent dans un objet typique, comme de l'essence dans un pneu ou de l'eau dans un verre ? Ce calcul peut nous donner une idée de la taille typique de N. Calculons le nombre de molécules présentes dans l'air qu'un jeune adulte en bonne santé inhale en une seule respiration, avec un volume de 500 ml, à une température et une pression standard (STP), définies comme\(0^oC\) la pression atmosphérique. (Notre jeune adulte est apparemment dehors en hiver.)
Stratégie
Comme la pression, le volume et la température sont tous spécifiés, nous pouvons utiliser la loi des gaz idéale, \ (pV = k_BT \}, pour trouver N.
Solution
- Identifiez les éléments connus. \[T = 0^oC = 273 \, K, \, p = 1.01 \times 10^5 \, Pa, \, V = 500 \, mL = 5 \times 10^{-4} \, m^3, \, k_B = 1.38 \times 10^{-23} \, J/K\]
- Substituez les valeurs connues dans l'équation et résolvez pour N. \[N = \dfrac{pV}{k_BT} = \dfrac{(1.01 \times 10^5 \, Pa)(5 \times 10^{-4} \, m^3)}{(1.38 \times 10^{-23} \, J/K)(273 \, K)} = 1.34 \times 10^{22} \, molecules\]
L'importance N est énorme, même en petits volumes. Par exemple,\(1 \, cm^3\) d'un gaz au STP contient des\(2.68 \times 10^{19} \) molécules. Encore une fois, notez que notre résultat pour l'azote est le même pour tous les types de gaz, y compris les mélanges.
Comme nous l'avons observé dans le chapitre sur la mécanique des fluides, les pascals\(N/m^2\) le sont également\(Pa \cdot m^3 = N \cdot m = J\). Ainsi, notre résultat pour N est sans dimension, un nombre pur qui pourrait être obtenu en comptant (en principe) plutôt qu'en mesurant. Comme il s'agit du nombre de molécules, nous plaçons « molécules » après le nombre, en gardant à l'esprit qu'il s'agit d'une aide à la communication plutôt que d'une unité.
Numéro de Moles et Avogadro
Il est souvent pratique de mesurer la quantité de substance avec une unité plus humaine que des molécules. L'unité SI utilisée à cette fin a été développée par le scientifique italien Amedeo Avogadro (1776—1856). (Il est parti de l'hypothèse selon laquelle des volumes égaux de gaz à pression et température égales contiennent un nombre égal de molécules, indépendamment du type de gaz. Comme indiqué ci-dessus, cette hypothèse a été confirmée lorsque l'approximation du gaz idéal s'applique.) Une mole (en abrégé mol) est définie comme la quantité de toute substance contenant autant de molécules qu'il y a d'atomes dans exactement 12 grammes (0,012 kg) de carbone 12. (Techniquement, nous devrions parler d' « unités de formule » et non de « molécules », mais cette distinction n'est pas pertinente pour nos besoins.) Le nombre de molécules dans une mole est appelé nombre d'Avogadro (\(N_A\)) et la valeur du nombre d'Avogadro est maintenant connue pour être\[N_A = 6.02 \times 10^{-23} \, mol^{-1}\]. On peut maintenant écrire\(N = N_An\), où n représente le nombre de moles d'une substance.
Le nombre d'Avogadro relie la masse d'une quantité de substance en grammes au nombre de protons et de neutrons dans un atome ou une molécule (12 pour un atome de carbone 12), ce qui détermine approximativement sa masse. Il est naturel de définir une unité de masse de telle sorte que la masse d'un atome soit approximativement égale à son nombre de neutrons et de protons. L'unité de ce type acceptée pour être utilisée avec le SI est l'unité de masse atomique unifiée (u), également appelée dalton. Plus précisément, un atome de carbone 12 a une masse d'exactement 12 u, de sorte que sa masse molaire M en grammes par mole est numériquement égale à la masse d'un atome de carbone 12 dans u. Cette égalité vaut pour toutes les substances. En d'autres termes,\(N_A\) ce n'est pas seulement la conversion du nombre de molécules en moles, mais c'est aussi la conversion de u en grammes :\(6.02 \times 10^{23} \, u = 1 \, g\). Voir la figure\(\PageIndex{5}\).
La quantité quotidienne recommandée de vitamine\(B_3\) ou de niacine\(C_6NH_5O_2\), pour les femmes qui ne sont pas enceintes ou qui n'allaitent pas, est de 14 mg. Déterminez le nombre de molécules de niacine dans cette quantité.
- Réponse
-
Nous devons d'abord calculer la masse molaire (la masse d'une mole) de la niacine. Pour ce faire, il faut multiplier le nombre d'atomes de chaque élément de la molécule par la masse molaire de l'élément.
(6 moles de carbone) (12,0 g/mol) + (5 mol d'hydrogène) (1,0 g/mol) + (1 mol d'azote) (14 g/mol) + (2 mol d'oxygène) (16,0 g/mol) = 123 g/mol
Ensuite, nous devons calculer le nombre de moles dans 14 mg.
\(\left(\dfrac{14 \, mg}{123 \, g/mol}\right)\left(\dfrac{1 \, g}{1000 \, mg}\right) = 1.14 \times 10^{-4} \, mol.\)
Ensuite, nous utilisons le nombre d'Avogadro pour calculer le nombre de molécules :
\(N = nN_A = (1.14 \times 10^{-4} \, mol)(6.02 \times 10^{23} \, molecules/mol) = 6.85 \times 10^{19} molecules\)
La densité de l'air dans une classe\(T = 20^oC\) (\((p = 1.00 \, atm\)et) est de\(1.28 \, kg/m^3\). À quelle pression se trouve la densité\(0.600 \, kg/m^3\) si la température est maintenue constante ?
- Réponse
-
La densité d'un gaz est égale à une constante, la masse moléculaire moyenne multipliée par la densité numérique N/V. C'est ce que nous voyons dans la\(pV = Nk_BT\) loi sur le gaz idéal\(N/V = p/k_BT\). Par conséquent, à température constante, si la densité et, par conséquent, la densité numérique sont réduites de moitié, la pression doit également être réduite de moitié, et\(p_f = 0.500 \, atm\).
La loi du gaz idéal reformulée en utilisant des taupes
Une expression très courante de la loi des gaz idéaux utilise le nombre de moles dans un échantillon, n, plutôt que le nombre de molécules, N. Nous partons de la loi idéale sur le gaz,
\[pV = Nk_BT,\]
et multipliez et divisez le côté droit de l'équation par le nombre d'Avogadro\(N_A\). Cela nous donne\[pV = \dfrac{N}{N_A}N_A k_BT.\]
Notez que\(n = N/N_A\) c'est le nombre de moles. Nous définissons la constante de gaz universelle comme\(R = N_Ak_B\) et obtenons la loi des gaz idéale en termes de moles.
En termes de nombre de moles n, la loi du gaz idéal s'écrit\[pV = nRT.\]
En unités SI,
\[R = N_Ak_B = (6.02 \times 10^{23} \, mol^{-1}) (1.38 \times 10^{-23} J/K) = 8.31 \, J/mol \cdot K\]
Dans les autres unités,
\[R = 1.99 \dfrac{cal}{mol \cdot K} = 0.0821 \dfrac{L \cdot atm}{mol \cdot K}.\]
Vous pouvez utiliser la valeur de R qui convient le mieux à un problème particulier.
Calculez la densité de l'air sec (a) dans des conditions standard et (b) dans une montgolfière à une température de\(120^oC\). L'air sec est d'environ\(78\% N_2, \, 21\% O_2,\) et\(1\% \, Ar\).
Stratégie et solution
- On nous demande de trouver la densité, ou la masse par mètre cube. Nous pouvons commencer par déterminer la masse molaire. Si nous avons cent molécules, dont 78 sont de l'azote, 21 de l'oxygène et 1 de l'argon, la masse moléculaire moyenne est de\(frac{78 \, m_{N_2} + 21 \, m_{O_2} + m_{Ar}}{100}\), ou la masse de chaque constituant multipliée par son pourcentage. Il en va de même pour la masse molaire, qui est donc\[M = 0.78 \, M_{N_2} + 0,21 \, M_{O_2} + 0.01 \, M_{Ar} = 29.0 \, g/mol.\] maintenant, nous pouvons trouver le nombre de moles par mètre cube. Nous utilisons la loi des gaz idéale en termes de moles\(pV = nRT\),, avec\(p = 1.00 \, atm\)\(T = 273 \, K\),\(V = 1 \, m^3\), et\(R = 8.31 \, J/mol \cdot K\). Le choix le plus pratique pour R dans ce cas est\(R = 8.31 \, J/mol \cdot K\) que les quantités connues sont en unités SI :\[n = \dfrac{pV}{RT} = \dfrac{(1.01 \times 10^5 \, Pa)(1 \, m^3)}{(8.31 \, J/mol \cdot K)(273 \, K)} = 44.5 \, mol.\] Ensuite, la masse\(m_s\) de cet air est\[m_s = nM = (44.5 \, mol)(29.0 \, g/mol) = 1290 \, g = 1.29 \, kg.\] Enfin la densité de l'air au STP est\[\rho = \dfrac{m_s}{V} = \dfrac{1.29 \, kg}{1 \, m^3} = 1.29 \, kg/m^3.\]
- La pression de l'air à l'intérieur du ballon est toujours de 1 atm car le fond du ballon est ouvert à l'atmosphère. Le calcul est le même sauf que nous utilisons une température de\(120^oC\) 393 K. Nous pouvons répéter le calcul en (a), ou simplement observer que la densité est proportionnelle au nombre de moles, qui est inversement proportionnel à la température. Ensuite, en utilisant les indices 1 pour l'air au STP et 2 pour l'air chaud, nous avons\[\rho_2 = \dfrac{T_1}{T_2}\rho_1 = \dfrac{273 \, K}{393 \, K}(1.29 \, kg/m^3) = 0.896 \, kg/m^3.\]
L'importance
En utilisant les méthodes du principe et de la flottabilité d'Archimède, nous pouvons constater que la force nette exercée par\(2200 \, m^3\) l'air\(120^oC\) est\(F_b - F_g = \rho_{atmosphere}V_g - \rho_{hot \, air}V_g = 8.49 \times 10^3 \, N\) suffisante pour soulever environ 867 kg. La masse volumique et la densité molaire de l'air au STP, présentées ci-dessus, sont souvent des valeurs utiles. À partir de la densité molaire, nous pouvons facilement déterminer un autre nombre utile, le volume d'une mole de tout gaz idéal à la STP, qui est de 22,4 L.
Les liquides et les solides ont des densités de l'ordre de 1000 fois supérieures à celles des gaz. Expliquez en quoi cela implique que les distances entre les molécules des gaz sont de l'ordre de 10 fois supérieures à la taille de leurs molécules.
- Réponse
-
La densité est la masse par unité de volume, et le volume est proportionnel à la taille d'un corps (comme le rayon d'une sphère) cubique. Donc, si la distance entre les molécules augmente d'un facteur 10, alors le volume occupé augmente d'un facteur 1000 et la densité diminue d'un facteur 1000. Comme nous supposons que les molécules sont en contact dans les liquides et les solides, la distance entre leurs centres est de l'ordre de leur taille habituelle, de sorte que la distance dans les gaz est de l'ordre de 10 fois plus grande.
La loi du gaz idéal est étroitement liée à l'énergie : les unités des deux côtés de l'équation sont les joules. Le côté droit de l'équation idéale de la loi des gaz est\(Nk_BT\). Ce terme correspond approximativement à l'énergie cinétique de translation totale (qui, lorsqu'on parle de gaz, fait référence à l'énergie de translation d'une molécule, et non à celle de la vibration de ses atomes ou de la rotation) des molécules N à une température absolue T, comme nous le verrons formellement dans la section suivante. Le côté gauche de l'équation idéale de la loi des gaz est pV. Comme mentionné dans l'exemple sur le nombre de molécules dans un gaz idéal, la pression multipliée par le volume a des unités d'énergie. L'énergie d'un gaz peut être modifiée lorsque le gaz agit à mesure que son volume augmente, ce que nous avons exploré dans le chapitre précédent, et que la quantité de travail est liée à la pression. C'est le processus qui se produit dans les moteurs à essence ou à vapeur et les turbines, comme nous le verrons dans le chapitre suivant.
- Étape 1. Examinez la situation pour déterminer s'il s'agit d'un gaz idéal. La plupart des gaz sont presque idéaux, sauf s'ils sont proches du point d'ébullition ou à des pressions bien supérieures à la pression atmosphérique.
- Étape 2. Dressez une liste des quantités données ou pouvant être déduites du problème tel qu'indiqué (identifiez les quantités connues).
- Étape 3. Identifiez exactement ce qui doit être déterminé dans le problème (identifiez les quantités inconnues). Une liste écrite est utile.
- Étape 4. Déterminez si le nombre de molécules ou le nombre de moles est connu ou demandé afin de décider s'il faut utiliser la loi des gaz idéaux\( pV = Nk_BT\), où N est le nombre de molécules ou\(pV = nRT\) où n est le nombre de moles.
- Étape 5. Convertissez les valeurs connues en unités SI appropriées (K pour la température, Pa pour la pression,\(m^3\) pour le volume, molécules pour N et moles pour n). Si les unités des valeurs connues sont cohérentes avec l'une des valeurs non SI de R, vous pouvez les laisser dans ces unités. Veillez à utiliser la température et la pression absolues.
- Étape 6. Résolvez la loi des gaz idéale pour la quantité à déterminer (la quantité inconnue). Vous devrez peut-être établir un ratio entre les états finaux et les états initiaux pour éliminer les quantités inconnues qui restent fixes.
- Étape 7. Substituez les quantités connues, ainsi que leurs unités, dans l'équation appropriée et obtenez des solutions numériques complètes avec des unités.
- Étape 8. Vérifiez la réponse pour voir si elle est raisonnable : est-ce logique ?
L'équation d'État de Van der Waals
Nous avons remarqué à plusieurs reprises que la loi idéale sur les gaz est une approximation. Comment l'améliorer ? L'équation d'état de Van der Waals (nommée d'après le physicien néerlandais Johannes van der Waals, 1837−1923) l'améliore en prenant en compte deux facteurs. Tout d'abord, les forces d'attraction entre les molécules, qui sont plus fortes à haute densité et réduisent la pression, sont prises en compte en ajoutant à la pression un terme égal au carré de la densité molaire multiplié par un coefficient a positif. Ensuite, le volume des molécules est représenté par une constante positive b, qui peut être considérée comme le volume d'une mole de molécules. Il est soustrait du volume total pour obtenir le volume restant dans lequel les molécules peuvent se déplacer. Les constantes a et b sont déterminées expérimentalement pour chaque gaz. L'équation qui en résulte est
\[ \left[p + a\left(\dfrac{n}{V}\right)^2\right] (V - nb) = nRT.\]
Dans la limite de la faible densité (petit n), les termes a et b sont négligeables, et nous avons la loi des gaz idéale, comme nous le devrions pour une faible densité. En revanche, si elle\(V - nb\) est petite, c'est-à-dire que les molécules sont très proches les unes des autres, la pression doit être plus élevée pour obtenir le même NRT, comme on peut s'y attendre dans le cas d'un gaz hautement comprimé. Cependant, l'augmentation de pression est inférieure à ce que suggère cet argument, car à haute densité, le\((n/V)^2\) terme est significatif. Comme elle est positive, elle entraîne une baisse de la pression pour obtenir le même NRT.
L'équation d'état de Van der Waals fonctionne bien pour la plupart des gaz dans des conditions très diverses. Comme nous le verrons dans le module suivant, il prédit même la transition gaz-liquide.
Schémas PV
Nous pouvons examiner certains aspects du comportement d'une substance en traçant un diagramme pV, qui est un graphique de la pression par rapport au volume. Lorsque la substance se comporte comme un gaz idéal, la loi du gaz idéal\(pV = nRT\) décrit la relation entre sa pression et son volume. Sur un diagramme pV, il est courant de tracer une isotherme, c'est-à-dire une courbe représentant p en fonction de V avec le nombre de molécules et la température fixes. Ensuite, pour un gaz idéal, par\(pV = constant.\) exemple, le volume du gaz diminue à mesure que la pression augmente. Le graphique qui en résulte est une hyperbole.
Cependant, si nous supposons l'équation d'état de Van der Waals, les isothermes deviennent plus intéressants, comme le montre la Figure\(\PageIndex{6}\). À des températures élevées, les courbes sont approximativement des hyperboles, représentant un comportement approximativement idéal à diverses températures fixes. À des températures plus basses, les courbes ressemblent de moins en moins à des hyperboles, c'est-à-dire que le gaz ne se comporte pas de manière idéale. Il existe une température critique\(T_c\) à laquelle la courbe a un point avec une pente nulle. En dessous de cette température, les courbes ne diminuent pas de façon monotone ; elles présentent chacune une « bosse », ce qui signifie que pour une certaine plage de volume, l'augmentation du volume augmente la pression.
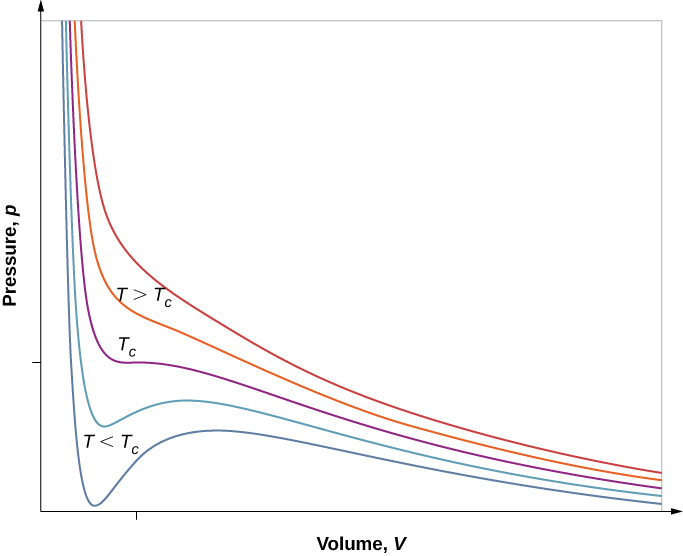
Un tel comportement serait totalement imphysique. Les courbes sont plutôt comprises comme décrivant une transition de phase liquide-gaz. La partie oscillante de la courbe est remplacée par une ligne horizontale, montrant que lorsque le volume augmente à température constante, la pression reste constante. Ce comportement correspond à l'ébullition et à la condensation ; lorsqu'une substance est à sa température d'ébullition pour une pression donnée, son volume peut augmenter à mesure qu'une partie du liquide se transforme en gaz, ou diminuer lorsqu'une partie du gaz se transforme en liquide, sans aucun changement de température ou de pression.
La figure\(\PageIndex{7}\) montre des isothermes similaires qui sont plus réalistes que celles basées sur l'équation de Van der Waals. Les parties raides des courbes situées à gauche de la zone de transition montrent la phase liquide, qui est presque incompressible ; une légère diminution de volume nécessite une augmentation importante de la pression. Les parties plates montrent la transition liquide-gaz ; les régions bleues qu'elles définissent représentent des combinaisons de pression et de volume où le liquide et le gaz peuvent coexister.
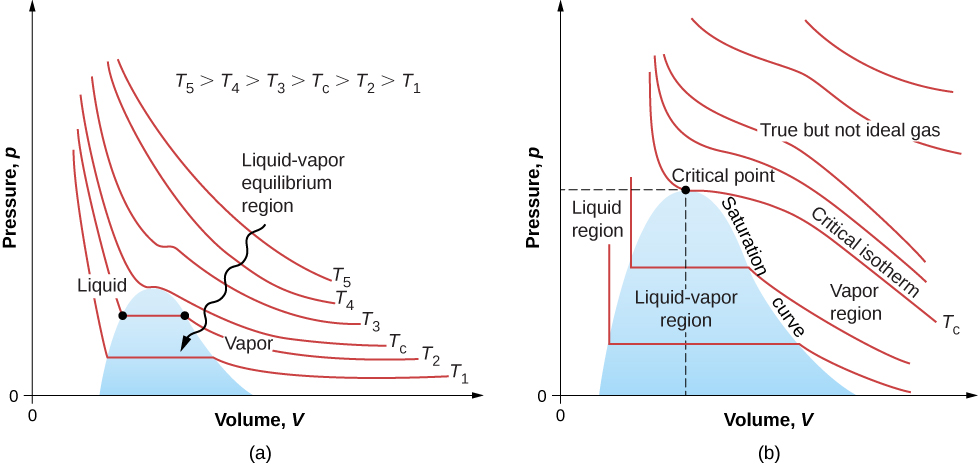
Les isothermes ci-dessus\(T_c\) ne passent pas par la transition liquide-gaz. Par conséquent, le liquide ne peut pas exister au-dessus de cette température, qui est la température critique (décrite dans le chapitre sur la température et la chaleur). À une pression suffisamment basse au-dessus de cette température, le gaz a la densité d'un liquide mais ne se condense pas ; le gaz est dit supercritique. À haute pression, il est solide. Le dioxyde de carbone, par exemple, ne contient pas de phase liquide à une température supérieure\(31.0^oC\). La pression critique est la pression maximale à laquelle le liquide peut exister. Le point du diagramme pV à la pression et à la température critiques est le point critique (que vous avez découvert dans le chapitre sur la température et la chaleur). Le tableau répertorie les températures et pressions critiques représentatives.
| Substance | Température critique | \(T_c\) | Pression critique | |
|---|---|---|---|---|
| K | \ (T_c \) « >\(^oC\) | Pennsylvanie | guichet automatique | |
| Eau | 647,4 | \ (T_c \) « >374,3 | \(22.12 \times 10^6\) | 219,0 |
| Dioxyde de soufre | 430,7 | \ (T_c \) « >157,6 | \(7.88\times 10^6\) | 78,0 |
| ammoniaque | 405,5 | \ (T_c \) « >132,4 | \(11.28\times 10^6\) | 111,7 |
| Dioxyde de carbone | 304,2 | \ (T_c \) « >31,1 | \(7.39\times 10^6\) | 73,2 |
| L'oxygène | 154,8 | \ (T_c \) « >—118,4 | \(5.08\times 10^6\) | 50,3 |
| azote | 126,2 | \ (T_c \) « >—146,9 | \(3.39\times 10^6\) | 33,6 |
| Hydrogène | 33,3 | \ (T_c \) « >—239,9 | \(1.30\times 10^6\) | 12,9 |
| Hélium | 5.3 | \ (T_c \) « >—267,9 | \(0.229\times 10^6\) | 2,27 |


