11.E : Physique des particules et cosmologie (exercices)

Questions conceptuelles

11.1 Introduction à la physique des particules

1. Quelles sont les quatre forces fondamentales ? Décrivez-les brièvement.

2. Distinguer les fermions et les bosons en utilisant les concepts d'indissociabilité et de symétrie d'échange.

3. Listez les familles de quarks et de leptons

4. Distinguer les particules élémentaires des antiparticules. Décrivez leurs interactions.

11.2 Lois sur la conservation des particules

5. Quelles sont les six lois de conservation des particules ? Décrivez-les brièvement.

6. En général, comment déterminer si une réaction ou une désintégration des particules se produit ?

7. Pourquoi la détection d'interactions entre particules violant une loi établie sur la conservation des particules pourrait-elle être considérée comme une bonne chose pour un scientifique ?

11.3 Quarks

8. Quels sont les six quarks connus ? Résumez leurs propriétés.

9. Quelle est la composition générale en quarks d'un baryon ? D'un méson ?

10. Quelles sont les preuves de l'existence des quarks ?

11. Pourquoi les baryons ayant la même composition en quarks diffèrent-ils parfois dans leurs énergies massiques de repos ?

11.4 Accélérateurs et détecteurs de particules

12. Comparez brièvement l'accélérateur Van de Graaff, l'accélérateur linéaire, le cyclotron et l'accélérateur synchrotron.

13. Décrire les composants et les fonctions de base d'une machine à faisceau de collision typique.

14. Quels sont les sous-détecteurs de l'expérience Compact Muon Solenoid ? Décrivez-les brièvement.

15. Quel est l'avantage d'un accélérateur à faisceau de collision par rapport à un accélérateur qui projette des particules sur une cible fixe ?

16. Un électron apparaît dans les détecteurs de muons du CMS. Comment est-ce possible ?

11.5 Le modèle standard

17. Qu'est-ce que le modèle standard ? Exprimez votre réponse en fonction des quatre forces fondamentales et échangez des particules.

18. Dessinez un diagramme de Feynman pour représenter l'annihilation d'un électron et d'un positron en photon.

19. Quelle est la motivation des théories de la grande unification ?

20. Si l'on développe une théorie qui unifie les quatre forces, sera-t-il toujours correct de dire que l'orbite de la Lune est déterminée par la force gravitationnelle ? Expliquez pourquoi.

21. Si le boson de Higgs est découvert et s'il s'avère qu'il a une masse, sera-t-il considéré comme le vecteur ultime de la force faible ? Expliquez votre réponse.

22. L'un des modes de désintégration les plus courants de l'\(\displaystyle Λ^0\)est\(\displaystyle Λ^0→π^−+p\). Même si seuls les hadrons sont impliqués dans cette désintégration, elle se produit par le biais de la faible force nucléaire. Comment savons-nous que cette dégradation ne se produit pas grâce à la puissante force nucléaire ?

11.6 Le Big Bang

23. Qu'entend-on par expansion cosmologique ? Exprimez votre réponse sous la forme d'un graphe de Hubble et du décalage vers le rouge de la lumière lointaine des étoiles.

24. Décrivez l'analogie du ballon pour l'expansion cosmologique. Expliquez pourquoi il apparaît simplement que nous sommes au centre de l'expansion de l'univers.

25. Les distances par rapport aux galaxies locales sont déterminées en mesurant la luminosité des étoiles, appelées variables céphéides, qui peuvent être observées individuellement et dont la luminosité absolue à une distance standard est bien connue. Expliquez comment la luminosité mesurée varierait en fonction de la distance, par rapport à la luminosité absolue.

11.7 Évolution de l'univers primitif

26. Qu'entend-on par « modèle cosmologique des débuts de l'univers » ? Décrivez brièvement ce modèle en fonction des quatre forces fondamentales.

27. Décrivez deux éléments de preuve qui soutiennent le modèle du Big Bang.

28. Dans quel sens sommes-nous, comme Newton l'a dit un jour, « un garçon qui joue au bord de la mer » ? Exprimez votre réponse en termes de concepts de matière noire et d'énergie noire.

29. Si une cause inconnue du décalage vers le rouge, telle que la « fatigue » de la lumière après avoir parcouru de longues distances dans l'espace vide, était découverte, quel effet cela aurait-il sur la cosmologie ?

30. Dans le passé, de nombreux scientifiques croyaient que l'univers était infini. Cependant, si l'univers est infini, n'importe quelle ligne de visée devrait finir par tomber sur la surface d'une étoile et le ciel nocturne devrait être très brillant. Comment résoudre ce paradoxe dans la cosmologie moderne ?

Problèmes

11.1 Introduction à la physique des particules

31. Quelle quantité d'énergie est libérée lorsqu'un électron et un positron s'annihilent mutuellement au repos ? (Pour les masses de particules, voir le tableau 11.1.)

32. Si\(\displaystyle 1.0×10^{30}MeV\) de l'énergie est libérée lors de l'annihilation d'une sphère de matière et d'antimatière, et que les sphères ont une masse égale, quelles sont les masses des sphères ?

33. Lorsqu'un électron et un positron sont au repos, ils peuvent s'annihiler mutuellement en fonction de la réaction\(\displaystyle e^−+e^+→γ+γ\). Dans ce cas, quelles sont l'énergie, la quantité de mouvement et la fréquence de chaque photon ?

34. Quelle est l'énergie cinétique totale emportée par les particules des désintégrations suivantes ?

(a)\(\displaystyle π^0→γ+γ\)

(b)\(\displaystyle K^0→π^++π^−\)

(c)\(\displaystyle \sum{}^+→n+π^+\)

(d)\(\displaystyle \sum{}^0→Λ^0+γ\).

11.2 Lois sur la conservation des particules

35. Laquelle des désintégrations suivantes ne peut pas se produire en raison d'une violation de la loi de conservation du nombre de leptons ?

(a)\(\displaystyle n→p+e^−\)

(b)\(\displaystyle μ^+→e^++\bar{\nu_e}\)

(c)\(\displaystyle π^+→e^++\nu_e+\bar{\nu_μ}\)

(d)\(\displaystyle p→n+e^++\nu_e\)

(e)\(\displaystyle π^−→e^−+\bar{\nu_e}\)

(f)\(\displaystyle μ^−→e^−+\bar{\nu_e}+\nu_μ\)

(g)\(\displaystyle Λ^0→π^−+p\)

(h)\(\displaystyle K^+→μ^++\nu_μ\)

36. Laquelle des réactions suivantes ne le peut pas parce que la loi de conservation de l'étrangeté est violée ?

(a)\(\displaystyle p+n→p+p+π^−\)

(b)\(\displaystyle p+n→p+p+K^−\)

(c)\(\displaystyle K^−+p→K^−+\sum{}^+\)

(d)\(\displaystyle π^−+p→K^++\sum{}^−\)

(e)\(\displaystyle K^−+p→Ξ^0+K^++π^−\)

(f)\(\displaystyle K^−+p→Ξ^0+π^−+π^−\)

(g)\(\displaystyle π^++p→\sum{}^++K^+\)

(h)\(\displaystyle π^−+n→K^−+Λ^0\)

37. Identifiez une désintégration possible pour chacune des antiparticules suivantes :

(a)\(\displaystyle \bar{n}\),

(b)\(\displaystyle \bar{Λ^0}\),

(c)\(\displaystyle Ω^+\),

(d)\(\displaystyle K^−\), et

(e)\(\displaystyle \bar{\sum{}}\).

38. Chacune des réactions nucléaires fortes suivantes est interdite. Identifiez une loi de conservation qui est violée pour chacun d'entre eux.

(a)\(\displaystyle p+\bar{p}→p+n+\bar{p}\)

(b)\(\displaystyle p+n→p+\bar{p}+n+π^+\)

(c)\(\displaystyle π^−+p→\sum{}^++K^−\)

(d)\(\displaystyle K^−+p→Λ^0+n\)

11.3 Quarks

39. Sur la base de la composition en quarks d'un proton, montrez que sa charge est\(\displaystyle +1\).

40. Sur la base de la composition en quarks d'un neutron, montrez que sa charge est nulle.

41. Soutenez que la composition en quarks donnée dans le tableau 11.5 pour le kaon positif correspond à la charge, au spin et à l'étrangeté connus de ce baryon.

42. Les mésons sont formés à partir des combinaisons suivantes de quarks (les indices indiquent la couleur et\(\displaystyle (AR=antired): (d_R,\bar{d_{AR}}), (s_G,\bar{u_{AG}})\), et\(\displaystyle (s_R,\bar{s_{AR}})\).

(a) Déterminez la charge et l'étrangeté de chaque combinaison.

(b) Identifier un ou plusieurs mésons formés par chaque combinaison quark-antiquark.

43. Pourquoi aucun des ensembles de quarks présentés ci-dessous ne peut-il former un hadron ?

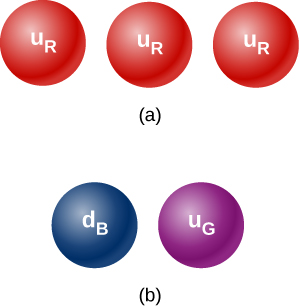
44. Les résultats expérimentaux indiquent une particule isolée chargée\(\displaystyle +2/3\), c'est-à-dire un quark isolé. De quel quark s'agit-il ? Pourquoi cette découverte serait-elle importante ?

45. Exprime les\(\displaystyle β\) désintégrations\(\displaystyle n→p+e^−+\bar{\nu}\) et\(\displaystyle p→n+e^++\nu\) en termes de\(\displaystyle β\) désintégrations des quarks. Vérifiez que les lois de conservation concernant la charge, le nombre de leptons et le nombre de baryons sont respectées par la\(\displaystyle β\) désintégration des quarks.

11.4 Accélérateurs et détecteurs de particules

46. Une particule chargée dans un champ magnétique de 2,0 T est courbée dans un cercle d'un rayon de 75 cm. Quelle est la quantité de mouvement de la particule ?

47. Une trace de protons traverse un champ magnétique d'un rayon de 50 cm. L'intensité du champ magnétique est de 1,5 T. Quelle est l'énergie totale du proton ?

48. Dérivez l'équation\(\displaystyle p=0.3Br\) en utilisant les concepts d'accélération centripète (mouvement en deux et trois dimensions) et de moment relativiste (relativité)

49. Supposons que l'énergie du faisceau d'un collisionneur électron-positon est d'environ 4,73 GeV. Quelle est la masse totale (W) d'une particule produite lors de l'annihilation d'un électron et d'un positron dans ce collisionneur ? Quel méson pourrait être produit ?

50. À pleine énergie, les protons du synchrotron Fermilab de 2 km de diamètre se déplacent presque à la vitesse de la lumière, puisque leur énergie est environ 1 000 fois l'énergie de leur masse restante.

(a) Combien de temps faut-il à un proton pour effectuer un voyage ?

(b) Combien de fois par seconde traversera-t-il la zone cible ?

51. Supposons qu'un objet\(\displaystyle W^−\) créé dans un détecteur de particules perdure\(\displaystyle 5.00×10^{−25}s\). Quelle distance se déplace-t-il pendant cette période s'il se déplace à 0,900 °C ? (Notez que le temps est plus long que la durée de\(\displaystyle W^−\) vie donnée, ce qui peut être dû à la nature statistique de la décroissance ou de la dilatation temporelle.)

52. Quelle est la longueur d'une piste qui\(\displaystyle π^+\) se déplace à 0,100 °C dans une chambre à bulles si elle y est créée et si elle vit\(\displaystyle 2.60×10^{−8}s\) ? (Les personnes qui se déplacent plus vite ou vivent plus longtemps peuvent échapper au détecteur avant de se décomposer.)

53. Le SLAC de 3,20 km de long produit un faisceau d'électrons de 50,0 GeV. S'il y a 15 000 tubes accélérateurs, quelle tension moyenne doit être présente à travers les interstices entre eux pour obtenir cette énergie ?

11.5 Le modèle standard

54. À l'aide du principe d'incertitude de Heisenberg, déterminez la plage de la force faible si cette force est produite par l'échange d'un boson Z.

55. Utilisez le principe d'incertitude de Heisenberg pour estimer la portée d'une désintégration nucléaire faible impliquant un graviton.

56. (a) La désintégration suivante est médiée par la force électrofaible :\(\displaystyle p→n+e^++\nu_e\). Dessine le diagramme de Feynman pour la décomposition.

(b) La diffusion suivante est médiée par la force électrofaible :\(\displaystyle \nu_e+e^−→\nu_e+e^−\). Dessinez le diagramme de Feynman pour la diffusion.

57. En supposant une conservation de l'élan, quelle est l'énergie de chaque\(\displaystyle γ\) rayon produit lors de la désintégration d'un pion neutre au repos, lors de la réaction\(\displaystyle π^0→γ+γ\) ?

58. Quelle est la longueur d'onde d'un électron de 50 GeV produit au SLAC ? Cela donne une idée de la limite des détails qu'il peut sonder.

59. Le mode de désintégration principal pour le pion négatif est\(\displaystyle π^−→μ^−+\bar{\nu_μ}\).

(a) Quelle est la libération d'énergie en MeV lors de cette désintégration ?

(b) En utilisant la conservation de l'élan, quelle quantité d'énergie reçoit chacun des produits de désintégration, étant donné qu'ils\(\displaystyle π^−\) sont au repos lorsqu'ils se désintègrent ? Vous pouvez supposer que l'antineutrino muonique est sans masse et possède un élan\(\displaystyle p=E/c\), tout comme un photon.

60. Supposons que vous conceviez une expérience de désintégration des protons et que vous puissiez détecter 50 % des désintégrations de protons dans un réservoir d'eau.

(a) Combien de kilogrammes d'eau auriez-vous besoin pour observer une décomposition par mois, en supposant une durée de vie de\(\displaystyle 10^{31}\) y ?

(b) De combien de mètres cubes d'eau s'agit-il ?

(c) Si la durée de vie réelle est\(\displaystyle 10^{33}y\), combien de temps devriez-vous attendre en moyenne pour voir un seul proton se désintégrer ?

11.6 Le Big Bang

61. Si la vitesse d'une galaxie lointaine est de 0,99 c, quelle est la distance entre la galaxie et un observateur se dirigeant vers la Terre ?

62. La distance entre une galaxie et notre système solaire est de 10 Mpc.

(a) Quelle est la vitesse de récession de la galaxie ?

(b) De quelle fraction la lumière des étoiles de cette galaxie est-elle décalée vers le rouge (c'est-à-dire quelle est sa valeur z) ?

63. Si une galaxie se trouve à 153 Mpc de nous, à quelle vitesse pensons-nous qu'elle se déplace et dans quelle direction ?

64. En moyenne, à quelle distance se trouvent les galaxies qui s'éloignent de nous en\(\displaystyle 2.0%\) % de la vitesse de la lumière ?

65. Notre système solaire tourne autour du centre de la Voie lactée. En supposant une orbite circulaire de 30 000 ly de rayon et une vitesse orbitale de 250 km/s, combien d'années faut-il pour un tour ? Notez que c'est approximatif, en supposant une vitesse constante et une orbite circulaire, mais qu'il est représentatif du temps nécessaire à notre système et aux étoiles locales pour faire une révolution autour de la galaxie.

66. (a) Quelle est la vitesse approximative par rapport à nous d'une galaxie située à la limite de l'univers connu, à une dizaine de kilomètres de distance ?

(b) De quelle fraction de la vitesse de la lumière s'agit-il ? Notez que nous avons observé des galaxies s'éloigner de nous à plus de 0,9 °C.

67. (a) Calculez l'âge approximatif de l'univers à partir de la valeur moyenne de la constante de Hubble,\(\displaystyle H_0=20km/s⋅Mly\). Pour ce faire, calculez le temps qu'il faudrait pour parcourir 0,307 Mpc à un taux d'expansion constant de 20 km/s.

(b) Si une accélération se produit d'une manière ou d'une autre, l'âge réel de l'univers serait-il supérieur ou inférieur à celui trouvé ici ? Expliquez.

68. La galaxie d'Andromède est la grande galaxie la plus proche et elle est visible à l'œil nu. Estimez sa luminosité par rapport au Soleil, en supposant qu'elle a une luminosité\(\displaystyle 10^{12}\) multipliée par celle du Soleil et qu'elle se trouve à 0,613 Mpc.

69. Montrez que la vitesse d'une étoile en orbite autour de sa galaxie sur une orbite circulaire est inversement proportionnelle à la racine carrée de son rayon orbital, en supposant que la masse des étoiles à l'intérieur de son orbite agit comme une masse unique au centre de la galaxie. Vous pouvez utiliser une équation d'un chapitre précédent pour étayer votre conclusion, mais vous devez justifier son utilisation et définir tous les termes utilisés.

Problèmes supplémentaires

70. Les résultats expérimentaux suggèrent qu'un muon se désintègre en électron et en photon. Comment est-ce possible ?

71. Il manque une seule particule à chacune des réactions suivantes. Identifiez la particule manquante pour chaque réaction.

(a)\(\displaystyle p+\bar{p}→n+?\)

(b)\(\displaystyle p+p→p+Λ^0+?\)

(c)\(\displaystyle π^{−}+p→\sum{}^−+?\)

(d)\(\displaystyle K^−+n→Λ^0+?\)

(e)\(\displaystyle τ^+→e^++\nu_e+?\)

(f)\(\displaystyle \bar{\nu_e}+p→n+?\)

72. En raison de la perte d'énergie due au rayonnement synchrotron dans le LHC du CERN, seuls 5 MeV sont ajoutés à l'énergie de chaque proton lors de chaque révolution autour de l'anneau principal. Combien de tours sont nécessaires pour produire des protons de 7,00 TeV (7 000 GeV), s'ils sont injectés avec une énergie initiale de 8,00 GeV ?

73. Un proton et un antiproton entrent en collision frontale, chacun ayant une énergie cinétique de 7,00 TeV (comme dans le LHC du CERN). Quelle est la quantité d'énergie de collision disponible, compte tenu de l'anéantissement des deux masses ? (Notez que cette énergie n'est pas significativement supérieure à l'énergie cinétique extrêmement relativiste.)

74. Lorsqu'un électron et un positron entrent en collision à l'installation SLAC, ils ont chacun une énergie cinétique de 50,0 GeV. Quelle est l'énergie totale de collision disponible, compte tenu de l'énergie d'annihilation ? Notez que l'énergie d'annihilation est insignifiante, car les électrons sont très relativistes.

75. Le cœur d'une étoile s'effondre lors d'une supernova, formant une étoile à neutrons. Le moment cinétique du noyau est conservé, de sorte que l'étoile à neutrons tourne rapidement. Si le rayon initial du noyau est\(\displaystyle 5.0×10^5km\) et qu'il s'effondre à 10,0 km, déterminez la vitesse angulaire de l'étoile à neutrons en tours par seconde, étant donné que la vitesse angulaire du noyau était initialement de 1 révolution tous les 30 jours.

76. En utilisant la solution du problème précédent, déterminez l'augmentation de l'énergie cinétique de rotation, étant donné que la masse du noyau est 1,3 fois supérieure à celle de notre Soleil. D'où vient cette augmentation de l'énergie cinétique ?

77. (a) Quelle constante de Hubble correspond à l'âge approximatif de l'univers de\(\displaystyle 10^{10}\) y ? Pour obtenir une valeur approximative, supposons que le taux d'expansion est constant et calculez la vitesse à laquelle deux galaxies doivent s'éloigner pour être séparées par 1 million (séparation galactique moyenne actuelle) en un temps\(\displaystyle 10^{10}\) y.

(b) De même, quelle constante de Hubble correspond à un univers vieux d'environ\(\displaystyle 2×10^{10}\) plusieurs années ?

Problèmes liés au défi

78. Les électrons et les positrons entrent en collision dans un accélérateur circulaire. Dérivez l'expression de l'énergie du centre de masse de la particule.

79. L'intensité du rayonnement cosmique diminue rapidement à mesure que l'énergie augmente, mais il arrive que des rayons cosmiques extrêmement énergétiques créent une pluie de rayonnement à partir de toutes les particules qu'ils créent en frappant un noyau dans l'atmosphère. Supposons qu'une particule de rayon cosmique ayant une énergie de\(\displaystyle 10^{10}GeV\) convertit son énergie en particules dont la masse est calculée en moyenne\(\displaystyle 200MeV/c^2\).

(a) Combien de particules sont créées ?

(b) Si les particules pleuvent sur une\(\displaystyle 1.00-km^2\) zone, combien de particules y a-t-il par mètre carré ?

80. (a) Calculer la quantité relativiste\(\displaystyle γ=1\frac{1}{\sqrt{1−v^2/c^2}}\) des protons de 1,00 TeV produits au Fermilab.

(b) Si un tel proton\(\displaystyle π^+\) créait une vitesse identique, quelle serait sa durée de vie en laboratoire ?

(c) Quelle distance pourrait-elle parcourir à cette époque ?

81. Les plans d'un accélérateur qui produit un faisceau secondaire de mésons K à diffuser à partir des noyaux, dans le but d'étudier la force forte, exigent que ceux-ci aient une énergie cinétique de 500 MeV.

(a) Quelle serait la quantité\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) relativiste pour ces particules ?

(b) Quelle serait leur durée de vie moyenne en laboratoire ?

(c) Quelle distance pourraient-ils parcourir à cette époque ?

82. Dans les supernovae, les neutrinos sont produits en grandes quantités. Ils ont été détectés à partir de la supernova de 1987A dans le nuage de Magellan, situé à environ 120 000 années-lumière de la Terre (relativement proche de notre galaxie de la Voie lactée). Si les neutrinos ont une masse, ils ne peuvent pas se déplacer à la vitesse de la lumière, mais si leur masse est faible, leur vitesse serait presque celle de la lumière.

(a) Supposons qu'un neutrino ayant une\(\displaystyle 7-eV/c^2\) masse ait une énergie cinétique de 700 keV. Trouve la quantité\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) relativiste qui s'y rapporte.

(b) Si le neutrino quitte la supernova de 1987A en même temps qu'un photon et que les deux se rendent sur Terre, combien de temps plus tôt le photon arrive-t-il ? Ce décalage horaire n'est pas important, étant donné qu'il est impossible de savoir quel neutrino est resté avec quel photon et que les détecteurs de neutrinos sont peu efficaces. Ainsi, le fait que les neutrinos aient été observés quelques heures après l'éclaircissement de la supernova ne fait que fixer une limite supérieure à la masse du neutrino. (Conseil : il se peut que vous deviez utiliser une extension de série pour trouver v pour le neutrino, étant donné sa\(\displaystyle γ\) taille.)

83. En supposant une orbite circulaire du Soleil autour du centre de la Voie lactée, calculez sa vitesse orbitale à l'aide des informations suivantes : La masse de la galaxie équivaut à une seule masse\(\displaystyle 1.5×10^{11}\) multipliée par celle du Soleil (ou\(\displaystyle 3×10^{41}kg\)), situé à 30 000 miles de distance.

84. (a) Quelle est la force de gravité approximative sur une personne de 70 kg due à la galaxie d'Andromède, en supposant que sa masse totale est\(\displaystyle 10^{13}\) celle de notre Soleil et qu'elle agit comme une masse unique à 0,613 Mpc de distance ?

(b) Quel est le rapport entre cette force et le poids de la personne ? Notez qu'Andromède est la grande galaxie la plus proche.

85. (a) Une particule et son antiparticule sont au repos par rapport à un observateur et s'annihilent (détruisant complètement les deux masses), créant ainsi deux\(\displaystyle γ\) rayons d'énergie égale. Quelle est l'énergie caractéristique\(\displaystyle γ\) des rayons X que vous rechercheriez si vous recherchez des preuves d'annihilation proton-antiproton ? (Le fait que de tels rayonnements soient rarement observés prouve qu'il y a très peu d'antimatière dans l'univers.)

(b) Comment cela se compare-t-il à l'énergie de 0,511 MeV associée à l'annihilation électron-positon ?

86. L'intensité maximale du CMBR se produit à une longueur d'onde de 1,1 mm.

(a) Quelle est l'énergie en eV d'un photon de 1,1 mm ?

(b) Il y a environ des\(\displaystyle 10^9\) photons pour chaque particule massive dans l'espace lointain. Calculez l'énergie de\(\displaystyle 10^9\) tels photons.

(c) Si la masse d'une particule massive moyenne dans l'espace est la moitié de celle d'un proton, quelle énergie serait créée en convertissant sa masse en énergie ?

(d) Cela signifie-t-il que l'espace est « dominé par la matière » ? Expliquez brièvement.

87. (a) Utiliser le principe d'incertitude de Heisenberg pour calculer l'incertitude énergétique pour un intervalle de temps correspondant de\(\displaystyle 10^{−43}s\).

(b) Comparez cette énergie à l'énergie\(\displaystyle 10^{19}GeV\) d'unification des forces et expliquez pourquoi elles sont similaires.