8.4 : Spin des électrons
- Page ID
- 189795
À la fin de cette section, vous serez en mesure de :
- Exprime l'état d'un électron dans un atome d'hydrogène en termes de cinq nombres quantiques
- Utilisez des nombres quantiques pour calculer l'amplitude et la direction du spin et du moment magnétique d'un électron
- Expliquer la structure fine et hyperfine du spectre de l'hydrogène en termes d'interactions magnétiques à l'intérieur de l'atome d'hydrogène
Dans cette section, nous examinons les effets du spin des électrons. Spin introduit deux nombres quantiques supplémentaires dans notre modèle de l'atome d'hydrogène. Les deux ont été découverts en étudiant la structure fine des spectres atomiques. Le spin est une caractéristique fondamentale de toutes les particules, et pas seulement des électrons, et il est analogue au spin intrinsèque des corps étendus autour de leurs propres axes, comme la rotation quotidienne de la Terre.
Le spin est quantifié de la même manière que le moment cinétique orbital. Il a été découvert que l'amplitude du moment cinétique de spin intrinsèque\(S\) d'un électron est donnée par
\[S = \sqrt{s(s + 1)}\hbar, \nonumber \]
où\(s\) est défini comme étant le nombre quantique de spin. Ceci est similaire à la quantification de\(L\), sauf que la seule valeur autorisée\(s\) pour un électron est\(s = 1/2\). L'électron est considéré comme une « demi-particule de spin ». Le nombre quantique de projection de spin\(m_s\) est associé aux composantes z du spin, exprimées par
\[S_z = m_s\hbar. \label{eq2} \]
En général, les nombres quantiques autorisés sont
\[m_s = -s, -s + 1, . . ., 0, . . ., +s - 1, s. \nonumber \]
Pour le cas particulier d'un électron (\(s = 1/2\)),
\[m_s = -\frac{1}{2} \text{ or } \frac{1}{2}. \nonumber \]
Les directions du spin intrinsèque sont quantifiées, tout comme elles l'étaient pour le moment cinétique orbital. L'\(m_s = -1/2\)état est appelé état « spin-down » et possède une composante z de spin\(s_z = -1/2\), l'\(m_s = +1/2\)état est appelé état « spin-up » et possède une composante z de spin,\(s_z = +1/2\). Ces états sont illustrés dans la figure\(\PageIndex{1}\).
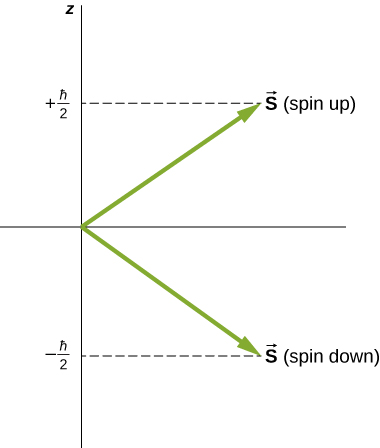
Le moment dipolaire magnétique intrinsèque d'un électron\(\mu_e\) peut également être exprimé en termes de nombre quantique de spin. Par analogie avec le moment cinétique orbital, l'amplitude du moment magnétique des électrons est
\[\mu_s = \left(\frac{e}{2m_e}\right)S. \nonumber \]
Selon la théorie spéciale de la relativité, cette valeur est faible d'un facteur 2. Ainsi, sous forme vectorielle, le moment magnétique de spin est
\[\vec{\mu} = \left(\frac{e}{m_e}\right)\vec{S}. \nonumber \]
La composante z du moment magnétique est (d'après l'équation \ ref {eq2})
\[\begin{align} \mu_z &= - \left(\frac{e}{m_e}\right) S_z \\[5pt] &= - \left(\frac{e}{m_e}\right) m_s \hbar. \end{align} \nonumber \]
Le nombre quantique de projection de spin n'a que deux valeurs (\(m_s = \pm1/2\)), de sorte que la composante z du moment magnétique n'a également que deux valeurs :
\[\mu_z = \pm \left(\frac{e}{2m_e}\right) = \pm \mu_B\hbar, \nonumber \]
où se\(\mu_B\) trouve un magnéton de Bohr. Un électron étant magnétique, nous nous attendons à ce qu'il interagisse avec d'autres champs magnétiques. Nous examinons deux cas particuliers : l'interaction d'un électron libre avec un champ magnétique externe (non uniforme) et d'un électron d'un atome d'hydrogène avec un champ magnétique produit par le moment cinétique orbital de l'électron.
Electron dans un champ externe
L'expérience Stern-Gerlach fournit des preuves expérimentales que les électrons ont un moment cinétique de spin. L'expérience fait passer un flux d'atomes d'argent (Ag) à travers un champ magnétique externe non uniforme. L'atome d'Ag a un moment cinétique orbital nul et contient un seul électron non apparié dans l'enveloppe extérieure. Par conséquent, le moment cinétique total de l'atome d'Ag est entièrement dû au spin de l'électron extérieur (\(s = 1/2\)). En raison du spin des électrons, les atomes d'Ag agissent comme de minuscules aimants lorsqu'ils traversent le champ magnétique. Ces « aimants » ont deux orientations possibles, qui correspondent aux états de rotation ascendante et descendante de l'électron. Le champ magnétique dévie les atomes de spin ascendant dans une direction et les atomes de spin descendant dans une autre direction. Cela produit deux bandes distinctes sur un écran (Figure\(\PageIndex{2}\)).
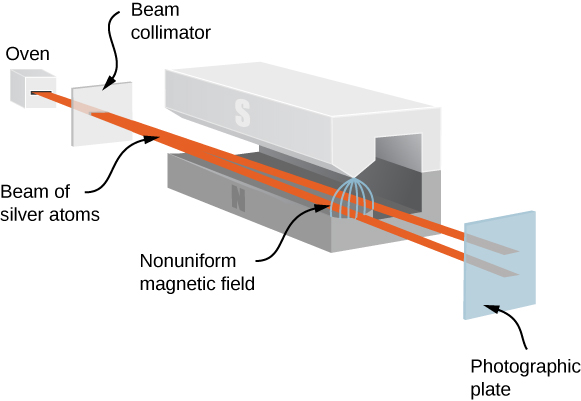
Selon les prédictions classiques, le moment cinétique (et donc le moment magnétique) de l'atome d'Ag peut pointer dans n'importe quelle direction. On s'attend donc à une tache continue sur l'écran. Les deux bandes de l'expérience de Stern-Gerlach qui en ont résulté fournissent un support surprenant aux idées de la mécanique quantique.
Visitez PhET Explorations : expérience de Stern-Gerlach pour en savoir plus sur l'expérience de Stern-Gerlach.
Un atome d'hydrogène à l'état fondamental est placé dans un champ magnétique uniforme externe (\(B = 1.5 \, T\)). Déterminez la fréquence du rayonnement produit lors d'une transition entre les états de spin-up et de spin-down de l'électron.
Stratégie
Le nombre quantique de projection de spin est\(m_s = \pm 1/2\), donc la composante z du moment magnétique est
\[\mu_z = \pm \left(\frac{e}{2m_e} \right) = \pm \mu_B \hbar. \nonumber \]
L'énergie potentielle associée à l'interaction entre le moment magnétique électronique et le champ magnétique externe est
\[\begin{align*} U &= - \mu_z B \\[5pt] &= \mp \mu_BB. \end{align*} \nonumber \]
La fréquence de la lumière émise est proportionnelle à la différence d'énergie (\(\Delta E\)) entre ces deux états.
Solution
La différence d'énergie entre ces états est de\(\Delta E = 2\mu_BB\), donc la fréquence du rayonnement produit est
\[\begin{align*} f = \dfrac{\Delta E}{h} &= \frac{2\mu_BB}{h} \\[5pt] &= \frac{2\left(5.79 \times \frac{10^{-5} eV}{T}\right)(1.5 \, T)}{4.136 \times 10^{-15} eV \cdot s} \\[5pt] &= 4.2 \times 10^{10} \, \frac{cycles}{s}. \end{align*} \nonumber \]
L'importance
Le moment magnétique des électrons est couplé au champ magnétique externe. L'énergie de ce système est différente que l'électron soit aligné ou non avec le proton. La fréquence du rayonnement produit par une transition entre ces états est proportionnelle à la différence d'énergie. Si nous doublons la force du champ magnétique, en maintenant toutes les autres choses constantes, la fréquence du rayonnement double et sa longueur d'onde est réduite de moitié.
Si l'expérience de Stern-Gerlach a produit quatre bandes distinctes au lieu de deux, que pourrait-on conclure quant au nombre quantique de spin de la particule chargée ?
- Réponse
-
\(s = 3/2 <\)
Couplage spin-orbite (structure fine)
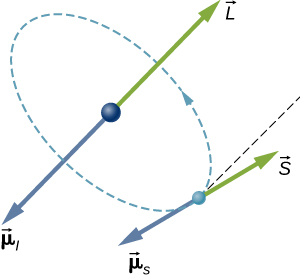
Dans un atome d'hydrogène, le moment magnétique de l'électron peut interagir avec le champ magnétique produit par le moment cinétique orbital de l'électron, un phénomène appelé couplage spin-orbite. Les vecteurs du moment cinétique orbital (\(\vec{L}\)), du moment magnétique orbital (\(\vec{\mu}\)), du moment cinétique de spin (\(\vec{S}\)) et du moment magnétique de spin (\(\vec{\mu}_s\)) sont représentés ensemble sur la Figure\(\PageIndex{3}\).
Tout comme les niveaux d'énergie d'un atome d'hydrogène peuvent être divisés par un champ magnétique externe, les niveaux d'énergie d'un atome d'hydrogène le sont également par les champs magnétiques internes de l'atome. Si le moment magnétique de l'électron et le moment magnétique orbital de l'électron sont antiparallèles, l'énergie potentielle provenant de l'interaction magnétique est relativement élevée, mais lorsque ces moments sont parallèles, l'énergie potentielle est relativement faible. Le passage de chacun de ces deux états à un niveau d'énergie inférieur entraîne l'émission d'un photon de fréquence légèrement différente. C'est-à-dire que le couplage spin-orbite « divise » la raie spectrale attendue d'un électron sans spin. La structure fine du spectre de l'hydrogène s'explique par le couplage spin-orbite.
Couplage de spin nucléaire entre électrons et spin (structure hyperfine)
Tout comme un électron, un proton est un spin 1/2 et possède un moment magnétique. (Selon la théorie nucléaire, ce moment est dû au mouvement orbital des quarks au sein du proton.) La structure hyperfine du spectre de l'hydrogène s'explique par l'interaction entre le moment magnétique du proton et le moment magnétique de l'électron, une interaction connue sous le nom de couplage spin-spin. L'énergie du système électron-proton est différente selon que les moments sont alignés ou non. Les transitions entre ces états (transitions spin-flip) se traduisent par l'émission d'un photon d'une longueur d'onde de\(\lambda = 21\) cm (dans la gamme radio). La ligne de 21 cm en spectroscopie atomique est une « empreinte » de l'hydrogène gazeux. Les astronomes exploitent cette raie spectrale pour cartographier les bras spiraux des galaxies, qui sont principalement composés d'hydrogène (Figure\(\PageIndex{4}\)).

Une spécification complète de l'état d'un électron dans un atome d'hydrogène nécessite cinq nombres quantiques : n, l, m, s et\(m_s\). Les noms, symboles et valeurs autorisées de ces nombres quantiques sont résumés dans le tableau\(\PageIndex{4}\).
| Nom | symbole | Valeurs autorisées |
|---|---|---|
| Nombre quantique principal | n | 1, 2, 3,... |
| Moment cinétique | l | 0, 1, 2,... n — 1 |
| Projection du moment angulaire | m | \(0, \pm 1, \pm 2, . . . \pm l\) |
| Spin | s | 1/2 (électrons) |
| Projection de spin | \(m_s\) | \(- 1/2, \, +1/2\) |
Notez que les nombres quantiques intrinsèques présentés dans cette section (\(s\)et\(m_s\)) sont valides pour de nombreuses particules, et pas seulement pour les électrons. Par exemple, les quarks d'un noyau atomique sont également des demi-particules de spin. Comme nous le verrons plus loin, les nombres quantiques aident à classer les particules subatomiques et à entrer dans des modèles scientifiques qui tentent d'expliquer le fonctionnement de l'univers.


