2.5 : Lentilles fines

Last updated
Save as PDF

Page ID: 189855

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Utilisez des diagrammes à rayons pour localiser et décrire l'image formée par un objectif
Utilisez l'équation de la lentille fine pour décrire et localiser l'image formée par une lentille

Les objectifs se trouvent dans une vaste gamme d'instruments optiques, allant de la simple loupe au zoom d'un appareil photo en passant par l'œil lui-même. Dans cette section, nous utilisons la loi de Snell pour explorer les propriétés des lentilles et la façon dont elles forment des images.

Le mot « lentille » vient du mot latin désignant une lentille, dont la forme est similaire à celle d'une lentille convexe. Cependant, toutes les lentilles n'ont pas la même forme. La figure\(\PageIndex{1}\) montre une variété de formes de lentilles différentes. Le vocabulaire utilisé pour décrire les lentilles est le même que celui utilisé pour les miroirs sphériques : l'axe de symétrie d'une lentille est appelé axe optique, où cet axe coupe la surface de la lentille est appelé sommet de la lentille, et ainsi de suite.

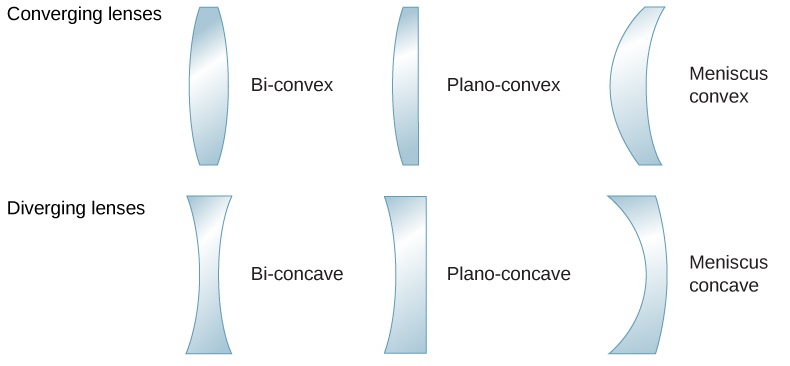
La figure montre trois lentilles convergentes et trois lentilles divergentes. Les lentilles convergentes sont : biconvexes, avec deux surfaces convexes, plano-convexes, avec une surface convexe et une fois plane et un ménisque convexe, avec une surface convexe et une surface concave, la convexe ayant un rayon de courbure plus petit. Les lentilles divergentes sont : biconcaves, avec deux surfaces concaves, plano-concaves, avec une surface concave et une fois plane et un ménisque concave, avec une surface concave et une surface convexe, la partie concave ayant un rayon de courbure plus petit. — Figure\(\PageIndex{1}\) : Différents types de lentilles : Notez qu'une lentille convergente a une « taille » plus épaisse, alors qu'une lentille divergente a une taille plus fine.

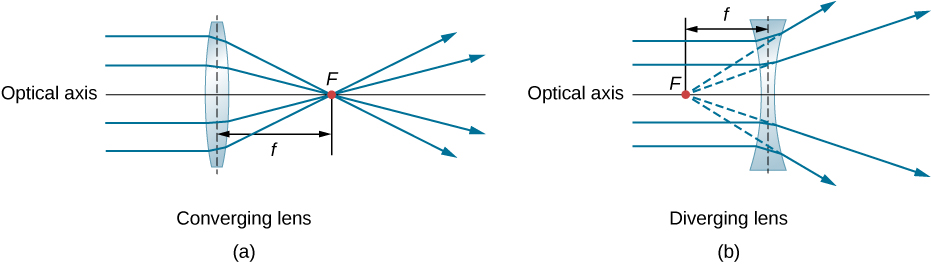
Une lentille convexe ou convergente est façonnée de telle sorte que tous les rayons lumineux qui y pénètrent parallèlement à son axe optique se croisent (ou se focalisent) en un seul point de l'axe optique sur le côté opposé de la lentille, comme indiqué sur la figure\(\PageIndex{1a}\). De même, une lentille concave ou divergente est façonnée de telle sorte que tous les rayons qui y pénètrent parallèlement à son axe optique divergent, comme indiqué dans la partie (b). Pour comprendre plus précisément comment une lentille manipule la lumière, examinez attentivement le rayon supérieur qui traverse la lentille convergente dans la partie (a). Comme l' indice de réfraction de la lentille est supérieur à celui de l'air, la loi de Snell nous indique que le rayon est courbé vers la perpendiculaire à l'interface lorsqu'il entre dans la lentille. De même, lorsque le rayon sort de la lentille, il est courbé à l'opposé de la perpendiculaire. Le même raisonnement s'applique aux lentilles divergentes, comme le montre la figure \(\PageIndex{1b}\). L'effet global est que les rayons lumineux sont courbés vers l'axe optique pour une lentille convergente et s'éloignent de l'axe optique pour les lentilles divergentes. Pour une lentille convergente, le point de croisement des rayons est le point focal F de la lentille. Pour une lentille divergente, le point d'où les rayons semblent provenir est le point focal (virtuel). La distance entre le centre de la lentille et son point focal est la distance focale f de la lentille.

La figure a montre des rayons parallèles à l'axe optique frappant une lentille biconvexe et convergeant de l'autre côté au point F. La figure b montre des rayons parallèles à l'axe optique frappant une lentille biconcave et divergeant de l'autre côté. Les rayons divergents se prolongent vers l'arrière et semblent provenir du point F situé devant la lentille. Sur les deux figures, la distance entre le centre de la lentille et le point F est désignée f. — Figure\(\PageIndex{2}\) : Les rayons lumineux entrant (a) dans une lentille convergente et (b) dans une lentille divergente, parallèlement à son axe, convergent vers son point focal F. La distance entre le centre de la lentille et le point focal est la distance focale de la lentille f. Notez que les rayons lumineux sont courbés à l'entrée et à la sortie du lentille, l'effet global étant de courber les rayons vers l' axe optique.

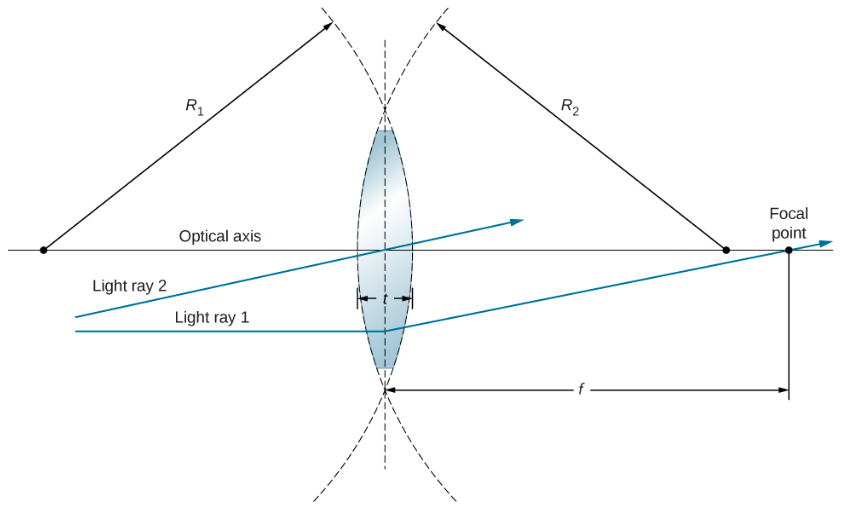
Une lentille est considérée comme mince si son épaisseur t est bien inférieure aux rayons de courbure des deux surfaces, comme le montre la figure\(\PageIndex{3}\). Dans ce cas, on peut considérer que les rayons se courbent une fois au centre de la lentille. Dans le cas illustré sur la figure, le rayon lumineux 1 est parallèle à l'axe optique, de sorte que le rayon sortant est courbé une fois au centre de la lentille et passe par le point focal. Une autre caractéristique importante des lentilles fines est que les rayons lumineux qui traversent le centre de la lentille ne sont pas déviés, comme le montre le rayon lumineux 2.

La figure montre la section transversale d'une lentille biconvexe. Les rayons de courbure des surfaces droite et gauche sont respectivement R1 et R2. L'épaisseur de la lentille est t. Le rayon lumineux 1 entre dans la lentille, dévie et traverse le point focal. Le rayon lumineux 2 traverse le centre de la lentille sans dévier. — Figure\(\PageIndex{3}\) : Dans l' approximation de la lentille mince, l'épaisseur t de la lentille est très, très inférieure aux rayons R ₁ et R ₂ de courbure des surfaces de la lentille. Les rayons lumineux sont considérés comme se courbant au centre de la lentille, tels que le rayon lumineux 1. Le rayon lumineux 2 passe par le centre de la lentille et n'est pas dévié dans l' approximation de la lentille mince.

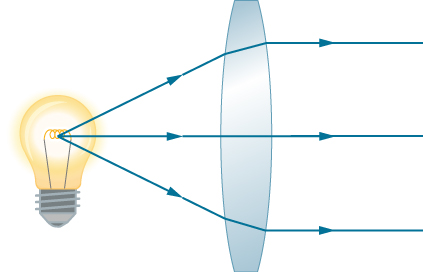
Comme indiqué dans la discussion initiale sur la loi de Snell, les trajectoires des rayons lumineux sont exactement réversibles. Cela signifie que la direction des flèches peut être inversée pour tous les rayons de la figure \(\PageIndex{2}\). Par exemple, si une source de lumière ponctuelle est placée au point focal d'une lentille convexe, comme le montre la figure \(\PageIndex{4}\), des rayons lumineux parallèles émergent de l'autre côté.

La figure montre les rayons d'une ampoule entrant dans une lentille biconvexe et émergeant de l'autre côté sous forme de rayons parallèles. — Figure\(\PageIndex{4}\) dans des verres convergents et divergents. Cette technique est utilisée dans les phares et parfois dans les feux de circulation pour produire un faisceau lumineux directionnel à partir d'une source qui émet de la lumière dans toutes les directions.

Raytracing et lentilles fines

Le ray tracing est la technique qui permet de déterminer ou de suivre (tracer) les trajectoires empruntées par les rayons lumineux. Le ray tracing pour lentilles fines est très similaire à la technique que nous avons utilisée avec les miroirs sphériques. En ce qui concerne les miroirs, le ray tracing permet de décrire avec précision le fonctionnement d'une lentille. Les règles du ray tracing pour les lentilles fines sont similaires à celles des miroirs sphériques :

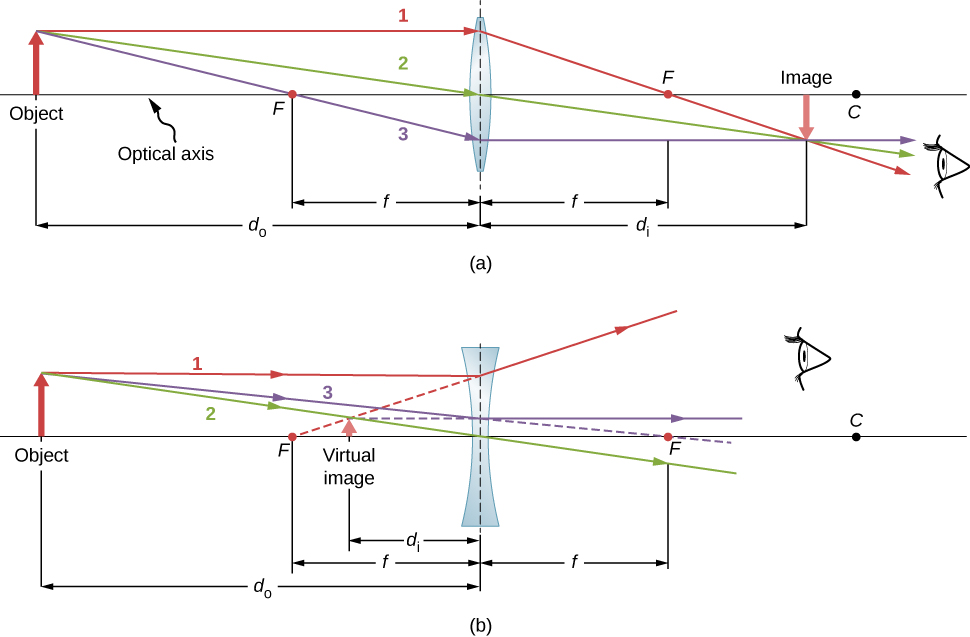
Un rayon pénétrant dans une lentille convergente parallèle à l'axe optique passe par le point focal situé de l'autre côté de la lentille (rayon 1 dans la partie (a) de la figure\(\PageIndex{4}\)). Un rayon pénétrant dans une lentille divergente parallèlement à l'axe optique sort le long de la ligne passant par le point focal situé du même côté de la lentille (rayon 1 dans la partie (b) de la figure).
Un rayon passant par le centre d'une lentille convergente ou divergente n'est pas dévié (rayon 2 dans les parties (a) et (b)).
Pour une lentille convergente, un rayon qui passe par le point focal sort de la lentille parallèlement à l'axe optique (rayon 3 dans la partie (a)). Pour une lentille divergente, un rayon qui s'approche le long de la ligne passant par le point focal du côté opposé sort de la lentille parallèlement à l'axe (rayon 3 dans la partie (b)).

La figure a montre une lentille biconvexe avec des points focaux des deux côtés. Un objet est placé sur son axe optique. Trois rayons proviennent du haut de cet objet et pénètrent dans l'objectif. Le rayon 1 est parallèle à l'axe optique. Le rayon 2 frappe le centre de l'objectif. Le rayon 3 traverse le point focal avant de pénétrer dans l'objectif. Les rayons convergent de l'autre côté pour former une image. Le rayon 1 traverse le point focal et le rayon 3 est maintenant parallèle à l'axe. La figure b montre une lentille biconcave avec des points focaux des deux côtés. Un objet est placé sur son axe optique. Trois rayons proviennent du haut de cet objet et pénètrent dans l'objectif. Le rayon 1 est parallèle à l'axe, le rayon 2 frappe le centre de la lentille et le rayon 3, s'il est étendu en ligne droite, traversera le point focal de l'autre côté de la lentille. Les trois rayons divergent de l'autre côté de la lentille. Le rayon 3 est maintenant parallèle à l'axe et l'extension arrière du rayon 1 traverse le point focal situé devant l'objectif. Les extensions arrière des trois rayons convergent pour former une image virtuelle, beaucoup plus petite que l'objet, devant l'objectif. — Figure\(\PageIndex{5}\) : Les lentilles fines ont les mêmes distances focales de chaque côté. a) Rayons lumineux parallèles pénétrant dans une lentille convergente à partir de la croix droite à son point focal situé à gauche. (b) Les rayons lumineux parallèles qui pénètrent dans une lentille divergente par la droite semblent provenir du point focal situé sur la droite.

Les lentilles fines fonctionnent très bien pour la lumière monochromatique (c'est-à-dire la lumière d'une seule longueur d'onde). Toutefois, pour la lumière contenant plusieurs longueurs d'onde (par exemple, la lumière blanche), les lentilles fonctionnent moins bien. Le problème est que, comme nous l'avons appris dans le chapitre précédent, l'indice de réfraction d'un matériau dépend de la longueur d'onde de la lumière. Ce phénomène est responsable de nombreux effets colorés, tels que les arcs-en-ciel. Malheureusement, ce phénomène entraîne également des aberrations dans les images formées par les lentilles. En particulier, comme la distance focale de la lentille dépend de l'indice de réfraction, elle dépend également de la longueur d'onde de la lumière incidente. Cela signifie que la lumière de différentes longueurs d'onde se focalise sur différents points, ce qui entraîne ce que l'on appelle des « aberrations chromatiques ». En particulier, les bords de l'image d'un objet blanc deviendront colorés et flous. Les lentilles spéciales appelées doublets sont capables de corriger les aberrations chromatiques. Un doublet est formé en collant ensemble une lentille convergente et une lentille divergente. La lentille doublet combinée produit des aberrations chromatiques considérablement réduites.

Formation d'images par lentilles fines

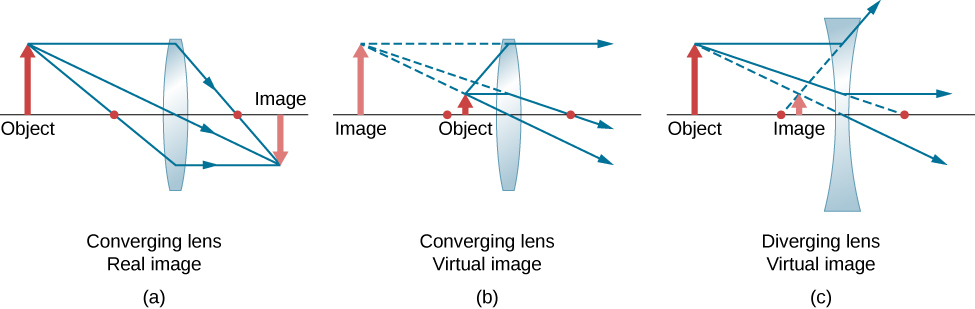
Nous utilisons le ray tracing pour étudier différents types d'images pouvant être créées par un objectif. Dans certaines circonstances, un objectif forme une image réelle, par exemple lorsqu'un projecteur projette une image sur un écran. Dans d'autres cas, l'image est une image virtuelle qui ne peut pas être projetée sur un écran. Où, par exemple, l'image est-elle formée par les lunettes ? Nous utilisons le ray tracing pour les lentilles fines afin d'illustrer la façon dont elles forment des images, puis nous développons des équations pour analyser quantitativement les propriétés des lentilles fines.

Considérez un objet à une certaine distance d'une lentille convergente, comme le montre la figure\(\PageIndex{6}\). Pour trouver l'emplacement et la taille de l'image, nous tracons les trajectoires des rayons lumineux sélectionnés provenant d'un point de l'objet, dans ce cas, de la pointe de la flèche. La figure montre trois rayons parmi de nombreux rayons qui émanent de la pointe de la flèche. Ces trois rayons peuvent être tracés en utilisant les règles de traçage de rayons données ci-dessus.

Le rayon 1 entre dans la lentille parallèlement à l'axe optique et passe par le point focal du côté opposé (règle 1).
Le rayon 2 passe par le centre de la lentille et n'est pas dévié (règle 2).
Le rayon 3 traverse le point focal pour atteindre l'objectif et en sort parallèlement à l'axe optique (règle 3).

Les trois rayons se croisent en un seul point du côté opposé de la lentille. Ainsi, l'image de la pointe de la flèche se trouve à cet endroit. Tous les rayons qui proviennent du bout de la flèche et pénètrent dans la lentille sont réfractés et se croisent au point indiqué.

Après avoir localisé l'image de la pointe de la flèche, nous avons besoin d' un autre point de l'image pour orienter l'image entière de la flèche. Nous avons choisi de localiser la base de l'image de la flèche, qui se trouve sur l'axe optique. Comme expliqué dans la section sur les miroirs sphériques, la base se trouvera sur l'axe optique juste au-dessus de l'image de la pointe de la flèche (en raison de la symétrie de haut en bas de la lentille). Ainsi, l' image s'étend sur l'axe optique jusqu'à la hauteur (négative) indiquée. Les rayons provenant d'un autre point de la flèche, tel que le milieu de la flèche, se croisent en un autre point commun, remplissant ainsi le reste de l' image.

Bien que trois rayons soient tracés sur cette figure, seuls deux sont nécessaires pour localiser un point de l'image. Il est préférable de tracer des rayons pour lesquels il existe des règles simples de traçage des rayons.

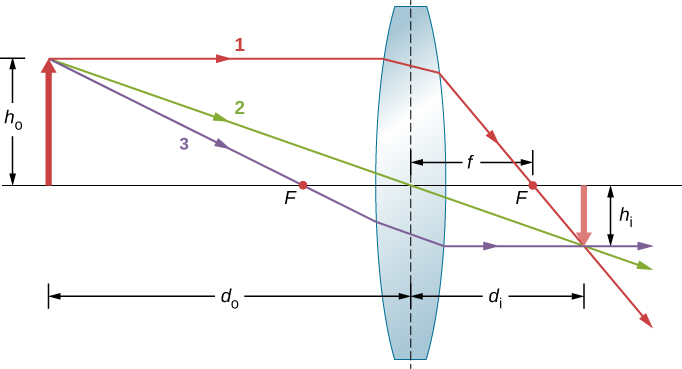
La figure montre la section transversale d'une lentille biconvexe. Trois rayons proviennent du haut d'un objet et pénètrent dans l'objectif. Le rayon 1 est parallèle à l'axe optique. Le rayon 2 traverse le centre de l'objectif. Le rayon 3 traverse le point focal situé devant l'objectif. Tous les rayons convergent de l'autre côté, en haut d'une image inversée. Le rayon 1 traverse le point focal situé derrière l'objectif. Le jour 2 n'est pas dévié. Le rayon 3 devient parallèle à l'axe optique. La distance de l'objet et la distance de l'image sont respectivement l'indice d o et l'indice d I. Les hauteurs de l'objet et de l'image sont respectivement l'indice h o et l'indice h II. La distance focale est f. — Figure\(\PageIndex{6}\) : Le ray tracing est utilisé pour localiser l'image formée par un objectif. Les rayons provenant du même point de l'objet sont tracés : les trois rayons choisis suivent chacun l'une des règles du ray tracing, de sorte que leur trajectoire est facile à déterminer. L'image est située à l'endroit où les rayons se croisent. Dans ce cas, une image réelle, qui peut être projetée sur un écran, est formée.

Plusieurs distances importantes apparaissent sur la figure. En ce qui concerne un miroir, nous définissons dodo comme étant la distance de l'objet, ou la distance entre un objet et le centre d'une lentille. La distance d'image d _i est définie comme étant la distance entre l'image et le centre d'un objectif. La hauteur de l'objet et la hauteur de l' image sont indiquées respectivement par h _o et h _i. Les images qui apparaissent debout par rapport à l'objet ont des hauteurs positives, tandis que celles qui sont inversées ont des hauteurs négatives. En utilisant les règles du ray tracing et en réalisant un dessin à l'échelle avec du papier et un crayon, comme celui de la Figure \(\PageIndex{6}\), nous pouvons décrire avec précision l'emplacement et la taille d'une image. Mais le véritable avantage du ray tracing réside dans la visualisation de la façon dont les images se forment dans diverses situations.

Rayons parallèles obliques et plan focal

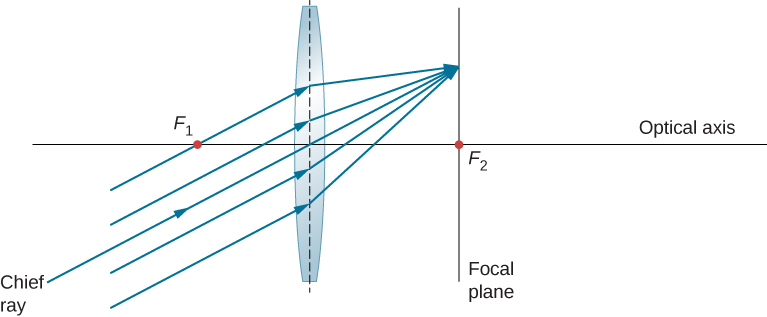
Nous avons vu que les rayons parallèles à l'axe optique sont dirigés vers le point focal d'une lentille convergente. Dans le cas d'une lentille divergente, elles sortent dans une direction telle qu'elles semblent provenir du point focal situé du côté opposé de la lentille (c'est-à-dire du côté par lequel les rayons parallèles entrent dans la lentille). Qu'arrive-t-il aux rayons parallèles qui ne sont pas parallèles à l'axe optique (Figure \(\PageIndex{7}\)) ? Dans le cas d'une lentille convergente, ces rayons ne convergent pas au point focal. Au lieu de cela, ils se rejoignent sur un autre point du plan appelé plan focal. Le plan focal contient le point focal et est perpendiculaire à l'axe optique. Comme le montre la figure, les rayons parallèles se concentrent là où le rayon passant par le centre de la lentille traverse le plan focal.

La figure montre des rayons parallèles entre eux mais pas à l'axe optique, pénétrant dans une lentille biconvexe et convergeant de l'autre côté en un point du plan focal. La section transversale du plan focal est représentée par une ligne perpendiculaire à l'axe optique et coupant celui-ci au point focal. — Figure\(\PageIndex{7}\) : Les rayons obliques parallèles se focalisent sur un point du plan focal.

Équation à lentilles fines

Le ray tracing nous permet d'obtenir une image qualitative de la formation de l'image. Pour obtenir des informations numériques, nous dérivons une paire d' équations à partir d'une analyse géométrique du ray tracing pour les lentilles fines. Ces équations, appelées équation de la lentille fine et équation du fabricant de lentilles, nous permettent d'analyser quantitativement les lentilles fines.

Considérez la lentille biconvexe épaisse illustrée sur la figure \(\PageIndex{8}\). L'indice de réfraction du milieu environnant est n ₁ (si la lentille est dans l'air, alors\(n_1=1.00\)) et celui de la lentille est\(n_2\). Les rayons de courbure des deux côtés sont\(R_1\) et\(R_2\). Nous souhaitons trouver une relation entre la distance de l'objet\(d_o\), la distance\(d_i\) de l'image et les paramètres de l'objectif.

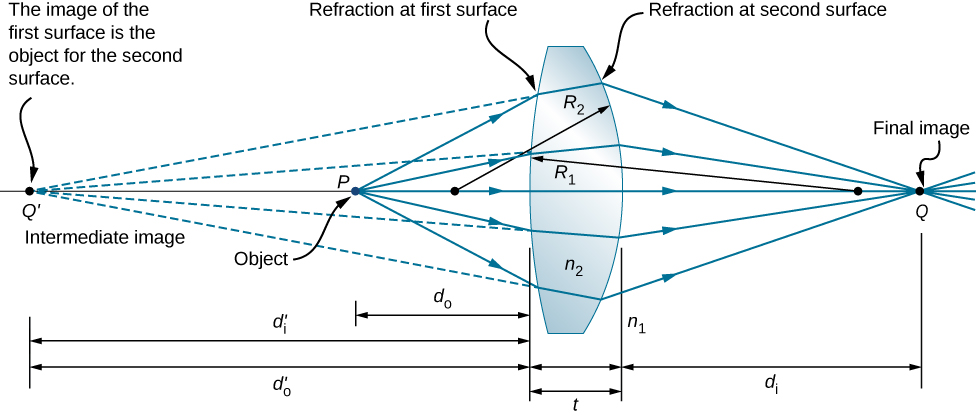
La figure montre une lentille biconvexe avec une épaisseur t et des rayons de courbure des surfaces avant et arrière R1 et R2 respectivement. Les indices de réfraction de l'air et de la lentille sont respectivement n1 et n2. Les rayons provenant d'un objet situé au point P de l'axe optique situé devant la lentille frappent la première surface et sont réfractés à l'intérieur de la lentille. Les extensions arrière des rayons réfractés convergent au point Q prime pour former une image intermédiaire. Q prime se trouve devant la lentille, plus loin de celle-ci que P. Les rayons à l'intérieur de la lentille se réfractent davantage lorsqu'ils émergent de la seconde surface. Ils convergent au point Q derrière l'objectif pour former l'image finale. Les distances entre l'objectif et l'objet, l'image intermédiaire et l'image finale sont respectivement d0, d0 prime et di. d0 prime est également identique à di prime. — Figure\(\PageIndex{8}\) permettant de calculer l' équation du fabricant de lentilles. Ici,\(t\) c'est l'épaisseur de la lentille, n ₁ est l'indice de réfraction du milieu extérieur, et\(n_2\) est l' indice de réfraction de la lentille. Nous prenons la limite de\(t→0\) pour obtenir la formule d'une lentille fine.

Pour dériver l'équation de la lentille mince, nous considérons l'image formée par la première surface de réfraction (c'est-à-dire la surface gauche), puis nous utilisons cette image comme objet pour la deuxième surface de réfraction. Sur la figure, l'image de la première surface de réfraction est\(Q′\) formée en étendant vers l'arrière les rayons provenant de l'intérieur de la lentille (ces rayons résultent de la réfraction au niveau de la première surface). Ceci est illustré par les lignes pointillées sur la figure. Notez que cette image est virtuelle car aucun rayon ne passe réellement par le point Q′. Pour trouver la distance d'image\(d′_i\) correspondant à l'image Q′, nous utilisons l'équation 2.4.9. Dans ce cas, la distance de l'objet est\(d_o\), la distance de l'image est d' idi′ et le rayon de courbure est\(R_1\). En les insérant dans la relation dérivée précédemment pour la réfraction aux surfaces des courbes, on obtient

\ [\ dfrac {n_1} {d_o} + \ dfrac {n_2} {d′_i} = \ dfrac {n_2−n_1} {R_1}. \ label {51} \]

L'image est virtuelle et du même côté que l'objet, donc d _i ′<0 et d _o >0. La première surface est convexe vers l'objet, donc\(R_1>0\).

Pour déterminer la distance entre l'objet\(Q\) formé par la réfraction à partir de la deuxième interface, notez que les rôles des indices de réfraction n ₁ et n ₂ sont inversés dans l'équation 2.4.9. Dans la figure\(\PageIndex{8}\), les rayons proviennent du milieu d' indice\(n_2\), alors que dans la figure 2.4.3, les rayons proviennent du milieu d'indice \(n_1\). Il faut donc échanger n ₁ et n ₂ dans l'équation 2.4.9. De plus, en consultant à nouveau la figure\(\PageIndex{8}\), nous voyons que la distance de l'objet est\(d′_o\) et la distance de l'image est \(d_i\). Le rayon de courbure est R ₂ En insérant ces grandeurs dans l'équation 2.4.9, on obtient

\ [\ dfrac {n_2} {d′_o} + \ dfrac {n_1} {d_i} = \ dfrac {n_1−n_2} {R_2}. \ label {eq51} \]

L'image est réelle et se trouve du côté opposé à l'objet, donc \(d_i>0\) et\(d_o′>0\). La deuxième surface est convexe à l'opposé de l'objet, donc\(R_2<0\). L'équation \ ref {eq51} peut être simplifiée en notant que

\[d′_o=|d′_i|+t, \nonumber \]

où nous avons pris la valeur absolue parce que\(d′_i\) c'est un nombre négatif, alors que les deux\(d′_o\) et\(t\) sont positifs. Nous pouvons nous passer de la valeur absolue si nous nions\(d′_i\), ce qui donne

\[ d′_o=−d′_i+td. \nonumber \]

L'insertion de ceci dans l'équation \ ref {eq51} donne

\ [\ dfrac {n_2} {−d′_i+t} + \ dfrac {n_1} {d_i} = \ dfrac {n_1−n_2} {R_2}. \ label {eq52} \]

La somme des équations \ ref {eq51} et \ ref {eq52} donne

\ [\ dfrac {n_1} {d_o} + \ dfrac {n_1} {d_i} + \ dfrac {n_2} {d′_i} + \ dfrac {n_2} {−d′_i+t} = (n_2−n_1) \ left (\ dfrac {1} {R_1} − \ dfrac {1} {R_2} \ à droite). \ label {eq54} \]

Dans l'approximation de la lentille mince, nous supposons que l'objectif est très fin par rapport à la distance de la première image, ou\(t \ll d′_i\) (ou, de manière équivalente,\(t \ll R_1\) et\(t \ll R_2\)). Dans ce cas, les troisième et quatrième termes sur le côté gauche de l'équation \ ref {eq54} sont annulés, ce qui nous laisse

\ [\ dfrac {n_1} {d_o} + \ dfrac {n_1} {d_i} = (n_2−n_1) \ left (\ dfrac {1} {R_1} − \ dfrac {1} {R_2} \ droite). \ aucun numéro \]

Diviser par nous\(n_1\) donne enfin

\ [\ dfrac {1} {d_o} + \ dfrac {1} {d_i} = \ left (\ dfrac {n_2} {n_1} −1} −1 \ right) \ left (\ dfrac {1} {R_1} − \ dfrac {1} {R_2} \ droite). \ label {eq58} \]

Le côté gauche ressemble étrangement à l'équation du miroir que nous avons dérivée ci-dessus pour les miroirs sphériques. Comme pour les miroirs sphériques, nous pouvons utiliser le ray tracing et la géométrie pour montrer que, pour une lentille fine,

\ [ \ underbrace {\ dfrac {1} {d_o} + \ dfrac {1} {d_i} = \ dfrac {1} {f}} _ { \ text {équation de lentille fine}} \ label {équation de lentille fine} \]

où\(f\) est la distance focale de la lentille fine (cette dérivation est laissée à titre d'exercice). Il s'agit de l' équation de la lentille fine. La distance focale d'une lentille fine est la même à gauche et à droite de la lentille. La combinaison des équations \ ref {équation à lentille mince} et \ ref {eq58} donne

\ [\ underbrace {\ dfrac {1} {f} = \ left (\ dfrac {n_2} {n_1} −1 \ right) \ left (\ dfrac {1} {R_1} − \ dfrac {1} {R_2} \ right)} _ {\ text { équation de l'objectif}} \ label {lensmaker} \]

ce que l'on appelle l'équation du fabricant de lentilles. Il montre que la distance focale d'une lentille mince dépend uniquement des rayons de courbure et de l'indice de réfraction de la lentille et de celui du milieu environnant. Pour une lentille en l'air\(n_2≡n\),\(n_1=1.0\) et donc l'équation du fabricant de l'objectif se réduit à

\ [\ dfrac {1} {f} = (n−1) \ left (\ dfrac {1} {R_1} − \ dfrac {1} {R_2} \ droite). \ aucun numéro \]

Signer les conventions relatives aux lentilles

Pour utiliser correctement l'équation de la lentille fine, les conventions de signes suivantes doivent être respectées :

\(d_i\)est positive si l'image se trouve du côté opposé à l' objet (image réelle) ; dans le cas contraire, elle\(d_i\) est négative (image virtuelle).
\(f\)est positif pour une lentille convergente et négatif pour une lentille divergente.
\(R\)est positif pour une surface convexe vers l'objet et négatif pour une surface concave vers l'objet.

Agrandissement

En utilisant un objet de taille finie sur l'axe optique et en traçant des rayons, vous pouvez montrer que le grossissement\(m\) d'une image est

\[m \equiv \dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o} \label{mag} \]

(où les trois lignes signifient « est défini comme »). Il s'agit exactement de la même équation que celle que nous avons obtenue pour les rétroviseurs (voir Équation 2.3.15). Si\(m>0\), alors l'image a la même orientation verticale que l'objet (appelée image « verticale »). Si m<0, l'image a l'orientation verticale opposée à celle de l'objet (appelée image « inversée »).

Utilisation de l'équation de la lentille fine

L'équation des lentilles fines et celle du fabricant de lentilles sont largement applicables aux situations impliquant des lentilles fines. Nous explorons de nombreuses fonctionnalités de la formation d'images dans les exemples suivants.

Prenons l'exemple d'une fine lentille convergente. Où se forme l'image et quel type d'image se forme lorsque l'objet s'approche de l'objectif depuis l' infini ? Cela peut être observé en utilisant l'équation de la lentille fine pour une distance focale donnée afin de tracer la distance de l'image en fonction de la distance de l'objet. En d'autres termes, nous tracons

\[d_i=\left(\dfrac{1}{f}−\dfrac{1}{d_o}\right)^{−1} \nonumber \]

pour une valeur donnée de\(f\). Pour\(f=1\,cm\), le résultat est illustré dans la figure\(\PageIndex{9a}\).

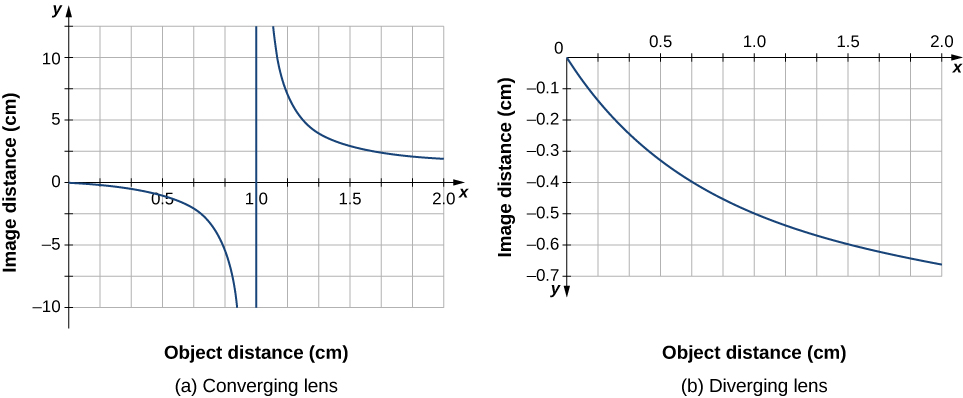
La figure a montre le graphique de y égal à x sur x - 1. La figure b montre le graphe de y égal à x sur −x-1. Dans les deux graphes, l'axe y est appelé distance de l'image et l'axe x est intitulé distance de l'objet. — Figure\(\PageIndex{9}\) : (a) Distance d'image pour une lentille convergente fine avec f = 1,0 cm en fonction de la distance de l'objet. (b) Même chose mais pour une lentille divergente avec f = −1,0 cm.

Un objet bien plus éloigné que la distance focale f de l' objectif devrait produire une image proche du plan focal, car le second terme sur le côté droit de l'équation ci-dessus devient négligeable par rapport au premier terme, c'est ce que nous avons fait\(d_i≈f\). Cela se voit sur le diagramme de la partie (a) de la figure, qui montre que la distance de l'image se rapproche de façon asymptotique de la distance focale de 1 cm pour des distances d'objet plus importantes. Lorsque l'objet s'approche du plan focal, la distance de l'image diverge vers l'infini positif. Cela est normal car un objet situé sur le plan focal produit des rayons parallèles qui forment une image à l'infini (c'est-à-dire très loin de l'objectif). Lorsque l'objet est plus éloigné que la distance focale de l'objectif, la distance de l' image est positive, donc l'image est réelle, du côté opposé de l'objectif à l'objet, et inversée (car \(m=−d_i/d_o\) via l'équation \ ref {mag}). Lorsque l'objet est plus proche que la distance focale de l'objectif, la distance de l'image devient négative, ce qui signifie que l'image est virtuelle, du même côté de l'objectif que l'objet, et verticale.

Pour une lentille divergente mince de distance focale\(f =−1.0\, cm\), un diagramme similaire de la distance de l'image par rapport à la distance de l'objet est illustré sur la figure\(\PageIndex{10b}\). Dans ce cas, la distance de l'image est négative pour toutes les distances positives de l'objet, ce qui signifie que l' image est virtuelle, du même côté de l'objectif que l'objet, et verticale. Ces caractéristiques peuvent également être observées par des diagrammes de traçage de rayons (Figure\(\PageIndex{10}\)).

La figure a montre une lentille biconvexe, un objet dont la distance focale est supérieure à la distance focale et une image inversée derrière l'objectif. La figure b montre une lentille biconvexe, un objet plus proche que la distance focale et une image verticale devant l'objectif, plus éloignée que le point focal. La figure c montre un objectif biconcave, un objet dont la distance focale est supérieure à la distance focale et une image verticale devant l'objectif, entre l'objectif et le point focal. — Figure\(\PageIndex{10}\) : Les points rouges indiquent les points focaux des verres. (a) Une image inversée réelle formée à partir d'un objet situé plus loin que la distance focale d'une lentille convergente. (b) Une image verticale virtuelle formée à partir d'un objet situé à moins d'une distance focale de l'objectif. (c) Une image verticale virtuelle formée à partir d'un objet dont la distance focale est supérieure à la distance focale d'une lentille divergente.

Pour voir un exemple concret d'images verticales et inversées, regardez la Figure\(\PageIndex{11}\), qui montre des images formées par des lentilles convergentes lorsque l'objet (le visage de la personne dans ce cas) est placé à différentes distances de l'objectif. Dans la partie (a) de la figure, le visage de la personne se trouve à plus d'une distance focale de l' objectif, de sorte que l'image est inversée. Dans la partie (b), le visage de la personne se trouve à moins d'une distance focale de l'objectif, de sorte que l'image est droite.

La figure a montre un homme tenant un objectif, sur lequel est visible une minuscule image inversée de son visage. La figure b montre un homme tenant une lentille dans laquelle est visible une image agrandie de son œil. — Figure\(\PageIndex{11}\) : (a) Lorsqu'une lentille convergente est maintenue à plus d'une distance focale du visage de l'homme, une image inversée se forme. Notez que l'image est nette, mais pas le visage, car l'image est beaucoup plus proche de l'appareil photo qui prend cette photo que du visage. (b) Une image verticale du visage de l'homme est produite lorsqu'une lentille convergente est maintenue à moins d'une distance focale de son visage. (crédit a : modification de l'œuvre par « DaLongman » /Flickr ; crédit b : modification de l'œuvre par Casey Fleser)

Parcourez les exemples suivants pour mieux comprendre le fonctionnement des lentilles fines.

STRATÉGIE DE RÉSOLUTION DE PROBLÈMES : LENTILLES

Étape 1. Déterminez si le traçage des rayons, l'équation de la lentille mince ou les deux seraient utiles. Même si le ray tracing n'est pas utilisé, un croquis minutieux est toujours très utile. Écrivez des symboles et des valeurs sur l' esquisse.
Étape 2. Déterminez ce qui doit être déterminé dans le problème (identifier les inconnues).
Étape 3. Dressez une liste de ce qui est indiqué ou peut être déduit du problème (identifier les éléments connus).
Étape 4. Si le ray tracing est requis, utilisez les règles de ray tracing répertoriées au début de cette section.
Étape 5. La plupart des problèmes quantitatifs nécessitent l'utilisation de l'équation de la lentille fine et/ou de l'équation du fabricant de lentilles. Résolvez-les pour les inconnues et insérez les quantités données ou utilisez les deux ensemble pour trouver deux inconnues.
Étape 7. Vérifiez si la réponse est raisonnable. Les signes sont-ils corrects ? L'esquisse ou le ray tracing est-il cohérent avec le calcul ?

Exemple\(\PageIndex{1}\) : Utilisation de l'équation du fabricant de lentilles

Déterminez le rayon de courbure d'une lentille biconcave polie symétriquement à partir d'un verre dont l'indice de réfraction est de 1,55 de manière à ce que sa distance focale dans l'air soit de 20 cm (pour une lentille biconcave, les deux surfaces ont le même rayon de courbure).

Stratégie

Utilisez la forme à lentille fine de l'équation du fabricant de lentilles :

\ [\ dfrac {1} {f} = \ left (\ dfrac {n_2} {n_1} −1 \ right) \ left (\ dfrac {1} {R_1} − \ dfrac {1} {R_2} \ right) \ nonnumber \]

où\(R_1<0\) et\(R_2>0\). Puisque nous fabriquons une lentille biconcave symétrique, nous avons\(|R_1|=|R_2|\).

Solution

Nous pouvons déterminer le rayon\(R\) de courbure à partir de

\ [\ dfrac {1} {f} = \ left (\ dfrac {n_2} {n_1} −1 \ right) \ left (\ dfrac {−2} {R} \ right). \ aucun numéro \]

Résoudre\(R\) et insérer\(f=−20\,cm\)\(n_2=1.55\), et \(n_1=1.00\) donne

\ [\ begin {align} R &=−2f \ left (\ dfrac {n_2} {n_1} −1 \ right) \ nonnumber \ \ [4pt] &=−2 (−20 \, cm) \ left (\ dfrac {1,55} {1,00} −1 \ right) \ nonnumber \ \ [4pt] &= 22 \, cm. \ nonumber \ end {align} \ nonumber \]

Exemple\(\PageIndex{2}\) : lentille convergente et différentes distances entre objets

Trouvez l'emplacement, l'orientation et le grossissement de l'image pour un objet de 3,0 cm de haut à chacune des positions suivantes devant une lentille convexe d'une distance focale de 10,0 cm. (a) \(d_o=50.0\,cm\), (b)\(d_o=5.00\,cm\) et (c) \ (d_o=20,0 \, cm \).

Stratégie

Nous commençons par l'équation de la lentille fine (Équation \ ref { équation de la lentille mince})

\[\dfrac{1}{d_i}+\dfrac{1}{d_o}=\dfrac{1}{f}. \nonumber \]

Résolvez ce problème pour la distance de l'image\(d_i\) et insérez la distance d'objet et la distance focale données.

Solution

a. Pour\(d_o=50\, cm\) et\(f=+10\, cm\), cela donne

\ [\ begin {align} d_i &= \ left (\ dfrac {1} {f} − \ dfrac {1} {d_o} \ right) ^ {−1} \ nonumber \ \ [4pt] &= \ left (\ dfrac {1} {10,0 \, cm} − \ dfrac {1} {50,0 cm} \ droite) ^ {−1} \ nonnumber \ \ [4pt] &=12,5 \, cm \ nonumber \ end {align} \ nonnumber \]

L'image est positive, donc l'image est réelle, se trouve sur le côté opposé de l'objectif par rapport à l'objet et à 12,6 cm de l'objectif. Pour connaître le grossissement et l'orientation de l'image, utilisez

\ [\ begin {align} m &=− \ dfrac {d_i} {d_o} \ nonumber \ \ [4 points] &=− \ dfrac {12,5 \, cm} {50,0 \, cm} \ nonnumber \ \ [4 points] &=−0,250. \ nonumber \ end {align} \ nonumber \]

Le grossissement négatif signifie que l'image est inversée. Depuis\(|m|<1\), l'image est plus petite que l'objet. La taille de l'image est donnée par

\ [\ begin {align} |h_i| &=|m|h_o \ nonumber \ \ [4 points] & =( 0,250) (3,0 \, cm) \ nonnumber \ \ [4 points] &=0,75 \, cm \ nonnumber \ end {align} \ nonnumber \]

b. Pour\(d_o=5.00\,cm\) et\(f=+10.0\,cm\)

\ [\ begin {align} d_i&= \ left (\ dfrac {1} {f} − \ dfrac {1} {d_o} \ right) ^ {−1} \ nonumber \ \ [4pt] &= \ left (\ dfrac {1} {10,0 \, cm} − \ dfrac {1} {5,00 \, cm} \ droite) ^ {−1} \ nonumber \ \ [4pt] &=−10,0 \, cm \ nonnumber \ end {align} \ nonnumber \]

La distance de l'image étant négative, l'image est virtuelle, elle se trouve du même côté de l'objectif que l'objet et se trouve à 10 cm de l' objectif. Le grossissement et l'orientation de l'image sont obtenus à partir de

\ [\ begin {align} m &=− \ dfrac {d_i} {d_o} \ nonumber \ \ [4 points] &=− \ dfrac {−10,0 \, cm} {5,00 \, cm} \ nonnumber \ \ [4 points] &=+2,00. \ nonumber \ end {align} \ nonumber \]

Le grossissement positif signifie que l'image est verticale (c'est-à-dire qu'elle a la même orientation que l'objet). Depuis \(|m|>0\), l'image est plus grande que l'objet. La taille de l' image est

\ [\ begin {align} |h_i|&=|m|h_o \ nonumber \ \ [4 points] & =( 2,00) (3,0 \, cm) \ nonnumber \ \ [4 points] &=6,0 \, cm. \ nonumber \ end {align} \ nonumber \]

c. Pour\(d_o=20\,cm\) et\(f=+10cm\)

\ [\ begin {align} d_i &= \ left (\ dfrac {1} {f} − \ dfrac {1} {d_o} \ right) ^ {−1} \ nonumber \ \ [4pt] &= \ left (\ dfrac {1} {10,0 \, cm} − \ dfrac {1} {20,0 \, cm} \ right) ^ −1} \ nonumber \ \ [4pt] &=20,0 \, cm \ nonnumber \ end {align} \ nonnumber \]

La distance de l'image est positive, donc l'image est réelle, se trouve du côté opposé de l'objectif par rapport à l'objet et se trouve à 20,0 cm de l' objectif. Le grossissement est

\ [\ begin {align} m &=− \ dfrac {d_i} {d_o} \ nonumber \ \ [4 points] &=− \ dfrac {20,0 \, cm} {20,0 \, cm} \ nonnumber \ \ [4 points] &=−1,00. \ nonumber \ end {align} \ nonumber \]

Le grossissement négatif signifie que l'image est inversée. Depuis\(|m|=1\), l'image a la même taille que l'objet.

Pour résoudre des problèmes d'optique géométrique, nous avons souvent besoin de combiner le ray tracing et les équations de l'objectif. L'exemple suivant illustre cette approche.

Exemple\(\PageIndex{3}\) : Choix de la distance focale et du type d'objectif

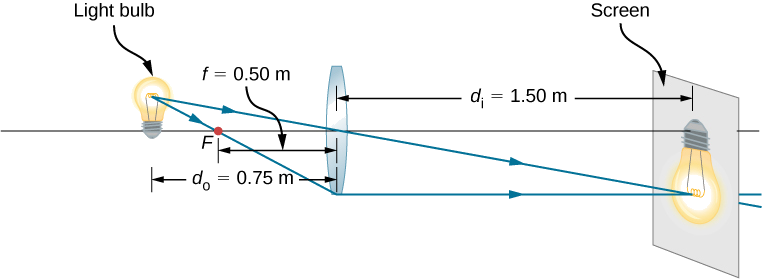
Pour projeter l'image d'une ampoule sur un écran à 1,50 m de distance, vous devez choisir le type d'objectif à utiliser (convergent ou divergent) et sa distance focale (Figure\(\PageIndex{12}\)). La distance entre l'objectif et l'ampoule est fixée à 0,75 m. De plus, quels sont le grossissement et l'orientation de l'image ?

La figure montre une lentille biconvexe d'une distance focale de 0,5 mètre et une ampoule placée à 0,75 mètre devant elle. Une image inversée de l'ampoule est formée sur un écran placé à 1,5 mètre derrière l'objectif. — Figure\(\PageIndex{12}\) : Une ampoule placée à 0,75 m d'un objectif ayant une distance focale de 0,50 m produit une image réelle sur un écran, comme indiqué dans l'exemple. Le ray tracing permet de prédire l' emplacement et la taille de l'image.

Stratégie

L'image doit être réelle, vous choisissez donc d'utiliser un objectif convergent. La distance focale peut être déterminée en utilisant l'équation de la lentille fine et en résolvant la distance focale. La distance de l'objet est \(d_o=0.75\,m\) et la distance de l'image est\(d_i=1.5\,m\).

Solution

Résolvez la distance focale de l'objectif fin et insérez les distances souhaitées entre l'objet et l'image :

\ [\ begin {align} \ dfrac {1} {d_o} + \ dfrac {1} {d_i} &= \ dfrac {1} {f} \ nonumber \ \ [4pt] f &= \ left (\ dfrac {1} {d_o} + \ dfrac {1} {d_i} \ right) ^ {−1} \ nonnumber \ \ [4pt] &= \ left (\ dfrac {1} {0,75 \, m} + \ dfrac {1} {1,5 \, m} \ right) ^ {−1} \ nonnumber \\[4pt] &= 0.50 \, m \nonumber \end{align} \nonumber \]

Le grossissement est

\ [\ begin {align} m &=− \ dfrac {d_i} {d_o} \ nonumber \ \ [4 points] &= − \ dfrac {1,5 \, m} {0,75 \, m} \ nonnumber \ \ [4 points] &=−2,0. \ nonumber \ end {align} \ nonumber \]

L'importance

Le signe moins pour le grossissement signifie que l'image est inversée. La distance focale est positive, comme prévu pour une lentille convergente. Le ray tracing peut être utilisé pour vérifier le calcul (Figure\(\PageIndex{12}\)). Comme prévu, l'image est inversée, est réelle et est plus grande que l'objet.