Skip to main content
Global

2.4 : Images formées par réfraction

  1. Last updated
  2. Save as PDF
  • Page ID
    189842

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Décrire la formation d'images par une seule surface de réfraction
    • Déterminez l'emplacement d'une image et calculez ses propriétés à l'aide d'un diagramme à rayons
    • Déterminez l'emplacement d'une image et calculez ses propriétés à l'aide de l'équation pour une surface de réfraction unique

    Lorsque les rayons lumineux se propagent d'un milieu à un autre, ils subissent une réfraction, c'est-à-dire lorsque les ondes lumineuses sont courbées à l'interface entre deux milieux. La surface réfractante peut former une image de la même manière qu'une surface réfléchissante, sauf que la loi de réfraction (loi de Snell) est au cœur du processus et non la loi de réflexion.

    Réfraction au niveau d'une interface plane—Profondeur apparente

    Si vous regardez une tige droite partiellement immergée dans l'eau, elle semble se plier à la surface. Cet effet curieux s'explique par le fait que l'image de la canne à l'intérieur de l'eau se forme un peu plus près de la surface que la position réelle de la tige, de sorte qu'elle ne correspond pas à la partie de la tige qui se trouve au-dessus de l'eau. Le même phénomène explique pourquoi un poisson dans l'eau semble être plus proche de la surface qu'il ne l'est réellement.

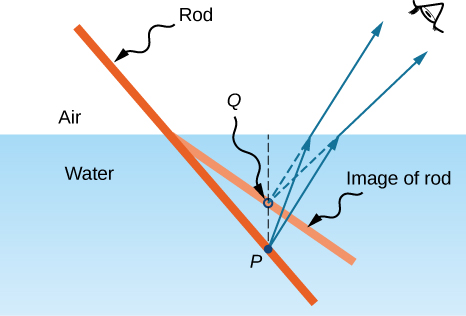
    La figure représente la vue latérale d'une canne trempée dans l'eau. Une image plus claire de la tige est représentée de manière à donner l'impression que la tige est courbée à la jonction de l'air et de l'eau. Le point P se trouve sur la tige et le point Q est sur l'image de la tige. Une ligne pointillée PQ est représentée perpendiculairement à la surface de l'eau. Deux rayons proviennent de P, remontent jusqu'à la surface de l'eau, se courbent en biais et atteignent l'œil de l'observateur. Les extensions arrières des rayons incurvés semblent provenir du point Q.
    Figure\(\PageIndex{1}\) : Flexion d'une tige à l'interface eau-air. Le point de\(P\) la tige semble se trouver au point\(Q\), où se forme l'image du point P en raison de la réfraction à l'interface air-eau.

    Pour étudier la formation d'images résultant de la réfraction, posez-vous les questions suivantes :

    1. Qu'arrive-t-il aux rayons de lumière lorsqu'ils pénètrent ou traversent un autre milieu ?
    2. Les rayons réfractés provenant d'un point unique se rencontrent-ils à un moment donné ou divergeent-ils les uns des autres ?

    Concrètement, nous considérons un système simple composé de deux supports séparés par une interface plane (Figure\(\PageIndex{2}\)). L'objet se trouve dans un milieu et l'observateur dans l'autre. Par exemple, lorsque vous observez un poisson vu au-dessus de la surface de l'eau, le poisson se trouve dans le milieu 1 (l'eau) avec un indice de réfraction de 1,33, et votre œil est dans le milieu 2 (l'air) avec un indice de réfraction de 1,00, et la surface de l'eau est l'interface. La profondeur que vous « voyez » est la hauteur de l'image\(h_i\) et est appelée profondeur apparente. La profondeur réelle du poisson est la hauteur de l'objet\(h_o\).

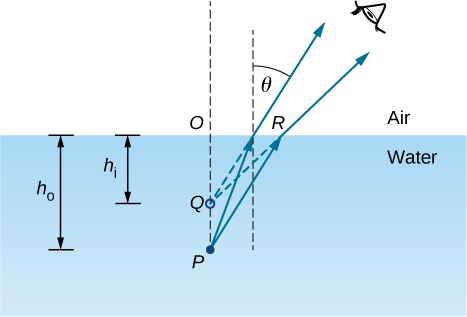
    La figure montre la vue latérale d'une certaine quantité d'eau. Le point P se trouve à l'intérieur. Deux rayons partent du point P, se courbent à la surface de l'eau et atteignent l'œil de l'observateur. Les extensions arrières de ces rayons réfractés se croisent au point Q. PQ est perpendiculaire à la surface de l'eau et l'intersecte au point O. La distance OP est notée h indice o et la distance OQ est notée h indice i. L'angle formé par le rayon réfracté avec une droite perpendiculaire à la surface de l'eau est étiqueté thêta.
    Figure\(\PageIndex{2}\) : Profondeur apparente due à la réfraction. L'objet réel au point P crée une image au point Q. L'image n'étant pas à la même profondeur que l'objet, l'observateur voit l'image à une « profondeur apparente ».

    La profondeur apparente h i dépend de l'angle sous lequel vous visualisez l'image. Pour une vue de dessus (vue dite « normale »), nous pouvons estimer que l'angle\(θ\) de réfraction est petit et le remplacer\(\sin θ\) dans la loi de Snell par\(\tan θ\). Avec cette approximation, vous pouvez utiliser les triangles\(ΔOPR\) et\(ΔOQR\) montrer que la profondeur apparente est donnée par

    \[h_i= \left(\dfrac{n_2}{n_1}\right)h_o. \nonumber \]

    La dérivation de ce résultat est laissée à titre d'exercice. Ainsi, un poisson apparaît aux 3/4 de la profondeur réelle lorsqu'il est vu de dessus.

    Réfraction à une interface sphérique

    Les formes sphériques jouent un rôle important en optique, principalement parce que les formes sphériques de haute qualité sont beaucoup plus faciles à fabriquer que les autres surfaces incurvées. Pour étudier la réfraction sur une seule surface sphérique, nous supposons que le milieu ayant la surface sphérique à une extrémité continue indéfiniment (un milieu « semi-infini »).

    Réfraction sur une surface convexe

    Considérons une source de lumière ponctuelle au point P devant une surface convexe en verre (Figure\(\PageIndex{3}\)). \(R\)Soit le rayon de courbure, n 1 l'indice de réfraction du milieu dans lequel se trouve le point objet P, et n 2 l'indice de réfraction du milieu à surface sphérique. Nous voulons savoir ce qui se passe à la suite de la réfraction à cette interface.

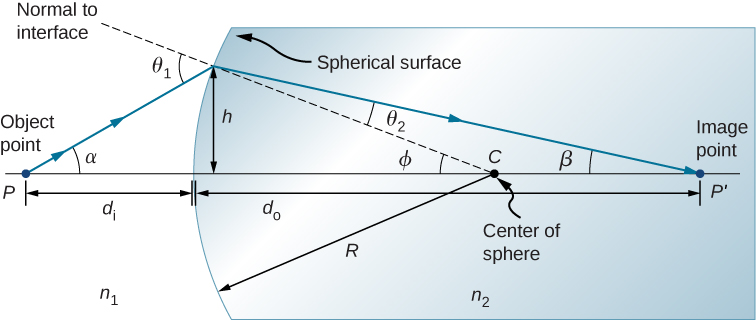
    La figure montre une section d'une sphère. L'indice de réfraction de l'air est un indice 1 et celui de la sphère est un indice 2. Le centre de la sphère est C et le rayon est R. Un rayon provenant du point P sur l'axe optique à l'extérieur de la sphère frappe la surface convexe de la sphère et est réfracté à l'intérieur de celle-ci. Il coupe l'axe au point P prime de la sphère, de l'autre côté du centre. Une ligne pointillée étiquetée perpendiculairement à l'interface relie le centre de la sphère au point d'incidence. Il fait un angle phi avec l'axe optique. Les rayons incidents et réfractés forment des angles alpha et bêta respectivement avec l'axe optique et des angles thêta 1 et thêta 2 respectivement avec la normale à l'interface.
    Figure\(\PageIndex{3}\) : Réfraction sur une surface convexe (\(n_2>n_1\)).

    En raison de la symétrie mise en jeu, il suffit d'examiner les rayons dans un seul plan. La figure montre un rayon de lumière qui commence au point de l'objet\(P\), se réfracte à l'interface et traverse le point de l'image\(P′\). Nous dérivons une formule reliant la distance de l'objet\(d_o\), la distance\(d_i\) de l'image et le rayon de courbure\(R\).

    L'application de la loi de Snell au rayon émanant du point\(P\) donne

    \[n_1\sin θ_1=n_2 \sin θ_2. \nonumber \]

    Dans le cadre de l'approximation des petits

    \[\sin θ≈θ, \nonumber \]

    La loi de Snell prend alors la forme

    \[n_1θ_1≈n_2θ_2. \label{eq8} \]

    À partir de la géométrie de la figure\(\PageIndex{3}\), nous voyons que

    \[θ_1=α+ϕ, \nonumber \]

    \[θ_2=ϕ−β. \nonumber \]

    L'insertion des deux expressions dans l'équation \ ref {eq8} donne

    \[n_1(α+ϕ)≈n_2(ϕ−β). \label{eq10} \]

    À l'aide de la figure\(\PageIndex{3}\), nous calculons la tangente des angles\(α\)\(β\), et\(ϕ\) :

    • \(\tan α≈\dfrac{h}{d_o}\)
    • \(\tan β≈\dfrac{h}{d_i}\)
    • \(\tan ϕ≈\dfrac{h}{R}\)

    Encore une fois, en utilisant l'approximation du petit angle, nous constatons que\(\tan θ≈ θ\), de sorte que les relations ci-dessus deviennent

    • \(α≈\dfrac{h}{d_o}\)
    • \(~β≈\dfrac{h}{d_i}\)
    • \(~ϕ≈\dfrac{h}{R}.\)

    Mettre ces angles dans l'équation \ ref {eq10} donne

    \[n_1\left(\dfrac{h}{d_o}+\dfrac{h}{R}\right)=n_2 \left(\dfrac{h}{R}−\dfrac{h}{d_i}\right). \nonumber \]

    Nous pouvons l'écrire plus facilement en tant que

    \[\dfrac{n_1}{d_o}+\dfrac{n_2}{d_i}=\dfrac{n_2−n_1}{R}. \label{eq20} \]

    Si l'objet est placé à un point spécial appelé premier foyer, ou foyer de l'objet\(F_1\), l'image est formée à l'infini, comme le montre la figure\(\PageIndex{4a}\).

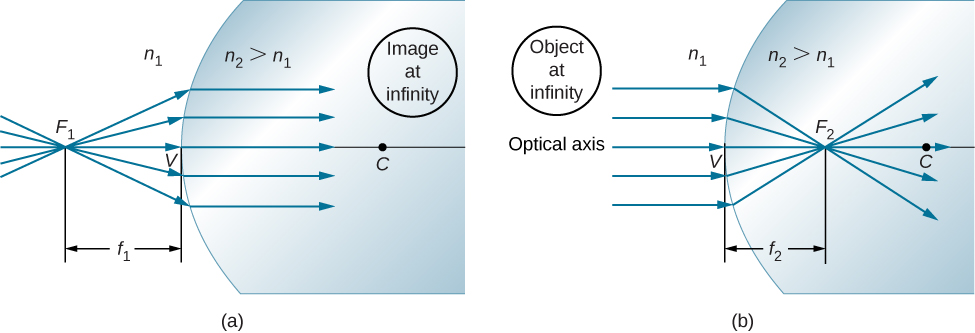
    La figure a montre une section d'une sphère et un point F1 à l'extérieur de celle-ci, sur l'axe optique. Les rayons provenant de F1 frappent la surface convexe et sont réfractés dans la sphère sous forme de rayons parallèles. La distance de F1 par rapport à la surface est de l'indice f 1. La figure b montre des rayons parallèles à l'axe optique frappant la surface convexe et se réfractant. Ils convergent au point F2 dans la sphère. F2 se situe sur l'axe optique entre la surface et le centre de la sphère. La distance entre F2 et la surface est de l'indice F2. Sur les deux figures, l'indice de réfraction de l'air est n1 et celui de la sphère est supérieur de n2 à n1.
    Figure\(\PageIndex{4}\) : (a) Premier foyer (appelé « foyer de l'objet ») pour la réfraction sur une surface convexe. (b) Deuxième foyer (appelé « foyer de l'image ») pour la réfraction sur une surface convexe.

    Nous pouvons trouver l'emplacement\(f_1\) de la première mise au point\(F_1\)\(d_i=\infty\) en utilisant l'équation \ ref {eq20}.

    \[ \begin{align} \dfrac{n_1}{f_1}+\dfrac{n_2}{\infty} &=\dfrac{n_2−n_1}{R} \\[4pt] f_1 &=\dfrac{n_1R}{n_2−n_1} \end{align} \nonumber \]

    De même, nous pouvons définir un second foyer ou un foyer d'image\(F_2\) où l'image est formée pour un objet éloigné (Figure\(\PageIndex{4b}\)). L'emplacement du second foyer\(F_2\) est obtenu à partir de l'équation \ ref {eq20} en réglant\(d_0=\infty\) :

    \[ \begin{align} \dfrac{n_1}{\infty}+\dfrac{n_2}{f_2}=\dfrac{n_2−n_1}{R} \\[4pt] f_2=\dfrac{n_2R}{n_2−n_1}. \end{align} \nonumber \]

    Notez que le focus de l'objet se trouve à une distance du sommet différente de celle du focus de l'image pour les raisons suivantes\(n_1≠n_2\) :

    Convention de signalisation pour les surfaces à réfraction unique

    Bien que nous ayons dérivé cette équation pour la réfraction sur une surface convexe, la même expression vaut pour une surface concave, à condition d'utiliser la convention des signes suivante :

    1. \(R>0\)si la surface est convexe vers l'objet ; dans le cas contraire,\(R<0\).
    2. \(d_i>0\)si l'image est réelle et située à l'opposé de l'objet ; dans le cas contraire,\(d_i<0\).