2.3 : Miroirs sphériques

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Décrire la formation d'images par des miroirs sphériques
• Utilisez des diagrammes de rayons et l'équation du miroir pour calculer les propriétés d'une image dans un miroir sphérique.

L'image dans un miroir plan a la même taille que l'objet, est verticale et se trouve à la même distance derrière le miroir que l'objet se trouve devant le miroir. Un miroir incurvé, quant à lui, peut former des images qui peuvent être plus grandes ou plus petites que l'objet et peuvent se former devant ou derrière le miroir. En général, toute surface incurvée forme une image, bien que certaines images soient tellement déformées qu'elles deviennent méconnaissables (pensez à des miroirs de maison amusants). Comme les miroirs incurvés peuvent créer une telle variété d'images, ils sont utilisés dans de nombreux dispositifs optiques qui trouvent de nombreuses utilisations. Nous nous concentrerons principalement sur les miroirs sphériques, car ils sont plus faciles à fabriquer que les miroirs tels que les miroirs paraboliques et sont donc plus courants.

Miroirs courbes

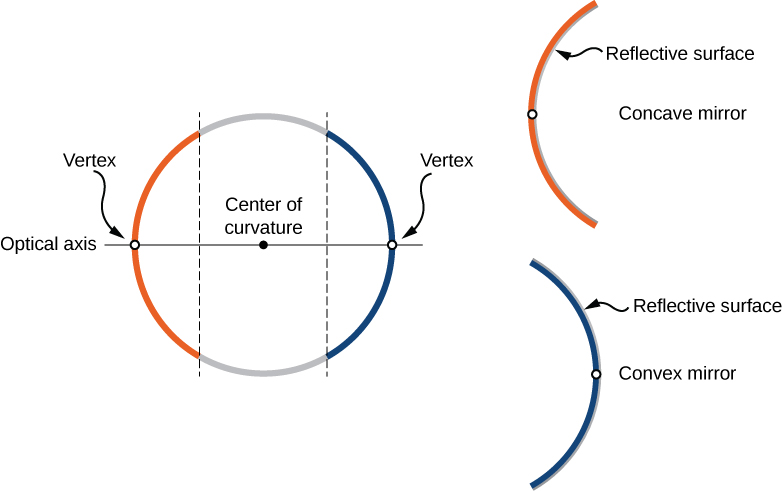
Nous pouvons définir deux types généraux de miroirs sphériques. Si la surface réfléchissante est la face extérieure de la sphère, le miroir est appelé miroir convexe. Si la surface intérieure est la surface réfléchissante, on parle de miroir concave.

La symétrie est l'une des principales caractéristiques de nombreux dispositifs optiques, y compris les miroirs et les lentilles. L'axe de symétrie de tels éléments optiques est souvent appelé axe principal ou axe optique. Pour un miroir sphérique, l'axe optique passe par le centre de courbure du miroir et le sommet du miroir, comme indiqué sur la figure\(\PageIndex{1}\).

Chiffre\(\PageIndex{1}\). Un miroir sphérique est formé en découpant un morceau de sphère et en argentant la surface intérieure ou extérieure. La surface intérieure d'un miroir concave est argentée (pensez à une « grotte ») et celle d'un miroir convexe est argentée sur la surface extérieure.

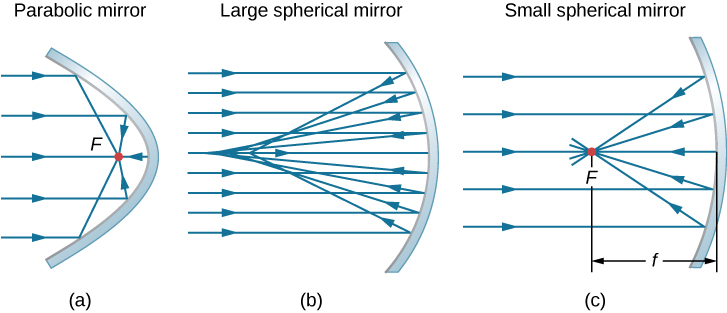
Considérez les rayons parallèles à l'axe optique d'un miroir parabolique, comme le montre la figure\(\PageIndex{2a}\). Selon la loi de réflexion, ces rayons sont réfléchis de telle sorte qu'ils convergent vers un point, appelé point focal. La figure\(\PageIndex{2b}\) montre un miroir sphérique de grande taille par rapport à son rayon de courbure. Pour ce miroir, les rayons réfléchis ne se croisent pas au même point, de sorte que le miroir n'a pas de point focal bien défini. C'est ce que l'on appelle l'aberration sphérique et produit une image floue d'un objet étendu. La figure\(\PageIndex{2c}\) montre un miroir sphérique petit par rapport à son rayon de courbure. Ce miroir est une bonne approximation d'un miroir parabolique, de sorte que les rayons qui arrivent parallèlement à l'axe optique sont réfléchis vers un point focal bien défini. La distance le long de l'axe optique entre le miroir et le point focal est appelée distance focale du miroir.

Figure\(\PageIndex{2}\) : (a) Les rayons parallèles réfléchis par un miroir parabolique se croisent en un point unique appelé point focal F. (b) Les rayons parallèles réfléchis par un grand miroir sphérique ne se croisent pas en un point commun. (c) Si un miroir sphérique est petit par rapport à son rayon de courbure, il se rapproche mieux de la partie centrale d'un miroir parabolique, de sorte que les rayons parallèles se croisent essentiellement en un point commun. La distance le long de l'axe optique entre le miroir et le point focal est la distance focale f du miroir.

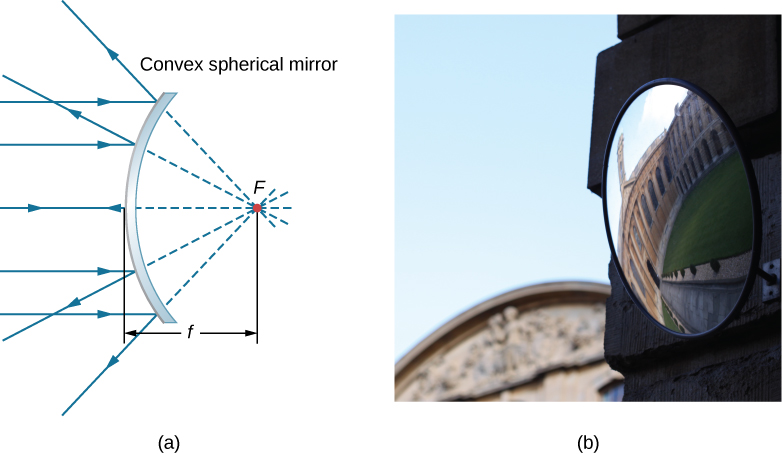
Un miroir sphérique convexe possède également un point focal, comme le montre la figure\(\PageIndex{3}\). Les rayons incidents parallèles à l'axe optique sont réfléchis par le miroir et semblent provenir d'un point situé\(F\) à distance focale\(f\) situé derrière le miroir. Ainsi, le point focal est virtuel car aucun rayon réel ne le traverse réellement ; ils semblent seulement provenir de lui.

Figure\(\PageIndex{3}\) : (a) Rayons réfléchis par un miroir sphérique convexe : Les rayons lumineux incidents parallèles à l'axe optique sont réfléchis par un miroir sphérique convexe et semblent provenir d'un point focal bien défini situé à la distance focale f sur le côté opposé du miroir. Le point focal est virtuel car aucun rayon réel ne le traverse. (b) Photographie d'une image virtuelle formée par un miroir convexe. (crédit b : modification d'une œuvre de Jenny Downing)

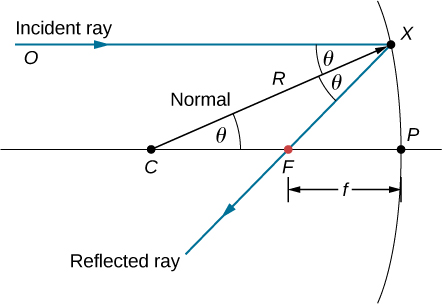
Quel est le rapport entre la distance focale d'un miroir et son rayon de courbure ? La figure\(\PageIndex{4}\) montre un seul rayon réfléchi par un miroir concave sphérique. Le rayon incident est parallèle à l'axe optique. Le point où le rayon réfléchi traverse l'axe optique est le point focal. Notez que tous les rayons incidents parallèles à l'axe optique sont réfléchis par le point focal. Par souci de simplicité, nous n'affichons qu'un seul rayon. Nous voulons savoir comment la distance focale\(FP\) (désignée par\(f\)) est liée au rayon de courbure du miroir\(R\), dont la longueur est

\[R=CF+FP. \label{eq31} \]

La loi de réflexion nous indique que les angles\(\angle OXC\) et\(\angle CXF\) sont les mêmes, et comme le rayon incident est parallèle à l'axe optique, les angles\(\angle OXC\) et\(\angle XCP\) les sont également les mêmes. Ainsi, le triangle\(CXF\) est un triangle isocèle avec\(CF=FX\). Si l'angle\(θ\) est petit alors

\[\sin θ≈ θ \label{sma} \]

qui est appelée « approximation aux petits angles »), alors\(FX≈FP\) ou\(CF≈FP\). En insérant ceci dans l'équation \ ref {eq31} pour le rayon\(R\), nous obtenons

\[\begin{align} R &=CF+FP \nonumber \\[4pt] &=FP+FP \nonumber \\[4pt] &=2FP\nonumber \\[4pt] &=2f \end{align} \nonumber \]

En d'autres termes, dans l'approximation du petit angle, la distance focale\(f\) d'un miroir sphérique concave est la moitié de son rayon de courbure,\(R\) :

\[f=\dfrac{R}{2}. \nonumber \]

Dans ce chapitre, nous supposons que l'approximation aux petits angles (également appelée approximation paraxiale) est toujours valide. Dans cette approximation, tous les rayons sont des rayons paraxiaux, ce qui signifie qu'ils forment un petit angle avec l'axe optique et se trouvent à une distance bien inférieure au rayon de courbure de l'axe optique. Dans ce cas, leurs angles\(θ\) de réflexion sont de petits angles, donc

\[\sin θ≈ \tan θ≈ θ. \label{smallangle} \]

Figure\(\PageIndex{4}\) : Réflexion dans un miroir concave. Dans l'approximation du petit angle, un rayon parallèle à l'axe optique CP est réfléchi à travers le point focal F du miroir.

Utilisation du ray tracing pour localiser des images

Pour trouver l'emplacement d'une image formée par un miroir sphérique, nous utilisons d'abord le ray tracing, qui est la technique qui consiste à dessiner des rayons et à utiliser la loi de réflexion pour déterminer les rayons réfléchis (plus tard, pour les lentilles, nous utilisons la loi de réfraction pour déterminer les rayons réfractés). Combiné à certaines géométries de base, nous pouvons utiliser le ray tracing pour trouver le point focal, l'emplacement de l'image et d'autres informations sur la façon dont un miroir manipule la lumière. En fait, nous avons déjà utilisé le ray tracing ci-dessus pour localiser le point focal des miroirs sphériques, ou la distance d'image des miroirs plats. Pour localiser l'image d'un objet, vous devez localiser au moins deux points de l'image. Pour localiser chaque point, il faut dessiner au moins deux rayons à partir d'un point de l'objet et construire leurs rayons réfléchis. Le point d'intersection des rayons réfléchis, que ce soit dans l'espace réel ou dans l'espace virtuel, est celui où se trouve le point correspondant de l'image. Pour faciliter le traçage des rayons, nous nous concentrons sur quatre rayons « principaux » dont les réflexions sont faciles à construire.

La figure\(\PageIndex{5}\) montre un miroir concave et un miroir convexe, chacun avec un objet en forme de flèche devant lui. Il s'agit des objets dont nous voulons localiser les images par ray tracing. Pour ce faire, nous dessinons des rayons à partir\(Q\) d'un point situé sur l'objet mais pas sur l'axe optique. Nous choisissons de dessiner notre rayon depuis la pointe de l'objet. Le rayon principal 1 part du point\(Q\) et se déplace parallèlement à l'axe optique. La réflexion de ce rayon doit passer par le point focal, comme indiqué ci-dessus. Ainsi, pour le miroir concave, la réflexion du rayon principal 1 passe par le point focal\(F\), comme le montre la figure\(\PageIndex{5b}\). Pour le miroir convexe, l'extension vers l'arrière de la réflexion du rayon principal 1 passe par le point focal (c'est-à-dire un foyer virtuel). Le rayon principal 2 se déplace d'abord sur la ligne passant par le point focal, puis est réfléchi le long d'une ligne parallèle à l'axe optique. Le rayon principal 3 se déplace vers le centre de courbure du miroir, de sorte qu'il frappe le miroir à incidence normale et est réfléchi le long de la ligne d'où il provient. Enfin, le rayon principal 4 atteint le sommet du miroir et est réfléchi symétriquement par rapport à l'axe optique.

Figure\(\PageIndex{5}\) : Les quatre rayons principaux représentés à la fois pour (a) un miroir concave et (b) un miroir convexe. L'image se forme à l'intersection des rayons (pour les images réelles) ou à l'endroit où leurs extensions vers l'arrière se croisent (pour les images virtuelles).

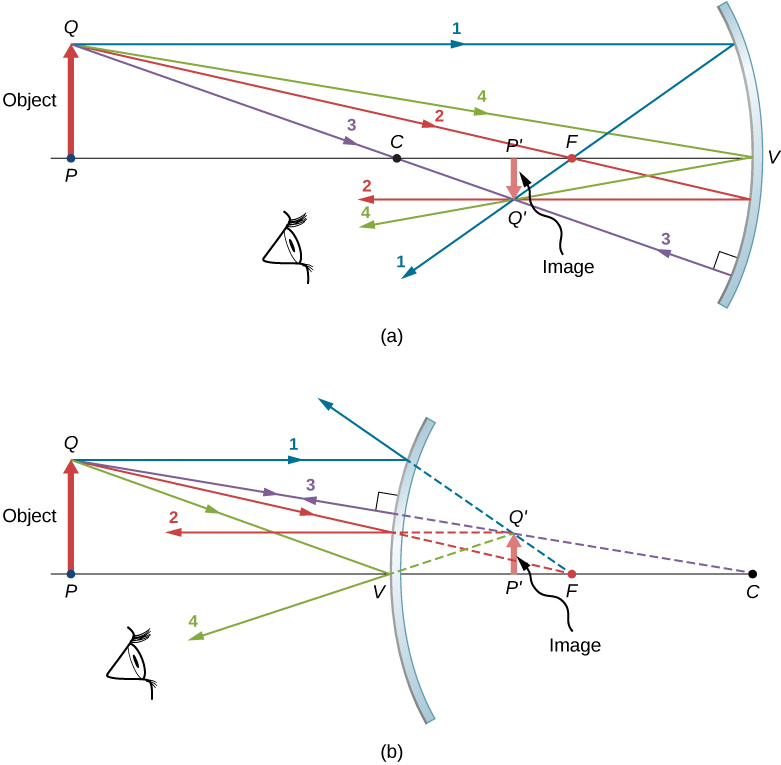
Les quatre rayons principaux se croisent au point\(Q′\), où se\(Q\) trouve l'image du point. Pour localiser un point\(Q′\), il suffirait de dessiner deux de ces rayons principaux. Nous sommes donc libres de choisir le rayonnement principal que nous souhaitons pour localiser l'image. Il est parfois utile de dessiner plus de deux rayons principaux pour vérifier que le tracé des rayons est correct.

Pour localiser complètement l'image étendue, nous devons localiser un deuxième point dans l'image, afin de savoir comment l'image est orientée. Pour ce faire, on trace les principaux rayons depuis la base de l'objet. Dans ce cas, les quatre rayons principaux circulent le long de l'axe optique, sont réfléchis par le miroir, puis repartent le long de l'axe optique. La difficulté est que, comme ces rayons sont colinéaires, nous ne pouvons pas déterminer un point unique où ils se croisent. Tout ce que nous savons, c'est que la base de l'image se trouve sur l'axe optique. Toutefois, comme le miroir est symétrique de haut en bas, il ne modifie pas l'orientation verticale de l'objet. Ainsi, comme l'objet est vertical, l'image doit être verticale. Par conséquent, l'image de la base de l'objet se trouve sur l'axe optique directement au-dessus de l'image de la pointe, comme indiqué sur la figure.

Pour le miroir concave, l'image étendue se forme dans ce cas entre le point focal et le centre de courbure du miroir. Elle est inversée par rapport à l'objet, est une image réelle et est plus petite que l'objet. Si nous rapprochions ou éloignions l'objet du miroir, les caractéristiques de l'image changeraient. Par exemple, nous montrons, dans un exercice ultérieur, qu'un objet placé entre un miroir concave et son point focal conduit à une image virtuelle verticale et plus grande que l'objet. Pour le miroir convexe, l'image étendue se forme entre le point focal et le miroir. Elle est verticale par rapport à l'objet, est une image virtuelle et est plus petite que l'objet.

Règles du Ray-Tracing

Le ray tracing est très utile pour les miroirs. Les règles du ray tracing sont résumées ici à titre de référence :

• Un rayon se déplaçant parallèlement à l'axe optique d'un miroir sphérique est réfléchi le long d'une ligne passant par le point focal du miroir (rayon 1 sur la figure\(\PageIndex{5}\)).
• Un rayon se déplaçant le long d'une ligne passant par le point focal d'un miroir sphérique est réfléchi le long d'une ligne parallèle à l'axe optique du miroir (rayon 2 sur la figure\(\PageIndex{5}\)).
• Un rayon se déplaçant le long d'une ligne passant par le centre de courbure d'un miroir sphérique est réfléchi le long de la même ligne (rayon 3 sur la figure\(\PageIndex{5}\)).
• Un rayon qui frappe le sommet d'un miroir sphérique est réfléchi symétriquement par rapport à l'axe optique du miroir (rayon 4 sur la figure\(\PageIndex{5}\)).

Nous utilisons le ray tracing pour illustrer la façon dont les images sont formées par les miroirs et pour obtenir des informations numériques sur les propriétés optiques du miroir. Si nous supposons qu'un miroir est petit par rapport à son rayon de courbure, nous pouvons également utiliser l'algèbre et la géométrie pour dériver une équation miroir, ce que nous ferons dans la section suivante. La combinaison du ray tracing avec l'équation du miroir est un bon moyen d'analyser les systèmes de miroirs.

Formation d'images par réflexion : équation miroir

Pour un miroir plan, nous avons montré que l'image formée a la même hauteur et la même orientation que l'objet, et qu'elle est située à la même distance derrière le miroir que l'objet se trouve devant le miroir. Bien que la situation soit un peu plus compliquée pour les miroirs incurvés, l'utilisation de la géométrie conduit à des formules simples reliant les distances entre l'objet et l'image aux distances focales des miroirs concaves et convexes.

Figure\(\PageIndex{6}\) : Image formée par un miroir concave.

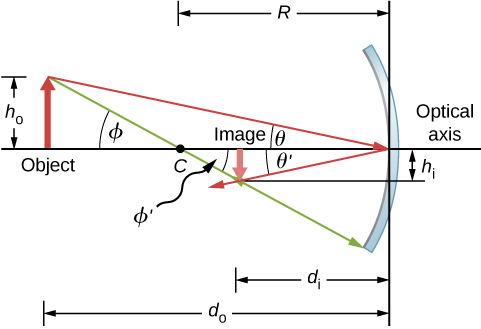
Considérez l'objet\(OP\) illustré sur la figure\(\PageIndex{6}\). Le centre de courbure du miroir est étiqueté\(C\) et correspond à une\(R\) distance du sommet du miroir, comme indiqué sur la figure. Les distances entre l'objet et l'image sont étiquetées\(d_o\) et\(d_i\), et les hauteurs de l'objet et de l'image sont étiquetées\(h_o\) et\(h_i\), respectivement. Comme les angles\(ϕ\) et\(ϕ′\) sont des angles intérieurs alternés, nous savons qu'ils ont la même amplitude. Cependant, leur signe doit être différent si nous mesurons des angles par rapport à l'axe optique, donc\(ϕ=−ϕ′\). Un scénario analogue vaut pour les angles\(θ\) et\(θ′\). La loi de réflexion nous indique qu'ils ont la même magnitude, mais que leurs signes doivent être différents si l'on mesure des angles par rapport à l'axe optique. Ainsi,\(θ=−θ′\). Prendre la tangente des angles\(θ\) et\(θ′\) utiliser la propriété qui\(\tan(−θ)=−\tan θ\) nous donne

\[\left. \begin{array}{rcl} \tanθ=\dfrac{h_o}{d_o} \\ \tanθ′=−\tanθ=\dfrac{h_i}{d_i} \end{array}\right\} =\dfrac{h_o}{d_o}=−\dfrac{h_i}{d_i} \label{eq51} \]

ou

\[- \dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}.\label{eq52} \]

De même, prendre la tangente de\(ϕ\) et\(ϕ′\) donne

\[\left. \begin{array}{rcl} \tanϕ=\dfrac{h_o}{d_o-R} \\ \tanϕ′=−\tanϕ=\dfrac{h_i}{R-d_i} \end{array}\right\} =\dfrac{h_o}{d_o-R}=−\dfrac{h_i}{R-d_i} \nonumber \]

ou

\[−\dfrac{h_o}{h_i}=\dfrac{d_o-R}{R-d_i}. \label{eq55} \]

La combinaison des équations \ ref {eq51} et \ ref {eq55} donne

\[\dfrac{d_o}{d_i}=\dfrac{d_o−R}{R−d_i}. \nonumber \]

Après un peu d'algèbre, cela devient

\[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{2}{R}. \label{eq57} \]

Aucune approximation n'est requise pour ce résultat, il est donc exact. Cependant, comme indiqué ci-dessus, dans l'approximation du petit angle, la distance focale d'un miroir sphérique est égale à la moitié du rayon de courbure du miroir, ou\(f=R/2\). En insérant ceci dans l'équation \ ref {eq57}, vous obtenez l'équation miroir :

\[\underbrace{ \dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f}}_{\text{mirror equation}}. \label{mirror equation} \]

L'équation du miroir met en relation les distances entre l'image et l'objet et la distance focale et n'est valable que dans l'approximation aux petits angles (Équation \ ref {sma}). Bien qu'il ait été dérivé pour un miroir concave, il vaut également pour les miroirs convexes (preuve que cela n'est qu'un exercice). Nous pouvons étendre l'équation du miroir au cas d'un miroir plan en notant qu'un miroir plan a un rayon de courbure infini. Cela signifie que le point focal est à l'infini, de sorte que l'équation du miroir se simplifie

\[d_o=−d_i \nonumber \]

qui est la même équation que celle obtenue précédemment.

Notez que nous avons fait très attention aux signes lors de la dérivation de l'équation miroir. Pour un miroir plan, la distance de l'image a le signe opposé à la distance de l'objet. De plus, l'image réelle formée par le miroir concave de la figure\(\PageIndex{6}\) se trouve du côté opposé de l'axe optique par rapport à l'objet. Dans ce cas, la hauteur de l'image doit avoir le signe opposé à la hauteur de l'objet. Pour suivre les signes des différentes quantités dans l'équation miroir, nous introduisons maintenant une convention des signes.

Convention de signalisation pour rétroviseurs sphériques

L'utilisation d'une convention de signes cohérente est très importante en optique géométrique. Il attribue des valeurs positives ou négatives aux grandeurs qui caractérisent un système optique. Comprendre la convention des signes permet de décrire une image sans créer de diagramme à rayons. Ce texte utilise la convention de signalisation suivante :

1. La distance focale\(f\) est positive pour les miroirs concaves et négative pour les miroirs convexes.
2. La distance d'image\(d_i\) est positive pour les images réelles et négative pour les images virtuelles.

Notez que la règle 1 signifie que le rayon de courbure d'un miroir sphérique peut être positif ou négatif. Qu'est-ce que cela signifie d'avoir un rayon de courbure négatif ? Cela signifie simplement que le rayon de courbure d'un miroir convexe est défini comme étant négatif.

Agrandissement d'image

Utilisons la convention des signes pour mieux interpréter la dérivation de l'équation miroir. En dérivant cette équation, nous avons découvert que les hauteurs de l'objet et de l'image sont liées par

\[−\dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}. \label{eq61} \]

Voir l'équation \ ref {eq52}. L'objet et l'image formés par le miroir de la figure\(\PageIndex{6}\) sont réels, de sorte que les distances entre l'objet et l'image sont toutes deux positives. Le point le plus élevé de l'objet se trouve au-dessus de l'axe optique, de sorte que la hauteur de l'objet est positive. L'image se trouve toutefois en dessous de l'axe optique, de sorte que la hauteur de l'image est négative. Ainsi, cette convention des signes est cohérente avec notre dérivation de l'équation miroir.

L'équation \ ref {eq61} décrit en fait le grossissement linéaire (souvent simplement appelé « grossissement ») de l'image en termes de distance entre l'objet et l'image. Nous définissons ainsi le grossissement adimensionnel\(m\) comme suit :

\[\underbrace{m=\dfrac{h_i}{h_o}}_{\text{linear magnification}}. \label{mag} \]

Si elle\(m\) est positive, l'image est verticale et si elle\(m\) est négative, l'image est inversée. Si\(|m|>1\), l'image est plus grande que l'objet, et si\(|m|<1\), l'image est plus petite que l'objet. Avec cette définition du grossissement, nous obtenons la relation suivante entre les distances verticale et horizontale entre l'objet et l'image :

\[m=\dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o}. \nonumber \]

Cette relation est très utile car elle vous permet d'obtenir le grossissement de l'image à partir de l'objet et les distances de l'image, que vous pouvez obtenir à partir de l'équation miroir.

Exemple\(\PageIndex{1}\): Solar Electric Generating System

L'une des technologies solaires utilisées aujourd'hui pour produire de l'électricité implique un dispositif (appelé cuvette parabolique ou capteur de concentration) qui concentre la lumière solaire sur un tuyau noirci contenant un fluide. Ce fluide chauffé est pompé vers un échangeur de chaleur, où l'énergie thermique est transférée vers un autre système qui est utilisé pour générer de la vapeur et finalement de l'électricité par le biais d'un cycle de vapeur conventionnel. La figure\(\PageIndex{7}\) montre un tel système de fonctionnement dans le sud de la Californie. Le vrai miroir est un cylindre parabolique dont le point focal est situé sur le tube ; cependant, nous pouvons approximer le miroir comme étant exactement le quart d'un cylindre circulaire.

Figure\(\PageIndex{7}\) : Des collecteurs paraboliques sont utilisés pour produire de l'électricité dans le sud de la Californie. (crédit : « kjkolb » /Wikimedia Commons)

1. Si nous voulons que les rayons du soleil se focalisent à 40,0 cm du miroir, quel est le rayon du miroir ?
2. Quelle est la quantité de lumière solaire concentrée sur le tuyau, par mètre de longueur de tuyau, en supposant que l'insolation (rayonnement solaire incident) est de 900 W/m ² ?
3. Si le tuyau transportant le fluide a un diamètre de 2 cm, quelle est l'augmentation de la température du fluide par mètre de tuyau sur une période d'une minute ? Supposons que tout le rayonnement solaire incident sur le réflecteur soit absorbé par le tuyau et que le fluide soit de l'huile minérale.

Stratégie

Déterminez d'abord les principes physiques impliqués. La partie (a) concerne l'optique des miroirs sphériques. La partie (b) implique un peu de mathématiques, principalement de géométrie. La partie (c) nécessite une compréhension de la chaleur et de la densité.

Solution

a. Le soleil est l'objet, donc la distance de l'objet est essentiellement infinie :\(d_o=\infty\). La distance d'image souhaitée est de\(d_i=40.0\,cm\). Nous utilisons l'équation du miroir (équation \ ref {équation miroir}) pour déterminer la distance focale du miroir :

\[\begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &=\dfrac{1}{f} \nonumber \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{\infty}+\dfrac{1}{40.0\,cm}\right)^{−1} \\[4pt] &= 40.0 \,cm \end{align*} \nonumber \]

Ainsi, le rayon du miroir est

\[R=2f=80.0\,cm. \nonumber \]

b. L'ensoleillement est de 900 W/m ². Vous devez trouver la section transversale\(A\) du miroir concave, car la puissance délivrée est\(900\, W/m^2×A\). Dans ce cas, le miroir est un quart de section d'un cylindre, donc la surface sur une longueur\(L\) du miroir est\(A=\frac{1}{4}(2πR)L\). La surface sur une longueur de 1,00 m est alors

\[\begin{align*} A&=\dfrac{\pi}{2}R(1.00m) \\[4pt] &=\dfrac{(3.14)}{2}(0.800\,m)(1.00\,m) \\[4pt] &=1.26\,m^2. \end{align*} \nonumber \]

L'insolation sur la longueur de 1,00 m de tuyau est alors

\[(9.00×10^2\dfrac{W}{m^2})(1.26\,m^2)=1130\,W. \nonumber \]

c. L'augmentation de température est donnée par\(Q=mcΔT\). La masse\(m\) d'huile minérale dans la section d'un mètre de tuyau est

\[ \begin{align*} m &= ρV = ρπ\left(\dfrac{d}{2}\right)^2(1.00\,m) \nonumber \\[4pt] &=(8.00×10^2kg/m^3)(3.14)(0.0100\,m)^2(1.00\,m) \nonumber \\[4pt] &=0.251\,kg \end{align*} \nonumber \]

Par conséquent, l'augmentation de la température en une minute est

\[ \begin{align*} \Delta T&= \dfrac{Q}{mc} \nonumber \\[4pt] &=\dfrac{(1130\,W)(60.0\,s)}{(0.251\,kg)(1670\,J⋅kg/°C)} \nonumber \\[4pt] &=162°\end{align*} \nonumber \]

L'importance

Un ensemble de tuyaux de ce type dans le désert californien peut fournir une puissance thermique de 250 MW par temps ensoleillé, les fluides pouvant atteindre des températures allant jusqu'à 400 °C. Nous ne prenons ici qu'un mètre de tuyau et ignorons les pertes de chaleur le long du tuyau.

Exemple\(\PageIndex{2}\): Image in a Convex Mirror

Un kératomètre est un appareil utilisé pour mesurer la courbure de la cornée de l'œil, notamment pour la pose de lentilles de contact. La lumière est réfléchie par la cornée, qui agit comme un miroir convexe, et le kératomètre mesure le grossissement de l'image. Plus le grossissement est faible, plus le rayon de courbure de la cornée est petit. Si la source lumineuse se trouve à 12 cm de la cornée et que le grossissement de l'image est de 0,032, quel est le rayon de courbure de la cornée ?

Stratégie

Si vous trouvez la distance focale du miroir convexe formé par la cornée, vous connaissez son rayon de courbure (c'est le double de la distance focale). La distance de l'objet est d _o = 12 cm et le grossissement est m = 0,032. Trouvez d'abord la distance de l'image,\(d_i\) puis déterminez la distance focale\(f\).

Solution

Commencez par l'équation de grossissement (Equation \ ref {mag}) et la résolution\(d_i\) et l'insertion des valeurs données donnent

\[d_i=−m d_o=−(0.032)(12\,cm)=−0.384\,cm \nonumber \]

où nous avons retenu un chiffre très significatif car il s'agit d'une étape intermédiaire du calcul. Résolvez l'équation miroir pour la distance focale\(f\) et insérez les valeurs connues pour les distances entre l'objet et l'image. Le résultat est

\[ \begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &= \dfrac{1}{f} \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1}  \\[4pt] &= \left(\dfrac{1}{12cm}+\dfrac{1}{-0.384cm}\right)^{−1} \\[4pt] &=-40.0 \,cm \end{align*} \nonumber \]

Le rayon de courbure est le double de la distance focale, donc

\[R=2f=−0.80\,cm \nonumber \]

L'importance

La distance focale étant négative, la mise au point est virtuelle, comme prévu pour un miroir concave et un objet réel. Le rayon de courbure trouvé ici est raisonnable pour une cornée. La distance entre la cornée et la rétine chez un adulte est d'environ 2,0 cm. Dans la pratique, les cornées peuvent ne pas être sphériques, ce qui complique la pose des lentilles de contact. Notez que la distance de l'image ici est négative, ce qui correspond au fait que l'image se trouve derrière le miroir. Ainsi, l'image est virtuelle car aucun rayon ne la traverse réellement. Dans les problèmes et les exercices, vous allez montrer que, pour une distance d'objet fixe, un rayon de courbure plus petit correspond à un grossissement plus faible.

STRATÉGIE DE RÉSOLUTION DE PROBLÈMES : MIROIRS SPHÉRIQUES

• Étape 1. Assurez-vous d'abord que la formation de l'image par un miroir sphérique est impliquée.
• Étape 2. Déterminez si le traçage des rayons, l'équation du miroir ou les deux sont nécessaires. Un croquis est très utile même si le problème ne nécessite pas spécifiquement le ray tracing. Écrivez des symboles et des valeurs connues sur l'esquisse.
• Étape 3. Identifiez exactement ce qui doit être déterminé dans le problème (identifiez les inconnues).
• Étape 4. Dressez une liste de ce qui est indiqué ou peut être déduit du problème tel qu'indiqué (identifier les éléments connus).
• Étape 5. Si le ray tracing est requis, utilisez les règles de ray tracing répertoriées au début de cette section.
• Étape 6. La plupart des problèmes quantitatifs nécessitent l'utilisation de l'équation miroir. Utilisez les exemples comme guides pour utiliser l'équation miroir.
• Étape 7. Vérifiez si la réponse est logique. Les signes de distance de l'objet, de distance de l'image et de distance focale correspondent-ils à ce que l'on attend du ray tracing ? Le signe du grossissement est-il correct ? Les distances entre l'objet et l'image sont-elles raisonnables ?

Écart par rapport à l'approximation aux petits angles

L'approximation du petit angle (équation \ ref {smallangle}) est la pierre angulaire de la discussion ci-dessus sur la formation d'images par un miroir sphérique. Lorsque cette approximation n'est pas respectée, l'image créée par un miroir sphérique se déforme. Une telle distorsion est appelée aberration. Nous discutons ici brièvement de deux types spécifiques d'aberrations : l'aberration sphérique et la coma.

Aberration sphérique

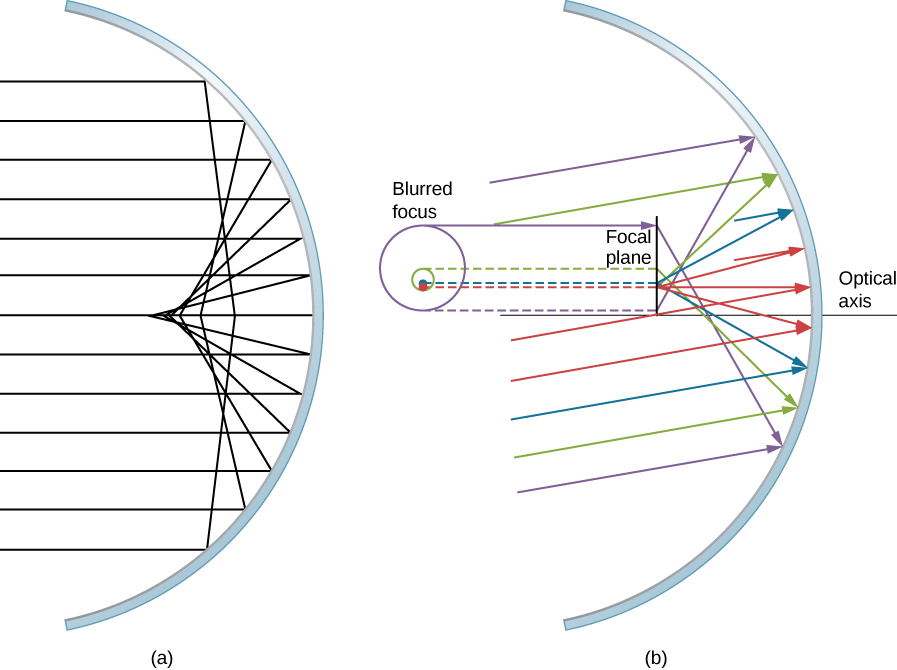
Prenons l'exemple d'un large faisceau de rayons parallèles heurtant un miroir sphérique, comme le montre la figure\(\PageIndex{8}\). Plus les rayons s'éloignent de l'axe optique, plus le miroir sphérique se rapproche d'un miroir parabolique. Ainsi, ces rayons ne sont pas focalisés au même point que les rayons proches de l'axe optique, comme le montre la figure. En raison de l'aberration sphérique, l'image d'un objet étendu dans un miroir sphérique sera floue. Les aberrations sphériques sont caractéristiques des miroirs et des lentilles que nous examinons dans la section suivante de ce chapitre (des miroirs et des lentilles plus sophistiqués sont nécessaires pour éliminer les aberrations sphériques).

Figure\(\PageIndex{8}\) : (a) Dans le cas d'une aberration sphérique, les rayons les plus éloignés de l'axe optique et les rayons les plus proches de l'axe optique sont focalisés en différents points. Notez que l'aberration s'aggrave pour les rayons plus éloignés de l'axe optique. (b) Pour l'aberration comatique, les rayons parallèles qui ne sont pas parallèles à l'axe optique sont focalisés à différentes hauteurs et à différentes distances focales, de sorte que l'image contient une « queue » comme une comète (qui est « coma » en latin). Notez que les rayons colorés servent uniquement à faciliter la visualisation ; les couleurs n'indiquent pas la couleur de la lumière.

Coma ou aberration comatique

Le coma est similaire à l'aberration sphérique, mais se produit lorsque les rayons entrants ne sont pas parallèles à l'axe optique, comme le montre la figure\(\PageIndex{8b}\). Rappelez-vous que l'approximation du petit angle vaut pour les miroirs sphériques qui sont petits par rapport à leur rayon. Dans ce cas, les miroirs sphériques sont de bonnes approximations des miroirs paraboliques. Les miroirs paraboliques focalisent tous les rayons parallèles à l'axe optique au niveau du point focal. Cependant, les rayons parallèles qui ne sont pas parallèles à l'axe optique sont focalisés à différentes hauteurs et à différentes distances focales, comme le montre la figure\(\PageIndex{8b}\). Comme un miroir sphérique est symétrique par rapport à l'axe optique, les différents rayons colorés de cette figure créent des cercles de la couleur correspondante sur le plan focal.

Bien qu'un miroir sphérique soit représenté sur la figure\(\PageIndex{8b}\), une aberration comatique se produit également pour les miroirs paraboliques ; elle ne résulte pas d'une rupture de l'approximation du petit angle (équation \ ref {smallangle}). L'aberration sphérique, cependant, ne se produit que pour les miroirs sphériques et résulte d'une rupture de l'approximation du petit angle. Nous aborderons à la fois le coma et l'aberration sphérique plus loin dans ce chapitre, en relation avec les télescopes.