Skip to main content
Global

7.1E : Exercices pour la section 7.1

  1. Last updated
  2. Save as PDF
  • Page ID
    197638

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lorsque vous utilisez la technique de l'intégration par parties, vous devez choisir avec soin de quelle expression il s'agit\(u\). Pour chacun des problèmes suivants, utilisez les instructions de cette section pour faire votre choix\(u\). N'évaluez pas les intégrales.

    1)\(\displaystyle ∫x^3e^{2x}\,dx\)

    Réponse
    \( u=x^3\)

    2)\(\displaystyle ∫x^3\ln(x)\,dx\)

    3)\(\displaystyle ∫y^3\cos y\,dy\)

    Réponse
    \(u=y^3\)

    4)\(\displaystyle ∫x^2\arctan x\,dx\)

    5)\(\displaystyle ∫e^{3x}\sin(2x)\,dx\)

    Réponse
    \(u=\sin(2x)\)

    Dans les exercices 6 à 37, trouvez l'intégrale en utilisant la méthode la plus simple. Tous les problèmes ne nécessitent pas une intégration par pièces.

    6)\(\displaystyle ∫v\sin v\,dv\)

    7)\(\displaystyle ∫\ln x\,dx\) (Astuce :\(\displaystyle ∫\ln x\,dx\) équivaut à\(\displaystyle ∫1⋅\ln(x)\,dx.)\)

    Réponse
    \(\displaystyle ∫\ln x\,dx \quad = \quad−x+x\ln x+C\)

    8)\(\displaystyle ∫x\cos x\,dx\)

    9)\(\displaystyle ∫\tan^{−1}x\,dx\)

    Réponse
    \(\displaystyle ∫\tan^{−1}x\,dx\quad = \quad x\tan^{−1}x−\tfrac{1}{2}\ln(1+x^2)+C\)

    10)\(\displaystyle ∫x^2e^x\,dx\)

    11)\(\displaystyle ∫x\sin(2x)\,dx\)

    Réponse
    \(\displaystyle ∫x\sin(2x)\,dx \quad = \quad −\tfrac{1}{2}x\cos(2x)+\tfrac{1}{4}\sin(2x)+C\)

    (12)\(\displaystyle ∫xe^{4x}\,dx\)

    13)\(\displaystyle ∫xe^{−x}\,dx\)

    Réponse
    \(\displaystyle ∫xe^{−x}\,dx \quad = \quad e^{−x}(−1−x)+C\)

    (14)\(\displaystyle ∫x\cos 3x\,dx\)

    15)\(\displaystyle ∫x^2\cos x\,dx\)

    Réponse
    \(\displaystyle ∫x^2\cos x\,dx \quad = \quad 2x\cos x+(−2+x^2)\sin x+C\)

    16)\(\displaystyle ∫x\ln x\,dx\)

    17)\(\displaystyle ∫\ln(2x+1)\,dx\)

    Réponse
    \(\displaystyle ∫\ln(2x+1)\,dx \quad = \quad \tfrac{1}{2}(1+2x)(−1+\ln(1+2x))+C\)

    18)\(\displaystyle ∫x^2e^{4x}\,dx\)

    19)\(\displaystyle ∫e^x\sin x\,dx\)

    Réponse
    \(\displaystyle ∫e^x\sin x\,dx \quad = \quad \tfrac{1}{2}e^x(−\cos x+\sin x)+C\)

    (20)\(\displaystyle ∫e^x\cos x\,dx\)

    (21)\(\displaystyle ∫xe^{−x^2}\,dx\)

    Réponse
    \(\displaystyle ∫xe^{−x^2}\,dx \quad = \quad −\frac{e^{−x^2}}{2}+C\)

    (22)\(\displaystyle ∫x^2e^{−x}\,dx\)

    23)\(\displaystyle ∫\sin(\ln(2x))\,dx\)

    Réponse
    \(\displaystyle ∫\sin(\ln(2x))\,dx \quad = \quad −\tfrac{1}{2}x\cos[\ln(2x)]+\tfrac{1}{2}x\sin[\ln(2x)]+C\)

    (24)\(\displaystyle ∫\cos(\ln x)\,dx\)

    25)\(\displaystyle ∫(\ln x)^2\,dx\)

    Réponse
    \(\displaystyle ∫(\ln x)^2\,dx \quad = \quad 2x−2x\ln x+x(\ln x)^2+C\)

    (26)\(\displaystyle ∫\ln(x^2)\,dx\)

    (27)\(\displaystyle ∫x^2\ln x\,dx\)

    Réponse
    \(\displaystyle ∫x^2\ln x\,dx \quad = \quad −\frac{x^3}{9}+\tfrac{1}{3}x^3\ln x+C\)

    (28)\(\displaystyle ∫\sin^{−1}x\,dx\)

    (29)\(\displaystyle ∫\cos^{−1}(2x)\,dx\)

    Réponse
    \(\displaystyle ∫\cos^{−1}(2x)\,dx \quad = \quad −\tfrac{1}{2}\sqrt{1−4x^2}+x\cos^{−1}(2x)+C\)

    (30)\(\displaystyle ∫x\arctan x\,dx\)

    31)\(\displaystyle ∫x^2\sin x\,dx\)

    Réponse
    \(\displaystyle ∫x^2\sin x\,dx \quad = \quad −(−2+x^2)\cos x+2x\sin x+C\)

    32)\(\displaystyle ∫x^3\cos x\,dx\)

    33)\(\displaystyle ∫x^3\sin x\,dx\)

    Réponse
    \(\displaystyle ∫x^3\sin x\,dx \quad = \quad −x(−6+x^2)\cos x+3(−2+x^2)\sin x+C\)

    34)\(\displaystyle ∫x^3e^x\,dx\)

    35)\(\displaystyle ∫x\sec^{−1}x\,dx\)

    Réponse
    \(\displaystyle ∫x\sec^{−1}x\,dx \quad = \quad \tfrac{1}{2}x\left(−\sqrt{1−\frac{1}{x^2}}+x⋅\sec^{−1}x\right)+C\)

    36)\(\displaystyle ∫x\sec^2x\,dx\)

    (37)\(\displaystyle ∫x\cosh x\,dx\)

    Réponse
    \(\displaystyle ∫x\cosh x\,dx \quad = \quad −\cosh x+x\sinh x+C\)

    Dans les exercices 38 à 46, calculez les intégrales définies. Utilisez un utilitaire graphique pour confirmer vos réponses.

    38)\(\displaystyle ∫^1_{1/e}\ln x\,dx\)

    39)\(\displaystyle ∫^1_0xe^{−2x}\,dx\) (Exprimez la réponse sous une forme exacte.)

    Réponse
    \(\displaystyle ∫^1_0xe^{−2x}\,dx \quad = \quad \frac{1}{4}−\frac{3}{4e^2}\)

    40)\(\displaystyle ∫^1_0e^{\sqrt{x}}\,dx \quad (\text{let}\, u=\sqrt{x})\)

    41)\(\displaystyle ∫^e_1\ln(x^2)\,dx\)

    Réponse
    \(\displaystyle ∫^e_1\ln(x^2)\,dx \quad = \quad 2\)

    42)\(\displaystyle ∫^π_0x\cos x\,dx\)

    43)\(\displaystyle ∫^π_{−π}x\sin x\,dx\) (Exprimez la réponse sous une forme exacte.)

    Réponse
    \(\displaystyle ∫^π_{−π}x\sin x\,dx \quad = \quad 2\pi\)

    44)\(\displaystyle ∫^3_0\ln(x^2+1)\,dx\) (Exprimez la réponse sous une forme exacte.)

    45)\(\displaystyle ∫^{π/2}_0x^2\sin x\,dx\) (Exprimez la réponse sous une forme exacte.)

    Réponse
    \(\displaystyle ∫^{π/2}_0x^2\sin x\,dx \quad = \quad −2+π\)

    46)\(\displaystyle ∫^1_0x5^x\,dx\) (Exprimez la réponse à l'aide de cinq chiffres significatifs.)

    47) Évaluer\(\displaystyle ∫\cos x\ln(\sin x)\,dx\)

    Réponse
    \(\displaystyle ∫\cos x\ln(\sin x)\,dx \quad = \quad −\sin(x)+\ln[\sin(x)]\sin x+C\)

    Dans les exercices 48 à 50, dérivez les formules suivantes en utilisant la technique de l'intégration par parties. Supposons qu'il\(n\) s'agisse d'un entier positif. Ces formules sont appelées formules de réduction car l'exposant du\(x\) terme a été réduit d'un dans chaque cas. La seconde intégrale est plus simple que l'intégrale d'origine.

    48)\(\displaystyle ∫x^ne^x\,dx=x^ne^x−n∫x^{n−1}e^x\,dx\)

    49)\(\displaystyle ∫x^n\cos x\,dx=x^n\sin x−n∫x^{n−1}\sin x\,dx\)

    Réponse
    Les réponses varient

    50)\(\displaystyle ∫x^n\sin x\,dx=\) ______

    51) Intégrez\(\displaystyle ∫2x\sqrt{2x−3}\,dx\) en utilisant deux méthodes :

    a. Utilisation de pièces, location\(dv=\sqrt{2x−3}\,dx\)

    b. Substitution, location\(u=2x−3\)

    Réponse
    a.\(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)
    b.\(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)

    Dans les exercices 52 à 57, indiquez si vous souhaitez utiliser l'intégration par parties pour évaluer l'intégrale. Si c'est le cas, identifiez\(u\) et\(dv\). Si ce n'est pas le cas, décrivez la technique utilisée pour effectuer l'intégration sans réellement résoudre le problème.

    52)\(\displaystyle ∫x\ln x\,dx\)

    53)\(\displaystyle ∫\frac{\ln^2x}{x}\,dx\)

    Réponse
    N'utilisez pas l'intégration par pièces. Choisissez\(u\) d'être\(\ln x\), et l'intégrale est de la forme\(\displaystyle ∫u^2\,du.\)

    (54)\(\displaystyle ∫xe^x\,dx\)

    55)\(\displaystyle ∫xe^{x^2−3}\,dx\)

    Réponse
    N'utilisez pas l'intégration par pièces. Laissez\(u=x^2−3\), et l'intégrale peut être mise dans le formulaire\(∫e^u\,du\).

    56)\(\displaystyle ∫x^2\sin x\,dx\)

    (57)\(\displaystyle ∫x^2\sin(3x^3+2)\,dx\)

    Réponse
    N'utilisez pas l'intégration par pièces. Choisissez\(u\) d'être\(u=3x^3+2\) et l'intégrale peut être mise dans la forme\(\displaystyle ∫\sin(u)\,du.\)

    Dans les exercices 58 à 59, esquissez la région délimitée au-dessus par la courbe,\(x\) l'axe -et\(x=1\), et trouvez l'aire de la région. Fournissez la forme exacte ou arrondissez les réponses au nombre de places indiqué.

    58)\(y=2xe^{−x}\) (Réponse approximative à quatre décimales.)

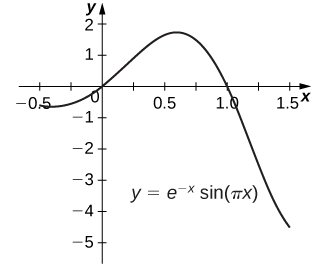
    59)\(y=e^{−x}\sin(πx)\) (Réponse approximative à cinq décimales.)

    Réponse
    La zone sous le graphique est\(0.39535 \, \text{units}^2.\)

    Dans les exercices 60 à 61, trouvez le volume généré en faisant pivoter la région délimitée par les courbes données autour de la ligne spécifiée. Exprimez les réponses sous une forme exacte ou approximative au nombre de décimales indiqué.

    60)\(y=\sin x,\,y=0,\,x=2π,\,x=3π;\) sur l'\(y\)axe -( Exprime la réponse sous forme exacte.)

    61)\(y=e^{−x}, \,y=0,\,x=−1, \, x=0;\) à propos de\(x=1\) (Exprimez la réponse sous forme exacte.)

    Réponse
    \(V = 2πe \, \text{units}^3\)

    62) Une particule se déplaçant le long d'une ligne droite a une vitesse d'\(v(t)=t^2e^{−t}\)après\(t\) seconde. Quelle distance parcoure-t-il dans les 2 premières secondes ? (Supposons que les unités soient exprimées en pieds et exprimez la réponse sous une forme exacte.)

    63) Trouvez l'aire sous le graphique\(y=\sec^3x\) de\(x=0\) à\(x=1\). (Arrondissez la réponse à deux chiffres significatifs.)

    Réponse
    \(A= 2.05 \, \text{units}^2\)

    64) Trouvez la zone comprise entre\(y=(x−2)e^x\) et l'\(x\)axe -de\(x=2\) à\(x=5\). (Exprimez la réponse sous une forme exacte.)

    65) Trouvez l'aire de la région délimitée par la courbe\(y=x\cos x\) et l'\(x\)axe -pour\(\frac{11π}{2}≤x≤\frac{13π}{2}.\) (Exprimez la réponse sous une forme exacte.)

    Réponse
    \(A = 12π \, \text{units}^2\)

    66) Déterminez le volume du solide généré en faisant tourner la région délimitée par la courbe\(y=\ln x\),\(x\) l'axe et la ligne verticale\(x=e^2\) autour de l'\(x\)axe. (Exprimez la réponse sous une forme exacte.)

    67) Déterminez le volume du solide généré en faisant tourner la région délimitée par la courbe\(y=4\cos x\) et l'\(x\)axe -,\(\frac{π}{2}≤x≤\frac{3π}{2},\) autour de l'\(x\)axe. (Exprimez la réponse sous une forme exacte.)

    Réponse
    \(V = 8π^2 \, \text{units}^3\)

    68) Déterminez le volume du solide généré en faisant tourner la région du premier quadrant délimité par\(y=e^x\) et par l'\(x\)axe -, de\(x=0\) à\(x=\ln(7)\), autour de l'\(y\)axe. (Exprimez la réponse sous une forme exacte.)

    69) Quel est le volume du gâteau Bundt résultant de la rotation\( y=\sin x\) autour de l'\(y\)axe -de\( x=0\) à\( x=π\) ?

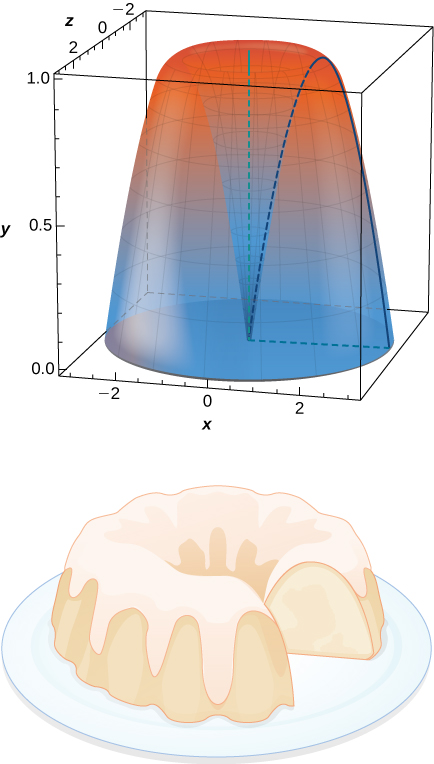
    Réponse
    \(V = 2π^2\)unités 3