29.2 : Un modèle de l'univers
- Page ID
- 192352
Objectifs d'apprentissage
À la fin de cette section, vous serez en mesure de :
- Expliquer comment le taux d'expansion de l'univers affecte son évolution
- Décrivez quatre possibilités pour l'évolution de l'univers
- Expliquez ce qui est en expansion lorsque nous disons que l'univers est en expansion
- Définissez la densité critique et les preuves que la matière seule dans l'univers est bien inférieure à la densité critique
- Décrivez ce que disent les observations sur l'avenir probable à long terme de l'univers
Utilisons maintenant les résultats concernant l'expansion de l'univers pour voir comment ces idées pourraient être appliquées pour développer un modèle pour l'évolution de l'univers dans son ensemble. Grâce à ce modèle, les astronomes peuvent faire des prédictions sur l'évolution de l'univers jusqu'à présent et sur ce qu'il adviendra de lui dans le futur.
L'univers en expansion
Chaque modèle de l'univers doit inclure l'expansion que nous observons. Un autre élément clé des modèles est que le principe cosmologique (dont nous avons discuté dans L'évolution et la distribution des galaxies) est valide : à grande échelle, l'univers est le même partout à tout moment (homogène et isotrope). Par conséquent, le taux d'expansion doit être le même partout à n'importe quelle époque du temps cosmique. Si c'est le cas, nous n'avons pas besoin de penser à l'univers tout entier lorsque nous pensons à l'expansion, nous pouvons simplement en regarder une partie suffisamment grande. (Certains modèles d'énergie noire permettraient au taux d'expansion d'être différent dans différentes directions, et les scientifiques conçoivent des expériences pour tester cette idée. Cependant, jusqu'à ce que de telles preuves soient trouvées, nous supposerons que le principe cosmologique s'applique à l'ensemble de l'univers.)
Dans Galaxies, nous avons laissé entendre que lorsque nous pensons à l'expansion de l'univers, il est plus correct de penser à l'espace lui-même qui s'étire plutôt qu'à des galaxies se déplaçant dans l'espace statique. Néanmoins, nous avons depuis discuté des décalages vers le rouge des galaxies comme s'ils résultaient du mouvement des galaxies elles-mêmes.
Cependant, il est temps maintenant de mettre fin à ces notions simplistes et de porter un regard plus sophistiqué sur l'expansion cosmique. Souvenez-vous de notre discussion sur la théorie de la relativité générale d'Einstein (dans le chapitre sur les trous noirs et l'espace-temps incurvé) que l'espace, ou plus précisément l'espace-temps, n'est pas une simple toile de fond pour l'action de l'univers, comme le pensait Newton. Il s'agit plutôt d'un participant actif, affecté par la matière et l'énergie de l'univers et affectant à son tour.
Puisque l'expansion de l'univers est l'étirement de tout l'espace-temps, tous les points de l'univers s'étendent ensemble. Ainsi, l'expansion a commencé partout à la fois. Malheureusement pour les agences de tourisme du futur, il n'y a aucun endroit où l'on puisse visiter où l'étirement de l'espace a commencé ou où l'on peut dire que le Big Bang s'est produit.
Pour décrire la façon dont l'espace s'étend, nous disons que l'expansion cosmique provoque un changement d'échelle uniforme de l'univers au fil du temps. Par échelle, nous entendons, par exemple, la distance entre deux amas de galaxies. Il est habituel de représenter l'échelle par le facteur\(R\) ; si elle est\(R\) double, cela signifie que la distance entre les clusters a doublé. Puisque l'univers se développe au même rythme partout, la variation de R nous indique dans quelle mesure il s'est développé (ou s'est contracté) à un moment donné. Pour un univers statique, R serait constant au fil du temps. Dans un univers en expansion, R augmente avec le temps.
Si c'est l'espace qui s'étire plutôt que les galaxies qui se déplacent dans l'espace, alors pourquoi les galaxies présentent-elles des décalages vers le rouge dans leurs spectres ? Quand vous étiez jeune et naïf, il y a quelques chapitres, c'était bien de discuter des décalages vers le rouge des galaxies lointaines comme s'ils résultaient de leur mouvement loin de nous. Mais maintenant que vous êtes un étudiant plus âgé et plus sage de la cosmologie, ce point de vue ne suffira tout simplement pas.
Une vision plus précise des décalages vers le rouge des galaxies est que les ondes lumineuses sont étirées par l'étirement de l'espace qu'elles traversent. Pensez à la lumière d'une galaxie lointaine. Lorsqu'elle s'éloigne de sa source, la lumière doit traverser l'espace. Si l'espace s'étire pendant tout le temps que la lumière se déplace, les ondes lumineuses seront également étirées. Un décalage vers le rouge est un étirement des ondes : la longueur d'onde de chaque onde augmente (Figure\(\PageIndex{1}\)). La lumière provenant de galaxies plus éloignées voyage plus longtemps que la lumière provenant de galaxies plus proches. Cela signifie que la lumière s'est étirée davantage que la lumière provenant de zones plus proches et présente donc un décalage vers le rouge plus important.
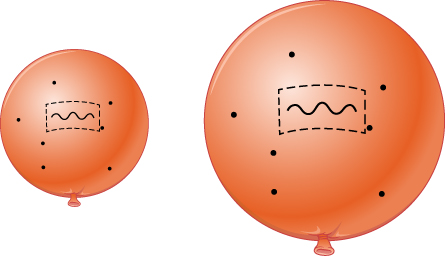
Ainsi, ce que le décalage vers le rouge mesuré de la lumière d'un objet nous indique à quel point l'univers s'est étendu depuis que la lumière a quitté l'objet. Si l'univers s'est agrandi d'un facteur 2, la longueur d'onde de la lumière (et de toutes les ondes électromagnétiques provenant de la même source) aura doublé.
Modèles de l'extension
Avant de connaître l'énergie noire ou d'avoir une bonne mesure de la quantité de matière présente dans l'univers, les astronomes ont élaboré des modèles spéculatifs sur la façon dont l'univers pourrait évoluer au fil du temps. Les quatre scénarios possibles sont présentés dans la figure\(\PageIndex{3}\). Dans ce diagramme, le temps avance du bas vers le haut et l'échelle de l'espace augmente à mesure que les cercles horizontaux s'élargissent.
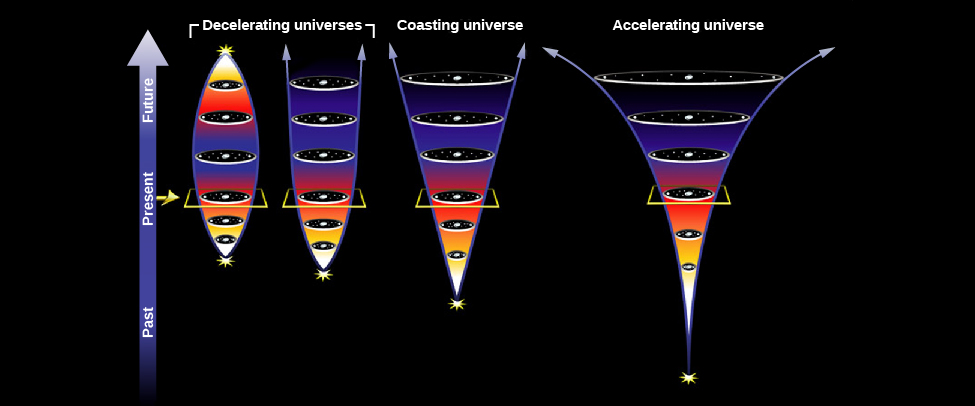
Le scénario le plus simple d'un univers en expansion serait celui où il\(R\) augmenterait avec le temps à un rythme constant. Mais vous savez déjà que la vie n'est pas si simple. L'univers contient une masse importante et sa gravité ralentit l'expansion, d'une grande quantité si l'univers contient beaucoup de matière, ou d'une quantité négligeable s'il est presque vide. Ensuite, il y a l'accélération observée, que les astronomes attribuent à une sorte d'énergie noire.
Explorons d'abord l'éventail des possibilités à l'aide de modèles pour différentes quantités de masse dans l'univers et pour différentes contributions de l'énergie noire. Dans certains modèles, comme nous le verrons, l'univers s'étend à jamais. Dans d'autres, elle cesse de s'étendre et commence à se contracter. Après avoir examiné les possibilités extrêmes, nous examinerons les observations récentes qui nous permettront de choisir le scénario le plus probable.
Nous devrions peut-être faire une pause pour constater à quel point il est remarquable de pouvoir y parvenir. Notre compréhension des principes qui sous-tendent le fonctionnement de l'univers à grande échelle et nos observations de la façon dont les objets de l'univers changent avec le temps nous permettent de modéliser l'évolution de l'ensemble du cosmos de nos jours. C'est l'une des plus grandes réussites de l'esprit humain.
Ce que les astronomes examinent en pratique, pour déterminer le type d'univers dans lequel nous vivons, c'est la densité moyenne de l'univers. Il s'agit de la masse de matière (y compris la masse d'énergie équivalente) 1 qui serait contenue dans chaque unité de volume (disons, 1 centimètre cube) si toutes les étoiles, galaxies et autres objets étaient démontés, atome par atome, et si toutes ces particules, ainsi que la lumière et les autres énergies, étaient répartis dans tout l'espace avec une uniformité absolue. Si la densité moyenne est faible, il y a moins de masse et moins de gravité, et l'univers ne ralentira pas beaucoup. Elle peut donc s'étendre à jamais. Une densité moyenne plus élevée, en revanche, signifie qu'il y a plus de masse et plus de gravité et que l'étirement de l'espace pourrait ralentir suffisamment pour que l'expansion finisse par cesser. Une densité extrêmement élevée pourrait même provoquer un nouvel effondrement de l'univers.
Pour un taux d'expansion donné, il existe une densité critique, c'est-à-dire la masse par unité de volume qui sera juste suffisante pour ralentir l'expansion jusqu'à zéro à un moment infini dans le futur. Si la densité réelle est supérieure à cette densité critique, l'expansion finira par s'inverser et l'univers commencera à se contracter. Si la densité réelle est plus faible, l'univers s'étendra pour toujours.
Ces différentes possibilités sont illustrées dans la figure\(\PageIndex{4}\). Dans ce graphique, l'un des plus complets de toutes les sciences, nous illustrons l'évolution de l'échelle de l'espace dans le cosmos en fonction du temps. Le temps augmente vers la droite et l'échelle de l'univers, R, augmente vers le haut sur la figure. Aujourd'hui, au point marqué « présent » sur l'axe temporel, R augmente dans chaque modèle. Nous savons que les galaxies s'éloignent actuellement les unes des autres, quel que soit le bon modèle. (Il en va de même pour une balle de baseball lancée haut en l'air. Bien qu'il puisse éventuellement retomber, c'est vers le début du lancer qu'il remonte le plus rapidement.)
Les différentes lignes qui parcourent le graphe correspondent à différents modèles de l'univers. La ligne droite en pointillés correspond à l'univers vide sans décélération ; elle intercepte l'axe du temps à la fois\(T_0\) (le temps de Hubble), dans le passé. Ce modèle n'est pas réaliste, mais il nous donne une mesure à laquelle comparer d'autres modèles. Les courbes situées sous la ligne pointillée représentent des modèles sans énergie noire et avec des décélérations variables, en commençant par le Big Bang à des moments plus courts dans le passé. La courbe au-dessus de la ligne pointillée montre ce qui se passe si l'expansion s'accélère. Regardons l'avenir de plus près en fonction des différents modèles.
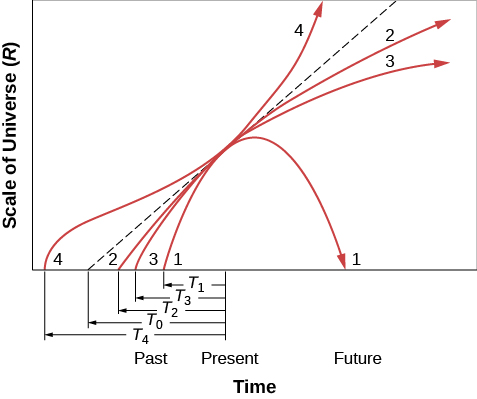
Commençons par la courbe 1 de la figure\(\PageIndex{4}\). Dans ce cas, la densité réelle de l'univers est supérieure à la densité critique et il n'y a pas d'énergie noire. Cet univers cessera de s'étendre dans le futur et commencera à se contracter. Ce modèle est appelé univers fermé et correspond à l'univers de gauche sur la Figure\(\PageIndex{3}\). Finalement, l'échelle tombe à zéro, ce qui signifie que l'espace sera réduit à une taille infiniment petite. Le célèbre physicien John Wheeler a qualifié cela de « grande crise », car la matière, l'énergie, l'espace et le temps seraient tous anéantis. Notez que le « big crunch » est à l'opposé du Big Bang : il s'agit d'une implosion. L'univers ne s'étend pas mais s'effondre sur lui-même.
Certains scientifiques ont émis l'hypothèse qu'un autre Big Bang pourrait suivre la crise, donnant lieu à une nouvelle phase d'expansion, puis à une autre contraction, oscillant peut-être entre des Big Bangs successifs et de grands craquements indéfiniment dans le passé et dans le futur. Ces spéculations étaient parfois appelées la théorie des oscillations de l'univers. Le défi pour les théoriciens était de savoir comment décrire la transition entre l'effondrement (lorsque l'espace et le temps eux-mêmes disparaissent) à l'expansion. Cependant, avec la découverte de l'énergie noire, il ne semble pas que l'univers connaisse une crise majeure. Nous pouvons donc passer au second plan de nos préoccupations à ce sujet.
Si la densité de l'univers est inférieure à la densité critique (courbe 2 sur la figure\(\PageIndex{4}\) et l'univers deuxième en partant de la gauche sur la figure\(\PageIndex{3}\)), la gravité n'est jamais assez importante pour arrêter l'expansion, et donc l'univers s'étend pour toujours. Un tel univers est infini et ce modèle est appelé univers ouvert. Le temps et l'espace commencent avec le Big Bang, mais ils n'ont pas de fin ; l'univers continue simplement de s'étendre, toujours un peu plus lentement au fil du temps. Les groupes de galaxies finissent par s'éloigner si loin qu'il serait difficile pour les observateurs de l'une d'entre elles de voir les autres. (Voir l'encadré sur À quoi pourrait ressembler l'univers dans un futur lointain ? plus loin dans la section pour en savoir plus sur le futur lointain dans les modèles d'univers fermé et ouvert.)
À la densité critique (courbe 3), l'univers peut à peine s'étendre pour toujours. L'univers à densité critique a un âge exactement des deux tiers\(T_0\), où se\(T_0\) situe l'âge de l'univers vide. Les univers qui commenceront un jour à se contracter ont moins des deux tiers d'âge\(T_0\).
Dans un univers vide (la figure en pointillés\(\PageIndex{4}\) et l'univers côtier dans la figure\(\PageIndex{3}\)), ni la gravité ni l'énergie noire ne sont suffisamment importantes pour affecter le taux d'expansion, qui est donc constant dans le temps.
Dans un univers à énergie noire, le rythme de l'expansion augmentera avec le temps, et l'expansion se poursuivra à un rythme toujours plus rapide. La courbe 4 de la figure\(\PageIndex{4}\), qui représente cet univers, a une forme complexe. Au début, lorsque la matière est très rapprochée, le taux d'expansion est le plus influencé par la gravité. L'énergie noire semble agir uniquement à grande échelle et devient donc plus importante à mesure que l'univers s'agrandit et que la matière commence à s'amincir. Dans ce modèle, l'univers ralentit d'abord, mais à mesure que l'espace s'étend, l'accélération joue un rôle plus important et l'expansion s'accélère.
Le bras de fer cosmique
Nous pourrions résumer notre discussion jusqu'ici en disant qu'un « bras de fer » se déroule dans l'univers entre les forces qui séparent tout et l'attraction gravitationnelle de la matière, qui réunit tout. Si nous pouvons déterminer qui va gagner ce bras de fer, nous apprendrons quel est le destin ultime de l'univers.
La première chose que nous devons savoir est la densité de l'univers. Est-elle supérieure, inférieure ou égale à la densité critique ? La densité critique dépend aujourd'hui de la valeur du taux d'expansion actuel\(H_0\). Si la constante de Hubble est d'environ 20 kilomètres/seconde par million d'années-lumière, la densité critique est d'environ\(10^{–26}\) kg/m 3. Voyons comment cette valeur se compare à la densité réelle de l'univers.
Exemple\(\PageIndex{1}\) : densité critique de l'univers
Comme nous l'avons vu, la densité critique est la combinaison de matière et d'énergie qui arrête le mouvement de l'univers à l'infini. Les équations d'Einstein conduisent à l'expression suivante pour la densité critique\( \left( \rho_{\text{crit}} \right) \) :
\[ \rho_{\text{crit}} = \frac{3H^2}{8 \pi G} \nonumber\]
où\(H\) est la constante de Hubble et\(G\) la constante universelle de la gravité\( \left( 6.67 \times 10^{–11} \text{ Nm}^2/ \text{kg}^2 \right)\).
Solution
Substituons nos valeurs et voyons ce que nous obtenons. Prenons un\(H = 22 \text{ km/s}\) par million d'années-lumière. Pour des raisons de cohérence, nous devons convertir les kilomètres et les années-lumière en mètres. Un million d'années-lumière =\(10^6 \times 9.5 \times 10^{15} \text{ m} = 9.5 \times 10^{21} \text{ m}\). Et\(22 \text{ km/s} = 2.2 \times 10^4 \text{ m/s}\). Cela fait\(H = 2.3 \times 10^{–18} ~ /\text{s}\) et\(H^2 = 5.36 \times 10^{–36} ~ /\text{s}^2\). Donc,
\[\rho_{\text{crit}} = \frac{3 \times 5.36 \times 10^{–36}}{8 \times 3.14 \times 6.67 \times 10^{–11}} = 9.6 \times 10^{–27} \text{ kg/m}^3 \nonumber\]
que nous pouvons compléter au\(10^{–26} \text{ kg/m}^3\). (Pour que les unités fonctionnent, vous devez savoir que\(N\) l'unité de force est la même que\(\text{kg} \times \text{m/s}^2\).)
Nous pouvons maintenant comparer les densités que nous mesurons dans l'univers à cette valeur critique. Notez que la densité est la masse par unité de volume, mais que l'énergie a une masse équivalente de\(m = E/c^2\) (d'après l'équation d'Einstein\(E = mc^2\)).
Exercice\(\PageIndex{1}\)
- Un seul grain de poussière a une masse d'environ\(1.1 \times 10^{–13} \text{ kg}\). Si la densité masse-énergie moyenne de l'espace est égale à la densité critique moyenne, combien d'espace serait nécessaire pour produire une énergie massique totale égale à un grain de poussière ?
- Si la constante de Hubble était le double de ce qu'elle est réellement, quelle serait la densité critique ?
- Réponse
-
- Dans ce cas, l'énergie massique moyenne dans un volume V de l'espace est E = ρ crit V. Ainsi, pour un espace à densité critique, nous exigeons que\[V= \frac{E_{\text{grain}}}{\rho_{\text{crit}}} = \frac{1.1 \times 10^{–13} \text{ kg}}{9.6 \times 10^{–26} \text{ kg/m}^3} = 1.15 \times 10^{12} \text{ m}^3 = (10,500 \text{ m})^3 \cong (10.5 \text{ km})^3 \nonumber\] les côtés d'un cube d'espace dont la densité d'énergie massique est en moyenne celle de la densité critique soient légèrement supérieurs à 10 km pour contenir l'énergie totale égale à un seul grain de poussière !
- Puisque la densité critique correspond au carré de la constante de Hubble, en doublant le paramètre de Hubble, la densité critique augmenterait d'un facteur quatre. Donc, si la constante de Hubble était de 44 km/s par million d'années-lumière au lieu de 22 km/s par million d'années-lumière, la densité critique serait\[\rho_{\text{crit}} = 4 \times 9.6 \times 10^{–27} \text{ kg/m}^3 = 3.8 \times 10^{–26} \text{ kg/m}^3. \nonumber\]
Nous pouvons commencer notre étude de la densité du cosmos en ignorant l'énergie noire et en estimant simplement la densité de toute la matière de l'univers, y compris la matière ordinaire et la matière noire. C'est là que le principe cosmologique est vraiment utile. Comme l'univers est le même partout (du moins à grande échelle), il suffit de mesurer la quantité de matière présente dans un (grand) échantillon représentatif de celui-ci. Cela est similaire à la manière dont une enquête représentative menée auprès de quelques milliers de personnes peut nous indiquer qui les millions de résidents des États-Unis préfèrent à la présidence.
Il existe plusieurs méthodes permettant de déterminer la densité moyenne de matière dans l'espace. L'une des méthodes consiste à compter toutes les galaxies à une distance donnée et à utiliser des estimations de leurs masses, y compris de la matière noire, pour calculer la densité moyenne. Ces estimations indiquent une densité d'environ 1\(1\) à\(2 \times 10^{–27} \text{ kg/m}^3\) (10 à 20 % de la densité critique), ce qui en soi est trop faible pour arrêter l'expansion.
Une grande partie de la matière noire se trouve en dehors des limites des galaxies, de sorte que cet inventaire n'est pas encore complet. Mais même si nous ajoutons une estimation de la matière noire à l'extérieur des galaxies, notre total ne dépassera pas environ 30 % de la densité critique. Nous définirons ces chiffres plus précisément plus loin dans ce chapitre, où nous inclurons également les effets de l'énergie noire.
Quoi qu'il en soit, même si nous ignorons l'énergie noire, il est prouvé que l'univers continuera de s'étendre pour toujours. La découverte de l'énergie noire qui accélère le taux d'expansion ne fait que renforcer cette conclusion. Les choses ne s'annoncent certainement pas bonnes pour les fans du modèle à univers fermé (Big Crunch).
à quoi pourrait ressembler l'univers dans un futur lointain ?
Certains disent que le monde finira dans le feu, d'autres dans la glace. D'après ce que j'ai goûté au désir, je le partage avec ceux qui sont favorables au feu. —Extrait du poème « Fire and Ice » de Robert Frost (1923)
Compte tenu du pouvoir destructeur de l'impact des astéroïdes, de l'expansion des géantes rouges et des supernovae voisines, notre espèce pourrait ne pas être présente dans un avenir lointain. Néanmoins, vous aimerez peut-être spéculer sur ce que ce serait de vivre dans un univers beaucoup plus ancien.
L'accélération observée laisse supposer que notre expansion se poursuivra dans un avenir indéfini. Si l'univers s'étend pour toujours (R augmente sans limite), les amas de galaxies s'étendront de plus en plus les uns des autres avec le temps. Au fil des siècles, l'univers deviendra plus mince, plus froid et plus sombre.
Dans chaque galaxie, les étoiles continueront de vivre leur vie et finiront par devenir des naines blanches, des étoiles à neutrons et des trous noirs. Les étoiles de faible masse peuvent mettre beaucoup de temps à terminer leur évolution, mais dans ce modèle, nous aurions littéralement tout le temps du monde. En fin de compte, même les naines blanches se refroidiront pour devenir des naines noires, toutes les étoiles à neutrons qui se révèlent être des pulsars cesseront lentement de tourner et les trous noirs dotés de disques d'accrétion achèveront un jour leur « repas ». Les restes d'étoiles seront tous sombres et difficiles à observer.
Cela signifie que la lumière qui nous révèle maintenant les galaxies finira par s'éteindre. Même si une petite poche de matière première était laissée dans un coin méconnu d'une galaxie, prête à être transformée en un nouvel amas d'étoiles, il suffira d'attendre que leur évolution soit également terminée. Et le temps est l'une des choses que ce modèle de l'univers possède. Il arrivera sûrement un moment où toutes les étoiles seront éteintes, où les galaxies seront aussi sombres que l'espace et où il ne restera plus aucune source de chaleur pour aider les êtres vivants à survivre. Les galaxies sans vie continueront alors à s'éloigner dans leur royaume sans lumière.
Si cette vision de l'avenir semble décourageante (d'un point de vue humain), gardez à l'esprit que nous ne comprenons fondamentalement pas pourquoi le taux d'expansion s'accélère actuellement. Ainsi, nos spéculations sur l'avenir ne sont que cela : des spéculations. Vous pourriez être rassuré de savoir que la science est toujours un rapport de progrès. Les idées les plus avancées sur l'univers datant d'il y a cent ans nous semblent aujourd'hui plutôt primitives. Il se peut fort bien que nos meilleurs modèles d'aujourd'hui paraîtront également dans cent ou mille ans un peu simplistes et qu'il existe d'autres facteurs qui déterminent le destin ultime de l'univers dont nous ignorons encore totalement l'existence.
Âges de galaxies lointaines
Dans le chapitre sur les galaxies, nous avons discuté de la manière dont nous pouvons utiliser la loi de Hubble pour mesurer la distance par rapport à une galaxie. Mais cette méthode simple ne fonctionne qu'avec des galaxies qui ne sont pas trop éloignées. Une fois que nous atteignons de grandes distances, nous regardons si loin dans le passé que nous devons tenir compte de l'évolution du taux d'expansion de l'univers. Comme nous ne pouvons pas mesurer ces changements directement, nous devons supposer que l'un des modèles de l'univers est capable de convertir de grands décalages vers le rouge en distances.
C'est pourquoi les astronomes se tortillent lorsque des journalistes et des étudiants leur demandent exactement à quelle distance se trouve un quasar ou une galaxie lointain récemment découvert. Nous ne pouvons vraiment pas donner de réponse sans d'abord expliquer le modèle de l'univers que nous supposons pour le calculer (moment auquel un journaliste ou un étudiant est parti ou dort depuis longtemps). Plus précisément, nous devons utiliser un modèle qui inclut l'évolution du taux d'expansion au fil du temps. Les principaux ingrédients du modèle sont les quantités de matière, y compris la matière noire, et la masse équivalente (selon\(E = mc^2\)) de l'énergie noire ainsi que la constante de Hubble.
Ailleurs dans ce livre, nous avons estimé la densité de masse de la matière ordinaire et de la matière noire à environ 0,3 fois la densité critique, et l'équivalent massique de l'énergie noire à environ 0,7 fois la densité critique. Nous appellerons ces valeurs le « modèle standard de l'univers ». Les dernières estimations (légèrement améliorées) de ces valeurs et leurs preuves seront présentées plus loin dans ce chapitre. Les calculs nécessitent également la valeur actuelle de la constante de Hubble. Pour le tableau\(\PageIndex{1}\), nous avons adopté une constante de Hubble de 67,3 kilomètres/seconde/million de parsecs (plutôt que de l'arrondir à 70 kilomètres/seconde/million de parsecs), ce qui correspond à l'âge de 13,8 milliards d'années de l'univers estimé par les dernières observations.
Une fois que nous avons supposé un modèle, nous pouvons l'utiliser pour calculer l'âge de l'univers au moment où un objet a émis la lumière que nous voyons. À titre d'exemple, le tableau\(\PageIndex{1}\) répertorie les heures pendant lesquelles la lumière a été émise par des objets présentant différents décalages vers le rouge en tant que fractions de l'âge actuel de l'univers. Les temps sont donnés pour deux modèles très différents afin que vous puissiez avoir une idée du fait que les âges calculés sont assez similaires. Le premier modèle suppose que l'univers possède une densité critique de matière et aucune énergie noire. Le second modèle est le modèle standard décrit dans le paragraphe précédent. La première colonne du tableau est le décalage vers le rouge, qui est donné par l'équation z = Δλ/λ0 et qui est une mesure de la mesure dans laquelle la longueur d'onde de la lumière a été étirée par l'expansion de l'univers au cours de son long voyage vers nous.
| Redshift | Pourcentage de l'âge actuel de l'univers où la lumière a été émise (masse = densité critique) | Pourcentage de l'âge actuel de l'univers où la lumière a été émise (masse = 0,3 densité critique ; énergie noire = 0,7 densité critique) |
|---|---|---|
| 0 | 100 (maintenant) | 100 (maintenant) |
| 0,5 | 54 | 63 |
| 1,0 | 35 | 43 |
| 2,0 | 19 | 24 |
| 3,0 | 13 | 16 |
| 4,0 | 9 | 11 |
| 5,0 | 7 | 9 |
| 8,0 | 4 | 5 |
| 11,9 | 2.1 | 2.7 |
| Infini | 0 | 0 |
Remarquez qu'à mesure que nous trouvons des objets dont les décalages vers le rouge sont de plus en plus élevés, nous nous tournons vers des fractions de plus en plus petites de l'âge de l'univers. Les décalages vers le rouge les plus élevés observés au moment de la rédaction de ce livre sont proches de 12 (Figure\(\PageIndex{5}\)). Comme le\(\PageIndex{1}\) montre le tableau, nous voyons ces galaxies telles qu'elles étaient lorsque l'univers n'était qu'environ 3 % plus âgé qu'aujourd'hui. Ils ne s'étaient déjà formés qu'environ 700 millions d'années après le Big Bang.

Résumé
Pour décrire les propriétés à grande échelle de l'univers, un modèle isotrope et homogène (le même partout) est une assez bonne approximation de la réalité. L'univers est en expansion, ce qui signifie que l'univers subit un changement d'échelle avec le temps ; l'espace s'étend et les distances augmentent du même facteur partout à un moment donné. Les observations montrent que la densité de masse de l'univers est inférieure à la densité critique. En d'autres termes, il n'y a pas assez de matière dans l'univers pour arrêter l'expansion. Avec la découverte de l'énergie noire, qui accélère le taux d'expansion, les preuves observationnelles montrent clairement que l'univers s'étendra pour toujours. Les observations indiquent que l'expansion a commencé il y a environ 13,8 milliards d'années.
Notes
1 Par masse équivalente, nous entendons ce qui résulterait si l'énergie était transformée en masse selon la formule d'Einstein,\(E = mc^2\).
Lexique
- univers fermé
- un modèle dans lequel l'univers s'étend à partir d'un Big Bang, s'arrête, puis se contracte jusqu'à un grand moment
- densité critique
- en cosmologie, la densité juste suffisante pour arrêter l'expansion de l'univers après un temps infini
- univers ouvert
- un modèle dans lequel la densité de l'univers n'est pas assez élevée pour arrêter l'expansion de l'univers


