29.1 : L'ère de l'univers
- Page ID
- 192387
Objectifs d'apprentissage
À la fin de cette section, vous serez en mesure de :
- Décrivez comment nous estimons l'âge de l'univers
- Expliquer comment les variations du taux d'expansion au fil du temps influent sur les estimations de l'âge de l'univers
- Décrivez les preuves que l'énergie noire existe et que le taux d'expansion s'accélère actuellement
- Décrivez certaines preuves indépendantes de l'âge de l'univers qui sont cohérentes avec l'estimation de l'âge basée sur le taux d'expansion
Pour explorer l'histoire de l'univers, nous suivrons la même voie que celle que les astronomes ont suivie historiquement, en commençant par étudier l'univers voisin, puis en sondant des objets de plus en plus éloignés et en regardant plus loin dans le temps.
La prise de conscience que l'univers change avec le temps s'est faite dans les années 1920 et 1930, lorsque les mesures des décalages vers le rouge d'un large échantillon de galaxies sont devenues disponibles. Avec le recul, il est surprenant que les scientifiques aient été si choqués de découvrir que l'univers était en expansion. En fait, nos théories de la gravité exigent que l'univers soit en expansion soit en contraction. Pour montrer ce que nous voulons dire, commençons par un univers de taille limitée, disons une boule géante de mille galaxies. Toutes ces galaxies s'attirent les unes les autres à cause de leur gravité. S'ils étaient initialement immobiles, ils commenceraient inévitablement à se rapprocher et finiraient par entrer en collision. Ils ne pouvaient éviter cet effondrement que s'ils s'éloignaient l'un de l'autre à grande vitesse pour une raison ou une autre. De la même manière, ce n'est que si une fusée est lancée à une vitesse suffisante qu'elle peut éviter de retomber sur Terre.
Le problème de ce qui se passe dans un univers infini est plus difficile à résoudre, mais Einstein (et d'autres) a utilisé sa théorie de la relativité générale (que nous avons décrite dans Black Holes and Curved Spacetime) pour montrer que même les univers infinis ne peuvent pas être statiques. Comme les astronomes de l'époque ne savaient pas encore que l'univers était en expansion (et qu'Einstein lui-même n'était pas philosophiquement disposé à accepter un univers en mouvement), il a modifié ses équations en introduisant un nouveau terme arbitraire (on pourrait l'appeler un facteur de fudge) appelé constante cosmologique . Cette constante représentait une force de répulsion hypothétique qui pourrait équilibrer l'attraction gravitationnelle sur les plus grandes échelles et permettre aux galaxies de rester à des distances fixes les unes des autres. Ainsi, l'univers pourrait rester immobile.
Environ dix ans plus tard, Hubble et ses collègues ont rapporté que l'univers était en expansion, de sorte qu'aucune force d'équilibre mystérieuse n'était nécessaire. (Nous en avons discuté dans le chapitre sur les galaxies.) Einstein aurait déclaré que l'introduction de la constante cosmologique était « la plus grosse erreur de ma vie ». Comme nous le verrons plus loin dans ce chapitre, des observations relativement récentes indiquent toutefois que l'expansion s'accélère. Des observations sont actuellement effectuées pour déterminer si cette accélération est compatible avec une constante cosmologique. D'une certaine manière, il se peut qu'Einstein ait eu raison après tout.
Visionnez cette exposition Web sur l'histoire de notre réflexion sur la cosmologie, avec des images et des biographies, présentée par le Centre d'histoire de la physique de l'American Institute of Physics.
L'heure de Hubble
Si nous avions un film sur l'univers en pleine expansion et que nous le regardions à rebours, que verrions-nous ? Les galaxies, au lieu de s'éloigner, se déplaceraient ensemble dans notre film, se rapprochant de plus en plus. Finalement, nous avons découvert que toute la matière que nous pouvons voir aujourd'hui était autrefois concentrée dans un volume infinitésimal. Les astronomes identifient cette époque au début de l'univers. L'explosion de cet univers concentré au début des temps s'appelle le Big Bang (ce n'est pas un mauvais terme, puisqu'on ne peut pas avoir de plus grand bruit qu'un qui crée l'univers entier). Mais quand est-ce que cette explosion s'est produite ?
Nous pouvons faire une estimation raisonnable du temps écoulé depuis le début de l'expansion universelle. Pour voir comment les astronomes s'y prennent, commençons par une analogie. Supposons que votre classe d'astronomie décide d'organiser une fête (une sorte de « Big Bang ») chez quelqu'un pour célébrer la fin du semestre. Malheureusement, tout le monde fait la fête avec tant d'enthousiasme que les voisins appellent la police, qui arrive et renvoie tout le monde au même moment. Vous rentrez chez vous à 2 heures du matin, encore un peu bouleversé par la façon dont la fête s'est terminée, et vous réalisez que vous avez oublié de regarder votre montre pour savoir à quelle heure la police est arrivée. Mais vous utilisez une carte pour mesurer que la distance entre la fête et votre maison est de 40 kilomètres. Et vous vous souvenez également que vous avez fait tout le trajet à une vitesse constante de 80 kilomètres/heure (car vous vous inquiétiez des voitures de police qui vous suivaient). Par conséquent, le voyage doit avoir pris :
\[ \text{time} = \frac{\text{distance}}{\text{velocity}} = \frac{40 \text{ kilometers}}{80 \text{ kilometers/hour}} = 0.5 \text{ hours} \nonumber\]
La fête a donc dû se terminer à 1 h 30 du matin.
Aucun être humain n'était là pour regarder ses montres lorsque l'univers a commencé, mais nous pouvons utiliser la même technique pour estimer le moment où les galaxies ont commencé à s'éloigner les unes des autres. (N'oubliez pas qu'en réalité, c'est l'espace qui s'étend, et non les galaxies qui se déplacent dans l'espace statique.) Si nous pouvons mesurer la distance entre les galaxies actuellement et la vitesse à laquelle elles se déplacent, nous pouvons déterminer la durée du voyage.
Appelons l'âge de l'univers ainsi mesuré T 0. Commençons par un cas simple en supposant que l'expansion a été constante depuis le début de l'expansion de l'univers. Dans ce cas, le temps qu'il a fallu à une galaxie pour s'éloigner d'une distance, d, de la Voie lactée (rappelez-vous qu'au début, les galaxies formaient un tout petit volume) est (comme dans notre exemple)
\[T_0=d/v \nonumber\]
où\(v\) est la vitesse de la galaxie. Si nous pouvons mesurer la vitesse à laquelle les galaxies s'éloignent, ainsi que les distances qui les séparent, nous pouvons établir depuis combien de temps l'expansion a commencé.
Faire de telles mesures devrait vous sembler très familier. C'est exactement ce que Hubble et de nombreux astronomes ont dû faire après lui pour établir la loi de Hubble et la constante de Hubble. Nous avons appris dans Galaxies que la distance et la vitesse d'une galaxie dans l'univers en expansion sont liées par
\[V=H \times d \nonumber\]
où\(H\) est la constante de Hubble. La combinaison de ces deux expressions nous donne
\[T_0= \frac{d}{v} = \frac{d}{(H \times d)} = \frac{1}{H} \nonumber\]
Nous voyons donc que le travail de calcul de ce temps était déjà fait pour nous lorsque les astronomes ont mesuré la constante de Hubble. L'âge de l'univers ainsi estimé s'avère être juste l'inverse de la constante de Hubble (c'est-à-dire 1/\(H\)). Cette estimation de l'âge est parfois appelée temps de Hubble. Pour une constante de Hubble de 20 kilomètres/seconde par million d'années-lumière, le temps de Hubble est d'environ 15 milliards d'années. L'unité utilisée par les astronomes pour la constante de Hubble est le kilomètre/seconde par million de parsecs. Dans ces unités, la constante de Hubble est égale à environ 70 kilomètres/seconde par million de parsecs, toujours avec une incertitude d'environ 5 %.
Pour que les chiffres soient plus faciles à retenir, nous avons arrondi les chiffres ici. Les estimations de la constante de Hubble sont en fait plus proches de 21 ou 22 kilomètres/seconde par million d'années-lumière, ce qui rapprocherait l'âge de 14 milliards d'années. Mais il existe toujours une incertitude d'environ 5 % dans la constante de Hubble, ce qui signifie que l'âge de l'univers estimé de cette manière est également incertain d'environ 5 %.
Pour mettre ces incertitudes en perspective, sachez toutefois qu'il y a 50 ans, l'incertitude était un facteur de 2. Des progrès remarquables ont été réalisés au cours des deux dernières décennies en vue de déterminer la constante de Hubble.
Le rôle de la décélération
Le temps de Hubble n'est le bon âge pour l'univers que si le taux d'expansion a été constant depuis le début de l'expansion de l'univers. Pour poursuivre notre analogie entre les fêtes de fin de semestre et les fêtes, cela revient à supposer que vous êtes rentré chez vous à un rythme constant, alors qu'en fait, cela n'a peut-être pas été le cas. Au début, furieux de devoir partir, vous avez peut-être roulé vite, mais ensuite, en vous calmant et en pensant aux voitures de police sur l'autoroute, vous avez peut-être commencé à ralentir jusqu'à ce que vous conduisiez à une vitesse plus socialement acceptable (80 kilomètres/heure par exemple). Dans ce cas, étant donné que vous conduisiez plus vite au départ, le trajet pour rentrer chez vous aurait pris moins d'une demi-heure.
De la même manière, en calculant le temps de Hubble, nous avons supposé que H a été constant pendant tout le temps. Il s'avère que ce n'est pas une bonne hypothèse. Plus tôt dans leur réflexion à ce sujet, les astronomes s'attendaient à ce que le taux d'expansion ralentisse. Nous savons que la matière crée la gravité, par laquelle tous les objets tirent sur tous les autres objets. L'attraction mutuelle entre les galaxies devait ralentir l'expansion au fil du temps. Cela signifie que, si la gravité était la seule force agissant (un gros si, comme nous le verrons dans la section suivante), alors le taux d'expansion aurait dû être plus rapide dans le passé qu'il ne l'est aujourd'hui. Dans ce cas, on dirait que l'univers ralentit depuis le début.
Le degré de décélération dépend de l'importance de la gravité pour ralentir l'expansion. Si l'univers était presque vide, le rôle de la gravité serait mineur. La décélération serait alors proche de zéro et l'univers se serait développé à un rythme constant. Mais dans un univers où la densité de matière est importante, l'attraction de la gravité signifie que le taux d'expansion devrait être plus lent aujourd'hui qu'auparavant. Si nous utilisons le taux d'expansion actuel pour estimer le temps qu'il a fallu aux galaxies pour atteindre leurs séparations actuelles, nous surestimerons l'âge de l'univers, tout comme nous avons peut-être surestimé le temps qu'il vous a fallu pour rentrer chez vous après la fête.
Une accélération universelle
Les astronomes ont passé plusieurs décennies à chercher des preuves du ralentissement de l'expansion, mais ils n'y sont pas parvenus. Il leur fallait 1) de plus grands télescopes pour mesurer les décalages vers le rouge de galaxies plus éloignées et 2) une ampoule standard très lumineuse (ou une bougie standard), c'est-à-dire un objet astronomique dont la luminosité est connue et qui produit une énorme quantité d'énergie et peut être observé à distance. d'un milliard d'années-lumière ou plus.
Rappelons que nous avons discuté des ampoules standard dans le chapitre sur les galaxies. Si nous comparons la luminosité d'une ampoule standard et son intensité réelle dans nos télescopes, la différence nous permet de calculer sa distance. Le décalage vers le rouge de la galaxie dans laquelle se trouve une telle ampoule peut nous indiquer à quelle vitesse elle se déplace dans l'univers. Nous pouvons donc mesurer sa distance et son mouvement indépendamment.
Ces deux exigences ont finalement été satisfaites dans les années 1990. Les astronomes ont montré que les supernovae de type Ia (voir La mort des étoiles), avec certaines corrections basées sur la forme de leurs courbes lumineuses, sont des ampoules standard. Ce type de supernova se produit lorsqu'une naine blanche accréte suffisamment de matière provenant d'une étoile compagne pour dépasser la limite de Chandrasekhar, puis s'effondre et explose. Au moment où la luminosité est maximale, ces supernovae spectaculaires peuvent brièvement éclipser les galaxies qui les hébergent et peuvent donc être observées à de très grandes distances. De grands télescopes de 8 à 10 mètres peuvent être utilisés pour obtenir les spectres nécessaires pour mesurer les décalages vers le rouge des galaxies hôtes (Figure\(\PageIndex{2}\)).
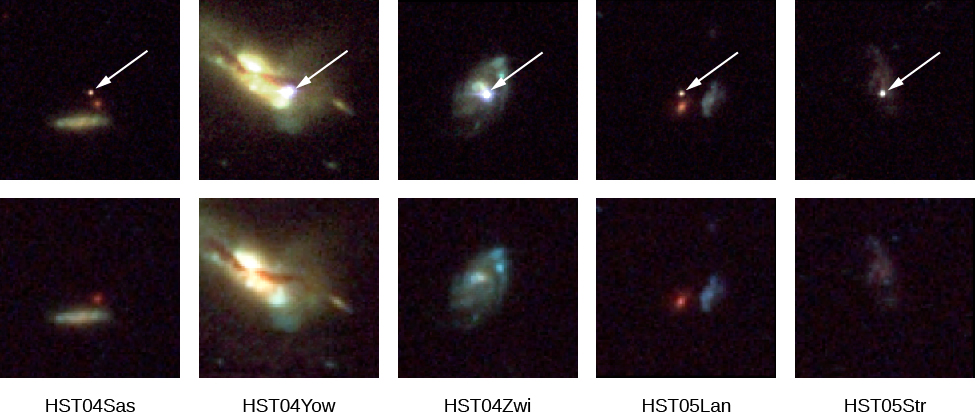
Le résultat d'une étude minutieuse et minutieuse de ces supernovae dans diverses galaxies, menée par deux groupes de chercheurs, a été publié en 1998. C'était choquant et tellement révolutionnaire que leur découverte a reçu le prix Nobel de physique 2011. Les chercheurs ont découvert que ces supernovae de type Ia présentes dans des galaxies lointaines étaient plus faibles que prévu selon la loi de Hubble, compte tenu des décalages vers le rouge mesurés de leurs galaxies hôtes. En d'autres termes, les distances estimées à partir des supernovae utilisées comme ampoules standard ne correspondaient pas aux distances mesurées à partir des décalages vers le rouge.
Si l'univers décélérait, on pourrait s'attendre à ce que les supernovae lointaines soient plus lumineuses que prévu. Le ralentissement les aurait rapprochés de nous. Au lieu de cela, ils étaient plus faibles, ce qui semblait au début n'avoir aucun sens.
Avant d'accepter cette évolution choquante, les astronomes ont d'abord exploré la possibilité que les supernovae ne soient pas vraiment aussi utiles que les ampoules classiques qu'ils le pensaient. Peut-être que les supernovae semblaient trop faibles parce que la poussière qui se trouvait le long de notre champ de vision absorbait une partie de leur lumière. Ou peut-être que les supernovae situées à de grandes distances étaient, pour une raison ou une autre, intrinsèquement moins lumineuses que les supernovae voisines de type Ia.
De nombreuses observations plus détaillées ont écarté ces possibilités. Les scientifiques ont ensuite dû envisager l'alternative selon laquelle la distance estimée à partir du décalage vers le rouge était incorrecte. Les distances dérivées des décalages vers le rouge supposent que la constante de Hubble a toujours été vraiment constante. Nous avons vu que l'une des raisons pour lesquelles cela pourrait ne pas être constant est que l'expansion ralentit. Mais supposons qu'aucune des deux hypothèses ne soit correcte (vitesse constante ou ralentissement).
Supposons plutôt que l'univers accélère. Si l'univers s'étend plus rapidement aujourd'hui qu'il ne l'était il y a des milliards d'années, notre éloignement des supernovae lointaines s'est accéléré depuis l'explosion, nous éloignant de plus en plus d'elles. La lumière de l'explosion doit parcourir une plus grande distance pour nous atteindre que si le taux d'expansion était constant. Plus la lumière se déplace loin, plus elle paraît faible. Cette conclusion expliquerait les observations des supernovas de manière naturelle, et cela a maintenant été confirmé par de nombreuses autres observations au cours des deux dernières décennies. Il semble vraiment que l'expansion de l'univers s'accélère, une idée tellement inattendue que les astronomes ont d'abord résisté à l'envisager.
Comment l'expansion de l'univers peut-elle s'accélérer ? Si vous souhaitez accélérer votre voiture, vous devez fournir de l'énergie en appuyant sur l'accélérateur. De même, de l'énergie doit être fournie pour accélérer l'expansion de l'univers. La découverte de l'accélération a été choquante car les scientifiques n'ont toujours aucune idée de la source de l'énergie. Les scientifiques appellent ce que c'est l'énergie noire, ce qui montre clairement à quel point nous la comprenons peu.
Notez que cette nouvelle composante de l'univers n'est pas la matière noire dont nous avons parlé dans les chapitres précédents. L'énergie noire est une autre chose que nous n'avons pas encore détectée dans nos laboratoires sur Terre.
Qu'est-ce que l'énergie noire ? L'une des possibilités est qu'il s'agit de la constante cosmologique, qui est une énergie associée au vide de l'espace « vide » lui-même. La mécanique quantique (l'intrigante théorie du comportement des choses aux niveaux atomique et subatomique) nous apprend que la source de cette énergie du vide pourrait être de minuscules particules élémentaires qui entrent et sortent de l'existence partout dans l'univers. Diverses tentatives ont été faites pour calculer l'ampleur des effets de cette énergie du vide, mais ces tentatives n'ont pas abouti jusqu'à présent. En fait, l'ordre de grandeur des estimations théoriques de l'énergie du vide basées sur la mécanique quantique de la matière et la valeur requise pour rendre compte de l'accélération de l'expansion de l'univers diffèrent d'un facteur incroyable d'au moins 10120 (soit un 1 suivi de 120 zéros) ! Diverses autres théories ont été avancées, mais l'essentiel est que, bien qu'il existe des preuves irréfutables de l'existence de l'énergie noire, nous ne connaissons pas encore la source de cette énergie.
Quelle que soit l'énergie noire, il convient de noter que la découverte que le taux d'expansion n'a pas été constant depuis le début de l'univers complique le calcul de l'âge de l'univers. Il est intéressant de noter que l'accélération ne semble pas avoir commencé avec le Big Bang. Au cours des premiers milliards d'années qui ont suivi le Big Bang, lorsque les galaxies étaient proches les unes des autres, la gravité était suffisamment forte pour ralentir l'expansion. À mesure que les galaxies s'éloignaient, l'effet de la gravité s'affaiblissait. Plusieurs milliards d'années après le Big Bang, l'énergie noire a pris le dessus et l'expansion a commencé à s'accélérer (Figure\(\PageIndex{3}\)).
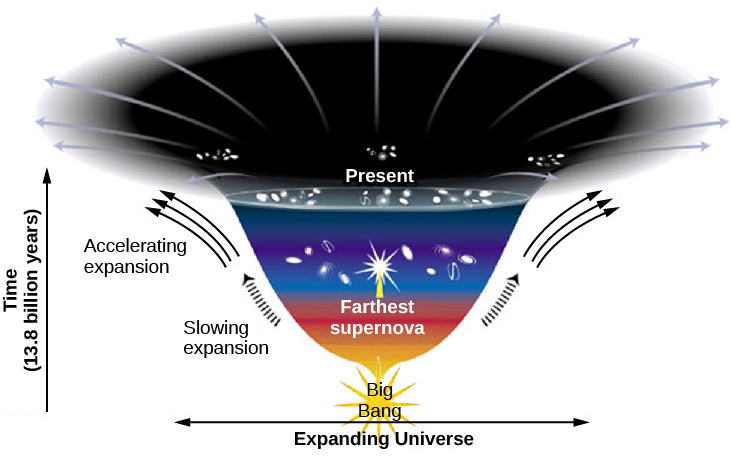
La décélération fait en sorte que l'âge de l'univers estimé par la simple relation\(T_0 = 1/H\) semble plus ancien qu'il ne l'est réellement, tandis que l'accélération agit pour le rendre plus jeune. Par une heureuse coïncidence, nos meilleures estimations de l'ampleur de la décélération et de l'accélération ont permis d'obtenir une réponse pour l'âge très proche de\(T_0 = 1/H\). La meilleure estimation actuelle est que l'univers a 13,8 milliards d'années avec une incertitude d'environ 100 millions d'années seulement.
Tout au long de ce chapitre, nous avons fait référence à la constante de Hubble. Nous savons maintenant que la constante de Hubble change avec le temps. Elle est cependant constante partout dans l'univers et à tout moment. Lorsque nous disons que la constante de Hubble est d'environ 70 kilomètres/seconde/million de parsecs, nous voulons dire que c'est la valeur de la constante de Hubble à l'heure actuelle.
Comparaison des âges
Nous avons maintenant une estimation de l'âge de l'univers à partir de son expansion. Cette estimation est-elle cohérente avec d'autres observations ? Par exemple, les étoiles ou autres objets astronomiques les plus anciens sont-ils âgés de moins de 13,8 milliards d'années ? Après tout, l'univers doit être au moins aussi vieux que ses objets les plus anciens.
Dans notre Galaxie et dans d'autres, les étoiles les plus anciennes se trouvent dans les amas globulaires (Figure\(\PageIndex{4}\)), qui peuvent être datés à l'aide des modèles d'évolution stellaire décrits dans le chapitre Les étoiles de l'adolescence à la vieillesse.

La précision des estimations de l'âge des amas globulaires s'est nettement améliorée ces dernières années pour deux raisons. Tout d'abord, les modèles de l'intérieur des amas d'étoiles globulaires ont été améliorés, principalement grâce à de meilleures informations sur la façon dont les atomes absorbent le rayonnement lorsqu'ils se déplacent du centre d'une étoile vers l'espace. Deuxièmement, les observations par satellite ont amélioré la précision de nos mesures des distances par rapport à ces clusters. La conclusion est que les étoiles les plus anciennes se sont formées il y a environ 12 à 13 milliards d'années.
Cette estimation de l'âge a récemment été confirmée par l'étude du spectre de l'uranium dans les étoiles. L'isotope d'uranium 238 est radioactif et se désintègre (se transforme en un autre élément) au fil du temps. (L'uranium 238 reçoit sa désignation parce qu'il possède 92 protons et 146 neutrons.) Nous savons (grâce à la façon dont les étoiles et les supernovae fabriquent les éléments) quelle quantité d'uranium 238 est généralement produite par rapport aux autres éléments. Supposons que nous mesurions la quantité d'uranium par rapport aux éléments non radioactifs dans une très vieille étoile et dans notre propre Soleil, et que nous comparions les abondances. Grâce à ces informations, nous pouvons estimer combien de temps l'uranium se désintègre dans la très vieille étoile, car nous savons grâce à notre propre Soleil combien d'uranium se désintègre en 4,5 milliards d'années.
La lignée d'uranium est très faible et difficile à distinguer, même dans le Soleil, mais elle a maintenant été mesurée dans une étoile extrêmement ancienne à l'aide du très grand télescope européen (Figure\(\PageIndex{5}\)). En comparant l'abondance avec celle du système solaire, dont nous connaissons l'âge, les astronomes estiment que l'étoile a 12,5 milliards d'années, avec une incertitude d'environ 3 milliards d'années. Bien que l'incertitude soit grande, ces travaux constituent une confirmation importante des âges estimés par les études des amas d'étoiles globulaires. Il convient de noter que l'estimation de l'âge de l'uranium est totalement indépendante ; elle ne dépend ni de la mesure des distances ni de modèles de l'intérieur des étoiles.

Comme nous le verrons plus loin dans ce chapitre, les amas d'étoiles globulaires ne se sont probablement pas formés avant que l'expansion de l'univers ne soit en cours depuis au moins quelques centaines de millions d'années. En conséquence, leur âge est conforme à l'âge de 13,8 milliards d'années estimé à partir du taux d'expansion.
Résumé
La cosmologie est l'étude de l'organisation et de l'évolution de l'univers. L'univers est en expansion, et c'est l'un des principaux points de départ observationnels des théories cosmologiques modernes. Les observations modernes montrent que le taux d'expansion n'a pas été constant tout au long de la vie de l'univers. Au départ, lorsque les galaxies étaient proches les unes des autres, les effets de la gravité étaient plus forts que ceux de l'énergie noire, et le taux d'expansion ralentissait progressivement. À mesure que les galaxies s'éloignaient, l'influence de la gravité sur le taux d'expansion s'affaiblissait. Les mesures de supernovae éloignées montrent que lorsque l'univers avait environ la moitié de son âge actuel, l'énergie noire a commencé à dominer le taux d'expansion et à l'accélérer. Pour estimer l'âge de l'univers, il faut tenir compte des variations du taux d'expansion. Après avoir tenu compte de ces effets, les astronomes estiment que toute la matière de l'univers observable était concentrée dans un très petit volume il y a 13,8 milliards d'années, une époque que nous appelons le Big Bang.
Lexique
- Big Bang
- la théorie de la cosmologie selon laquelle l'expansion de l'univers a commencé par une explosion primitive (de l'espace, du temps, de la matière et de l'énergie)
- constante cosmologique
- terme utilisé dans les équations de la relativité générale qui représente une force répulsive dans l'univers
- cosmologie
- l'étude de l'organisation et de l'évolution de l'univers
- énergie noire
- l'énergie qui provoque l'accélération de l'expansion de l'univers ; son existence est déduite de l'observation de supernovae distantes


