26.5 : L'univers en expansion
- Page ID
- 192203
Objectifs d'apprentissage
À la fin de cette section, vous serez en mesure de :
- Décrivez la découverte selon laquelle les galaxies s'éloignent à mesure que l'univers évolue
- Expliquer comment utiliser la loi de Hubble pour déterminer les distances par rapport à des galaxies éloignées
- Décrire des modèles de la nature d'un univers en expansion
- Expliquer la variation de la constante de Hubble
Nous arrivons maintenant à l'une des découvertes les plus importantes jamais faites en astronomie : l'expansion de l'univers. Avant de décrire comment cette découverte a été faite, il convient de souligner que les premières étapes de l'étude des galaxies ont eu lieu à une époque où les techniques de spectroscopie faisaient également de grands progrès. Les astronomes utilisant de grands télescopes pouvaient enregistrer le spectre d'une étoile ou d'une galaxie faible sur des plaques photographiques, en guidant leurs télescopes de manière à ce qu'ils restent pointés vers le même objet pendant de nombreuses heures et collectent plus de lumière. Les spectres de galaxies obtenus contenaient une mine d'informations sur la composition de la galaxie et les vitesses de ces grands systèmes stellaires.
Les observations pionnières de Slipher
Curieusement, la découverte de l'expansion de l'univers a commencé par la recherche de Martiens et d'autres systèmes solaires. En 1894, l'astronome controversé (et riche) Percival Lowell a créé un observatoire à Flagstaff, en Arizona, pour étudier les planètes et rechercher la vie dans l'univers. Lowell pensait que les nébuleuses spirales pouvaient être des systèmes solaires en cours de formation. Il a donc demandé à l'un des jeunes astronomes de l'observatoire, Veto M. Slipher (Figure\(\PageIndex{1}\)), de photographier les spectres de certaines nébuleuses spirales afin de voir si leurs raies spectrales pouvaient présenter des compositions chimiques similaires à celles attendues pour les planètes nouvellement formées.

Le principal instrument de l'observatoire Lowell était un télescope à réfraction de 24 pouces, qui n'était pas du tout bien adapté à l'observation de nébuleuses spirales de faible intensité. Avec la technologie disponible à cette époque, les plaques photographiques devaient être exposées pendant 20 à 40 heures pour produire un bon spectre (dans lequel les positions des raies pouvaient révéler le mouvement d'une galaxie). Cela impliquait souvent de continuer à exposer la même photographie pendant plusieurs nuits. À partir de 1912 et en déployant des efforts héroïques sur une période d'environ 20 ans, Slipher a réussi à photographier les spectres de plus de 40 nébuleuses spirales (qui se sont toutes révélées être des galaxies).
À sa grande surprise, les raies spectrales de la plupart des galaxies présentaient un décalage vers le rouge étonnant. Par « décalage vers le rouge », nous entendons que les raies des spectres sont déplacées vers des longueurs d'onde plus longues (vers l'extrémité rouge du spectre visible). Souvenez-vous du chapitre sur le rayonnement et les spectres qu'un décalage vers le rouge est observé lorsque la source des ondes s'éloigne de nous. Les observations de Slipher ont montré que la plupart des spirales s'élancent à des vitesses énormes ; la vitesse maximale qu'il a mesurée était de 1 800 kilomètres par seconde.
Seules quelques spirales, telles que les galaxies d'Andromède et du Triangle et M81, qui sont désormais connues pour être nos proches voisines, se sont révélées s'approcher de nous. Toutes les autres galaxies s'éloignaient. Slipher a annoncé cette découverte pour la première fois en 1914, des années avant que Hubble ne montre que ces objets étaient d'autres galaxies et avant que quiconque ne sache à quelle distance ils se trouvaient. À l'époque, personne ne savait vraiment quoi penser de cette découverte.
Loi de Hubble
Les profondes implications du travail de Slipher ne sont apparues que dans les années 1920. Georges Lemaître était un prêtre belge et un astronome de formation. En 1927, il a publié un article en français dans un journal belge obscur dans lequel il suggérait que nous vivions dans un univers en pleine expansion. Le titre de l'article (traduit en anglais) est « A Homogen Universe of Constant Mass and Growing Radius Accounting for the Radial Velocity of Extragalactic Nebulae ». Lemaître avait découvert que les équations de la relativité d'Einstein étaient compatibles avec un univers en expansion (comme l'avait fait indépendamment le scientifique russe Alexander Friedmann en 1922). Lemaître a ensuite utilisé les données de Slipher pour étayer l'hypothèse selon laquelle l'univers est réellement en expansion et pour estimer le taux d'expansion. Au départ, les scientifiques n'ont accordé que peu d'attention à cet article, peut-être parce que la revue belge n'était pas largement disponible.
Entre-temps, Hubble observait des galaxies à l'aide du télescope de 2,5 mètres situé sur le mont. Wilson, qui était alors le plus grand du monde. Hubble a réalisé les principales observations en collaboration avec un homme remarquable, Milton Humason, qui a abandonné ses études en huitième année et a commencé sa carrière d'astronome en conduisant un train muletier sur le sentier du mont Wilson jusqu'à l'observatoire (Figure\(\PageIndex{2}\)). À ces débuts, les fournitures devaient être acheminées de cette façon ; même les astronomes montaient jusqu'au sommet de la montagne pour leur tour devant le télescope. Humason s'est intéressé au travail des astronomes et, après avoir épousé la fille de l'électricien de l'observatoire, y a pris un emploi de concierge. Après un certain temps, il est devenu assistant de nuit, aidant les astronomes à faire fonctionner le télescope et à enregistrer des données. Finalement, il a fait une telle marque qu'il est devenu astronome à part entière à l'observatoire.

À la fin des années 1920, Humason collaborait avec Hubble en photographiant les spectres de galaxies faibles à l'aide d'un télescope de 2,5 mètres. (À ce moment-là, il ne faisait aucun doute que les nébuleuses spirales étaient en fait des galaxies.) Hubble avait trouvé des moyens d'améliorer la précision des estimations des distances par rapport aux galaxies spirales, et il a pu mesurer des galaxies beaucoup plus faibles et plus éloignées que ce que Slipher pouvait observer avec son télescope beaucoup plus petit. Lorsque Hubble a établi ses propres estimations de distance à côté des mesures des vitesses de récession (la vitesse à laquelle les galaxies s'éloignaient), il a découvert quelque chose d'étonnant : il existait une relation entre la distance et la vitesse pour les galaxies. Plus la galaxie était éloignée, plus elle s'éloignait rapidement de nous.
En 1931, Hubble et Humason ont publié conjointement l'article fondateur dans lequel ils comparaient les distances et les vitesses de galaxies éloignées s'éloignant de nous à des vitesses allant jusqu'à 20 000 kilomètres par seconde et ont pu montrer que les vitesses de récession des galaxies sont directement proportionnelles à leur distance par rapport à nous. (Figure\(\PageIndex{3}\)), comme Lemaître l'avait suggéré.
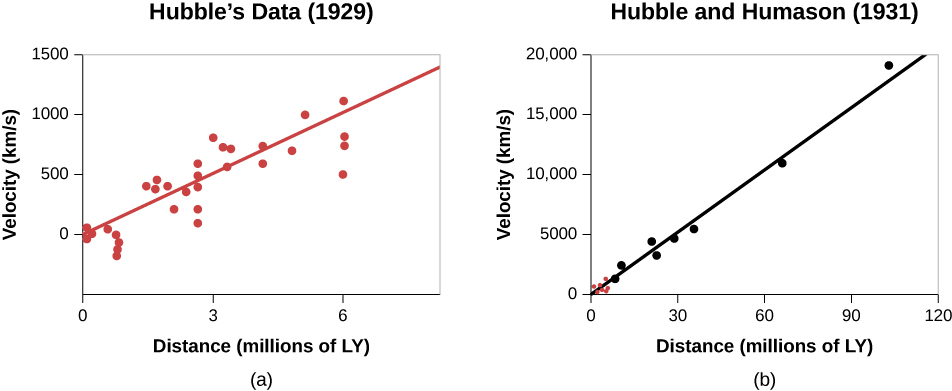
Nous savons maintenant que cette relation vaut pour toutes les galaxies, à l'exception de quelques-unes des plus proches. Presque toutes les galaxies qui s'approchent de nous font partie du groupe de galaxies de la Voie lactée, qui ont leurs propres mouvements, tout comme les oiseaux volant en groupe peuvent voler dans des directions légèrement différentes à des vitesses légèrement différentes, même si l'ensemble du troupeau voyage dans l'espace. ensemble.
Ecrite sous forme de formule, la relation entre la vitesse et la distance est
\[v=H \times d \nonumber\]
où\(v\) est la vitesse de récession,\(d\) est la distance et\(H\) est un nombre appelé constante de Hubble. Cette équation est maintenant connue sous le nom de loi de Hubble.
Constantes de proportionnalité
Les relations mathématiques telles que la loi de Hubble sont assez courantes dans la vie. Pour prendre un exemple simple, supposons que votre collège ou université vous engage pour appeler de riches anciens élèves et leur demander des dons. Vous êtes payé 2,50$ pour chaque appel ; plus vous pouvez passer d'appels entre vos études d'astronomie et d'autres cours, plus vous rapportez d'argent chez vous. Nous pouvons mettre en place une formule qui connecte\(p\), votre paie et\(n\) le nombre d'appels
\[p=A \times n \nonumber\]
où\(A\) est la constante alumni, d'une valeur de 2,50$. Si vous faites 20 appels, vous gagnerez 2,50$ fois 20, soit 50$.
Supposons que votre patron oublie de vous dire combien vous serez payé pour chaque appel. Vous pouvez calculer la constante d'anciens élèves qui régit votre salaire en suivant le nombre d'appels que vous passez et en notant votre salaire brut chaque semaine. Si vous faites 100 appels la première semaine et que vous êtes payé 250$, vous pouvez en déduire que la constante est de 2,50$ (en unités de dollars par appel). Bien entendu, Hubble n'avait aucun « patron » pour lui dire quelle serait sa constante : il devait calculer sa valeur à partir des mesures de distance et de vitesse.
Les astronomes expriment la valeur de la constante de Hubble en unités qui se rapportent à la façon dont ils mesurent la vitesse et la vitesse des galaxies. Dans ce livre, nous utiliserons les kilomètres par seconde et par million d'années-lumière comme unité. Depuis de nombreuses années, les estimations de la valeur de la constante de Hubble se situent entre 15 et 30 kilomètres par seconde et par million d'années-lumière. Les travaux les plus récents semblent converger vers une valeur proche de 22 kilomètres par seconde par million d'années-lumière,\(H\) soit 22 kilomètres par seconde par million de lumière. -années, une galaxie s'éloigne de nous à une vitesse de 22 kilomètres par seconde pour chaque million d'années-lumière de distance. À titre d'exemple, une galaxie située à 100 millions d'années-lumière s'éloigne de nous à une vitesse de 2 200 kilomètres par seconde.
La loi de Hubble nous dit quelque chose de fondamental sur l'univers. Comme toutes les galaxies, à l'exception des plus proches, semblent s'éloigner de nous, les galaxies les plus éloignées se déplaçant le plus rapidement, nous devons vivre dans un univers en expansion. Nous explorerons les implications de cette idée sous peu, ainsi que dans les derniers chapitres de ce texte. Pour l'instant, nous allons simplement dire que l'observation de Hubble sous-tend toutes nos théories sur l'origine et l'évolution de l'univers.
La loi de Hubble et les distances
La régularité exprimée dans la loi de Hubble a un avantage intrinsèque : elle nous donne une nouvelle façon de déterminer les distances par rapport aux galaxies éloignées. Tout d'abord, nous devons établir de manière fiable la constante de Hubble en mesurant à la fois la distance et la vitesse de nombreuses galaxies dans de nombreuses directions afin de nous assurer que la loi de Hubble est vraiment une propriété universelle des galaxies. Mais une fois que nous avons calculé la valeur de cette constante et que nous sommes convaincus qu'elle s'applique partout, une plus grande partie de l'univers s'ouvre à la détermination de la distance. En gros, si nous pouvons obtenir le spectre d'une galaxie, nous pouvons immédiatement déterminer à quelle distance elle se trouve.
La procédure fonctionne de la façon suivante. Nous utilisons le spectre pour mesurer la vitesse à laquelle la galaxie s'éloigne de nous. Si nous mettons ensuite cette vitesse et la constante de Hubble dans l'équation de la loi de Hubble, nous pouvons résoudre la distance.
Exemple\(\PageIndex{1}\) : loi de Hubble
La loi de Hubble (\(v = H \times d\)) nous permet de calculer la distance par rapport à n'importe quelle galaxie. Voici comment nous l'utilisons dans la pratique.
Nous avons mesuré la constante de Hubble à 22 km/s par million d'années-lumière. Cela signifie que si une galaxie se trouve à 1 million d'années-lumière plus loin, elle s'éloignera 22 km/s plus rapidement. Donc, si nous découvrons une galaxie qui s'éloigne à 18 000 km/s, que nous apprend la loi de Hubble sur la distance qui nous sépare de la galaxie ?
Solution
\[d = \frac{v}{H} = \frac{18,000 \text{ km/s}}{ \frac{22 \text{ km/s}}{1 \text{ million light-years}}} = \frac{18,000}{22} \times \frac{1 \text{ million light-years}{1} = 818 \text{ million light-years} \nonumber\]
Remarquez comment nous avons traité les unités ici : le km/s dans le numérateur et le dénominateur s'annulent, et le facteur du million d'années-lumière dans le dénominateur de la constante doivent être divisés correctement avant d'obtenir notre distance de 818 millions d'années-lumière.
Exercice\(\PageIndex{1}\)
En utilisant 22 km/s/millions d'années-lumière pour la constante de Hubble, quelle vitesse de récession attendons-nous de trouver si nous observons une galaxie à 500 millions d'années-lumière ?
- Réponse
-
\[v=d \times H = 500 \text{ million light-years} \times \frac{22 \text{ km/s}}{1 \text{ million light-years}} = 11,000 \text{ km/s} \nonumber\]
Variation de la constante de Hubble
L'utilisation du décalage vers le rouge est potentiellement une technique très importante pour déterminer les distances car, comme nous l'avons vu, la plupart de nos méthodes pour déterminer les distances des galaxies sont limitées aux centaines de millions d'années-lumière les plus proches (et elles comportent de grandes incertitudes à ces distances). L'utilisation de la loi de Hubble comme indicateur de distance ne nécessite que le spectre d'une galaxie et la mesure du décalage Doppler, et avec de grands télescopes et des spectrographes modernes, il est possible de prendre des spectres de galaxies extrêmement faibles.
Mais, comme c'est souvent le cas en science, les choses ne sont pas si simples. Cette technique fonctionne si, et seulement si, la constante de Hubble a été réellement constante tout au long de la vie de l'univers. Lorsque nous observons des galaxies situées à des milliards d'années-lumière, nous les voyons telles qu'elles étaient il y a des milliards d'années. Et si la « constante » de Hubble était différente il y a des milliards d'années ? Avant 1998, les astronomes pensaient que, même si l'univers est en expansion, cette expansion devrait ralentir, voire ralentir, car l'attraction gravitationnelle globale de toute la matière de l'univers aurait un effet dominant et mesurable. Si l'expansion ralentit, la constante de Hubble devrait diminuer au fil du temps.
La découverte que les supernovae de type Ia sont des ampoules standard a donné aux astronomes l'outil dont ils avaient besoin pour observer des galaxies extrêmement éloignées et mesurer leur taux d'expansion il y a des milliards d'années. Les résultats étaient totalement inattendus. Il s'avère que l'expansion de l'univers s'accélère avec le temps ! Ce qui rend ce résultat si étonnant, c'est que les théories physiques existantes ne peuvent en aucun cas expliquer cette observation. Bien que la décélération de l'univers puisse facilement s'expliquer par la gravité, aucune force ou propriété connue des astronomes ne pouvait expliquer cette accélération. Dans le chapitre The Big Bang, nous examinerons plus en détail les observations qui ont conduit à ce résultat totalement inattendu et explorerons ses implications pour le destin ultime de l'univers.
Quoi qu'il en soit, si la constante de Hubble n'est pas vraiment une constante lorsque nous examinons de vastes étendues d'espace et de temps, alors le calcul des distances des galaxies à l'aide de la constante de Hubble ne sera pas précis. Comme nous le verrons dans le chapitre sur le Big Bang, le calcul précis des distances nécessite un modèle de l'évolution de la constante de Hubble au fil du temps. Plus une galaxie est éloignée (et plus nous la voyons depuis longtemps), plus il est important d'inclure les effets du changement de la constante de Hubble. Pour les galaxies situées à quelques milliards d'années-lumière, toutefois, l'hypothèse selon laquelle la constante de Hubble est effectivement constante donne de bonnes estimations de la distance.
Des modèles pour un univers en pleine expansion
Au début, en pensant à la loi de Hubble et en étant fan des œuvres de Copernic et Harlow Shapley, vous pourriez être choqué. Toutes les galaxies s'éloignent-elles vraiment de nous ? Après tout, y a-t-il quelque chose de spécial dans notre position dans l'univers ? Ne vous inquiétez pas ; le fait que les galaxies s'éloignent de nous et que les galaxies les plus éloignées s'éloignent plus rapidement que les galaxies voisines montre simplement que l'univers se développe de manière uniforme.
Un univers en expansion uniforme est un univers qui se développe partout au même rythme. Dans un tel univers, nous et tous les autres observateurs, où qu'ils se trouvent, devons observer une proportionnalité entre les vitesses et les distances de galaxies aussi éloignées. (Ici, nous ignorons le fait que la constante de Hubble n'est pas constante dans le temps, mais si à un moment donné de l'évolution de l'univers la constante de Hubble a la même valeur partout, cet argument fonctionne toujours.)
Pour comprendre pourquoi, imaginez d'abord une règle en caoutchouc extensible, avec les lignes habituelles tracées à chaque centimètre. Supposons maintenant qu'une personne aux bras forts saisisse chaque extrémité de la règle et l'étire lentement de manière à ce que, par exemple, elle double de longueur en 1 minute (Figure\(\PageIndex{4}\)). Imaginez une fourmi intelligente assise sur la marque à 2 centimètres, une pointe qui ne se trouve ni à l'extrémité ni au milieu de la règle. Il mesure la vitesse à laquelle les autres fourmis, assises à 4, 7 et 12 centimètres, s'éloignent de lui lorsque la règle s'étire.

La fourmi à 4 centimètres, à l'origine à 2 centimètres de notre fourmi, a doublé sa distance en 1 minute ; elle s'est donc éloignée à une vitesse de 2 centimètres par minute. La fourmi à 7 centimètres, qui se trouvait à l'origine à 5 centimètres de notre fourmi, est maintenant à 10 centimètres ; elle devait donc se déplacer à 5 centimètres par minute. Celui qui a commencé à 12 centimètres, soit 10 centimètres de la fourmi effectuant le comptage, se trouve maintenant à 20 centimètres, ce qui signifie qu'il a dû s'enfuir à une vitesse de 10 centimètres par minute. À différentes distances, les fourmis s'éloignent à des vitesses différentes, et leur vitesse est proportionnelle à leur distance (comme l'indique la loi de Hubble pour les galaxies). Pourtant, remarquez dans notre exemple que la règle ne faisait que s'étirer de manière uniforme. Remarquez également qu'aucune des fourmis ne se déplaçait d'elle-même, c'est l'étirement de la règle qui les a séparées.
Maintenant, répétons l'analyse, mais plaçons la fourmi intelligente sur une autre marque, disons sur 7 ou 12 centimètres. Nous découvrons que, tant que la règle s'étire uniformément, cette fourmi voit également toutes les autres fourmis s'éloigner à une vitesse proportionnelle à sa distance. En d'autres termes, le type de relation exprimé par la loi de Hubble peut s'expliquer par un étirement uniforme du « monde » des fourmis. Et toutes les fourmis de notre schéma simple verront les autres fourmis s'éloigner d'elles au fur et à mesure que la règle s'étire.
Pour une analogie tridimensionnelle, examinons la miche de pain aux raisins dans la Figure\(\PageIndex{5}\). La chef a accidentellement mis trop de levure dans la pâte, et lorsqu'elle fait lever le pain, il double de volume au cours de l'heure suivante, ce qui fait que tous les raisins secs s'éloignent davantage. Sur la figure, nous choisissons à nouveau un raisin représentatif (qui ne se trouve ni au bord ni au centre du pain) et indiquons les distances entre celui-ci et plusieurs autres sur la figure (avant et après l'expansion du pain).
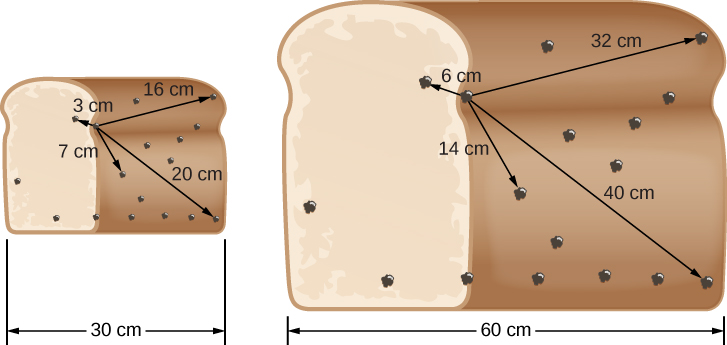
Mesurez l'augmentation de la distance et calculez vous-même les vitesses sur le pain aux raisins, comme nous l'avons fait pour la règle. Vous verrez que, puisque chaque distance double au cours de l'heure, chaque raisin s'éloigne du raisin sélectionné à une vitesse proportionnelle à sa distance. Il en va de même quel que soit le raisin avec lequel vous commencez.
Nos deux analogies sont utiles pour clarifier notre pensée, mais il ne faut pas les prendre au pied de la lettre. Sur la règle et sur le pain aux raisins secs, il y a des pointes au bout ou sur le bord. Vous pouvez les utiliser pour localiser le milieu de la règle et du pain. Bien que nos modèles de l'univers ressemblent quelque peu aux propriétés de la règle et du pain, l'univers n'a ni frontières, ni bords, ni centre (autant d'idées ahurissantes que nous aborderons dans un chapitre ultérieur).
Ce qu'il est utile de noter à propos des fourmis et des raisins secs, c'est qu'ils n'ont pas eux-mêmes « provoqué » leur mouvement. Ce n'est pas comme si les raisins avaient décidé de faire un voyage loin l'un de l'autre et avaient ensuite sauté sur un hoverboard pour s'évader. Non, dans nos deux analogies, c'est l'étirement du médium (la règle ou le pain) qui a éloigné les fourmis ou les raisins secs. De la même manière, nous verrons dans le chapitre The Big Bang que les galaxies ne sont pas équipées de moteurs-fusées qui les propulsent les unes des autres. Ils participent plutôt de manière passive à l'expansion de l'espace. À mesure que l'espace s'étend, les galaxies s'éloignent de plus en plus les unes des autres, tout comme l'étaient les fourmis et les raisins secs. (Si cette notion d' « étirement » de l'espace vous surprend ou vous dérange, c'est le bon moment pour passer en revue les informations sur l'espace-temps dans les trous noirs et l'espace-temps incurvé. Nous discuterons de ces idées plus en détail au fur et à mesure que notre discussion s'étendra des galaxies à l'univers entier.)
D'ailleurs, l'expansion de l'univers ne signifie pas que les galaxies individuelles et les amas de galaxies eux-mêmes sont en expansion. Dans notre analogie, ni les raisins secs ni les fourmis ne grossissent à mesure que le pain se dilate. De même, la gravité maintient les galaxies et les amas de galaxies ensemble, et ils s'éloignent les uns des autres, sans changer eux-mêmes de taille, à mesure que l'univers s'étend.
Résumé
L'univers est en pleine expansion. Les observations montrent que les raies spectrales des galaxies lointaines sont décalées vers le rouge et que leur vitesse de récession est proportionnelle à leur distance par rapport à nous, une relation connue sous le nom de loi de Hubble. Le taux de récession, appelé constante de Hubble, est d'environ 22 kilomètres par seconde et par million d'années-lumière. Nous ne sommes pas au centre de cette expansion : un observateur de n'importe quelle autre galaxie verrait le même schéma d'expansion que nous. L'expansion décrite par la loi de Hubble est mieux comprise comme un étirement de l'espace.
Lexique
- Constante de Hubble
- une constante de proportionnalité dans la loi liant les vitesses des galaxies éloignées à leurs distances
- Loi de Hubble
- une règle selon laquelle les vitesses radiales des galaxies éloignées sont proportionnelles à leur distance par rapport à nous
- redshift
- lorsque les raies du spectre sont déplacées vers des longueurs d'onde plus longues (vers l'extrémité rouge du spectre visible)


