19.2 : Surveiller les étoiles

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Comprendre le concept de triangulation des distances par rapport à des objets distants, y compris les étoiles
• Expliquer pourquoi les satellites basés dans l'espace fournissent des distances plus précises que les méthodes terrestres
• Discutez des efforts déployés par les astronomes pour étudier les étoiles les plus proches du Soleil

Passer des planètes aux étoiles est un pas énorme. Par exemple, notre sonde Voyager 1, qui a été lancée en 1977, a maintenant voyagé plus loin de la Terre que tout autre vaisseau spatial. Comme il est écrit en 2016, Voyager 1 se trouve à 134 UA du Soleil. ¹ L'étoile la plus proche se trouve toutefois à des centaines de milliers d'UA de la Terre. Malgré cela, nous pouvons, en principe, mesurer les distances par rapport aux étoiles en utilisant la même technique qu'un ingénieur civil utilise pour étudier la distance jusqu'à une montagne ou un arbre inaccessible : la méthode de triangulation.

Triangulation dans l'espace

Un exemple pratique de triangulation est votre propre perception de la profondeur. Comme vous êtes heureux de le découvrir chaque matin lorsque vous vous regardez dans le miroir, vos deux yeux sont situés à une certaine distance l'un de l'autre. Vous visualisez donc le monde depuis deux points de vue différents, et c'est cette double perspective qui vous permet d'avoir une idée générale de la distance entre les objets.

Pour comprendre ce que nous voulons dire, prenez un stylo et tenez-le quelques centimètres devant votre visage. Regardez-le d'abord avec un œil (en fermant l'autre), puis changez d'œil. Remarquez comment le stylo semble se déplacer par rapport aux objets de la pièce. Tenez maintenant le stylo à bout de bras : le décalage est moindre. Si vous jouez avec le stylet pendant un moment, vous remarquerez que plus vous le tenez loin, moins il semble bouger. Votre cerveau effectue automatiquement de telles comparaisons et vous donne une assez bonne idée de la distance qui se trouve dans votre voisinage immédiat.

Si vos bras étaient en caoutchouc, vous pourriez étirer le stylo suffisamment loin de vos yeux pour que le décalage devienne imperceptible. Cela est dû au fait que notre perception de la profondeur échoue pour les objets situés à plus de quelques dizaines de mètres. Pour voir le déplacement d'un objet situé à un pâté de maisons ou plus de vous, il faudrait que vos yeux soient bien plus éloignés.

Voyons comment les géomètres tirent parti de la même idée. Supposons que vous essayiez de mesurer la distance entre un arbre et une rivière profonde (Figure\(\PageIndex{1}\)). Vous avez installé deux stations d'observation à une certaine distance. Cette distance (ligne AB sur la figure\(\PageIndex{1}\)) est appelée ligne de base. La direction vers l'arbre (C sur la figure) par rapport à la ligne de base est maintenant observée à partir de chaque station. Notez que C apparaît dans des directions différentes depuis les deux stations. Ce changement apparent de direction de l'objet distant dû à un changement du point de vue de l'observateur est appelé parallaxe.

\(\PageIndex{1}\)Triangulation de figures. La triangulation permet de mesurer les distances par rapport à des objets inaccessibles. En obtenant l'angle par rapport à un arbre depuis deux points de vue différents, nous pouvons calculer les propriétés du triangle qu'ils forment et donc la distance par rapport à l'arbre.

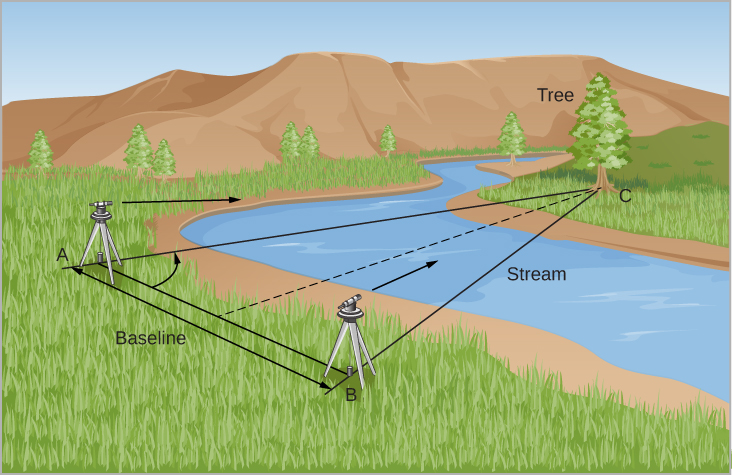
La parallaxe est également l'angle que forment les lignes AC et BC, en termes mathématiques, l'angle sous-tendu par la ligne de base. La connaissance des angles en A et B et de la longueur de la ligne de base, AB, permet de résoudre le triangle ABC pour n'importe laquelle de ses dimensions, par exemple la distance AC ou BC. La solution pourrait être atteinte en construisant un dessin à l'échelle ou en utilisant la trigonométrie pour effectuer un calcul numérique. Si l'arbre était plus éloigné, le triangle entier serait plus long et plus fin, et l'angle de parallaxe serait plus petit. Ainsi, nous avons la règle générale selon laquelle plus la parallaxe est petite, plus l'objet que nous mesurons doit être éloigné.

Dans la pratique, les types de lignes de base que les géomètres utilisent pour mesurer les distances sur Terre sont totalement inutiles lorsque nous essayons de mesurer des distances dans l'espace. Plus un objet astronomique est éloigné, plus la ligne de base doit être longue pour nous donner une chance raisonnable d'effectuer une mesure. Malheureusement, presque tous les objets astronomiques sont très éloignés. Pour mesurer leurs distances, il faut disposer d'une base de référence très large et de mesures angulaires très précises. La Lune est le seul objet suffisamment proche pour que sa distance puisse être trouvée assez précisément à l'aide de mesures effectuées sans télescope. Ptolémée a déterminé correctement la distance par rapport à la Lune à quelques pour cent près. Il a utilisé la Terre tournante elle-même comme base de référence, mesurant la position de la Lune par rapport aux étoiles à deux heures différentes de la nuit.

À l'aide de télescopes, les astronomes ont ensuite pu mesurer les distances par rapport aux planètes et aux astéroïdes les plus proches en utilisant le diamètre de la Terre comme base de référence. C'est ainsi que l'UA a été créée pour la première fois. Pour atteindre les étoiles, il faut toutefois disposer d'une base de référence beaucoup plus longue pour la triangulation et des mesures extrêmement sensibles. Une telle base de référence est fournie par le voyage annuel de la Terre autour du Soleil.

Distances des étoiles

Lorsque la Terre se déplace d'un côté à l'autre de son orbite, elle nous fournit gracieusement une base de référence de 2 UA, soit environ 300 millions de kilomètres. Bien qu'il s'agisse d'une ligne de référence beaucoup plus grande que le diamètre de la Terre, les étoiles sont si éloignées que le décalage de parallaxe qui en résulte n'est toujours pas visible à l'œil nu, même pour les étoiles les plus proches.

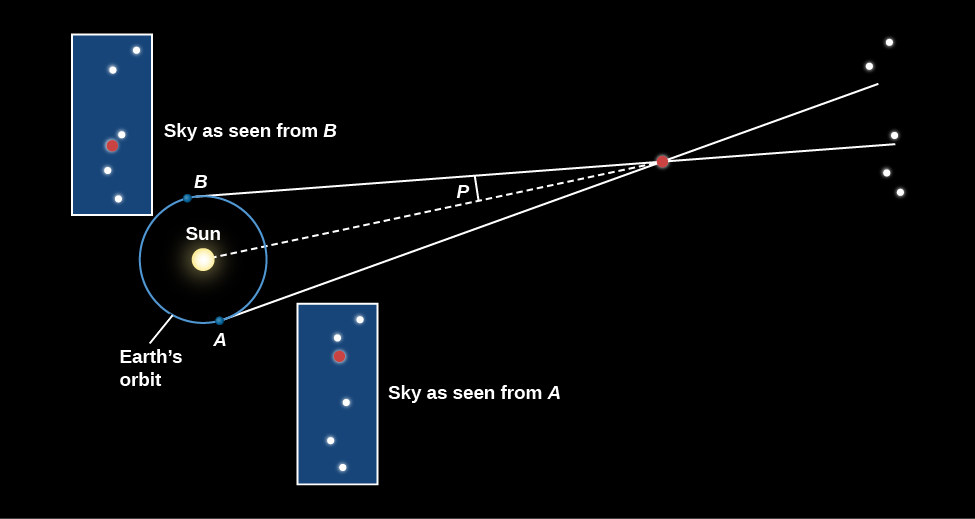
Dans le chapitre intitulé Observing the Sky : The Birth of Astronomy, nous avons expliqué comment ce dilemme laissait perplexe chez les Grecs de l'Antiquité, dont certains avaient même suggéré que le Soleil pourrait être le centre du système solaire, avec la Terre en mouvement autour de lui. Aristote et d'autres ont toutefois fait valoir que la Terre ne pouvait pas tourner autour du Soleil. Selon eux, si c'était le cas, nous observerions sûrement la parallaxe des étoiles les plus proches sur fond d'objets plus éloignés lorsque nous observons le ciel depuis différentes parties de l'orbite de la Terre (Figure\(\PageIndex{3}\)). Tycho Brahe (1546—1601) a avancé le même argument erroné près de 2000 ans plus tard, lorsque ses mesures minutieuses de la position des étoiles à l'œil nu n'ont révélé aucun changement de ce type.

Ces premiers observateurs ne se rendaient pas compte de la distance réelle entre les étoiles et de l'importance du changement de leur position, même avec l'ensemble de l'orbite de la Terre comme base de référence. Le problème était qu'ils ne disposaient pas d'outils pour mesurer les décalages de parallaxe trop faibles pour être observés à l'œil nu. Au XVIIIe siècle, lorsqu'il n'y avait plus de doute sérieux quant à la révolution de la Terre, il est devenu évident que les étoiles devaient être extrêmement éloignées. Les astronomes équipés de télescopes ont commencé à concevoir des instruments capables de mesurer les petits déplacements des étoiles voisines par rapport à l'arrière-plan d'objets célestes plus éloignés (et donc immuables).

Cela représentait un défi technique important, car, même pour les étoiles les plus proches, les angles de parallaxe ne représentent généralement qu'une fraction de seconde d'arc. Rappelez-vous qu'une seconde d'arc (arcsec) est un angle de seulement 1/3600 de degré. Une pièce de la taille d'un quart américain semblerait avoir un diamètre de 1 seconde d'arc si vous l'observez à une distance d'environ 5 kilomètres (3 miles). Pensez à quel point cet angle est petit. Il n'est donc pas étonnant qu'il ait fallu beaucoup de temps aux astronomes avant de pouvoir mesurer de si petits déplacements.

Les premières détections réussies de parallaxe stellaire ont eu lieu en 1838, lorsque Friedrich Bessel en Allemagne (Figure\(\PageIndex{2}\)), Thomas Henderson, un astronome écossais travaillant au Cap de Bonne-Espérance, et Friedrich Struve en Russie ont mesuré indépendamment les parallaxes des étoiles 61 Cygni, Alpha Centauri, et Vega, respectivement. Même l'étoile la plus proche, Alpha Centauri, a montré un déplacement total d'environ 1,5 seconde d'arc au cours d'une année seulement.

Figure\(\PageIndex{2}\) Friedrich Wilhelm Bessel (1784-1846), Thomas J. Henderson (1798-1844) et Friedrich Struve (1793-1864). (a) Bessel a effectué la première mesure authentifiée de la distance par rapport à une étoile (61 cygnes) en 1838, un exploit qui avait échappé à de nombreux astronomes dévoués pendant près d'un siècle. Mais deux autres, (b) l'astronome écossais Thomas J. Henderson et (c) Friedrich Struve, en Russie, l'ont suivi de près.

La figure\(\PageIndex{3}\) montre comment ces mesures fonctionnent. Vue de part et d'autre de l'orbite de la Terre, une étoile proche change de position par rapport à une configuration d'étoiles plus éloignées. Les astronomes définissent en fait la parallaxe comme étant la moitié de l'angle qu'une étoile se déplace lorsqu'elle est vue de part et d'autre de l'orbite de la Terre (angle marqué P sur la figure\(\PageIndex{3}\)). La raison de cette définition est simplement qu'ils préfèrent traiter avec une base de référence de 1 UA au lieu de 2 UA.

Figure\(\PageIndex{3}\) Parallax., Alors que la Terre tourne autour du Soleil, la direction dans laquelle nous voyons une étoile proche varie par rapport aux étoiles éloignées. Nous définissons la parallaxe de l'étoile la plus proche comme étant la moitié du changement total de direction, et nous la mesurons généralement en secondes d'arc.

Unités de distance stellaire

Avec une base de référence d'une UA, à quelle distance devrait-elle se trouver une étoile pour avoir une parallaxe de 1 seconde d'arc ? La réponse s'avère être 206 265 UA, soit 3,26 années-lumière. Cela équivaut à 3,1 × 10 ¹³ kilomètres (en d'autres termes, 31 billions de kilomètres). Nous donnons à cette unité un nom spécial, le parsec (pc), dérivé de « la distance à laquelle nous avons un par allax d'une seconde ». La distance (\(D\)) d'une étoile en parsecs est juste l'inverse de sa parallaxe (p) en secondes d'arc, c'est-à-dire

\[D=\frac{1}{p} \nonumber\]

Ainsi, une étoile ayant une parallaxe de 0,1 seconde d'arc serait trouvée à une distance de 10 parsecs, et une étoile ayant une parallaxe de 0,05 seconde d'arc se trouverait à 20 parsecs.

À l'époque où la plupart de nos distances provenaient de mesures de parallaxe, le parsec était une unité de distance utile, mais il n'est pas aussi intuitif que l'année-lumière. L'un des avantages de l'année-lumière en tant qu'unité est qu'elle met l'accent sur le fait que, lorsque nous regardons dans l'espace, nous regardons également dans le temps. La lumière que nous voyons d'une étoile située à 100 années-lumière a quitté cette étoile il y a 100 ans. Ce que nous étudions n'est pas l'étoile telle qu'elle est aujourd'hui, mais plutôt telle qu'elle était dans le passé. La lumière qui atteint nos télescopes aujourd'hui à partir de galaxies lointaines les a quittés avant même que la Terre n'existe.

Dans ce texte, nous utiliserons les années-lumière comme unité de distance, mais de nombreux astronomes utilisent encore des parsecs lorsqu'ils rédigent des articles techniques ou discutent entre eux lors de réunions. Pour effectuer une conversion entre les deux unités de distance, il suffit de garder à l'esprit que 1 parsec = 3,26 année-lumière et 1 année-lumière = 0,31 parsec.

Exemple\(\PageIndex{1}\) : À quelle distance se trouve une année-lumière ?

Une année-lumière est la distance parcourue par la lumière en 1 an. Étant donné que la lumière se déplace à une vitesse de 300 000 km/s, combien de kilomètres y a-t-il par année-lumière ?

Solution

Nous avons appris plus tôt que vitesse = distance/temps. Nous pouvons réorganiser cette équation de telle sorte que\(\text{distance } = \text{ velocity } \times \text{ time }\). Maintenant, nous devons déterminer le nombre de secondes par an.

Il y a environ 365 jours par an. Pour déterminer le nombre de secondes, il faut estimer le nombre de secondes par jour.

Nous pouvons changer les unités comme suit (remarquez comment les unités de temps s'annulent) :

\[ 1 \text{ day } \times 24 \text{ hr/day } \times 60 \text{ min/hr } \times 60 \text{ s/min } = 86,400 \text{ s/day} \nonumber\]

Ensuite, pour obtenir le nombre de secondes par an :

\[ 365 \text{ days/year } \times 86,400 \text{ s/day } = 31,536,000 \text{ s/year} \nonumber\]

Nous pouvons maintenant multiplier la vitesse de la lumière par le nombre de secondes par an pour obtenir la distance parcourue par la lumière en 1 an :

\[ \begin{aligned} \text{distance } & = \text{ velocity } \times \text{ time} \\ & = 300,000 \text{ km/s } \times 31,536,000 \text{ s} \\ & =9.46 \times 10^{12} \text{ km} \end{aligned} \nonumber\]

Cela représente près de 10 000 000 000 000 km que la lumière parcourt en un an. Pour vous aider à imaginer la longueur de cette distance, mentionnons qu'une ficelle d'une année-lumière pourrait faire 236 millions de fois le tour de la Terre.

Exercice\(\PageIndex{1}\)

Le chiffre ci-dessus est vraiment important. Que se passerait-il si nous le définissions dans des termes qui seraient un peu plus compréhensibles, comme le diamètre de la Terre ? Le diamètre de la Terre est d'environ 12 700 km.

Réponse

\[ \begin{aligned} 1 \text{ light-year } & = 9.46 \times 10^{12} \text{ km} \\ & =9.46 \times 10^{12} \text{ km } \times \frac{1 \text{ Earth diameter}}{12,700 \text{ km}} \\ & =7.45 \times 10^8 \text{ Earth diameters} \end{aligned} \nonumber\]

Cela signifie qu'une année-lumière représente environ 745 millions de fois le diamètre de la Terre.

NOMMER DES ÉTOILES

Vous vous demandez peut-être pourquoi les étoiles ont un assortiment de noms si confus. Il suffit de regarder les trois premières étoiles pour mesurer leurs parallaxes : 61 Cygni, Alpha Centauri et Vega. Chacun de ces noms est issu d'une tradition différente de désignation des étoiles.

Les étoiles les plus brillantes portent des noms qui proviennent des anciens. Certains viennent du grec, comme Sirius, qui signifie « celui qui a été brûlé », en référence à son éclat. Quelques-uns viennent du latin, mais la plupart des noms les plus connus viennent de l'arabe car, comme indiqué dans Observing the Sky : The Birth of Astronomy, une grande partie de l'astronomie grecque et romaine a été « redécouverte » en Europe après l'âge des ténèbres au moyen de traductions arabes. Vega, par exemple, signifie « aigle plongeant » et Bételgeuse (prononcé « jus de scarabée ») signifie « main droite de la main centrale ».

En 1603, l'astronome allemand Johann Bayer (1572-1625) a introduit une approche plus systématique pour nommer les étoiles. Pour chaque constellation, il a attribué une lettre grecque aux étoiles les plus brillantes, approximativement par ordre de luminosité. Dans la constellation d'Orion, par exemple, Bételgeuse est l'étoile la plus brillante. Elle a donc reçu la première lettre de l'alphabet grec, alpha, et est connue sous le nom d'Alpha Orionis. (« Orionis » est la forme possessive d'Orion, donc Alpha Orionis signifie « le premier d'Orion ».) Une étoile appelée Rigel, la deuxième plus brillante de cette constellation, s'appelle Beta Orionis (Figure\(\PageIndex{4}\)). Comme il y a 24 lettres dans l'alphabet grec, ce système permet d'étiqueter 24 étoiles dans chaque constellation, mais les constellations ont beaucoup plus d'étoiles que cela.

\(\PageIndex{4}\)Figurines des objets dans Orion. (a) Cette image montre les objets les plus brillants dans ou à proximité du motif étoilé d'Orion, le chasseur (de la mythologie grecque), dans la constellation d'Orion. (b) Notez les lettres grecques du système de Bayer dans ce schéma de la constellation d'Orion. Les objets désignés M42, M43 et M78 ne sont pas des étoiles mais des nébuleuses, des nuages de gaz et de poussière ; ces chiffres proviennent d'une liste d' « objets flous » dressée par Charles Messier en 1781.

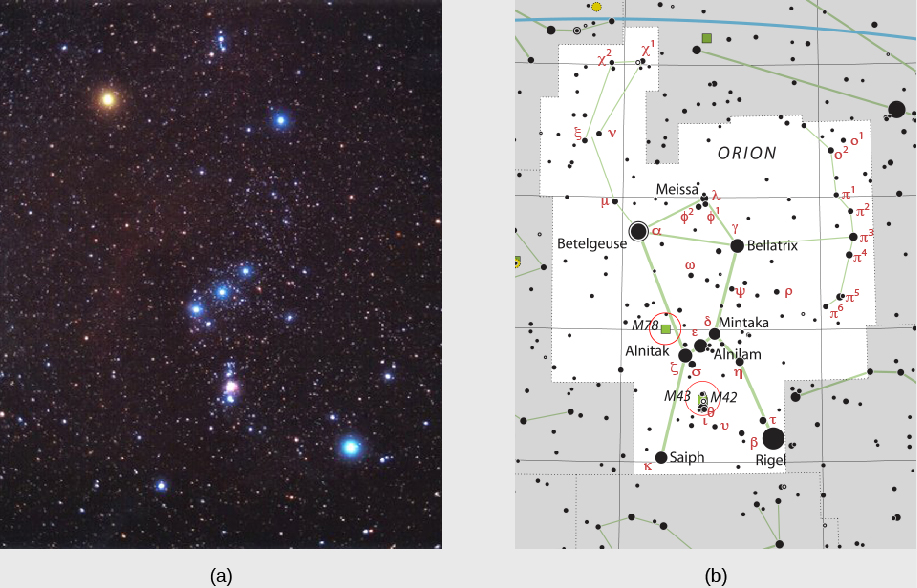
En 1725, l'astronome anglais Royal John Flamsteed a introduit un autre système, dans lequel les étoiles les plus brillantes ont finalement obtenu un numéro dans chaque constellation en fonction de leur position dans le ciel ou, plus précisément, de leur ascension droite. (Le système de coordonnées du ciel qui inclut l'ascension vers la droite a été discuté dans Terre, Lune et Ciel.) Dans ce système, Bételgeuse est appelée 58 Orionis et 61 Cygni est la 61e étoile de la constellation du Cygne, le cygne.

Ça ne fait qu'empirer. Au fur et à mesure que les astronomes ont commencé à mieux comprendre les étoiles, ils ont élaboré une série de catalogues d'étoiles spécialisés, et les fans de ces catalogues ont commencé à appeler les étoiles par leur numéro de catalogue. Si vous regardez l'annexe I, notre liste des étoiles les plus proches (dont beaucoup sont beaucoup trop faibles pour obtenir un nom ancien, une lettre de Bayer ou un numéro Flamsteed), vous verrez des références à certains de ces catalogues. Un exemple est un ensemble d'étoiles étiquetées avec un numéro BD, pour « Bonner Durchmusterung ». Il s'agissait d'un catalogue gigantesque de plus de 324 000 étoiles réparties dans une série de zones du ciel, organisé à l'Observatoire de Bonn dans les années 1850 et 1860. N'oubliez pas que ce catalogue a été créé avant que la photographie ou les ordinateurs ne soient utilisés, de sorte que la position de chaque étoile devait être mesurée (au moins deux fois) à l'œil nu, ce qui était une entreprise ardue.

Il existe également un système complètement différent pour suivre les étoiles dont la luminosité varie, et un autre pour les étoiles qui brillent de manière explosive à des moments imprévisibles. Les astronomes se sont habitués aux nombreux systèmes de dénomination des étoiles, mais les étudiants les trouvent souvent déconcertants et souhaitent que les astronomes choisissent l'un d'entre eux. Ne retenez pas votre souffle : en astronomie, comme dans de nombreux domaines de la pensée humaine, la tradition a un puissant attrait. Néanmoins, avec des bases de données informatiques à haute vitesse pour améliorer la mémoire humaine, les noms peuvent devenir de moins en moins nécessaires. Les astronomes d'aujourd'hui désignent souvent les étoiles par leur position précise dans le ciel plutôt que par leur nom ou divers numéros de catalogue.

Les étoiles les plus proches

Aucune étoile connue (autre que le Soleil) ne se trouve à moins d'une année-lumière ou même d'un parsec de la Terre. Les étoiles voisines les plus proches du Soleil sont trois étoiles de la constellation du Centaure. À l'œil nu, la plus brillante de ces trois étoiles est Alpha Centauri, qui se trouve à seulement 30○ du pôle sud céleste et n'est donc pas visible depuis la partie continentale des États-Unis. Alpha Centauri lui-même est une étoile binaire, deux étoiles en révolution mutuelle, trop proches l'une de l'autre pour être distinguée sans télescope. Ces deux étoiles se trouvent à 4,4 années-lumière de nous. À proximité se trouve une troisième étoile faible, connue sous le nom de Proxima Centauri. Proxima, à une distance de 4,3 années-lumière, est légèrement plus proche de nous que les deux autres étoiles. Si Proxima Centauri fait partie d'un système d'étoiles triple avec le binaire Alpha Centauri, comme cela semble probable, alors sa période orbitale pourrait être supérieure à 500 000 ans.

Proxima Centauri est un exemple du type d'étoile le plus courant et de notre voisin stellaire le plus courant (comme nous l'avons vu dans Stars : A Celestial Census). Les naines M rouges de faible masse constituent environ 70 % de toutes les étoiles et dominent le recensement des étoiles situées à moins de 10 parsecs du Soleil. La dernière étude du voisinage solaire a dénombré 357 étoiles et naines brunes dans un rayon de 10 parsecs, dont 248 sont des naines rouges. Pourtant, si vous vouliez voir un nain M à l'œil nu, vous n'auriez pas de chance. Ces étoiles ne produisent qu'une fraction de la lumière du Soleil, et presque toutes nécessitent un télescope pour être détectées.

L'étoile la plus proche visible sans télescope depuis la majeure partie des États-Unis est l'étoile la plus brillante de toutes, Sirius, qui a une distance d'un peu plus de 8 années-lumière. Il s'agit également d'un système binaire, composé d'une faible naine blanche orbitant autour d'une étoile bleu-blanc de la séquence principale. C'est une coïncidence de chiffres intéressante que la lumière nous parvient du Soleil en 8 minutes environ et de la prochaine étoile la plus brillante du ciel en 8 ans environ.

Exemple\(\PageIndex{2}\) : calcul du diamètre du soleil

Pour les étoiles voisines, nous pouvons mesurer le changement apparent de leur position lorsque la Terre tourne autour du Soleil. Nous avons écrit plus tôt qu'un objet doit être distant de 206 265 UA pour avoir une parallaxe d'une seconde d'arc. Cela peut sembler un nombre très étrange, mais vous pouvez comprendre pourquoi il s'agit de la bonne valeur. Nous allons commencer par estimer le diamètre du Soleil, puis appliquer la même idée à une étoile dont la parallaxe est de 1 seconde d'arc. Faites un croquis avec un cercle rond pour représenter le Soleil, placez la Terre à une certaine distance et placez un observateur dessus. Tracez deux lignes à partir du point où se trouve l'observateur, une de chaque côté du Soleil. Dessinez un cercle centré sur la Terre et dont la circonférence passe par le centre du Soleil. Maintenant, pensez aux proportions. Le Soleil s'étend sur environ un demi-degré dans le ciel. Un cercle complet contient 360○. La circonférence du cercle centré sur la Terre et passant par le Soleil est donnée par :

\[\text{circumference } =2 \pi \times 93,000,000 \text{ miles} \nonumber\]

Les deux ratios suivants sont alors égaux :

\[\frac{0.5^{\circ}}{360^{\circ}} = \frac{\text{diameter of Sun}}{2 \pi \times 93,000,000} \nonumber\]

Calculez le diamètre du soleil. Comment votre réponse se compare-t-elle au diamètre réel ?

Solution

Pour déterminer le diamètre du Soleil, nous pouvons évaluer l'expression ci-dessus.

\ [\ begin {aligné} \ text {diamètre du soleil} & = \ frac {0.5^ {\ circ}} {360^ {\ circ}}
 \ times 2 \ pi \ times 93 000 000 \ text {miles} \ \ =811 577 \ text {miles} \ end {aligné} \ nonnumber \]

C'est très proche de la valeur réelle d'environ 848 000 miles.

Exercice\(\PageIndex{2}\)

Appliquez maintenant cette idée au calcul de la distance par rapport à une étoile dont la parallaxe est de 1 seconde d'arc. Dessinez une image similaire à celle que nous avons suggérée ci-dessus et calculez la distance en UA. (Conseil : n'oubliez pas que l'angle de parallaxe est défini par 1 UA, et non par 2 UA, et que 3 600 secondes d'arc = 1 degré.)

Réponse

206 265 AU

Mesurer les parallaxes dans l'espace

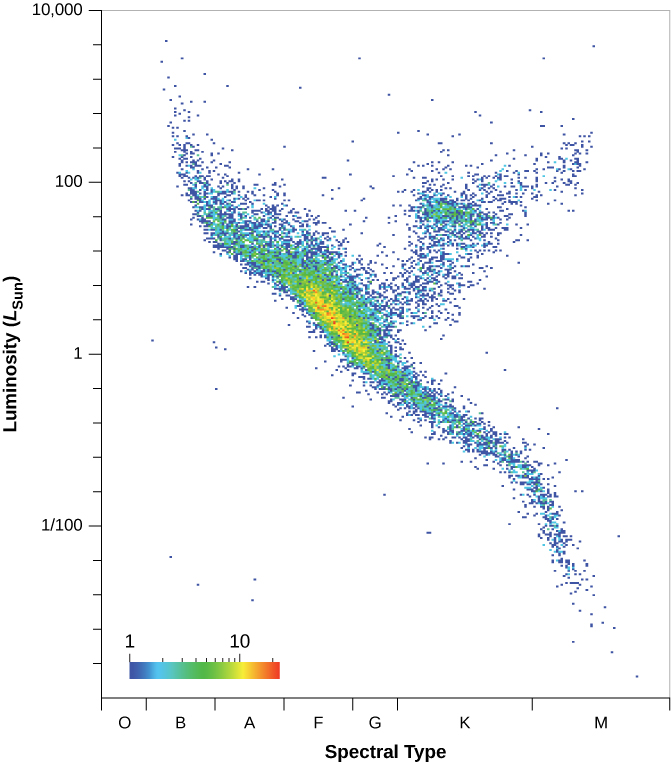
Les mesures de la parallaxe stellaire ont été révolutionnées par le lancement de l'engin spatial Hipparcos en 1989, qui a mesuré les distances de milliers d'étoiles sur environ 300 années-lumière avec une précision de 10 à 20 % (voir la figure\(\PageIndex{5}\) et le reportage sur la parallaxe et l'astronomie spatiale ci-dessous). Cependant, même 300 années-lumière représentent moins de 1 % de la taille du disque principal de notre Galaxie.

En décembre 2013, le successeur d'Hipparcos, nommé Gaia, a été lancé par l'Agence spatiale européenne. Gaia mesure la position et les distances par rapport à près d'un milliard d'étoiles avec une précision de quelques millionièmes de seconde d'arc. La limite de distance de Gaia s'étendra bien au-delà d'Hipparcos et étudiera les étoiles jusqu'à 30 000 années-lumière (100 fois plus loin qu'Hipparcos, couvrant près du tiers du disque galactique). Gaia sera également capable de mesurer les mouvements appropriés ² pour des milliers d'étoiles dans le halo de la Voie lactée, ce qui n'est possible que pour les étoiles les plus brillantes à l'heure actuelle. À la fin de la mission de Gaia, nous disposerons non seulement d'une carte tridimensionnelle d'une grande partie de notre propre galaxie de la Voie lactée, mais nous aurons également un maillon fort dans la chaîne de distances cosmiques dont nous parlons dans ce chapitre. Pourtant, pour étendre cette chaîne au-delà de la portée de Gaia et explorer les distances jusqu'aux galaxies voisines, nous avons besoin de techniques complètement nouvelles.

Figure\(\PageIndex{5}\) H—R Diagramme des étoiles mesurées par Gaia et Hipparcos. Ce graphique comprend 16 631 étoiles pour lesquelles les parallaxes ont une précision de 10 % ou mieux. Les couleurs indiquent le nombre d'étoiles à chaque point du diagramme, le rouge correspondant au plus grand nombre et le bleu au plus petit. La luminosité est tracée le long de l'axe vertical, la luminosité augmentant vers le haut. Une couleur infrarouge est tracée comme indicateur de la température, la température diminuant vers la droite. La plupart des points de données sont répartis le long de la diagonale allant du coin supérieur gauche (haute luminosité, haute température) au coin inférieur droit (basse température, faible luminosité). Ce sont les étoiles de la séquence principale. La grande masse de points de données située au-dessus de la séquence principale sur le côté droit du diagramme est composée d'étoiles géantes rouges.

parallaxe et astronomie spatiale

L'un des aspects les plus difficiles de la mesure précise des petits angles de déplacement de parallaxe par rapport à la Terre est d'observer les étoiles à travers l'atmosphère de notre planète. Comme nous l'avons vu dans Astronomical Instruments, l'atmosphère a pour effet de répartir les points de lumière des étoiles en disques flous, ce qui rend plus difficile la mesure exacte de leur position. Les astronomes rêvaient depuis longtemps de pouvoir mesurer des parallaxes depuis l'espace, et deux observatoires orbitaux ont aujourd'hui concrétisé ce rêve.

Le nom du satellite Hipparcos, lancé en 1989 par l'Agence spatiale européenne, est à la fois l'abréviation de High Precision Parallax Collecting Satellite et un hommage à Hipparque, l'astronome grec pionnier dont nous avons discuté dans Observing the Sky : The Birth of Astronomy. Le satellite a été conçu pour effectuer les mesures de parallaxe les plus précises de l'histoire, à 36 000 kilomètres au-dessus de la Terre. Cependant, son moteur-fusée embarqué n'a pas tiré, ce qui signifie qu'il n'a pas reçu le coup de pouce nécessaire pour atteindre l'altitude souhaitée. Hipparcos a fini par passer sa vie de 4 ans sur une orbite elliptique à une altitude comprise entre 500 et 36 000 kilomètres. Sur cette orbite, le satellite a plongé dans les ceintures de rayonnement de la Terre toutes les 5 heures environ, ce qui a finalement fait des ravages sur les panneaux solaires qui fournissaient l'énergie nécessaire à l'alimentation des instruments.

Néanmoins, la mission a été couronnée de succès et a donné lieu à deux catalogues. L'une indique la position de 120 000 étoiles avec une précision d'un millième de seconde d'arc, soit environ le diamètre d'une balle de golf à New York vue depuis l'Europe. Le deuxième catalogue contient des informations sur plus d'un million d'étoiles, dont les positions ont été mesurées à trente millièmes de seconde d'arc. Nous avons maintenant des mesures de parallaxe précises des étoiles à des distances d'environ 300 années-lumière. (Avec les télescopes au sol, des mesures précises n'étaient possibles que sur une soixantaine d'années-lumière.)

Afin de tirer parti du succès d'Hipparcos, l'Agence spatiale européenne a lancé en 2013 un nouveau satellite appelé Gaia. La mission Gaia devrait durer 5 ans. Comme Gaia possède des télescopes plus grands que Hipparcos, elle peut observer des étoiles plus pâles et mesurer leur position 200 fois plus précisément. L'objectif principal de la mission Gaia est de dresser une carte tridimensionnelle précise de cette partie de la Galaxie dans un rayon d'environ 30 000 années-lumière en observant un milliard d'étoiles 70 fois chacune, en mesurant leur position et donc leurs parallaxes ainsi que leur luminosité.

Pendant longtemps, la mesure des parallaxes et de la position précise des étoiles a été un échec de la recherche astronomique, principalement parce que la précision des mesures ne s'est pas beaucoup améliorée pendant environ 100 ans. Cependant, la capacité d'effectuer des mesures depuis l'espace a révolutionné ce domaine de l'astronomie et continuera de constituer un maillon essentiel de notre chaîne de distances cosmiques.

L'Agence spatiale européenne (ESA) gère un site Web de la mission Gaia sur lequel vous pouvez en savoir plus sur la mission Gaia et obtenir les dernières nouvelles sur les observations de Gaia.

Pour en savoir plus sur Hipparcos, explorez cette page Web de l'Agence spatiale européenne avec un podcast de l'ESA cartographiant la galaxie, d'Hipparcos à Gaia.

Résumé

Pour les étoiles relativement proches, nous pouvons « trianguler » les distances à partir d'une ligne de base créée par le mouvement annuel de la Terre autour du Soleil. La moitié du décalage de la position d'une étoile proche par rapport à des étoiles de fond très éloignées, observée de part et d'autre de l'orbite de la Terre, est appelée parallaxe de cette étoile et constitue une mesure de sa distance. Les unités utilisées pour mesurer la distance stellaire sont l'année-lumière, la distance parcourue par la lumière en 1 an, et le parsec (pc), la distance d'une étoile dont la parallaxe est de 1 seconde d'arc (1 parsec = 3,26 années-lumière). L'étoile la plus proche, une naine rouge, se trouve à plus d'un parsec. Les premières mesures réussies des parallaxes stellaires ont été signalées en 1838. Les mesures de parallaxe constituent un maillon fondamental de la chaîne des distances cosmiques. Le satellite Hipparcos nous a permis de mesurer des parallaxes précises pour des étoiles jusqu'à environ 300 années-lumière, et la mission Gaia produira des parallaxes jusqu'à 30 000 années-lumière.

Notes

¹ À titre de comparaison, la planète naine Pluton orbite à une distance moyenne de 40 UA du Soleil, et la planète naine Eris se trouve actuellement à environ 96 UA du Soleil.

² Le mouvement correct (comme indiqué dans Analyzing Starlight) est le mouvement d'une étoile dans le ciel (perpendiculaire à notre ligne de visée).

Lexique

parallaxe

déplacement apparent d'une étoile proche résultant du mouvement de la Terre autour du Soleil

parsec

unité de distance en astronomie, égale à 3,26 années-lumière ; à une distance de 1 parsec, une étoile a une parallaxe de 1 seconde d'arc