17.1 : La luminosité des étoiles

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Expliquer la différence entre la luminosité et la luminosité apparente
• Découvrez comment les astronomes spécifient la luminosité avec des magnitudes

Luminosité

La caractéristique la plus importante d'une étoile est peut-être sa luminosité, c'est-à-dire la quantité totale d'énergie émise par seconde à toutes les longueurs d'onde. Plus tôt, nous avons vu que le Soleil émet une énorme quantité d'énergie chaque seconde. (Et il y a des étoiles bien plus lumineuses que le Soleil là-bas.) Pour faciliter la comparaison entre les étoiles, les astronomes expriment la luminosité des autres étoiles en fonction de la luminosité du Soleil. Par exemple, la luminosité de Sirius est environ 25 fois supérieure à celle du Soleil. Nous utilisons le symbole L _Sun pour indiquer la luminosité du soleil ; par conséquent, celui de Sirius peut être écrit comme 25 litres de _soleil. Dans un chapitre ultérieur, nous verrons que si nous pouvons mesurer la quantité d'énergie émise par une étoile et connaître également sa masse, nous pouvons calculer combien de temps elle peut continuer à briller avant d'épuiser son énergie nucléaire et de commencer à mourir.

Luminosité apparente

Les astronomes prennent soin de faire la distinction entre la luminosité de l'étoile (la production d'énergie totale) et la quantité d'énergie qui atteint nos yeux ou un télescope sur Terre. Les étoiles produisent des radiations de façon démocratique ; elles émettent la même quantité d'énergie dans toutes les directions de l'espace. Par conséquent, seule une infime fraction de l'énergie émise par une étoile atteint réellement un observateur sur Terre. Nous appelons la quantité d'énergie d'une étoile qui atteint une zone donnée (disons, un mètre carré) chaque seconde sur Terre sa luminosité apparente. Si vous regardez le ciel nocturne, vous pouvez voir une large gamme de luminosités apparentes parmi les étoiles. En fait, la plupart des étoiles sont si sombres qu'il faut un télescope pour les détecter.

Si toutes les étoiles avaient la même luminosité, si elles étaient comme des ampoules classiques avec le même rendement lumineux, nous pourrions utiliser la différence de leurs luminosités apparentes pour nous dire quelque chose que nous voulons vraiment savoir : à quelle distance elles se trouvent. Imaginez que vous vous trouvez dans une grande salle de concert ou de bal sombre, à l'exception de quelques douzaines d'ampoules de 25 watts placées dans des luminaires placés autour des murs. Comme ce sont toutes des ampoules de 25 watts, leur luminosité (production d'énergie) est la même. Mais d'où vous vous trouvez dans un coin, ils n'ont pas la même luminosité apparente. Les personnes proches de vous paraissent plus claires (une plus grande partie de leur lumière atteint votre œil), tandis que celles qui sont éloignées semblent plus sombres (leur lumière s'est davantage diffusée avant de vous atteindre). De cette façon, vous pouvez savoir quelles ampoules sont les plus proches de vous. De la même manière, si toutes les étoiles avaient la même luminosité, nous pourrions immédiatement en déduire que les étoiles les plus brillantes se trouvaient à proximité et que les étoiles les plus sombres étaient éloignées.

Pour mieux cerner cette idée, rappelons dans le chapitre Rayonnement et spectres que nous savons exactement comment la lumière s'estompe avec l'augmentation de la distance. L'énergie que nous recevons est inversement proportionnelle au carré de la distance. Si, par exemple, nous avons deux étoiles de la même luminosité et que l'une est deux fois plus éloignée que l'autre, elle paraîtra quatre fois plus faible que l'étoile la plus proche. S'il est trois fois plus éloigné, il aura l'air neuf fois plus faible (trois carrés), et ainsi de suite.

Hélas, les étoiles n'ont pas toutes la même luminosité. (En fait, nous en sommes plutôt contents, car le fait d'avoir de nombreux types d'étoiles différents rend l'univers beaucoup plus intéressant.) Mais cela signifie que si une étoile semble sombre dans le ciel, on ne peut pas dire si elle semble sombre parce qu'elle a une faible luminosité mais qu'elle est relativement proche, ou parce qu'elle a une luminosité élevée mais qu'elle est très éloignée. Pour mesurer les luminosités des étoiles, il faut d'abord compenser les effets de gradation de la distance sur la lumière, et pour cela, nous devons connaître leur distance. La distance est l'une des mesures astronomiques les plus difficiles. Nous reviendrons sur la façon dont elle est déterminée une fois que nous en aurons appris davantage sur les étoiles. Pour l'instant, nous allons décrire comment les astronomes spécifient la luminosité apparente des étoiles.

L'échelle de magnitude

Le processus de mesure de la luminosité apparente des étoiles est appelé photométrie (du grec photo signifiant « lumière » et — métrique signifiant « mesurer »). Comme nous l'avons vu Observation du ciel : la naissance de l'astronomie, la photométrie astronomique a commencé avec Hipparque. Vers 150 avant notre ère, il a érigé un observatoire sur l'île de Rhodes, en Méditerranée. Il y a préparé un catalogue de près de 1 000 étoiles qui comprenait non seulement leurs positions, mais également des estimations de leur luminosité apparente.

Hipparque n'avait pas de télescope ni d'instrument capable de mesurer la luminosité apparente avec précision, il a simplement fait des estimations avec ses yeux. Il a classé les étoiles en six catégories de luminosité, chacune étant appelée magnitude. Il désignait les étoiles les plus brillantes de son catalogue sous le nom d'étoiles de première magnitude, alors que celles qui étaient si faibles qu'il pouvait à peine les voir étaient des étoiles de sixième magnitude. Au cours du XIXe siècle, les astronomes ont tenté de rendre l'échelle plus précise en établissant exactement dans quelle mesure la luminosité apparente d'une étoile de sixième magnitude différait de celle d'une étoile de première magnitude. Les mesures ont montré que nous recevons environ 100 fois plus de lumière d'une étoile de première magnitude que d'une étoile de sixième magnitude. Sur la base de cette mesure, les astronomes ont ensuite défini un système de magnitude précis dans lequel une différence de cinq magnitudes correspond exactement à un rapport de luminosité de 100:1. De plus, les magnitudes des étoiles sont décimales ; par exemple, une étoile n'est pas simplement une « étoile de deuxième magnitude », elle a une magnitude de 2,0 (ou 2,1, 2,3, etc.). Quel est donc ce nombre qui, multiplié cinq fois, vous donne ce facteur de 100 ? Jouez sur votre calculatrice et voyez si vous pouvez l'obtenir. La réponse s'avère être d'environ 2,5, soit la racine 5 de 100. Cela signifie qu'une étoile de magnitude 1,0 et une étoile de magnitude 2,0 diffèrent en termes de luminosité d'un facteur d'environ 2,5. De même, nous recevons environ 2,5 fois plus de lumière d'une étoile de magnitude 2,0 que d'une étoile de magnitude 3,0. Qu'en est-il de la différence entre une étoile de magnitude 1,0 et une étoile de magnitude 3,0 ? Puisque la différence est de 2,5 fois pour chaque « pas » de grandeur, la différence totale de luminosité est de 2,5 × 2,5 = 6,25 fois.

Voici quelques règles de base qui pourraient aider les nouveaux utilisateurs de ce système. Si deux étoiles diffèrent de 0,75 magnitudes, elles diffèrent d'un facteur 2 environ en termes de luminosité. S'ils sont distants de 2,5 magnitudes, leur luminosité diffère d'un facteur 10, et une différence de 4 magnitudes correspond à une différence de luminosité d'un facteur 40. Vous vous demandez peut-être à ce stade : « Pourquoi les astronomes continuent-ils à utiliser ce système complexe d'il y a plus de 2000 ans ? » C'est une excellente question et, comme nous le verrons, les astronomes d'aujourd'hui peuvent utiliser d'autres moyens pour exprimer la luminosité d'une étoile. Mais comme ce système est toujours utilisé dans de nombreux livres, cartes stellaires et applications informatiques, nous avons senti qu'il fallait le présenter aux étudiants (même si nous étions très tentés de le laisser de côté).

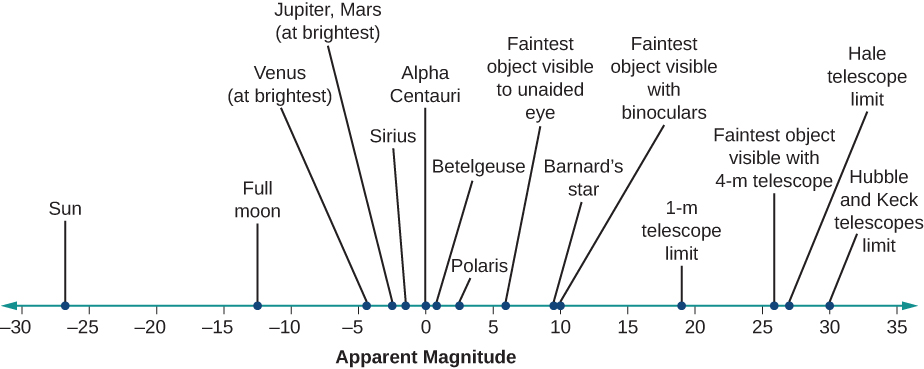
Les étoiles les plus brillantes, celles que l'on appelait traditionnellement étoiles de première magnitude, se sont en fait révélées (lorsqu'elles sont mesurées avec précision) ne pas être identiques en termes de luminosité. Par exemple, l'étoile la plus brillante du ciel, Sirius, nous envoie environ 10 fois plus de lumière qu'une étoile moyenne de première magnitude. Sur l'échelle de magnitude moderne, Sirius, l'étoile dont la magnitude apparente est la plus brillante, s'est vu attribuer une magnitude de −1,5. D'autres objets dans le ciel peuvent paraître encore plus lumineux. À son apogée, Vénus est de magnitude −4,4, tandis que le Soleil a une magnitude de −26,8. La figure\(\PageIndex{1}\) montre la gamme des magnitudes observées, de la plus claire à la plus faible, ainsi que les magnitudes réelles de plusieurs objets connus. L'important à retenir lors de l'utilisation de la magnitude est que le système recule : plus la magnitude est grande, plus l'objet que vous observez est faible.

Figure\(\PageIndex{1}\) : Magnitudes apparentes d'objets connus. Les plus faibles magnitudes pouvant être détectées à l'œil nu, à des jumelles et à de grands télescopes sont également affichées.

Exemple\(\PageIndex{1}\) : L'équation de magnitude

Même les scientifiques ne peuvent pas calculer la cinquième racine de leur tête. Les astronomes ont donc résumé la discussion ci-dessus dans une équation pour aider à calculer la différence de luminosité entre des étoiles de différentes magnitudes. Si m 1 et m 2 sont les magnitudes de deux étoiles, on peut calculer le rapport de leur luminosité à\(\left( \frac{b_2}{b_1} \right)\) l'aide de cette équation :

\[m_1−m_2=2.5 \log \left( \frac{b_2}{b_1} \right) \text{ or } \frac{b_2}{b_1}=2.5^{m_1−m_2} \nonumber\]

Voici une autre façon d'écrire cette équation :

\[\frac{b_2}{b_1}= \left( 100^{0.2} \right)^{m_1−m_2} \nonumber\]

Faisons un exemple concret, juste pour montrer comment cela fonctionne. Imaginez qu'une astronome ait découvert quelque chose de spécial à propos d'une étoile sombre (magnitude 8,5) et qu'elle veuille dire à ses élèves à quel point l'étoile est plus sombre que Sirius. L'étoile 1 de l'équation sera notre étoile sombre et l'étoile 2 sera Sirius.

Solution

N'oubliez pas que Sirius a une magnitude de −1,5. Dans ce cas :

\[\begin{aligned} \frac{b_2}{b_1} & = \left( 100^{0.2} \right)^{8.5−(−1.5)} =\left( 100^{0.2} \right)^{10} \\ ~ & =(100)^2=100×100=10,000 \end{aligned} \nonumber\]

Exercice\(\PageIndex{1}\)

On pense souvent à tort que Polaris (magnitude 2,0) est l'étoile la plus brillante du ciel, mais, comme nous l'avons vu, cette distinction appartient en fait à Sirius (magnitude −1,5). Comment la luminosité apparente de Sirius se compare-t-elle à celle de Polaris ?

Réponse

\[ \frac{b_{\text{Sirius}}}{b_{\text{Polaris}}} = \left( 100^{0.2} \right)^{2.0−(−1.5)} = \left( 100^{0.2} \right)^{3.5} =100^{0.7}=25 \nonumber\]

(Conseil : si vous n'avez qu'une calculatrice de base, vous vous demandez peut-être comment porter la puissance de 100 à 0,7. Mais c'est quelque chose que vous pouvez demander à Google de faire. Google accepte désormais les questions mathématiques et y répondra. Alors essayez-le par vous-même. Demandez à Google : « Qu'est-ce que 100 pour la 0,7 puissance ? »)

Notre calcul montre que la luminosité apparente de Sirius est 25 fois supérieure à la luminosité apparente de Polaris.

Autres unités de luminosité

Bien que l'échelle de magnitude soit toujours utilisée pour l'astronomie visuelle, elle n'est pas du tout utilisée dans les nouvelles branches du domaine. En radioastronomie, par exemple, aucun équivalent du système de magnitude n'a été défini. Les radioastronomes mesurent plutôt la quantité d'énergie collectée chaque seconde par chaque mètre carré d'un radiotélescope et expriment la luminosité de chaque source en termes, par exemple, de watts par mètre carré.

De même, la plupart des chercheurs dans les domaines de l'astronomie infrarouge, des rayons X et des rayons gamma utilisent l'énergie par zone et par seconde plutôt que les magnitudes pour exprimer les résultats de leurs mesures. Néanmoins, les astronomes de tous les domaines prennent soin de faire la distinction entre la luminosité de la source (même lorsque cette luminosité est uniquement exprimée en rayons X) et la quantité d'énergie qui nous parvient sur Terre. Après tout, la luminosité est une caractéristique très importante qui nous en dit long sur l'objet en question, alors que l'énergie qui atteint la Terre est un accident de géographie cosmique.

Pour faciliter la comparaison entre les étoiles, dans ce texte, nous évitons autant que possible d'utiliser des magnitudes et nous exprimerons la luminosité des autres étoiles en termes de luminosité du Soleil. Par exemple, la luminosité de Sirius est 25 fois supérieure à celle du Soleil. Nous utilisons le symbole\(L_{Sun}\) pour indiquer la luminosité du soleil ; par conséquent, celui de Sirius peut être écrit 25\(L_{Sun}\).

Résumé

L'énergie totale émise par seconde par une étoile est appelée luminosité. La luminosité apparente d'une étoile du point de vue de la Terre est son éclat apparent. La luminosité apparente d'une étoile dépend à la fois de sa luminosité et de sa distance par rapport à la Terre. Ainsi, la détermination de la luminosité apparente et la mesure de la distance par rapport à une étoile fournissent suffisamment d'informations pour calculer sa luminosité. La luminosité apparente des étoiles est souvent exprimée en termes de magnitudes, un ancien système basé sur la façon dont la vision humaine interprète l'intensité lumineuse relative.

Lexique

luminosité apparente

une mesure de la quantité de lumière reçue par la Terre en provenance d'une étoile ou d'un autre objet, c'est-à-dire de la luminosité d'un objet dans le ciel, par rapport à sa luminosité

luminosité

la vitesse à laquelle une étoile ou un autre objet émet de l'énergie électromagnétique dans l'espace ; la puissance totale de sortie d'un objet

magnitude

un ancien système de mesure de la quantité de lumière que nous recevons d'une étoile ou d'un autre objet lumineux ; plus l'amplitude est grande, moins nous recevons de rayonnement de l'objet