4.1 : Ciel et Terre
- Page ID
- 192258
Objectifs d'apprentissage
À la fin de cette section, vous serez en mesure de :
- Décrire comment la latitude et la longitude sont utilisées pour cartographier la Terre
- Expliquer comment l'ascension et la déclinaison vers la droite sont utilisées pour cartographier le ciel
Pour créer une carte précise, un cartographe doit pouvoir identifier de manière unique et simple l'emplacement de toutes les principales entités de la carte, telles que les villes ou les sites naturels. De même, les cartographes astronomiques ont besoin d'un moyen unique et simple d'identifier l'emplacement des étoiles, des galaxies et d'autres objets célestes. Sur les cartes de la Terre, nous divisons la surface de la Terre en une grille, et chaque emplacement de cette grille peut être facilement trouvé à l'aide de ses coordonnées de latitude et de longitude. Les astronomes ont un système similaire pour les objets du ciel. L'apprentissage de ces éléments peut nous aider à comprendre le mouvement apparent d'objets dans le ciel provenant de divers endroits de la Terre.
Localiser des lieux sur Terre
Commençons par fixer notre position à la surface de la planète Terre. Comme nous l'avons vu dans Observing the Sky : The Birth of Astronomy, l'axe de rotation de la Terre définit les positions de ses pôles nord et sud et de son équateur, à mi-chemin entre les deux. Deux autres directions sont également définies par les mouvements de la Terre : l'est est est la direction vers laquelle la Terre tourne et l'ouest est son opposé. En tout point de la Terre, les quatre directions (nord, sud, est et ouest) sont bien définies, malgré le fait que notre planète soit ronde plutôt que plate. Les seules exceptions concernent exactement les pôles Nord et Sud, où les directions est et ouest sont ambiguës (car les points situés exactement aux pôles ne tournent pas).
Nous pouvons utiliser ces idées pour définir un système de coordonnées rattaché à notre planète. Un tel système, comme le tracé des rues et des avenues de Manhattan ou de Salt Lake City, nous aide à trouver où nous sommes ou voulons aller. Les coordonnées sur une sphère sont toutefois un peu plus compliquées que celles sur une surface plane. Nous devons définir des cercles sur la sphère qui jouent le même rôle que la grille rectangulaire que vous voyez sur les cartes de la ville.
Un grand cercle est un cercle à la surface d'une sphère dont le centre se trouve au centre de la sphère. Par exemple, l'équateur de la Terre est un grand cercle situé à la surface de la Terre, à mi-chemin entre les pôles Nord et Sud. Nous pouvons également imaginer une série de grands cercles qui traversent à la fois les pôles Nord et Sud. Chacun des cercles est appelé méridien ; ils sont chacun perpendiculaires à l'équateur et le croisent à angle droit.
Tout point de la surface de la Terre sera traversé par un méridien (Figure\(\PageIndex{1}\)). Le méridien indique la position est-ouest, ou longitude, du lieu. Par accord international (et il a fallu de nombreuses réunions pour que les pays du monde se mettent d'accord), la longitude est définie comme le nombre de degrés d'arc le long de l'équateur entre votre méridien et celui passant par Greenwich, en Angleterre, qui a été désigné comme le méridien principal. La longitude du méridien principal est définie comme 0°.
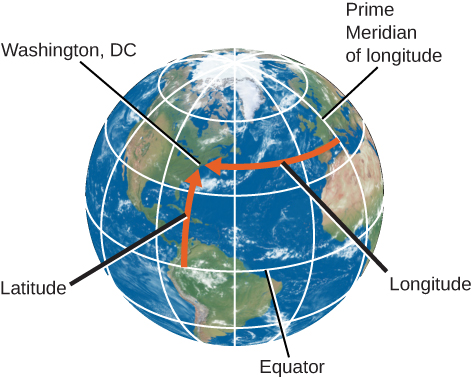
Pourquoi Greenwich, vous vous demandez peut-être ? Chaque pays souhaitait passer par sa propre capitale à 0° de longitude. Greenwich, le site de l'ancien Observatoire royal (Figure\(\PageIndex{2}\)), a été choisi parce qu'il se trouvait entre l'Europe continentale et les États-Unis et parce qu'il a été le site d'une grande partie du développement de la méthode de mesure de la longitude en mer. Les longitudes sont mesurées soit à l'est soit à l'ouest du méridien de Greenwich, de 0° à 180°. À titre d'exemple, la longitude du point de référence de l'horloge de l'Observatoire naval américain à Washington, DC, est de 77,066° O.

Votre latitude (ou position nord-sud) est le nombre de degrés d'arc qui vous séparent de l'équateur le long de votre méridien. Les latitudes sont mesurées au nord ou au sud de l'équateur entre 0° et 90°. (La latitude de l'équateur est de 0°.) À titre d'exemple, la latitude du point de repère de l'observatoire naval mentionné précédemment est de 38,921° N. La latitude du pôle Sud est de 90° S et la latitude du pôle Nord est de 90° N.
Localiser des lieux dans le ciel
Les positions dans le ciel sont mesurées d'une manière très similaire à la façon dont nous mesurons les positions à la surface de la Terre. Cependant, au lieu de la latitude et de la longitude, les astronomes utilisent des coordonnées appelées déclinaison et ascension droite. Pour indiquer la position des objets dans le ciel, il est souvent pratique d'utiliser la sphère céleste fictive. Nous avons vu dans Observing the Sky : The Birth of Astronomy que le ciel semble tourner autour de points situés au-dessus des pôles nord et sud de la Terre, des points du ciel appelés pôle nord céleste et pôle sud céleste. À mi-chemin entre les pôles célestes, et donc à 90° de chaque pôle, se trouve l'équateur céleste, un grand cercle de la sphère céleste situé dans le même plan que l'équateur de la Terre. Nous pouvons utiliser ces marqueurs dans le ciel pour établir un système de coordonnées célestes.
La déclinaison sur la sphère céleste est mesurée de la même manière que la latitude sur la sphère terrestre : depuis l'équateur céleste vers le nord (positif) ou le sud (négatif). Polaris, l'étoile située près du pôle nord céleste, a donc une déclinaison de presque +90°.
L'ascension droite (RA) est comme la longitude, sauf qu'au lieu de Greenwich, le point choisi arbitrairement pour commencer à compter est l'équinoxe de printemps, point du ciel où l'écliptique (la trajectoire du Soleil) traverse l'équateur céleste. La RA peut être exprimée en unités d'angle (degrés) ou en unités de temps. Cela est dû au fait que la sphère céleste semble tourner autour de la Terre une fois par jour alors que notre planète tourne sur son axe. Ainsi, le 360° de RA qu'il faut pour faire le tour de la sphère céleste peut tout aussi bien être réglé sur 24 heures. Chaque arc de 15° est alors égal à 1 heure de temps. Par exemple, les coordonnées célestes approximatives de l'étoile brillante Capella sont RA 5h = 75° et déclinaison +50°.
Une façon de visualiser ces cercles dans le ciel est d'imaginer la Terre comme une sphère transparente sur laquelle les coordonnées terrestres (latitude et longitude) sont peintes de peinture foncée. Imaginez la sphère céleste qui nous entoure sous la forme d'une boule géante, peinte en blanc à l'intérieur. Imaginez-vous ensuite au centre de la Terre, avec une ampoule brillante au milieu, regardant le ciel à travers sa surface transparente. Les pôles terrestres, l'équateur et les méridiens seront projetés sous forme d'ombres sombres sur la sphère céleste, ce qui nous donnera le système de coordonnées dans le ciel.
Vous pouvez découvrir une variété d'animations de base sur les coordonnées et les mouvements dans le ciel sur ce site interactif de ClassAction. Cliquez sur l'onglet « Animations » pour obtenir la liste des options. Si vous choisissez la deuxième option dans le menu, vous pouvez jouer avec la sphère céleste et voir la RA et la déclinaison définies visuellement.
La Terre qui tourne
Pourquoi de nombreuses étoiles se lèvent-elles et se couchent-elles chaque nuit ? En d'autres termes, pourquoi le ciel nocturne semble-t-il tourner ? Nous avons vu que la rotation apparente de la sphère céleste pouvait être expliquée soit par une rotation quotidienne du ciel autour d'une Terre stationnaire, soit par la rotation de la Terre elle-même. Depuis le XVIIe siècle, il est généralement admis que c'est la Terre qui tourne, mais ce n'est qu'au XIXe siècle que le physicien français Jean Foucault a fourni une démonstration sans ambiguïté de cette rotation. En 1851, il a suspendu un pendule de 60 mètres pesant environ 25 kilogrammes au dôme du Panthéon à Paris et a fait osciller le pendule de manière uniforme. Si la Terre n'avait pas tourné, il n'y aurait pas eu de modification du plan d'oscillation du pendule et elle aurait donc continué à suivre la même trajectoire. Pourtant, au bout de quelques minutes, Foucault a pu constater que le plan de mouvement du pendule tournait. Foucault a expliqué que ce n'était pas le pendule qui se déplaçait, mais plutôt la Terre qui tournait en dessous (Figure\(\PageIndex{3}\)). Vous pouvez désormais trouver de tels pendules dans de nombreux centres scientifiques et planétariums du monde entier.

Pouvez-vous trouver d'autres preuves qui indiquent que c'est la Terre et non le ciel qui tourne ? (Voir la section 4.E, Activité de groupe collaborative A à la fin de ce chapitre.)
Concepts clés et résumé
Le système terrestre de latitude et de longitude utilise les grands cercles appelés méridiens. La longitude est fixée arbitrairement à 0° à l'Observatoire royal de Greenwich, en Angleterre. Un système de coordonnées célestes analogue est appelé ascension droite (RA) et déclinaison, avec 0° de déclinaison à partir de l'équinoxe de printemps. Ces systèmes de coordonnées nous aident à localiser n'importe quel objet sur la sphère céleste. Le pendule de Foucault est un moyen de démontrer que la Terre tourne.
Lexique
- déclinaison
- la distance angulaire au nord ou au sud de l'équateur céleste
- grand cercle
- un cercle à la surface d'une sphère qui est la courbe d'intersection de la sphère avec un plan passant par son centre
- méridien
- un grand cercle sur la sphère terrestre ou céleste qui passe par les pôles
- ascension droite
- la coordonnée pour mesurer les positions est-ouest des corps célestes ; l'angle mesuré vers l'est le long de l'équateur céleste entre l'équinoxe de printemps et le cercle des heures traversant un corps


