11.8 : Résoudre des systèmes avec la règle de Cramer
- Page ID
- 194995
- Évaluez les déterminants 2 × 2.
- Utilisez la règle de Cramer pour résoudre un système d'équations à deux variables.
- Évaluez les déterminants 3 × 3.
- Utilisez la règle de Cramer pour résoudre un système de trois équations en trois variables.
- Connaissez les propriétés des déterminants.
Nous avons appris à résoudre des systèmes d'équations à deux variables et à trois variables, et par de multiples méthodes : substitution, addition, élimination gaussienne, utilisation de l'inverse d'une matrice et représentation graphique. Certaines de ces méthodes sont plus faciles à appliquer que d'autres et sont plus appropriées dans certaines situations. Dans cette section, nous allons étudier deux autres stratégies pour résoudre des systèmes d'équations.
Évaluation du déterminant d'une matrice 2 × 2
Un déterminant est un nombre réel qui peut être très utile en mathématiques car il a de multiples applications, telles que le calcul de la surface, du volume et d'autres quantités. Ici, nous utiliserons des déterminants pour déterminer si une matrice est inversible en utilisant les entrées d'une matrice carrée afin de déterminer s'il existe une solution au système d'équations. Cependant, l'une des applications les plus intéressantes est peut-être leur utilisation en cryptographie. Des signaux ou des messages sécurisés sont parfois envoyés codés dans une matrice. Les données ne peuvent être déchiffrées qu'à l'aide d'une matrice inversible et du déterminant. Pour nos besoins, nous nous concentrons sur le déterminant en tant qu'indication de l'invertibilité de la matrice. Le calcul du déterminant d'une matrice implique de suivre les modèles spécifiques décrits dans cette section.
Le déterminant d'une matrice 2 × 2, donné
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
est défini comme

Remarquez le changement de notation. Il existe plusieurs manières d'indiquer le déterminant, y compris\(\det(A)\) et en remplaçant les crochets d'une matrice par des lignes droites\(| A |\).
Détermine le déterminant de la matrice donnée.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Solution
\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]
Utiliser la règle de Cramer pour résoudre un système de deux équations à deux variables
Nous allons maintenant présenter une méthode finale pour résoudre des systèmes d'équations utilisant des déterminants. Connue sous le nom de Règle de Cramer, cette technique remonte au milieu du XVIIIe siècle et doit son nom à son innovateur, le mathématicien suisse Gabriel Cramer (1704-1752), qui l'a introduite en 1750 dans Introduction à l'Analyse des lignes Courbes algébriques. La règle de Cramer est une méthode viable et efficace pour trouver des solutions à des systèmes comportant un nombre arbitraire d'inconnues, à condition que nous ayons le même nombre d'équations que d'inconnues.
La règle de Cramer nous donnera la solution unique à un système d'équations, s'il existe. Toutefois, si le système n'a pas de solution ou un nombre infini de solutions, cela sera indiqué par un déterminant égal à zéro. Pour déterminer si le système est incohérent ou dépendant, une autre méthode, telle que l'élimination, devra être utilisée.
Pour comprendre la règle de Cramer, examinons de près la façon dont nous résolvons des systèmes d'équations linéaires à l'aide d'opérations de base sur les lignes. Prenons l'exemple d'un système de deux équations à deux variables.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Nous éliminons une variable à l'aide d'opérations sur les lignes et résolvons l'autre. Dites que nous souhaitons résoudre\(x\). Si l'équation \ ref {eq2} est multipliée par l'opposé du coefficient de\(y\) dans l'équation \ ref {eq1}, l'équation \ ref {eq1} est multipliée par le coefficient de\(y\) dans l'équation \ ref {eq2}, et que nous ajoutons les deux équations, la variable\(y\) sera éliminée.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Multiply }R_1 \text{ by }b_2 \\ -&\underline{b_1a_2x−b_1b_2y=−b_1c_2} & \text{Multiply }R_2 \text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]
Maintenant, résolvez\(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
De même, pour résoudre\(y\), nous éliminerons\(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x−a_1b_2y=−a_1c_2} & \text{Multiply }R_2 \text{ by }−a_1 \\ & a_2b_1y−a_1b_2y =a_2c_1−a_1c_2 \end{align*}\]
Résoudre pour\(y\) donner
\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Notez que le dénominateur pour les deux\(x\) et\(y\) est le déterminant de la matrice des coefficients.
Nous pouvons utiliser ces formules pour résoudre\(x\) et\(y\), mais la règle de Cramer introduit également une nouvelle notation :
- \(D\):déterminant de la matrice des coefficients
- \(D_x\):déterminant du numérateur dans la solution de\(x\)
\[x=\dfrac{D_x}{D}\]
- \(D_y\):déterminant du numérateur dans la solution de\(y\)
\[y=\dfrac{D_y}{D}\]
La clé de la règle de Cramer consiste à remplacer la colonne variable d'intérêt par la colonne constante et à calculer les déterminants. Nous pouvons ensuite exprimer\(x\) et\(y\) sous la forme d'un quotient de deux déterminants.
LA
La règle de Cramer est une méthode qui utilise des déterminants pour résoudre des systèmes d'équations qui ont le même nombre d'équations que de variables.
Prenons l'exemple d'un système de deux équations linéaires à deux variables.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
La solution utilisant la règle de Cramer est donnée comme
\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0 \end{align}\]
Si nous résolvons pour\(x\), la\(x\) colonne est remplacée par la colonne constante. Si nous résolvons pour\(y\), la\(y\) colonne est remplacée par la colonne constante.
Résolvez le\(2 × 2\) système suivant en utilisant la règle de Cramer.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Solution
Résolvez pour\(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]
Résolvez pour\(y\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align*}\]
La solution est\((2,−3)\).
Utilisez la règle de Cramer pour résoudre le\(2 × 2\) système d'équations.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Réponse
-
\((3,−7)\)
Évaluation du déterminant d'une matrice 3 × 3
Trouver le déterminant d'une matrice 2×2 est simple, mais trouver le déterminant d'une matrice 3×3 est plus compliqué. Une méthode consiste à augmenter la matrice 3×3 en répétant les deux premières colonnes, ce qui donne une matrice 3×5. Ensuite, nous calculons la somme des produits des entrées situées le long de chacune des trois diagonales (du coin supérieur gauche au coin inférieur droit) et soustrayons les produits des entrées situées le long de chacune des trois diagonales (du coin inférieur gauche au coin supérieur droit). Cela est plus facile à comprendre à l'aide d'un visuel et d'un exemple.
Détermine le déterminant de la matrice 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- Complétez\(A\) avec les deux premières colonnes.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- Du coin supérieur gauche vers le coin inférieur droit : multipliez les entrées vers le bas de la première diagonale. Ajoutez le résultat au produit des entrées situées en bas de la deuxième diagonale. Ajoutez ce résultat au produit des entrées situées en bas de la troisième diagonale.
- Du coin inférieur gauche vers le coin supérieur droit : soustrayez le produit des entrées situées en haut de la première diagonale. De ce résultat, soustrayez le produit des entrées situées le long de la deuxième diagonale. De ce résultat, soustrayez le produit des entrées situées en haut de la troisième diagonale.
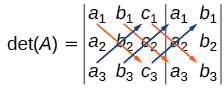
L'algèbre est la suivante :
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Détermine le déterminant de la\(3 × 3\) matrice donnée
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Solution
Augmentez la matrice avec les deux premières colonnes, puis suivez la formule. Ainsi,
\[\begin{align*} | A | &= \left| \begin{array}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{array}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Détermine le déterminant de la matrice 3 × 3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Réponse
-
\(−10\)
Non, cette méthode ne fonctionne que pour les matrices 2 × 2 et 3 × 3. Pour les matrices plus grandes, il est préférable d'utiliser un utilitaire graphique ou un logiciel informatique.
Utiliser la règle de Cramer pour résoudre un système de trois équations en trois variables
Maintenant que nous pouvons trouver le déterminant d'une\(3 × 3\) matrice, nous pouvons appliquer la règle de Cramer pour résoudre un système de trois équations en trois variables. La règle de Cramer est simple et suit un modèle conforme à la règle de Cramer pour les\(2 × 2\) matrices. Cependant\(3 × 3\), à mesure que l'ordre de la matrice augmente, de nombreux autres calculs sont nécessaires.
Lorsque nous calculons le déterminant à zéro, la règle de Cramer ne donne aucune indication quant à savoir si le système n'a pas de solution ou un nombre infini de solutions. Pour le savoir, nous devons effectuer une élimination sur le système.
Envisagez un\(3 × 3\) système d'équations.
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue}d_3 \\ \end{align}\]
\(x=\dfrac{D_x}{D}\)\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\),\(D≠0\)
où
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Si nous écrivons le déterminant\(D_x\), nous remplaçons la\(x\) colonne par la colonne constante. Si nous écrivons le déterminant\(D_y\), nous remplaçons la colonne y par la colonne constante. Si nous écrivons le déterminant\(D_z\), nous remplaçons la\(z\) colonne par la colonne constante. Vérifiez toujours la réponse.
Trouvez la solution au\(3 × 3\) système donné à l'aide de la règle de Cramer.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Solution
Utilisez la règle de Cramer.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\)\(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\\14&3&−2\end{vmatrix}\),\(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\),\(D_z=\begin{vmatrix}1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)
Ensuite,
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
La solution est\((1,3,−2)\).
Utilisez la règle de Cramer pour résoudre la\(3 × 3\) matrice.
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Réponse
-
\(\left(−2,\dfrac{3}{5},\dfrac{12}{5}\right)\)
Résolvez le système d'équations en utilisant la règle de Cramer.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Solution
Nous commençons par trouver les déterminants\(D\)\(D_x\), et\(D_y\).
\(D=\begin{vmatrix}3&−2\\6&−4\end{vmatrix}=3(−4)−6(−2)=0\)
Nous savons qu'un déterminant de zéro signifie soit que le système n'a pas de solution, soit qu'il possède un nombre infini de solutions. Pour savoir lequel, nous utilisons le processus d'élimination. Notre objectif est d'éliminer l'une des variables.
- Multipliez l'équation \ ref {eq3} par\(−2\).
- Ajoutez le résultat à l'équation \ ref {eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\;\;\;\;\; 0=−8 \end{align*}\]
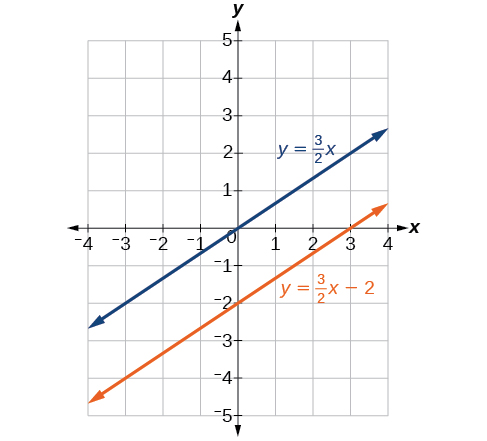
Nous obtenons l'équation\(0=−8\), qui est fausse. Le système n'a donc pas de solution. La représentation graphique du système révèle deux lignes parallèles. Voir la figure\(\PageIndex{1}\).
Résolvez le système avec un nombre infini de solutions.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end{align}\]
Solution
Trouvons d'abord le déterminant. Configurez une matrice augmentée par les deux premières colonnes.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)
Ensuite,
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1)−6(3)(−2)=0\)
Comme le déterminant est égal à zéro, il n'y a pas de solution ou un nombre infini de solutions. Nous devons procéder à une élimination pour le savoir.
1. Multipliez l'équation \ ref {eq5} par\(−2\) et ajoutez le résultat à l'équation \ ref {eq7} :
\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]
2. L'obtention d'une réponse à une affirmation toujours vraie signifie que le système dispose d'un nombre infini de solutions.\(0=0\) En dessinant le système, nous pouvons voir que deux des plans sont identiques et qu'ils croisent tous deux le troisième plan sur une ligne. Voir la figure\(\PageIndex{2}\).
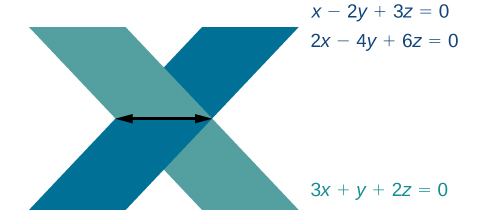
Comprendre les propriétés des déterminants
Les propriétés des déterminants sont nombreuses. Voici quelques propriétés qui peuvent être utiles pour calculer le déterminant d'une matrice.
- Si la matrice se présente sous forme triangulaire supérieure, le déterminant est égal au produit des entrées situées le long de la diagonale principale.
- Lorsque deux lignes sont interchangées, le déterminant change de signe.
- Si deux lignes ou deux colonnes sont identiques, le déterminant est égal à zéro.
- Si une matrice contient une ligne de zéros ou une colonne de zéros, le déterminant est égal à zéro.
- Le déterminant d'une matrice inverse\(A^{−1}\) est l'inverse du déterminant de la matrice\(A\).
- Si une ligne ou une colonne est multipliée par une constante, le déterminant est multiplié par le même facteur.
Illustrez chacune des propriétés des déterminants.
Solution
La propriété 1 indique que si la matrice est sous forme triangulaire supérieure, le déterminant est le produit des entrées situées le long de la diagonale principale.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)
Complétez\(A\) avec les deux premières colonnes.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)
Alors
\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1(0)(2)\\ &= -2 \end{align*}\]
La propriété 2 indique que l'échange de lignes modifie le signe. Donné
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)(5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]
La propriété 3 indique que si deux lignes ou deux colonnes sont identiques, le déterminant est égal à zéro.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{array}\right]\\ \det(A)&=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\\ &=4-4+8+4-4-8\\ &=0 \end{align*}\]
La propriété 4 indique que si une ligne ou une colonne est égale à zéro, le déterminant est égal à zéro. Ainsi,
\[\begin{align*} A&=\begin{bmatrix}1&2\\0&0\end{bmatrix}\\ \det(A)&=1(0)-2(0)\\ &=0 \end{align*}\]
La propriété 5 indique que le déterminant d'une matrice inverse\(A^{−1}\) est l'inverse du déterminant\(A\). Ainsi,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-3(2)\\ &=-2 \end{align*}\]
\[\begin{align*} A^{-1}&=\begin{bmatrix}-2&1\\\dfrac{3}{2}&-\dfrac{1}{2}\end{bmatrix}\\ \det(A^{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \end{align*}\]
La propriété 6 indique que si une ligne ou une colonne d'une matrice est multipliée par une constante, le déterminant est multiplié par le même facteur. Ainsi,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \end{align*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4)\\ &=-4 \end{align*}\]
Trouvez la solution pour le\(3 × 3\) système donné.
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\end{align}\]
Solution
En utilisant la règle de Cramer, nous avons
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Notez que les deuxième et troisième colonnes sont identiques. Selon la propriété 3, le déterminant sera nul, donc il n'y a pas de solution ou un nombre infini de solutions. Nous devons procéder à une élimination pour le savoir.
1. Multipliez l'équation \ ref {eq10} par\(–2\) et ajoutez le résultat à l'équation \ ref {eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
L'obtention d'une déclaration contradictoire signifie que le système n'a pas de solution.
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires avec Cramer's Rule.
Concepts clés
- Le déterminant pour\(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) est\(ad−bc\). Voir l'exemple\(\PageIndex{1}\).
- La règle de Cramer remplace une colonne variable par une colonne constante. Les solutions sont\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\). Voir l'exemple\(\PageIndex{2}\).
- Pour trouver le déterminant d'une\(3×3\) matrice, complétez avec les deux premières colonnes. Ajoutez les trois entrées diagonales (du coin supérieur gauche vers le coin inférieur droit) et soustrayez les trois entrées diagonales (du coin inférieur gauche vers le coin supérieur droit). Voir l'exemple\(\PageIndex{3}\).
- Pour résoudre un système de trois équations en trois variables à l'aide de la règle de Cramer, remplacez une colonne variable par la colonne constante pour chaque solution souhaitée :\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\). Voir l'exemple\(\PageIndex{4}\).
- La règle de Cramer est également utile pour trouver la solution d'un système d'équations sans solution ou sans solutions infinies. Voir Exemple\(\PageIndex{5}\) et Exemple\(\PageIndex{6}\).
- Certaines propriétés des déterminants sont utiles pour résoudre des problèmes. Par exemple :
- Si la matrice se présente sous forme triangulaire supérieure, le déterminant est égal au produit des entrées situées le long de la diagonale principale.
- Lorsque deux lignes sont interchangées, le déterminant change de signe.
- Si deux lignes ou deux colonnes sont identiques, le déterminant est égal à zéro.
- Si une matrice contient une ligne de zéros ou une colonne de zéros, le déterminant est égal à zéro.
- Le déterminant d'une matrice inverse\(A^{−1}\) est l'inverse du déterminant de la matrice\(A\).
- Si une ligne ou une colonne est multipliée par une constante, le déterminant est multiplié par le même facteur. Voir Exemple\(\PageIndex{7}\) et Exemple\(\PageIndex{8}\).


