11.5 : Matrices et opérations matricielles
- Page ID
- 194994
- Détermine la somme et la différence de deux matrices.
- Détermine les multiples scalaires d'une matrice.
- Détermine le produit de deux matrices.
Deux équipes de soccer de club, les Wildcats et les Mud Cats, espèrent obtenir de nouveaux équipements pour la saison à venir. Le tableau\(\PageIndex{1}\) montre les besoins des deux équipes.
| Wildcats | Chats de boue | |
|---|---|---|
| Objectifs | 6 | 10 |
| Ballons | 30 | 24 |
| Maillots | 14 | 20 |
Un but coûte\($300\), un ballon coûte\($10\) et un maillot coûte\($30\). Comment connaître le coût total de l'équipement nécessaire à chaque équipe ? Dans cette section, nous découvrons une méthode permettant d'afficher les données du tableau des équipements de football et de les utiliser pour calculer d'autres informations. Ensuite, nous pourrons calculer le coût de l'équipement.

Déterminer la somme et la différence de deux matrices
Pour résoudre un problème comme celui décrit pour les équipes de football, nous pouvons utiliser une matrice, qui est un tableau rectangulaire de nombres. Une ligne d'une matrice est un ensemble de nombres alignés horizontalement. Une colonne d'une matrice est un ensemble de nombres alignés verticalement. Chaque nombre est une entrée, parfois appelée élément, de la matrice. Les matrices (pluriel) sont placées entre [] ou () et sont généralement nommées en majuscules. Par exemple, trois matrices nommées\(A\)\(B\), et\(C\) sont présentées ci-dessous.
\[ \begin{align*} A&=\begin{bmatrix} 1& 2 \\ 3 & 4 \\ \end{bmatrix} \\[4pt] B &=\begin{bmatrix} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \end{bmatrix} \\[4pt] C &=\begin{bmatrix} -1 & 3 \\ 0 & 2 \\ 3 & 1 \end{bmatrix} \end{align*}\]
Une matrice est souvent désignée par sa taille ou ses dimensions : elle\(m×n\) indique\(m\) les lignes et\(n\) les colonnes. Les entrées de la matrice sont définies d'abord par ligne, puis par colonne. Par exemple, pour localiser l'entrée dans la matrice\(A\) identifiée comme\(a_{ij}\), nous recherchons l'entrée en ligne\(i\), en colonne\(j\). Dans la matrice\(A\), illustrée ci-dessous, l'entrée dans la ligne\(2\), la colonne\(3\) est\(a_{23}\).
\[A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix} \nonumber\]
- Une matrice carrée est une matrice avec des dimensions\(n × n\), c'est-à-dire qu'elle comporte le même nombre de lignes que de colonnes. La\(3×3\) matrice ci-dessus est un exemple de matrice carrée.
- Une matrice de lignes est une matrice composée d'une ligne avec des dimensions\(1 × n\). \[\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix} \nonumber\]
- Une matrice à colonnes est une matrice composée d'une colonne avec des dimensions\(m × 1\). \[\begin{bmatrix} a_{11} \\ a_{21} \\a_{31} \end{bmatrix} \nonumber\]
Une matrice peut être utilisée pour représenter un système d'équations. Dans ces cas, les nombres représentent les coefficients des variables du système. Les matrices facilitent souvent la résolution de systèmes d'équations car ils ne sont pas encombrés de variables. Nous étudierons cette idée plus en détail dans la section suivante, mais nous examinerons d'abord les opérations matricielles de base.
Une matrice est un tableau rectangulaire de nombres qui est généralement nommé par une lettre majuscule :\(A\),,\(B\)\(C\), et ainsi de suite. Chaque entrée d'une matrice est appelée\(a_{ij}\), de telle sorte que cela\(i\) représente la ligne et\(j\) la colonne. Les matrices sont souvent désignées par leurs dimensions : elles\(m × n\) indiquent des\(m\) lignes et des\(n\) colonnes.
Matrice donnée\(A\) :
- Quelles sont les dimensions de la matrice\(A\) ?
- Quelles sont les entrées à\(a_{31}\) et\(a_{22}\) ?
\[A=\begin{bmatrix} 2 & 1 & 0\\2 & 4 & 7\\3 & 1 & −2 \end{bmatrix} \nonumber\]
Solution
- Les dimensions sont dues au\(3 \times 3\) fait qu'il y a trois lignes et trois colonnes.
- L'entrée\(a_{31}\) est le numéro de la ligne 3, colonne 1, qui est\(3\). L'entrée\(a_{22}\) est le numéro de la ligne 2, colonne 2, qui est\(4\). N'oubliez pas que la ligne vient en premier, puis la colonne.
Ajouter et soustraire des matrices
Nous utilisons des matrices pour répertorier des données ou pour représenter des systèmes. Comme les entrées sont des nombres, nous pouvons effectuer des opérations sur des matrices. Nous ajoutons ou soustrayons des matrices en ajoutant ou en soustrayant les entrées correspondantes. Pour ce faire, les entrées doivent correspondre. Par conséquent, l'addition et la soustraction de matrices ne sont possibles que lorsque les matrices ont les mêmes dimensions. Nous pouvons ajouter ou soustraire une\(3 \times 3\) matrice et une autre\(3 \times 3\) matrice, mais nous ne pouvons pas ajouter ou soustraire une\(2 \times 3\) matrice et une\(3 \times 3\) matrice car certaines entrées d'une matrice n'auront pas d'entrée correspondante dans l'autre matrice.
Des matrices données\(A\) et\(B\) de dimensions similaires, l'addition et la soustraction de\(A\) et\(B\) produiront une matrice\(C\) ou une matrice\(D\) de même dimension.
\[A+B=C\]
tel que\(a_{ij}+b_{ij}=c_{ij}\)
\[A−B=D\]
tel que\(a_{ij}−b_{ij}=d_{ij}\)
L'addition de matrices est commutative.
\[A+B=B+A\]
Elle est également associative.
\[(A+B)+C=A+(B+C)\]
Trouve la somme de\(A\) et\(B\), donnée
\[A=\begin{bmatrix}a & b\\c & d \end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber\]
Solution
Ajoutez les entrées correspondantes.
\[\begin{align} A+B &=\begin{bmatrix}a & b\\c & d\end{bmatrix}+\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}a+e & b+f\\c+g & d+h \end{bmatrix} \nonumber \end{align} \nonumber\]
Trouvez la somme de\(A\) et\(B\).
\[A=\begin{bmatrix}4 &1\\3 & 2 \end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}5 & 9\\0 & 7\end{bmatrix} \nonumber\]
Solution
Ajoutez les entrées correspondantes. Ajoutez l'entrée de la ligne 1, colonne 1,\(a_{11}\), de la matrice\(A\) à l'entrée de la ligne 1, colonne 1\(b_{11}\), de\(B\). Continuez le modèle jusqu'à ce que toutes les entrées soient ajoutées.
\[\begin{align} A+B &=\begin{bmatrix}4&1\\3 &2\end{bmatrix}+\begin{bmatrix}5&9\\0&7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}4+5&1+9\\3+0&2+7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}9&10\\3&9\end{bmatrix} \nonumber \end{align} \nonumber\]
Trouvez la différence entre\(A\) et\(B\).
\(A=\begin{bmatrix}−2&3\\0&1\end{bmatrix}\)et\(B=\begin{bmatrix}8&1\\5&4\end{bmatrix}\)
Solution
Nous soustrayons les entrées correspondantes de chaque matrice.
\[\begin{align} A−B &=\begin{bmatrix}−2&3\\0&1\end{bmatrix}−\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−2−8&3−1\\0−5&1−4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−10&2\\−5&−3\end{bmatrix} \nonumber \end{align} \nonumber\]
Donné\(A\) et\(B\) :
- Trouvez la somme.
- Trouvez la différence.
\[A=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber\]
Solution
- Ajoutez les entrées correspondantes.
\[\begin{align} A+B & =\begin{bmatrix} 2& −10& −2\\14 & 12 & 10\\4 & −2 & 2\end{bmatrix}+\begin{bmatrix}6 & 10 & −2\\0 & −12 & −4\\−5 & 2 & −2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+6 & −10+10 & −2−2\\14+0 & 12−12 & 10−4\\4−5 & −2+2 & 2−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix} 8 & 0 & −4\\14 & 0 & 6\\−1 & 0 & 0\end{bmatrix} \nonumber \end{align} \nonumber\]
- Soustrayez les entrées correspondantes.
\[\begin{align} A−B &=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix}−\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2−6 & −10−10 & −2+2\\14−0 & 12+12 & 10+4\\4+5 & −2−2 & 2+2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−4 & −20 & 0\\14 & 24 & 14\\9 & −4 & 4\end{bmatrix} \nonumber \end{align} \nonumber\]
Ajoutez une matrice\(A\) et une matrice\(B\).
\[A=\begin{bmatrix}2&6\\1&0\\1&−3\end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}3&−2\\1&5\\−4&3\end{bmatrix} \nonumber\]
- Réponse
-
\[\begin{align} A+B&=\begin{bmatrix}2&6\\ 1 &0\\1&−3\end{bmatrix}+\begin{bmatrix} 3&-2 \\1&5 \\-4&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+3&6+(−2)\\1+1&0+5\\1+(-4)&−3+3\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}5&4\\2&5\\-3&0\end{bmatrix} \nonumber \end{align} \nonumber\]
Trouver les multiples scalaires d'une matrice
Outre l'addition et la soustraction de matrices entières, il existe de nombreuses situations dans lesquelles nous devons multiplier une matrice par une constante appelée scalaire. Rappelez-vous qu'un scalaire est une quantité numérique réelle qui a une amplitude, mais pas une direction. Par exemple, le temps, la température et la distance sont des quantités scalaires. Le processus de multiplication scalaire consiste à multiplier chaque entrée d'une matrice par un scalaire. Un multiple scalaire est toute entrée d'une matrice résultant d'une multiplication scalaire.
Envisagez un scénario réel dans lequel une université doit augmenter son inventaire d'ordinateurs, de tables d'ordinateur et de chaises dans deux des laboratoires du campus en raison de l'augmentation du nombre d'inscriptions. Ils estiment que des équipements\(15%\) supplémentaires sont nécessaires dans les deux laboratoires. L'inventaire actuel de l'école est affiché dans le tableau\(\PageIndex{2}\).
| Laboratoire A | Labo B | |
|---|---|---|
| Ordinateurs | 15 | 27 |
| Tables d'ordinateur | 16 | 34 |
| chaises | 16 | 34 |
En convertissant les données en matrice, nous avons
\[C_{2013}=\begin{bmatrix}15 & 27\\16&34\\16&34\end{bmatrix} \nonumber\]
Pour calculer la quantité d'équipement informatique nécessaire, nous multiplions toutes les entrées de la matrice\(C\) par\(0.15\).
\[(0.15)C_{2013}=\begin{bmatrix}(0.15)15&(0.15)27\\(0.15)16&(0.15)34\\(0.15)16 &(0.15)34\end{bmatrix}=\begin{bmatrix}2.25 &4.05\\2.4&5.1\\2.4&5.1\end{bmatrix} \nonumber\]
Nous devons arrondir au nombre entier suivant, de sorte que la quantité de nouveaux équipements nécessaires soit
\[\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix} \nonumber\]
En ajoutant les deux matrices comme indiqué ci-dessous, nous voyons les nouvelles quantités d'inventaire.
\[\begin{bmatrix}15&27\\16&34\\16&34\end{bmatrix}+\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Cela signifie
\[C_{2014}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Ainsi, le laboratoire A disposera d'\(18\)ordinateurs, de tables d'\(19\)ordinateur et de\(19\) chaises ; le laboratoire B aura des\(32\) ordinateurs, des tables d'\(40\)ordinateur et\(40\) des chaises.
La multiplication scalaire consiste à trouver le produit d'une constante par chaque entrée de la matrice. Donné
\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
le multiple scalaire\(cA\) est
\[cA=c\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
\[=\begin{bmatrix}ca_{11}&ca_{12}\\ca_{21}&ca_{22}\end{bmatrix} \nonumber\]
La multiplication scalaire est distributive. Pour les matrices\(A\)\(B\), et\(C\) avec des scalaires\(a\) et\(b\),
\[a(A+B)=aA+aB\]
\[(a+b)A=aA+bA\]
Multipliez la matrice\(A\) par le scalaire\(3\).
\[A=\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber\]
Solution
Multipliez chaque entrée\(A\) par le scalaire\(3\).
\[ \begin{align} 3A&=3\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3⋅8&3⋅1\\3⋅5&3⋅4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}24&3\\15&12\end{bmatrix} \nonumber \end{align} \nonumber\]
Matrice donnée\(B\), trouvez\(−2B\) où
\[B=\begin{bmatrix}4&1\\3&2\end{bmatrix} \nonumber\]
- Réponse
-
\[−2B=\begin{bmatrix}−8&−2\\−6&−4\end{bmatrix} \nonumber\]
Trouve la somme\(3A+2B\).
\[A=\begin{bmatrix}1&−2&0\\0&−1&2\\4&3&−6\end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}−1&2&1\\0&−3&2\\0&1&−4\end{bmatrix} \nonumber\]
Solution
D'abord, trouvez\(3A\), ensuite\(2B\).
\[ \begin{align} 3A&=\begin{bmatrix}3⋅1&3(−2)&3⋅0\\3⋅0&3(−1)&3⋅2\\3⋅4&3⋅3&3(−6)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}\nonumber \end{align} \nonumber\]
\[ \begin{align} 2B&=\begin{bmatrix}2(−1)&2⋅2&2⋅1\\2⋅0&2(−3)&2⋅2\\2⋅0&2⋅1&2(−4)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix}\nonumber \end{align} \nonumber\]
Maintenant, ajoutez\(3A+2B\).
\[ \begin{align} 3A+2B&=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}+\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3−2&−6+4&0+2\\0+0&−3−6&6+4\\12+0&9+2&−18−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1& −2&2\\0&−9&10\\12&11&−26\end{bmatrix} \nonumber \end{align} \nonumber\]
Trouver le produit de deux matrices
En plus de multiplier une matrice par un scalaire, nous pouvons multiplier deux matrices. Trouver le produit de deux matrices n'est possible que lorsque les dimensions intérieures sont les mêmes, c'est-à-dire que le nombre de colonnes de la première matrice est égal au nombre de lignes de la seconde matrice. Si\(A\) c'est une\(m × r\) matrice et\(B\) est une\(r × n\) matrice, alors la matrice du produit\(AB\) est une\(m × n\) matrice. Par exemple, le produit\(AB\) est possible car le nombre de colonnes\(A\) est identique au nombre de lignes\(B\). Si les dimensions intérieures ne correspondent pas, le produit n'est pas défini.
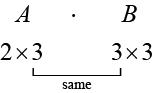
Nous multiplions les entrées\(A\) de par les entrées de\(B\) selon un modèle spécifique, comme indiqué ci-dessous. Le processus de multiplication matricielle devient plus clair lorsque l'on traite d'un problème avec des nombres réels.
Pour obtenir les entrées de la ligne\(i\) de\(AB\), nous multiplions les entrées de la ligne\(A\) par\(i\) la colonne\(B\) et\(j\) les additionnons. Par exemple, des matrices données\(A\) et\(B\), où les dimensions de\(A\) sont\(2 \times 3\) et les dimensions de\(B\) sont\(3 \times 3\), le produit de\(AB\) sera une\(2 \times 3\) matrice.
\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix} \nonumber \]
et
\[B=\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix} \nonumber\]
Multipliez et additionnez comme suit pour obtenir la première entrée de la matrice du produit\(AB\).
- Pour obtenir l'entrée dans la ligne 1, colonne 1 de\(AB\), multipliez la première ligne\(A\) par la première colonne dans\(B\), puis additionnez.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}=a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} \nonumber \]
- Pour obtenir l'entrée dans la ligne 1, colonne 2 de\(AB\), multipliez la première ligne de\(A\) par la deuxième colonne et additionnez.\(B\)
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{12}\\b_{22}\\b_{32}\end{bmatrix}=a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32} \nonumber \]
- Pour obtenir l'entrée dans la ligne 1, colonne 3 de\(AB\), multipliez la première ligne de\(A\) par la troisième colonne et additionnez.\(B\)
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{13}\\b_{23}\\b_{33}\end{bmatrix}=a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \nonumber \]
Nous procédons de la même manière pour obtenir la deuxième ligne de\(AB\). En d'autres termes, la ligne 2 de\(A\) fois la colonne 1 de\(B\) ; la ligne 2 de\(A\) fois la colonne 2 de\(B\) ; la ligne 2 de\(A\) fois la colonne 3 de\(B\). Une fois terminée, la matrice des produits sera
\[AB=\begin{bmatrix}a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} &a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32}&a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \\a_{21}⋅b_{11}+a_{22}⋅b_{21}+a_{23}⋅b_{31}&a_{21}⋅b_{12}+a_{22}⋅b_{22}+a_{23}⋅b_{32}&a_{21}⋅b_{13}+a_{22}⋅b_{23}+a_{23}⋅b_{33}\end{bmatrix} \nonumber\]
Pour la matrice\(A, B\),\(C\) les propriétés suivantes sont valables.
- La multiplication matricielle est associative :\[(AB)C=A(BC).\]
- La multiplication matricielle est distributive :\[C(A+B)=CA+CB\]\[(A+B)C=AC+BC.\]
Notez que la multiplication matricielle n'est pas commutative.
Multipliez matrice\(A\) et matrice\(B\).
\[A=\begin{bmatrix}1&2\\3&4\end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}5&6\\7&8\end{bmatrix} \nonumber\]
Solution
Tout d'abord, nous vérifions les dimensions des matrices. La matrice\(A\) a\(2 × 2\) des dimensions et la matrice\(B\) a des dimensions\(2 × 2\). Les dimensions intérieures sont les mêmes afin que nous puissions effectuer la multiplication. Le produit aura les dimensions\(2 × 2\).
Nous effectuons les opérations décrites précédemment.
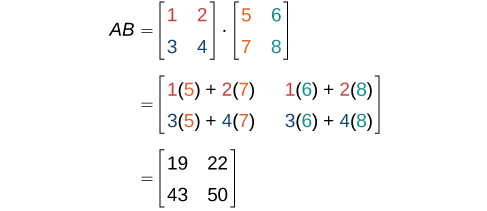
Donné\(A\) et\(B\) :
- Trouvez\(AB\).
- Trouvez\(BA\).
\[A=\begin{bmatrix}−1&2&3\\ 4&0&5\end{bmatrix} \nonumber\]
et
\[B=\begin{bmatrix}5&−1\\-4&0\\2&3\end{bmatrix} \nonumber\]
Solution
- Comme les dimensions de\(A\) sont\(2 \times 3\) et les dimensions de\(B\) sont\(3 \times 2\), ces matrices peuvent être multipliées ensemble car le nombre de colonnes\(A\) correspond au nombre de lignes qu'elles contiennent\(B\). Le produit obtenu sera une\(2 \times 2\) matrice, dont le nombre de lignes est fonction du nombre de colonnes\(B\).\(A\)
\[ \begin{align}AB&=\begin{bmatrix}−1&2&3\\4&0&5\end{bmatrix} \begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−1(5)+2(−4)+3(2)&−1(−1)+2(0)+3(3)\\4(5)+0(−4)+5(2)&4(−1)+0(0)+5(3)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−7&10\\30&11\end{bmatrix} \nonumber \end{align} \nonumber\]
- Les dimensions de\(B\) sont\(3 \times 2\) et les dimensions de\(A\) sont\(2 \times 3\). Les dimensions intérieures correspondent, de sorte que le produit est défini et constituera une\(3 \times 3\) matrice.
\[ \begin{align}BA&=\begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \begin{bmatrix} −1&2&3\\4&0&5\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}5(−1)+−1(4)&5(2)+−1(0)&5(3)+−1(5)\\−4(−1)+0(4)&−4(2)+0(0)&−4(3)+0(5)\\2(−1)+3(4)& 2(2)+3(0)&2(3)+3(5)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix} \nonumber \end{align} \nonumber\]
Analyse
Notez que les produits\(AB\) et\(BA\) les produits ne sont pas égaux.
\[AB=\begin{bmatrix}−7&10\\30&11\end{bmatrix}≠ \begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix}=BA \nonumber\]
Cela montre que la multiplication matricielle n'est pas commutative.
Oui, considérez une matrice\(A\) avec dimension\(3 × 4\) et une matrice\(B\) avec dimension\(4 × 2\). Pour le produit,\(AB\) les dimensions intérieures sont définies\(4\) et le produit est défini, mais pour le produit,\(BA\) les dimensions intérieures le sont\(2\) et le produit n'est\(3\) donc pas défini.
Revenons au problème présenté à l'ouverture de cette section. Nous avons un tableau\(\PageIndex{3}\) qui représente les besoins en équipement de deux équipes de football.
| Wildcats | Chats de boue | |
|---|---|---|
| Objectifs | 6 | 10 |
| Ballons | 30 | 24 |
| Maillots | 14 | 20 |
On nous donne également les prix de l'équipement, comme indiqué dans le tableau\(\PageIndex{4}\).
| Objectif | 300$ |
| Ballon | 10$ |
| Jersey | 30$ |
Nous allons convertir les données en matrices. Ainsi, la matrice des besoins en équipement s'écrit comme suit :
\[E=\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber\]
La matrice des coûts est écrite sous la forme
\[C=\begin{bmatrix}300&10&30\end{bmatrix} \nonumber\]
Nous effectuons une multiplication matricielle pour obtenir les coûts de l'équipement.
\[ \begin{align} CE&=\begin{bmatrix}300&10&30\end{bmatrix}⋅\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}300(6)+10(30)+30(14)&300(10)+10(24)+30(20)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}2,520&3,840\end{bmatrix} \nonumber \end{align} \nonumber\]
Le coût total de l'équipement pour les Wildcats est de\($2,520\), et le coût total de l'équipement pour les Mud Cats est de\($3,840\).
- Enregistrer chaque matrice en tant que variable matricielle\([A], [B], [C],...\)
- Entrez l'opération dans la calculatrice, en appelant chaque variable matricielle selon les besoins.
- Si l'opération est définie, le calculateur présentera la matrice de solutions ; si l'opération n'est pas définie, il affichera un message d'erreur.
Trouver\(AB−C\) donné
\(A=\begin{bmatrix}−15&25&32\\41&−7&−28\\10&34&−2\end{bmatrix}\)\(B=\begin{bmatrix}45&21&−37\\−24&52&19\\6&−48&−31\end{bmatrix}\), et\(C=\begin{bmatrix}−100&−89&−98\\25&−56&74\\−67&42&−75\end{bmatrix}\)
Solution
Sur la page matrice du calculateur, nous saisissons la matrice\(A\) ci-dessus en tant que variable matricielle\([ A ]\), la matrice\(B\) ci-dessus en tant que variable\([ B ]\) matricielle et la matrice\(C\) ci-dessus en tant que variable matricielle\([ C ]\).
Sur l'écran d'accueil de la calculatrice, nous saisissons le problème et appelons chaque variable matricielle selon les besoins.
\[[A]×[B]−[C] \nonumber\]
Le calculateur nous donne la matrice suivante.
\[\begin{bmatrix}−983&−462&136\\1,820&1,897&−856\\−311&2,032&413\end{bmatrix} \nonumber\]
Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires sur les matrices et les opérations matricielles.
Concepts clés
- Une matrice est un ensemble rectangulaire de nombres. Les entrées sont organisées en lignes et en colonnes.
- Les dimensions d'une matrice font référence au nombre de lignes et au nombre de colonnes. Une\(3×2\) matrice comporte trois lignes et deux colonnes. Voir l'exemple\(\PageIndex{1}\).
- Nous ajoutons et soustrayons des matrices de dimensions égales en ajoutant et en soustrayant les entrées correspondantes de chaque matrice. Voir Exemple\(\PageIndex{2}\), Exemple\(\PageIndex{3}\)\(\PageIndex{4}\), Exemple et Exemple\(\PageIndex{5}\).
- La multiplication scalaire consiste à multiplier chaque entrée d'une matrice par une constante. Voir l'exemple\(\PageIndex{6}\).
- Une multiplication scalaire est souvent requise avant que l'addition ou la soustraction ne se produise. Voir l'exemple\(\PageIndex{7}\).
- La multiplication de matrices est possible lorsque les dimensions intérieures sont identiques : le nombre de colonnes de la première matrice doit correspondre au nombre de lignes de la seconde.
- Le produit de deux matrices,\(A\) et\(B\), est obtenu en multipliant chaque entrée de la ligne 1 de\(A\) par chaque entrée de la colonne 1 de\(B\) ; puis multipliez chaque entrée de la ligne 1 de\(A\) par chaque entrée des colonnes 2 de\(B\), et ainsi de suite. Voir Exemple\(\PageIndex{8}\) et Exemple\(\PageIndex{9}\).
- De nombreux problèmes du monde réel peuvent souvent être résolus à l'aide de matrices. Voir l'exemple\(\PageIndex{10}\).
- Nous pouvons utiliser un calculateur pour effectuer des opérations matricielles après avoir enregistré chaque matrice en tant que variable matricielle. Voir l'exemple\(\PageIndex{11}\).


