11.3 : Systèmes d'équations et d'inégalités non linéaires - Deux variables
- Page ID
- 195088
- Résolvez un système d'équations non linéaires par substitution.
- Résolvez un système d'équations non linéaires par élimination.
- Représentez graphiquement une inégalité non linéaire.
- Tracez un système d'inégalités non linéaires.
La comète de Halley (Figure\(\PageIndex{1}\)) tourne autour du soleil environ une fois par\(75\) an. Sa trajectoire peut être considérée comme une ellipse très allongée. D'autres comètes suivent des trajectoires similaires dans l'espace. Ces trajectoires orbitales peuvent être étudiées à l'aide de systèmes d'équations. Ces systèmes sont toutefois différents de ceux que nous avons examinés dans la section précédente parce que les équations ne sont pas linéaires.

Figure\(\PageIndex{1}\) : Comète de Halley (crédit : « NASA Blueshift » /Flickr)
Dans cette section, nous examinerons l'intersection d'une parabole et d'une ligne, d'un cercle et d'une ligne, et d'un cercle et d'une ellipse. Les méthodes de résolution des systèmes d'équations non linéaires sont similaires à celles des équations linéaires.
Résolution d'un système d'équations non linéaires par substitution
Un système d'équations non linéaires est un système de deux équations ou plus dans deux variables ou plus contenant au moins une équation qui n'est pas linéaire. Rappelons qu'une équation linéaire peut prendre la forme\(Ax+By+C=0\). Toute équation qui ne peut pas être écrite sous cette forme en mode non linéaire. La méthode de substitution que nous avons utilisée pour les systèmes linéaires est la même que celle que nous utiliserons pour les systèmes non linéaires. Nous résolvons une équation pour une variable, puis nous substituons le résultat dans la deuxième équation pour résoudre une autre variable, et ainsi de suite. Il existe toutefois une variation dans les résultats possibles.
Intersection d'une parabole et d'une ligne
Il existe trois types de solutions possibles pour un système d'équations non linéaires impliquant une parabole et une droite.
La figure\(\PageIndex{2}\) illustre des ensembles de solutions possibles pour un système d'équations impliquant une parabole et une droite.
- Aucune solution - La ligne ne croisera jamais la parabole.
- Une solution - La ligne est tangente à la parabole et coupe la parabole exactement en un point.
- Deux solutions - La ligne se croise à l'intérieur de la parabole et coupe la parabole en deux points.
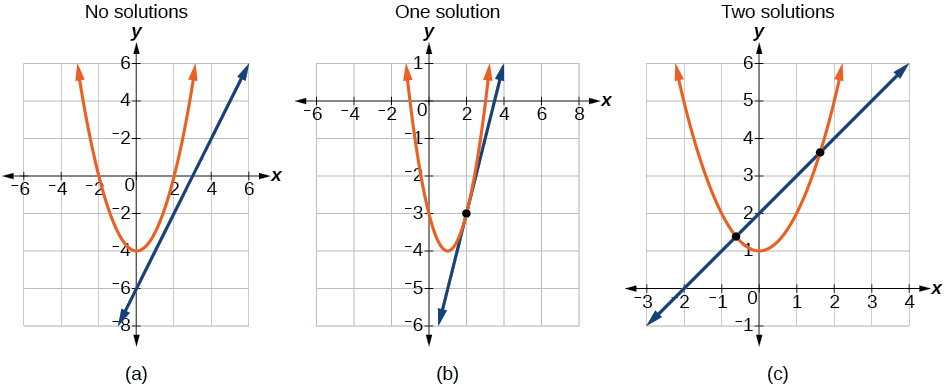
Figurine\(\PageIndex{2}\)
- Résolvez l'équation linéaire pour l'une des variables.
- Substituez l'expression obtenue à la première étape dans l'équation parabolique.
- Résolvez pour la variable restante.
- Vérifiez vos solutions dans les deux équations.
Résolvez le système d'équations.
\[\begin{align*} x−y &= −1\nonumber \\ y &= x^2+1 \nonumber \end{align*}\]
Solution
Résolvez la première équation\(x\) et remplacez-la par l'expression résultante dans la deuxième équation.
\[\begin{align*} x−y &=−1\nonumber \\ x &= y−1 \;\; & \text{Solve for }x.\nonumber \\\nonumber \\ y &=x^2+1\nonumber \\ y & ={(y−1)}^2+1 \;\; & \text{Substitute expression for }x. \nonumber \end{align*}\]
Développez l'équation et mettez-la à zéro.
\[ \begin{align*} y & ={(y−1)}^2+1\nonumber \\ &=(y^2−2y+1)+1\nonumber \\ &=y^2−2y+2\nonumber \\ 0 &= y^2−3y+2\nonumber \\ &= (y−2)(y−1) \nonumber \end{align*}\]
Résoudre pour\(y\) donner\(y=2\) et\(y=1\). Ensuite, remplacez chaque valeur par\(y\) dans la première équation à résoudre\(x\). Remplacez toujours la valeur dans l'équation linéaire pour vérifier la présence de solutions superflues.
\[\begin{align*} x−y &=−1\nonumber \\ x−(2) &= −1\nonumber \\ x &= 1\nonumber \\ x−(1) &=−1\nonumber \\ x &= 0 \nonumber \end{align*}\]
Les solutions sont\((1,2)\) et\((0,1)\), ce qui peut être vérifié en substituant ces\((x,y)\) valeurs dans les deux équations d'origine (Figure\(\PageIndex{3}\)).
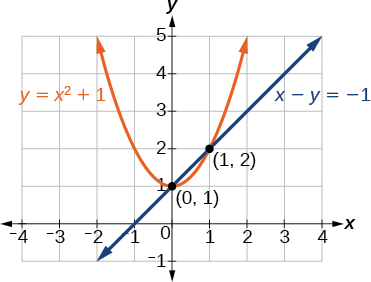
Figurine\(\PageIndex{3}\)
Oui, mais comme il\(x\) est au carré dans la deuxième équation, cela pourrait nous donner des solutions superflues pour\(x\).
Pour\(y=1\)
\[\begin{align*} y &= x^2+1\nonumber \\ y &= x^2+1\nonumber \\ x^2 &= 0\nonumber \\ x &= \pm \sqrt{0}=0 \nonumber \end{align*}\]
Cela nous donne la même valeur que dans la solution.
Pour\(y=2\)
\[\begin{align*} y &= x^2+1\nonumber \\ 2 &= x^2+1\nonumber \\ x^2 &= 1\nonumber \\ x &= \pm \sqrt{1}=\pm 1 \nonumber \end{align*}\]
Notez qu'il\(−1\) s'agit d'une solution superflue.
Résolvez le système d'équations donné par substitution.
\[\begin{align*} 3x−y &= −2\nonumber \\ 2x^2−y &= 0 \nonumber \end{align*}\]
- Réponse
-
\(\left(−\dfrac{1}{2},\dfrac{1}{2}\right)\)et\((2,8)\)
Intersection d'un cercle et d'une ligne
Tout comme pour une parabole et une droite, il existe trois résultats possibles lors de la résolution d'un système d'équations représentant un cercle et une droite.
La figure\(\PageIndex{4}\) illustre des ensembles de solutions possibles pour un système d'équations impliquant un cercle et une ligne.
- Aucune solution - La ligne ne coupe pas le cercle.
- Une solution : la ligne est tangente au cercle et coupe le cercle en un point précis.
- Deux solutions - La ligne traverse le cercle et le croise en deux points.

Figurine\(\PageIndex{4}\)
- Résolvez l'équation linéaire pour l'une des variables.
- Substituez l'expression obtenue à la première étape dans l'équation du cercle.
- Résolvez pour la variable restante.
- Vérifiez vos solutions dans les deux équations.
Trouve l'intersection du cercle donné et de la ligne donnée par substitution.
\[\begin{align*} x^2+y^2 &= 5\nonumber \\ y &= 3x−5 \nonumber \end{align*}\]
Solution
L'une des équations a déjà été résolue pour\(y\). Nous allons remplacer le cercle\(y=3x−5\) dans l'équation.
\[\begin{align*} x^2+{(3x−5)}^2 &= 5\nonumber \\ x^2+9x^2−30x+25 &= 5\nonumber \\ 10x^2−30x+20 &= 0 \end{align*} \]
Maintenant, nous prenons en compte et résolvons\(x\).
\[\begin{align*} 10(x2−3x+2) &= 0\nonumber \\ 10(x−2)(x−1) &= 0\nonumber \\ x &= 2\nonumber \\ x &= 1 \nonumber \end{align*}\]
Substituez les deux\(x\) valeurs dans l'équation linéaire d'origine à résoudre\(y\).
\[\begin{align*} y &= 3(2)−5\nonumber \\ &= 1\nonumber \\ y &= 3(1)−5\nonumber \\ &= −2 \nonumber \end{align*}\]
La droite coupe le cercle à\((2,1)\) et\((1,−2)\), ce qui peut être vérifié en substituant ces\((x,y)\) valeurs dans les deux équations d'origine (Figure\(\PageIndex{5}\)).
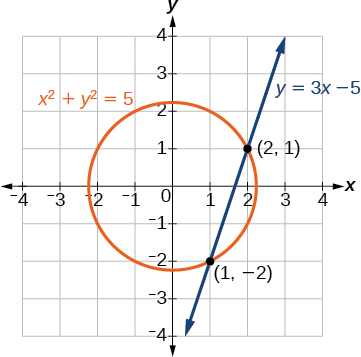
Figurine\(\PageIndex{5}\)
Résolvez le système d'équations non linéaires.
\[\begin{align*} x^2+y^2 &= 10\nonumber \\ x−3y &= −10 \nonumber \end{align*}\]
- Réponse
-
\((−1,3)\)
Résolution d'un système d'équations non linéaires par élimination
Nous avons vu que la substitution est souvent la méthode préférée lorsqu'un système d'équations comprend une équation linéaire et une équation non linéaire. Cependant, lorsque les deux équations du système ont des variables similaires du second degré, il est souvent plus facile de les résoudre par élimination par addition que par substitution. En général, l'élimination est une méthode beaucoup plus simple lorsque le système n'implique que deux équations à deux variables (un système deux par deux), plutôt qu'un système trois par trois, car il y a moins d'étapes. À titre d'exemple, nous étudierons les types de solutions possibles lors de la résolution d'un système d'équations représentant un cercle et une ellipse.
La figure\(\PageIndex{6}\) illustre des ensembles de solutions possibles pour un système d'équations impliquant un cercle et une ellipse.
- Aucune solution - Le cercle et l'ellipse ne se croisent pas. Une forme se trouve à l'intérieur de l'autre ou du cercle et l'ellipse se trouve à une certaine distance de l'autre.
- Une solution : le cercle et l'ellipse sont tangents l'un à l'autre et se croisent exactement en un point.
- Deux solutions : le cercle et l'ellipse se croisent en deux points.
- Trois solutions - Le cercle et l'ellipse se croisent en trois points.
- Quatre solutions - Le cercle et l'ellipse se croisent en quatre points.
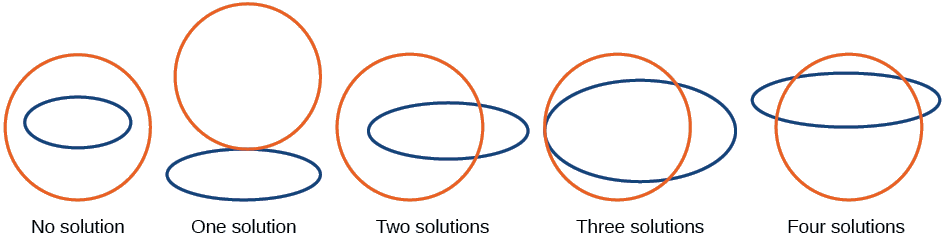
Figurine\(\PageIndex{6}\)
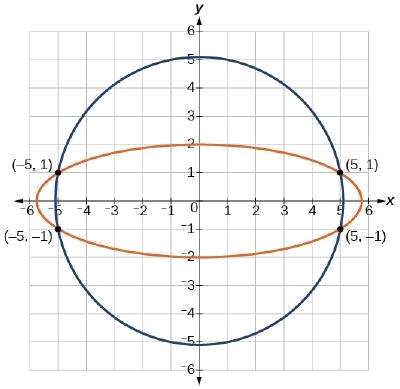
Résolvez le système d'équations non linéaires.
\[\begin{align*} x^2+y^2 &= 26 &(1)\nonumber \\ 3x^2+25y^2 &= 100 & (2) \nonumber \end{align*}\]
Solution
Commençons par multiplier l'équation (1) par\(−3\) et l'ajouter à l'équation (2).
\[\begin{align*} (−3)(x^2+y^2) = (−3)(26)&\nonumber \\ −3x^2−3y^2 = −78 &\nonumber \\ \underline{3x^2+25y^2=100}&\nonumber \\ 22y^2=22& \nonumber \end{align*}\]
Après avoir additionné les deux équations, nous résolvons pour\(y\).
\[\begin{align*} y^2 &= 1\nonumber \\ y &= \pm \sqrt{1}=\pm 1 \nonumber \end{align*}\]
Remplacez\(y=\pm 1\) par l'une des équations et résolvez pour\(x\).
\[\begin{align*} x^2+{(1)}^2 &= 26\nonumber \\ x^2+1 &= 26\nonumber \\ x^2 &= 25\nonumber \\ x &= \pm \sqrt{25}=\pm 5\nonumber \\ x^2+{(−1)}^2 &= 26\nonumber \\ x^2+1 &= 26\nonumber \\ x^2 &= \pm \sqrt{25}=\pm 5 \nonumber \end{align*}\]
Il existe quatre solutions :\((5,1)\)\((−5,1)\),\((5,−1)\), et\((−5,−1)\). Voir la figure\(\PageIndex{7}\).
Figurine\(\PageIndex{7}\)
Trouvez l'ensemble de solutions pour le système d'équations non linéaires donné.
\[\begin{align*} 4x^2+y^2 &= 13\nonumber \\ x^2+y^2 &= 10 \nonumber \end{align*}\]
- Réponse
-
\({(1,3),(1,−3),(−1,3),(−1,−3)}\)
Représentation graphique d'une inégalité non linéaire
Toutes les équations des systèmes que nous avons rencontrés jusqu'à présent impliquaient des égalités, mais nous pouvons également rencontrer des systèmes qui impliquent des inégalités. Nous avons déjà appris à représenter graphiquement les inégalités linéaires en traçant l'équation correspondante, puis en ombrant la région représentée par le symbole d'inégalité. Nous allons maintenant suivre des étapes similaires pour représenter graphiquement une inégalité non linéaire afin d'apprendre à résoudre des systèmes d'inégalités non linéaires. Une inégalité non linéaire est une inégalité contenant une expression non linéaire. Représenter graphiquement une inégalité non linéaire est similaire à la représentation graphique d'une inégalité linéaire.
N'oubliez pas que lorsque l'inégalité est supérieure ou inférieure à\(y<a\), le graphique est dessiné avec une ligne pointillée.\(y>a\) Lorsque l'inégalité est supérieure ou égale à\(y≥a\), ou inférieure ou égale à\(y≤a\), le graphique est dessiné avec une ligne continue. Les graphes créeront des régions dans le plan, et nous testerons chaque région pour trouver une solution. Si un point de la région fonctionne, c'est toute la région qui fonctionne. C'est la région que nous ombrageons (Figure\(\PageIndex{8}\)).
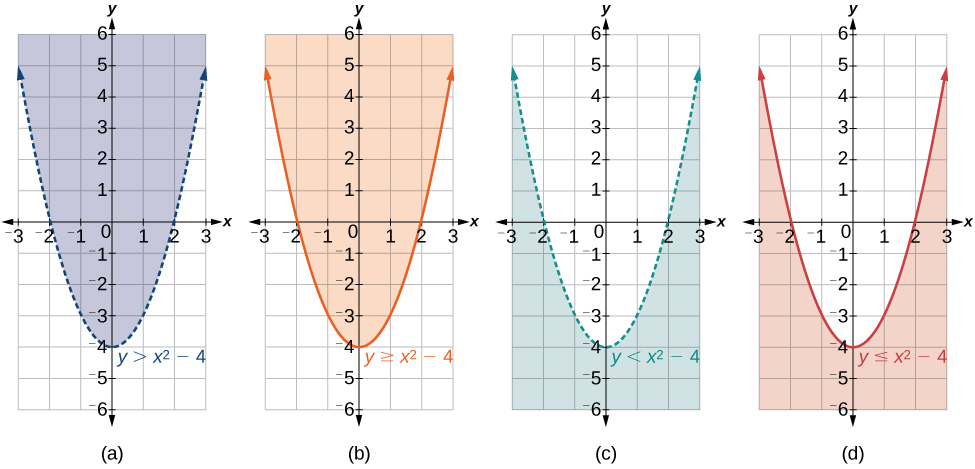
Figure\(\PageIndex{8}\) : (a) un exemple de\(y>a\) ; (b) un exemple de\(y≥a\) ; (c) un exemple de\(y<a\) ; (d) un exemple de\(y≤a\)
- Tracez la parabole comme s'il s'agissait d'une équation. Il s'agit de la limite de la région qui constitue l'ensemble de solutions.
- Si la limite est incluse dans la région (l'opérateur est\(≤\) ou\(≥\)), la parabole est représentée sous forme de ligne continue.
- Si la limite n'est pas incluse dans la région (l'opérateur est\(<\) ou\(>\)), la parabole est représentée sous forme de ligne pointillée.
- Testez un point dans l'une des régions pour déterminer s'il répond à la déclaration d'inégalité. Si l'énoncé est vrai, l'ensemble de solutions est la région incluant le point. Si l'instruction est fausse, l'ensemble de solutions est la région située de l'autre côté de la ligne de démarcation.
- Ombrez la région représentant l'ensemble de solutions.
Tracez l'inégalité\(y>x^2+1\).
Solution
Commencez par représenter graphiquement l'équation correspondante\(y=x^2+1\). Comme le symbole\(y>x^2+1\) est supérieur à, nous dessinons le graphique avec une ligne pointillée. Ensuite, nous choisissons les points à tester à l'intérieur et à l'extérieur de la parabole. Tester les points
\((0,2)\)et\((2,0)\). Un point se trouve clairement à l'intérieur de la parabole et l'autre est clairement à l'extérieur.
\[\begin{align*} y &> x^2+1\nonumber \\ 2 &> (0)^2+1\nonumber \\ 2 &>1 & \text{True}\nonumber \\\nonumber \\\nonumber \\ 0 &> (2)^2+1\nonumber \\ 0 &> 5 & \text{False} \nonumber \end{align*}\]
Le graphique est illustré dans la figure\(\PageIndex{9}\). Nous pouvons voir que l'ensemble de solutions comprend tous les points situés à l'intérieur de la parabole, mais pas sur le graphique lui-même.
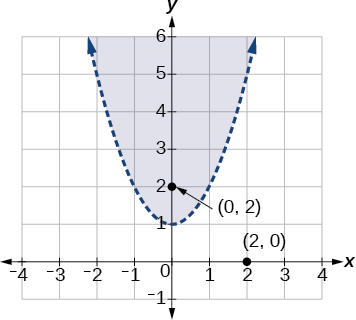
Figurine\(\PageIndex{9}\)
Représentation graphique d'un système d'inégalités non linéaires
Maintenant que nous avons appris à représenter graphiquement les inégalités non linéaires, nous pouvons apprendre à représenter graphiquement des systèmes d'inégalités non linéaires. Un système d'inégalités non linéaires est un système d'au moins deux inégalités dans deux variables ou plus contenant au moins une inégalité qui n'est pas linéaire. La représentation graphique d'un système d'inégalités non linéaires est similaire à la représentation graphique d'un système d'inégalités linéaires. La différence est que notre graphique peut donner lieu à un plus grand nombre de régions ombrées représentant une solution que dans un système d'inégalités linéaires. La solution à un système non linéaire d'inégalités est la région du graphe où les régions ombrées du graphe de chaque inégalité se chevauchent, ou où les régions se croisent, appelée région réalisable.
- Trouvez les points d'intersection en résolvant le système d'équations non linéaires correspondant.
- Tracez les équations non linéaires.
- Trouvez les régions ombrées de chaque inégalité.
- Identifiez la région réalisable comme étant l'intersection des régions ombrées de chaque inégalité ou l'ensemble des points communs à chaque inégalité.
Représentez graphiquement le système d'inégalités donné.
\[\begin{align*} x^2−y &≤ 0\nonumber \\ 2x^2+y &≤ 12 \nonumber \end{align*}\]
Solution
Ces deux équations sont clairement des paraboles. Nous pouvons trouver les points d'intersection par le processus d'élimination : ajoutez les deux équations et la variable\(y\) sera éliminée. Ensuite, nous résolvons pour\(x\).
\[\begin{align*} x^2−y = 0&\nonumber \\ \underline{2x^2+y=12}&\nonumber \\ 3x^2=12&\nonumber \\ x^2=4 &\nonumber \\ x=\pm 2 & \nonumber \end{align*}\]
Substituez les\(x\) valeurs -dans l'une des équations et résolvez pour\(y\).
\[\begin{align*} x^2−y &= 0\nonumber \\ {(2)}^2−y &= 0\nonumber \\ 4−y &= 0\nonumber \\ y &= 4\nonumber \\\nonumber \\ {(−2)}^2−y &= 0\nonumber \\ 4−y &= 0\nonumber \\ y &= 4 \nonumber \end{align*}\]
Les deux points d'intersection sont\((2,4)\) et\((−2,4)\). Notez que les équations peuvent être réécrites comme suit.
\[\begin{align*} x^2-y & ≤ 0\nonumber \\ x^2 &≤ y\nonumber \\ y &≥ x^2\nonumber \\\nonumber \\\nonumber \\ 2x^2+y &≤ 12\nonumber \\ y &≤ −2x^2+12 \nonumber \end{align*}\]
Tracez chaque inégalité. Voir la figure\(\PageIndex{10}\). La région réalisable est la région située entre les deux équations délimitées par\(2x^2+y≤12\) le haut et par\(x^2−y≤0\) le bas.
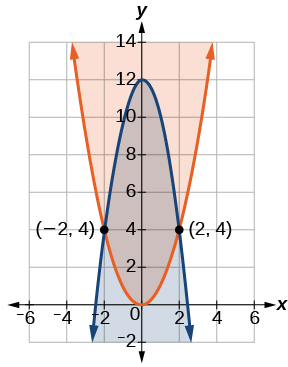
Figurine\(\PageIndex{10}\)
Représentez graphiquement le système d'inégalités donné.
\[\begin{align*} y &≥ x^2−1\nonumber \\ x−y &≥ −1 \nonumber \end{align*}\]
- Réponse
-
Ombrez la zone délimitée par les deux courbes, au-dessus du quadratique et en dessous de la ligne.
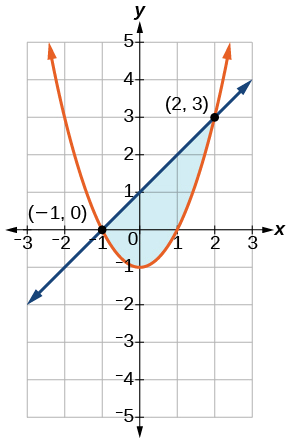
Figurine\(\PageIndex{11}\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les équations non linéaires.
Key Concepts
- There are three possible types of solutions to a system of equations representing a line and a parabola: (1) no solution, the line does not intersect the parabola; (2) one solution, the line is tangent to the parabola; and (3) two solutions, the line intersects the parabola in two points. See Example \(\PageIndex{1}\).
- There are three possible types of solutions to a system of equations representing a circle and a line: (1) no solution, the line does not intersect the circle; (2) one solution, the line is tangent to the parabola; (3) two solutions, the line intersects the circle in two points. See Example \(\PageIndex{2}\).
- There are five possible types of solutions to the system of nonlinear equations representing an ellipse and a circle:
(1) no solution, the circle and the ellipse do not intersect; (2) one solution, the circle and the ellipse are tangent to each other; (3) two solutions, the circle and the ellipse intersect in two points; (4) three solutions, the circle and ellipse intersect in three places; (5) four solutions, the circle and the ellipse intersect in four points. See Example \(\PageIndex{3}\). - An inequality is graphed in much the same way as an equation, except for > or <, we draw a dashed line and shade the region containing the solution set. See Example \(\PageIndex{4}\).
- Inequalities are solved the same way as equalities, but solutions to systems of inequalities must satisfy both inequalities. See Example \(\PageIndex{5}\).


