11.1 : Systèmes d'équations linéaires - Deux variables
- Page ID
- 195041
- Résolvez des systèmes d'équations en les graphiant.
- Résolvez des systèmes d'équations par substitution.
- Résolvez des systèmes d'équations par addition.
- Identifiez les systèmes d'équations incohérents contenant deux variables.
- Exprime la solution d'un système d'équations dépendantes contenant deux variables.
Un fabricant de planches à roulettes présente une nouvelle gamme de planches. Le fabricant suit ses coûts, c'est-à-dire le montant qu'il dépense pour produire les planches, et ses revenus, c'est-à-dire le montant qu'il gagne grâce à la vente de ses planches. Comment l'entreprise peut-elle déterminer si elle réalise des bénéfices avec sa nouvelle gamme ? Combien de planches à roulettes doivent être produites et vendues avant qu'un profit ne soit possible ? Dans cette section, nous examinerons des équations linéaires à deux variables pour répondre à ces questions et à des questions similaires.

Introduction aux systèmes d'équations
Afin d'étudier des situations telles que celle du fabricant de planches à roulettes, nous devons reconnaître que nous avons affaire à plus d'une variable et probablement à plus d'une équation. Un système d'équations linéaires se compose de deux équations linéaires ou plus composées de deux variables ou plus, de telle sorte que toutes les équations du système sont considérées simultanément. Pour trouver la solution unique à un système d'équations linéaires, nous devons trouver une valeur numérique pour chaque variable du système qui satisfera toutes les équations du système en même temps. Certains systèmes linéaires peuvent ne pas avoir de solution et d'autres peuvent avoir un nombre infini de solutions. Pour qu'un système linéaire ait une solution unique, il doit y avoir au moins autant d'équations que de variables. Toutefois, cela ne garantit pas une solution unique.
Dans cette section, nous allons examiner des systèmes d'équations linéaires à deux variables, qui consistent en deux équations contenant deux variables différentes. Par exemple, considérez le système d'équations linéaires à deux variables suivant.
\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]
La solution d'un système d'équations linéaires à deux variables est une paire ordonnée qui satisfait chaque équation indépendamment. Dans cet exemple, la paire ordonnée\((4,7)\) est la solution du système d'équations linéaires. Nous pouvons vérifier la solution en substituant les valeurs dans chaque équation pour voir si la paire ordonnée satisfait les deux équations. Nous étudierons prochainement les méthodes permettant de trouver une telle solution, si elle existe.
\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*}\]
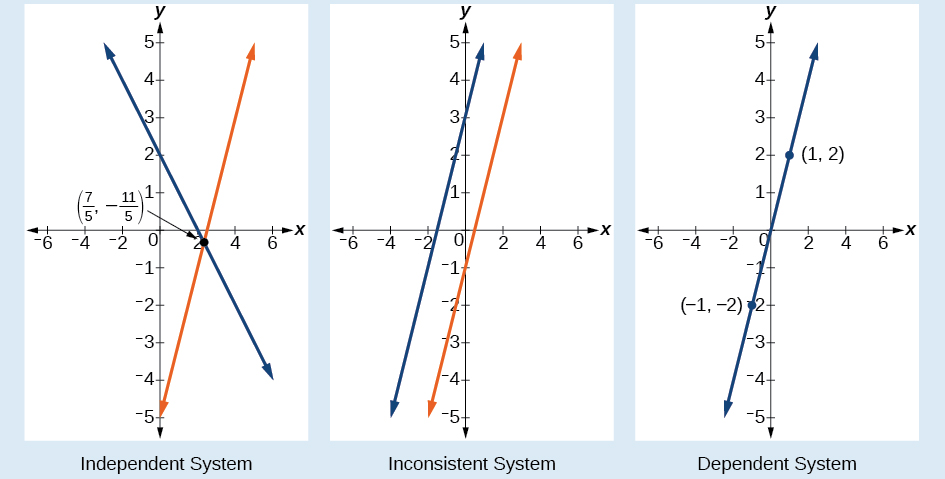
En plus de prendre en compte le nombre d'équations et de variables, nous pouvons classer les systèmes d'équations linéaires en fonction du nombre de solutions. Un système d'équations cohérent possède au moins une solution. Un système cohérent est considéré comme un système indépendant s'il possède une solution unique, comme dans l'exemple que nous venons d'explorer. Les deux lignes ont des pentes différentes et se croisent en un point du plan. Un système cohérent est considéré comme un système dépendant si les équations ont la même pente et les mêmes interceptions y. En d'autres termes, les lignes coïncident, de sorte que les équations représentent la même droite. Chaque point de la ligne représente une paire de coordonnées qui satisfait le système. Il existe donc une infinité de solutions.
Un autre type de système d'équations linéaires est un système incohérent, c'est-à-dire un système dans lequel les équations représentent deux droites parallèles. Les lignes ont la même pente et des intersections y- différentes. Il n'y a pas de points communs aux deux lignes ; il n'y a donc pas de solution au système.
Il existe trois types de systèmes d'équations linéaires à deux variables et trois types de solutions.
- Un système indépendant possède exactement une paire de solutions\((x,y)\). Le point où les deux lignes se croisent est la seule solution.
- Un système incohérent n'a pas de solution. Notez que les deux lignes sont parallèles et ne se croisent jamais.
- Un système dépendant a une infinité de solutions. Les lignes coïncident. Comme il s'agit de la même ligne, chaque paire de coordonnées sur la ligne est une solution aux deux équations.
La figure\(\PageIndex{2}\) compare les représentations graphiques de chaque type de système.
- Substituez la paire ordonnée dans chaque équation du système.
- Déterminez si les déclarations vraies résultent de la substitution dans les deux équations ; si tel est le cas, la paire ordonnée est une solution.
Déterminez si la paire ordonnée\((5,1)\) est une solution au système d'équations donné.
\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]
Solution
Substituez la paire ordonnée\((5,1)\) dans les deux équations.
\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{ True} \end{align*}\]
La paire ordonnée\((5,1)\) satisfait les deux équations, elle constitue donc la solution du système.
Analyse
Nous pouvons voir clairement la solution en traçant le graphique de chaque équation. Puisque la solution est une paire ordonnée qui satisfait aux deux équations, il s'agit d'un point sur les deux droites et donc du point d'intersection des deux droites. Voir la figure\(\PageIndex{3}\).
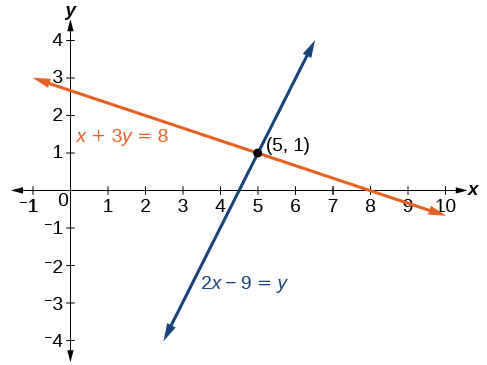
Déterminez si la paire ordonnée\((8,5)\) est une solution pour le système suivant.
\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]
- Réponse
-
Ce n'est pas une solution.
Résolution de systèmes d'équations par représentation graphique
Il existe plusieurs méthodes pour résoudre des systèmes d'équations linéaires. Pour un système d'équations linéaires à deux variables, nous pouvons déterminer à la fois le type de système et la solution en traçant le système d'équations sur le même ensemble d'axes.
Résolvez le système d'équations suivant en traçant un graphique. Identifiez le type de système.
\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]
Solution
Résolvez la première équation pour\(y\).
\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]
Résolvez la deuxième équation pour\(y\).
\[\begin{align*} x−y &= −1 \\ y &= x+1 \end{align*}\]
Représentez les deux équations sur le même ensemble d'axes comme dans la figure\(\PageIndex{4}\).
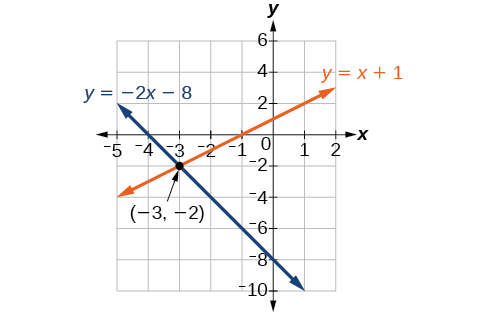
Les lignes semblent se croiser au point\((−3,−2)\). Nous pouvons vérifier qu'il s'agit de la solution du système en substituant la paire ordonnée dans les deux équations.
\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 &= −8 \text{ True} \\ (−3)−(−2) &= −1 \\ −1 &= −1 \text{ True} \end{align*}\]
La solution du système est la paire ordonnée\((−3,−2)\), de sorte que le système est indépendant.
Résolvez le système d'équations suivant en traçant un graphique.
\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]
- Réponse
-
La solution du système est la paire ordonnée\((−5,3)\).
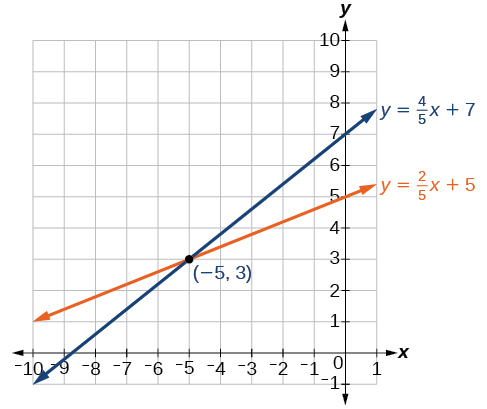
Figurine\(\PageIndex{5}\)
Le graphisme peut-il être utilisé si le système est incohérent ou dépendant ?
Oui, dans les deux cas, nous pouvons toujours représenter graphiquement le système pour déterminer le type de système et de solution. Si les deux lignes sont parallèles, le système n'a pas de solution et est incohérent. Si les deux lignes sont identiques, le système possède une infinité de solutions et est un système dépendant.
Résolution de systèmes d'équations par substitution
La résolution graphique d'un système linéaire à deux variables fonctionne bien lorsque la solution est composée de valeurs entières, mais si notre solution contient des décimales ou des fractions, ce n'est pas la méthode la plus précise. Nous examinerons deux autres méthodes pour résoudre un système d'équations linéaires plus précises que la représentation graphique. L'une de ces méthodes consiste à résoudre un système d'équations par la méthode de substitution, dans laquelle nous résolvons l'une des équations pour une variable, puis nous substituons le résultat dans la deuxième équation pour résoudre la deuxième variable. N'oubliez pas que nous ne pouvons résoudre qu'une seule variable à la fois, raison pour laquelle la méthode de substitution est à la fois utile et pratique.
- Résolvez l'une des deux équations pour l'une des variables en fonction de l'autre.
- Substituez l'expression de cette variable dans la deuxième équation, puis résolvez pour la variable restante.
- Substituez cette solution dans l'une ou l'autre des équations d'origine pour trouver la valeur de la première variable. Si possible, écrivez la solution sous forme de paire ordonnée.
- Vérifiez la solution dans les deux équations.
Résolvez le système d'équations suivant par substitution.
\[\begin{align*} −x+y &= −5 \\ 2x−5y &= 1 \end{align*}\]
Solution
Tout d'abord, nous allons résoudre la première équation pour\(y\).
\[\begin{align*} −x+y &=−5 \\ y &= x−5 \end{align*}\]
Nous pouvons maintenant remplacer l'expression\(x−5\) par\(y\) dans la deuxième équation.
\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x &= 8 \end{align*}\]
Maintenant, nous la\(x=8\) remplaçons dans la première équation et résolvons pour\(y\).
\[\begin{align*} −(8)+y &= −5 \\ y &= 3 \end{align*}\]
Notre solution est\((8,3)\).
Vérifiez la solution en la substituant\((8,3)\) dans les deux équations.
\[\begin{align*} −x+y &= −5 \\ −(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8)−5(3) &= 1 \text{ True} \end{align*}\]
Résolvez le système d'équations suivant par substitution.
\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]
- Réponse
-
\((−2,−5)\)
La méthode de substitution peut-elle être utilisée pour résoudre un système linéaire à deux variables ?
Oui, mais la méthode fonctionne mieux si l'une des équations contient un coefficient égal\(1\) ou égal à\(–1\) ce que nous n'ayons pas à traiter avec des fractions.
Résolution de systèmes d'équations à deux variables par la méthode d'addition
Une troisième méthode de résolution de systèmes d'équations linéaires est la méthode d'addition. Dans cette méthode, nous ajoutons deux termes avec la même variable, mais des coefficients opposés, de sorte que la somme soit nulle. Bien entendu, tous les systèmes ne sont pas configurés avec les deux termes d'une variable ayant des coefficients opposés. Nous devons souvent ajuster l'une des équations ou les deux par multiplication afin d'éliminer une variable par addition.
- Écrivez les deux équations avec des variables x et y sur le côté gauche du signe égal et des constantes sur la droite.
- Écrivez une équation au-dessus de l'autre en alignant les variables correspondantes. Si l'une des variables de l'équation supérieure possède le coefficient opposé à celui de la même variable de l'équation inférieure, additionnez les équations ensemble en éliminant une variable. Sinon, multipliez par un nombre différent de zéro afin que l'une des variables de l'équation supérieure ait le coefficient opposé à celui de la même variable dans l'équation inférieure, puis ajoutez les équations pour éliminer la variable.
- Résolvez l'équation résultante pour la variable restante.
- Substituez cette valeur dans l'une des équations d'origine et résolvez pour la deuxième variable.
- Vérifiez la solution en substituant les valeurs dans l'autre équation.
Résolvez le système d'équations donné par addition.
\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]
Solution
Les deux équations sont déjà définies comme étant égales à une constante. Notez que le coefficient de\(x\) dans la deuxième équation\(–1\),, est l'opposé du coefficient\(x\) de la première équation,\(1\). Nous pouvons ajouter les deux équations à éliminer\(x\) sans avoir à les multiplier par une constante.
\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]
Maintenant que nous avons éliminé\(x\), nous pouvons résoudre l'équation résultante pour\(y\).
\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]
Ensuite, nous remplaçons cette valeur\(y\) dans l'une des équations d'origine et résolvons pour\(x\).
\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ −x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]
La solution à ce système est\(\left(−\dfrac{7}{3},\dfrac{2}{3}\right)\).
Vérifiez la solution dans la première équation.
\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) &= \\ −\dfrac{7}{3}+\dfrac{4}{3} &= −\dfrac{3}{3} \\ −1 &= −1 \;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Analyse
Nous obtenons une perspective importante sur les systèmes d'équations en examinant la représentation graphique. Voir la figure\(\PageIndex{6}\) pour déterminer si les équations se croisent au niveau de la solution. Il n'est pas nécessaire de se demander s'il existe une deuxième solution, car l'observation du graphique confirme que le système possède exactement une solution.
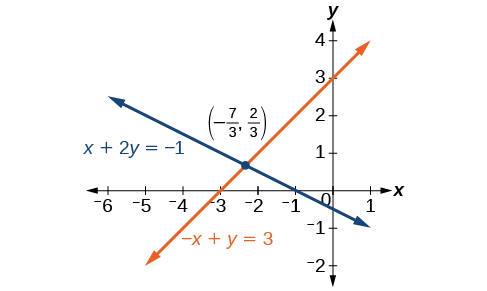
Résolvez le système d'équations donné par la méthode d'addition.
\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]
Solution
L'ajout de ces équations telles que présentées n'éliminera aucune variable. Cependant, nous voyons que la première équation contient et que la seconde\(3x\) en contient\(x\). Donc, si nous multiplions la deuxième équation par\(−3\), les termes x s'additionneront à zéro.
\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Multiply both sides by }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Use the distributive property.} \end{align*}\]
Maintenant, ajoutons-les.
\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{align*}\]
Pour la dernière étape, nous la remplaçons\(y=−4\) dans l'une des équations d'origine et résolvons pour\(x\).
\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \end{align*}\]
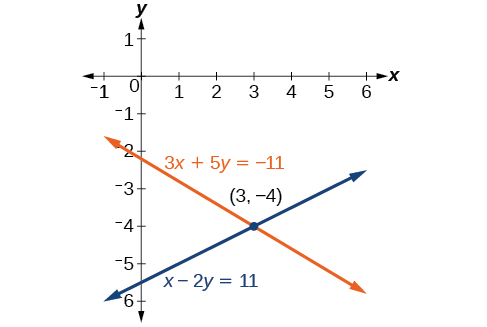
Notre solution est la paire commandée\((3,−4)\). Voir la figure\(\PageIndex{7}\). Vérifiez la solution dans la deuxième équation d'origine.
\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Résolvez le système d'équations par addition.
\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]
- Réponse
-
\((−6,−2)\)
Résolvez le système d'équations donné en deux variables par addition.
\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]
Solution
Une équation l'a fait\(2x\) et l'autre l'a fait\(5x\). Le multiple le moins courant est\(10x\) que nous devrons multiplier les deux équations par une constante afin d'éliminer une variable. Éliminons\(x\) en multipliant la première équation par\(−5\) et la deuxième équation par\(2\).
\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x−20y &= 60 \end{align*}\]
Ensuite, nous additionnons les deux équations.
\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align*}\]
Remplacer\(y=−4\) dans la première équation d'origine.
\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*}\]
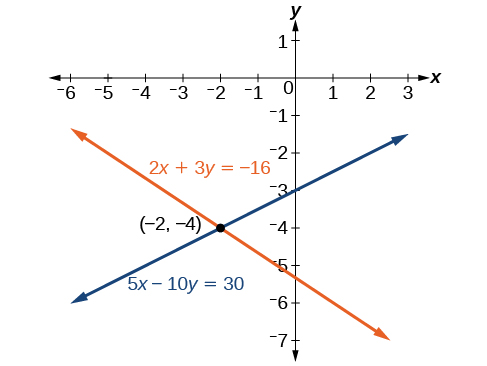
La solution est\((−2,−4)\). Vérifiez-le dans l'autre équation.
\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{align*}\]
Voir la figure\(\PageIndex{8}\).
Résolvez le système d'équations donné en deux variables par addition.
\[ \begin{align*} \dfrac{x}{3}+\dfrac{y}{6} &= 3 \\ \dfrac{x}{2}−\dfrac{y}{4} &= 1 \end{align*}\]
Solution
Commencez par effacer chaque équation des fractions en multipliant les deux côtés de l'équation par le plus petit dénominateur commun.
\[\begin{align*} 6\left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= 6(3) \\ 2x+y &= 18 \\ 4\left(\dfrac{x}{2}−\dfrac{y}{4}\right) &= 4(1) \\ 2x−y &= 4 \end{align*}\]
Multipliez maintenant la deuxième équation par\(−1\) afin d'éliminer la variable x.
\[\begin{align*} −1(2x−y) &= −1(4) \\ −2x+y &= −4 \end{align*}\]
Ajoutez les deux équations pour éliminer la\(x\) variable -et résoudre l'équation résultante.
\[\begin{align*} 2x+y &= 18 \\ −2x+y &= −4 \\ 2y &= 14 \\ y &=7 \end{align*}\]
Substituer\(y=7\) dans la première équation.
\[\begin{align*} 2x+(7) &= 18 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \\ &= 7.5 \end{align*}\]
La solution est\(\left(\dfrac{11}{2},7\right)\). Vérifiez-le dans l'autre équation.
\[\begin{align*} \dfrac{x}{2}−\dfrac{y}{4} &= 1 \\ \dfrac{\dfrac{11}{2}}{2}−\dfrac{7}{4} &=1 \\ \dfrac{11}{4}−\dfrac{7}{4} &=1 \\ \dfrac{4}{4} &=1 \end{align*}\]
Résolvez le système d'équations par addition.
\[\begin{align*} 2x+3y &= 8 \\ 3x+5y &= 10 \end{align*}\]
- Réponse
-
\((10,−4)\)
Identification de systèmes d'équations incohérents contenant deux variables
Maintenant que nous disposons de plusieurs méthodes pour résoudre des systèmes d'équations, nous pouvons les utiliser pour identifier les systèmes incohérents. Rappelez-vous qu'un système incohérent est constitué de lignes parallèles qui ont la même pente mais des intersections Y différentes. Ils ne se croiseront jamais. Lorsque vous recherchez une solution à un système incohérent, nous trouverons une fausse déclaration, telle que\(12=0\).
Résolvez le système d'équations suivant.
\[\begin{align*} x &= 9−2y \\ x+2y &= 13 \end{align*}\]
Solution
Nous pouvons aborder ce problème de deux manières. Comme une équation est déjà résolue\(x\), l'étape la plus évidente consiste à utiliser la substitution.
\[\begin{align*} x+2y &= 13 \\ (9−2y)+2y &= 13 \\ 9+0y &= 13 \\ 9 &= 13 \end{align*}\]
De toute évidence, cette déclaration est contradictoire car\(9≠13\). Le système n'a donc pas de solution.
La deuxième approche consisterait à manipuler d'abord les équations de manière à ce qu'elles soient toutes deux sous forme d'intersection de pente. Nous manipulons la première équation comme suit.
\[\begin{align*} x &= 9−2y \\ 2y &= −x+9 \\ y &= −\dfrac{1}{2}x+\dfrac{9}{2} \end{align*}\]
Nous convertissons ensuite la deuxième équation exprimée sous forme d'intersection de pente.
\[\begin{align*} x+2y &= 13 \\ 2y &= −x+13 \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
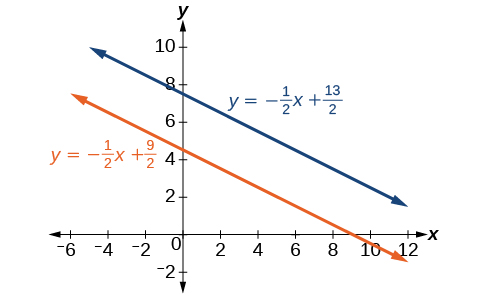
En comparant les équations, nous voyons qu'elles ont la même pente mais\(y\) des interceptions différentes. Les lignes sont donc parallèles et ne se croisent pas.
\[\begin{align*} y &= −\dfrac{1}{2}x+\dfrac{9}{2} \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Analyse
L'écriture des équations sous forme d'intersection de pente confirme que le système est incohérent car toutes les lignes finiront par se croiser à moins qu'elles ne soient parallèles. Les lignes parallèles ne se croisent jamais ; les deux lignes n'ont donc aucun point commun. Les graphes des équations de cet exemple sont illustrés dans la figure\(\PageIndex{9}\).
Résolvez le système d'équations suivant en deux variables.
\[\begin{align*} 2y−2x &= 2 \\ 2y−2x &= 6 \end{align*}\]
- Réponse
-
Aucune solution. Il s'agit d'un système incohérent.
Exprimer la solution d'un système d'équations dépendantes contenant deux variables
Rappelons qu'un système dépendant d'équations à deux variables est un système dans lequel les deux équations représentent la même droite. Les systèmes dépendants ont un nombre infini de solutions, car tous les points d'une ligne se trouvent également sur l'autre ligne. Après avoir utilisé la substitution ou l'addition, l'équation résultante sera une identité, telle que\(0=0\).
Trouvez une solution au système d'équations à l'aide de la méthode d'addition.
\[\begin{align*} x+3y &= 2 \\ 3x+9y &= 6 \end{align*}\]
Solution
Avec la méthode d'addition, nous voulons éliminer l'une des variables en ajoutant les équations. Dans ce cas, concentrons-nous sur l'élimination\(x\). Si nous multiplions les deux côtés de la première équation par\(−3\), nous serons alors en mesure d'éliminer la variable x.
\[\begin{align*} x+3y &= 2 \\ (−3)(x+3y) &= (−3)(2) \\ −3x−9y &= −6 \end{align*}\]
Ajoutez maintenant les équations.
\[\begin{align*} -3x-9y &= -6 \\ \underline{+\space 3x+9y}& = \underline{6} \\ 0&= 0 \\ \end{align*}\]
Nous pouvons voir qu'il y aura une infinité de solutions qui satisferont les deux équations.
Analyse
Si nous réécrivions les deux équations sous la forme de l'intersection de pente, nous saurons peut-être à quoi ressemblerait la solution avant de les ajouter. Regardons ce qui se passe lorsque nous convertissons le système en forme d'interception en pente.
\[ \begin{align*} x+3y &= 2 \\ 3y &= −x+2 \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \\ 3x+9y &= 6 \\ 9y &=−3x+6 \\ y &= −\dfrac{3}{9}x+\dfrac{6}{9} \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \end{align*}\]
Voir la figure\(\PageIndex{10}\). Remarquez que les résultats sont les mêmes. La solution générale du système est\(\left(x, −\dfrac{1}{3}x+\dfrac{2}{3}\right)\).
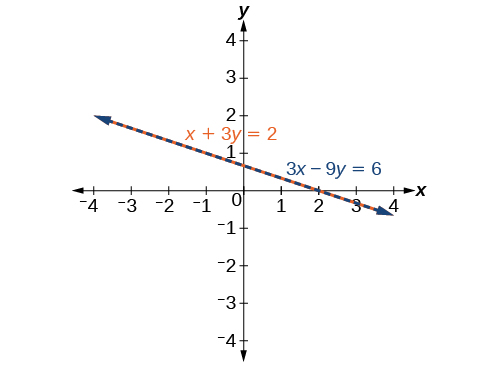
Résolvez le système d'équations suivant en deux variables.
\[\begin{align*} y−2x &= 5 \\ −3y+6x &= −15 \end{align*}\]
- Réponse
-
Le système étant dépendant, il existe une infinité de solutions du formulaire\((x,2x+5)\).
Utiliser des systèmes d'équations pour étudier les profits
En utilisant ce que nous avons appris sur les systèmes d'équations, nous pouvons revenir au problème de fabrication du skateboard au début de la section. La fonction de chiffre d'affaires du fabricant de planches à roulettes est la fonction utilisée pour calculer le montant d'argent investi dans l'entreprise. Il peut être représenté par l'équation\(R=xp\), où\(x\) =quantité et\(p\) =prix. La fonction de recettes est indiquée en orange sur la figure\(\PageIndex{11}\).
La fonction de coût est la fonction utilisée pour calculer les coûts liés à l'exercice d'une activité. Cela inclut les coûts fixes, tels que les loyers et les salaires, et les coûts variables, tels que les services publics. La fonction de coût est illustrée en bleu sur la figure\(\PageIndex{11}\). L'\(x\)axe -représente la quantité en centaines d'unités. L'\(y\)axe -représente les coûts ou les recettes en centaines de dollars.
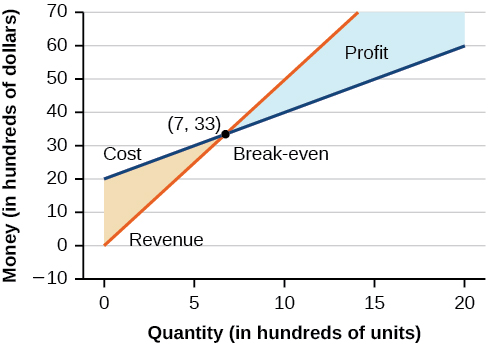
Le point auquel les deux lignes se croisent est appelé point d'équilibre. Nous pouvons voir sur le graphique que si\(700\) des unités sont produites, le coût l'est\($3,300\) et les recettes également\($3,300\). En d'autres termes, l'entreprise atteint le seuil de rentabilité si elle produit et vend des\(700\) unités. Ils ne gagnent ni ne perdent d'argent.
La zone ombrée à droite du seuil de rentabilité représente les quantités pour lesquelles l'entreprise réalise des bénéfices. La zone ombrée à gauche représente les quantités pour lesquelles l'entreprise subit une perte. La fonction de profit est la fonction de recettes moins la fonction de coût, exprimée sous la forme\(P(x)=R(x)−C(x)\). De toute évidence, il est très important pour les entreprises de connaître la quantité pour laquelle le coût est égal aux recettes.
Compte tenu de la fonction de coût\(C(x)=0.85x+35,000\) et de la fonction de recettes\(R(x)=1.55x\), déterminez le seuil de rentabilité et la fonction de profit.
Solution
Écrivez le système d'équations en utilisant\(y\) pour remplacer la notation des fonctions.
\[\begin{align*} y &= 0.85x+35,000 \\ y &= 1.55x \end{align*}\]
Remplacez l'expression\(0.85x+35,000\) de la première équation par la deuxième équation et résolvez pour\(x\).
\[\begin{align*} 0.85x+35,000 &= 1.55x \\ 35,000 &= 0.7x \\ 50,000 &= x \end{align*}\]
Ensuite, nous la\(x=50,000\) substituons à la fonction de coût ou à la fonction de recettes.
\(1.55(50,000)=77,500\)
Le seuil de rentabilité est\((50,000,77,500)\).
La fonction de profit est déterminée à l'aide de la formule\(P(x)=R(x)−C(x)\).
\[\begin{align*} P(x) &= 1.55x−(0.85x+35,000) \\ &=0.7x−35,000 \end{align*}\]
La fonction de profit est\(P(x)=0.7x−35,000\).
Analyse
Le coût de production des\(50,000\) unités est de\($77,500\), et les recettes provenant de la vente d'\(50,000\)unités l'sont également\($77,500\). Pour réaliser des bénéfices, l'entreprise doit produire et vendre plus que\(50,000\) des unités. Voir la figure\(\PageIndex{12}\).
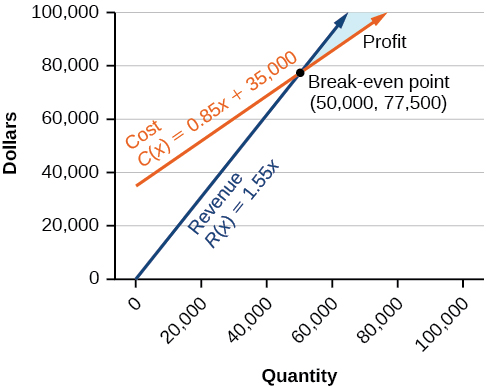
Nous voyons sur le graphique de la figure\(\PageIndex{13}\) que la fonction de profit a une valeur négative jusqu'à ce que\(x=50,000\) le graphique croise l'\(x\)axe des. Ensuite, le graphique apparaît sous forme de\(y\) valeurs positives et continue sur cette trajectoire car la fonction de profit est une ligne droite. Cela montre que le seuil de rentabilité pour les entreprises se situe lorsque la fonction de profit est\(0\). La zone située à gauche du seuil de rentabilité représente un fonctionnement à perte.
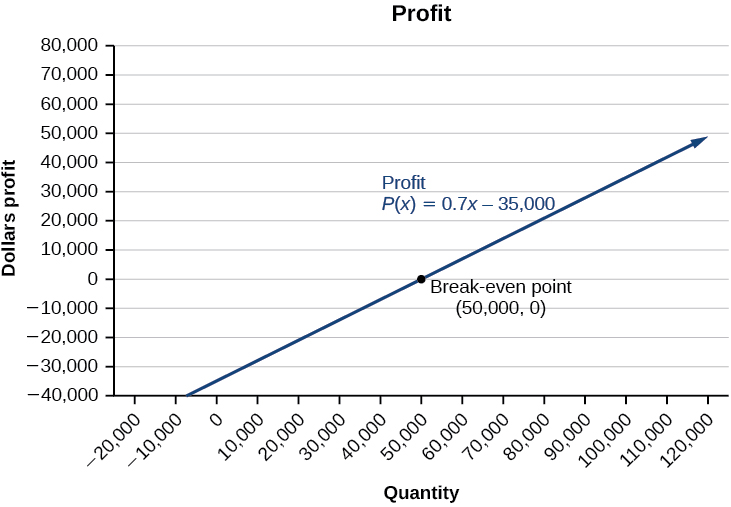
Le prix d'un billet pour le cirque est\($25.00\) pour les enfants et\($50.00\) pour les adultes. Un certain jour, la fréquentation du cirque est\(2,000\) et le total des recettes d'entrée est de\($70,000\). Combien d'enfants et combien d'adultes ont acheté des billets ?
Solution
Soit\(c\) le nombre d'enfants et\(a\) = le nombre d'adultes présents.
Le nombre total de personnes est de\(2,000\). Nous pouvons l'utiliser pour écrire une équation du nombre de personnes présentes au cirque ce jour-là.
\(c+a=2,000\)
Les revenus de tous les enfants peuvent être obtenus en multipliant\($25.00\) par le nombre d'enfants\(25c\). Les revenus de tous les adultes peuvent être obtenus en multipliant\($50.00\) par le nombre d'adultes,\(50a\). Le chiffre d'affaires total est de\($70,000\). Nous pouvons l'utiliser pour écrire une équation pour les recettes.
\(25c+50a=70,000\)
Nous avons maintenant un système d'équations linéaires à deux variables.
\(c+a=2,000\)
\(25c+50a=70,000\)
Dans la première équation, le coefficient des deux variables est\(1\). Nous pouvons résoudre rapidement la première équation pour l'un\(c\) ou l'autre\(a\). Nous allons résoudre pour\(a\).
\[\begin{align*} c+a &= 2,000 \\ a &= 2,000−c \end{align*}\]
Remplacez l'expression\(2,000−c\) de la deuxième équation par a et résolvez par\(c\).
\[\begin{align*} 25c+50(2,000−c) &= 70,000 \\ 25c+100,000−50c &= 70,000 \\ −25c &= −30,000 \\ c &= 1,200 \end{align*}\]
Substituez\(c=1,200\) dans la première équation à résoudre\(a\).
\[\begin{align*} 1,200+a &= 2,000 \\ a &= 800 \end{align*}\]
Nous constatons que des\(1,200\) enfants et des\(800\) adultes ont acheté des billets pour le cirque ce jour-là.
Les billets de repas au cirque coûtent\($4.00\) pour les enfants et\($12.00\) pour les adultes. Si des tickets de\(1,650\) repas ont été achetés pour un total de\($14,200\), combien d'enfants et combien d'adultes ont acheté des tickets de repas ?
- Réponse
-
\(700\)enfants,\(950\) adultes
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les systèmes d'équations linéaires.
Concepts clés
- Un système d'équations linéaires se compose de deux équations ou plus composées de deux variables ou plus, de telle sorte que toutes les équations du système sont considérées simultanément.
- La solution d'un système d'équations linéaires à deux variables est une paire ordonnée qui satisfait chaque équation indépendamment. Voir l'exemple\(\PageIndex{1}\).
- Les systèmes d'équations sont classés comme indépendants avec une solution, dépendants d'un nombre infini de solutions ou incompatibles avec l'absence de solution.
- L'une des méthodes permettant de résoudre un système d'équations linéaires à deux variables consiste à représenter graphiquement. Dans cette méthode, nous tracons les équations sur le même ensemble d'axes. Voir l'exemple\(\PageIndex{2}\).
- Une autre méthode de résolution d'un système d'équations linéaires est la substitution. Dans cette méthode, nous résolvons une variable dans une équation et substituons le résultat dans la deuxième équation. Voir l'exemple\(\PageIndex{3}\).
- Une troisième méthode pour résoudre un système d'équations linéaires est l'addition, dans laquelle nous pouvons éliminer une variable en ajoutant des coefficients opposés aux variables correspondantes. Voir l'exemple\(\PageIndex{4}\).
- Il est souvent nécessaire de multiplier l'une ou les deux équations par une constante pour faciliter l'élimination d'une variable lors de l'addition des deux équations. Voir Exemple\(\PageIndex{5}\)\(\PageIndex{6}\), Exemple et Exemple\(\PageIndex{7}\).
- L'une ou l'autre méthode de résolution d'un système d'équations aboutit à une fausse déclaration pour les systèmes incohérents, car ils sont constitués de lignes parallèles qui ne se croisent jamais. Voir l'exemple\(\PageIndex{8}\).
- La solution à un système d'équations dépendantes sera toujours vraie, car les deux équations décrivent la même droite. Voir l'exemple\(\PageIndex{9}\).
- Des systèmes d'équations peuvent être utilisés pour résoudre des problèmes du monde réel impliquant plusieurs variables, tels que ceux liés aux recettes, aux coûts et aux bénéfices. Voir Exemple\(\PageIndex{10}\) et Exemple\(\PageIndex{11}\).


