8.1 : Graphiques des fonctions sinusoïdale et cosinusoïdale
- Page ID
- 195232
- Graphiques des variations de\(y=\sin( x )\) et\(y=\cos( x )\).
- Utilisez les déphasages des courbes sinusoïdales et cosinus.
La lumière blanche, telle que la lumière du soleil, n'est pas du tout blanche. Il s'agit plutôt d'une composition de toutes les couleurs de l'arc-en-ciel sous forme de vagues. Les couleurs individuelles ne sont visibles que lorsque la lumière blanche passe à travers un prisme optique qui sépare les ondes en fonction de leurs longueurs d'onde pour former un arc-en-ciel.

Les ondes lumineuses peuvent être représentées graphiquement par la fonction sinusoïdale. Dans le chapitre sur les fonctions trigonométriques, nous avons examiné les fonctions trigonométriques telles que la fonction sinusoïdale. Dans cette section, nous allons interpréter et créer des graphes des fonctions sinusoïdales et cosinusoïdales.
Représentation graphique des fonctions sinus et cosinus
Rappelez-vous que les fonctions sinus et cosinus associent les valeurs réelles aux\(y\) coordonnées\(x\) - et - d'un point du cercle unitaire. Alors, à quoi ressemblent-ils sur un graphique sur un plan de coordonnées ? Commençons par la fonction sinusoïdale. Nous pouvons créer un tableau de valeurs et les utiliser pour esquisser un graphique. Le tableau\(\PageIndex{1}\) répertorie certaines des valeurs de la fonction sinus sur un cercle unitaire.
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\sin(x)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) |
Le fait de tracer les points du tableau et de continuer le long de l'axe x donne la forme de la fonction sinusoïdale. Voir la figure\(\PageIndex{2}\).
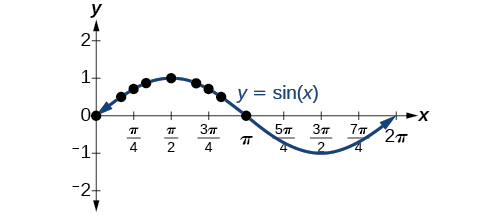
Remarquez que les valeurs des sinus sont positives entre\(0\) et\(\pi\), qui correspondent aux valeurs de la fonction sinus dans les quadrants I et II du cercle unitaire, et que les valeurs des sinus sont négatives entre\(\pi\) et\(2\pi\), qui correspondent aux valeurs de la fonction sinus dans les quadrants III et IV sur le cercle de l'unité. Voir la figure\(\PageIndex{3}\).
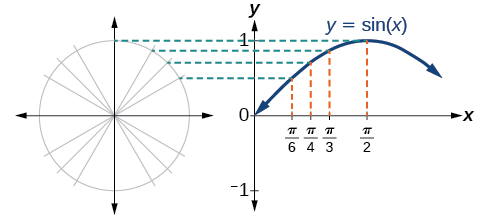
Examinons maintenant de la même manière la fonction cosinus. Encore une fois, nous pouvons créer un tableau de valeurs et les utiliser pour esquisser un graphique. Le tableau\(\PageIndex{2}\) répertorie certaines des valeurs de la fonction cosinus sur un cercle unitaire.
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\cos(x)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) | \(-\dfrac{1}{2}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-1\) |
Comme pour la fonction sinusoïdale, nous pouvons tracer des points pour créer un graphique de la fonction cosinus comme dans la figure\(\PageIndex{4}\).
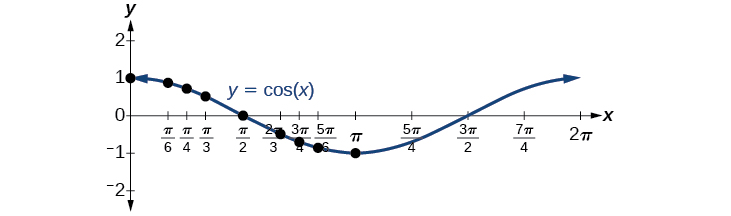
Comme nous pouvons évaluer le sinus et le cosinus de n'importe quel nombre réel, ces deux fonctions sont définies pour tous les nombres réels. En considérant les valeurs du sinus et du cosinus comme des coordonnées de points sur un cercle unitaire, il devient clair que la plage des deux fonctions doit être l'intervalle\([ −1,1 ]\).
Dans les deux graphes, la forme du graphique se répète après\(2\pi\), ce qui signifie que les fonctions sont périodiques avec une période de\(2\pi\). Une fonction périodique est une fonction pour laquelle un décalage horizontal spécifique\(P\) aboutit à une fonction égale à la fonction d'origine :\(f(x+P)=f(x)\) pour toutes les valeurs du\(x\) domaine de\(f\). Lorsque cela se produit, nous appelons le plus petit décalage horizontal de ce type avec\(P>0\) la période de la fonction. La figure\(\PageIndex{5}\) montre plusieurs périodes des fonctions sinus et cosinus.
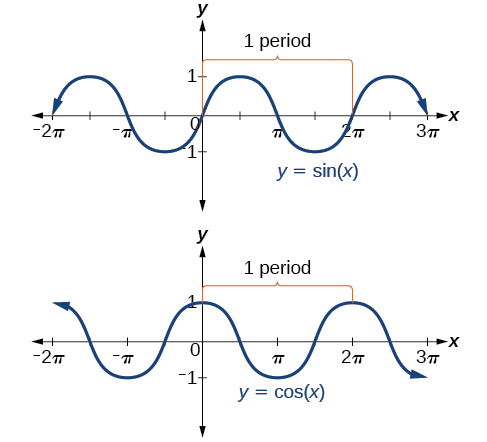
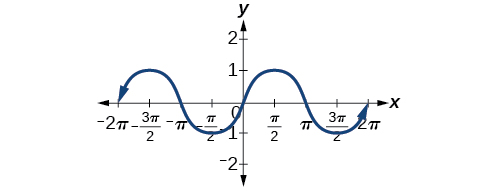
L'examen à nouveau des fonctions sinus et cosinus sur un domaine centré sur l'\(y\)axe -permet de révéler les symétries. Comme nous pouvons le voir sur la figure\(\PageIndex{6}\), la fonction sinusoïdale est symétrique par rapport à l'origine. Rappelons dans The Other Trigonometric Functions que nous avons déterminé à partir du cercle unitaire que la fonction sinusoïdale est une fonction étrange car\(\sin(−x)=−\sin\space x\). Nous pouvons maintenant voir clairement cette propriété sur le graphique.
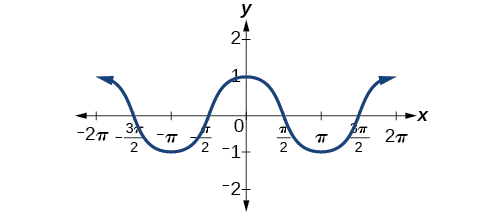
La figure\(\PageIndex{7}\) montre que la fonction cosinus est symétrique par rapport à l'\(y\)axe. Encore une fois, nous avons déterminé que la fonction cosinus est une fonction paire. Maintenant, nous pouvons le voir sur le graphique\(\cos(−x)=\cos\space x\).
Les fonctions sinus et cosinus présentent plusieurs caractéristiques distinctes :
- Ce sont des fonctions périodiques d'une durée de\(2\pi\).
- Le domaine de chaque fonction est\((−\infty,\infty)\) et la plage est\([ −1,1 ]\).
- Le graphe de\(y=\sin\space x\) est symétrique par rapport à l'origine, car il s'agit d'une fonction étrange.
- Le graphe de\(y=\cos\space x\) est symétrique par rapport à leur\(y\) axe, car il s'agit d'une fonction paire.
Étude des fonctions sinusoïdales
Comme nous pouvons le voir, les fonctions sinus et cosinus ont une période et une plage régulières. Si nous observons les vagues ou les ondulations de l'océan sur un étang, nous verrons qu'elles ressemblent aux fonctions sinusoïdales ou cosinusoïdales. Cependant, ils ne sont pas nécessairement identiques. Certains sont plus grands ou plus longs que d'autres. Une fonction qui a la même forme générale qu'une fonction sinusoïdale ou cosinusoïdale est appelée fonction sinusoïdale. Les formes générales des fonctions sinusoïdales sont les suivantes :
\[y=A\sin(Bx−C)+D\]
et
\[y=A\cos(Bx−C)+D\]
Déterminer la période des fonctions sinusoïdales
En examinant les formes des fonctions sinusoïdales, nous pouvons voir qu'il s'agit de transformations des fonctions sinus et cosinus. Nous pouvons utiliser ce que nous savons des transformations pour déterminer la période.
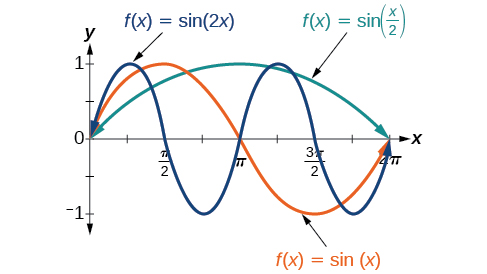
Dans la formule générale,\(B\) est lié à la période par\(P=\dfrac{2\pi}{|B|}\). Si\(|B|>1\), alors la période est inférieure à\(2\pi\) et la fonction subit une compression horizontale, alors que si\(| B |<1\), alors la période est supérieure à\(2\pi\) et la fonction subit un étirement horizontal. Par exemple,\(f(x)=\sin(x)\)\(B=1\), il en est\(2\pi\) ainsi de la période que nous connaissions. Si\(f(x)=\sin(2x)\), alors\(B=2\), la période l'est\(\pi\) et que le graphique est compressé. Si\(f(x)=\sin\left(\dfrac{x}{2}\right)\), alors\(B=\dfrac{1}{2}\), la période l'est\(4\pi\) et que le graphique est étiré. Remarquez sur la figure\(\PageIndex{8}\) comment la période est indirectement liée à\(|B|\).
Si nous laissons\(C=0\) et\(D=0\) dans les équations de forme générale des fonctions sinus et cosinus, nous obtenons les formes
- \(y=A\sin(Bx)\)
- \(y=A\cos(Bx)\)
La période est\(\dfrac{2\pi}{|B|}\).
Déterminez la durée de la fonction\(f(x)=\sin\left(\dfrac{\pi}{6}x\right)\).
Solution
Commençons par comparer l'équation à la forme générale\(y=A\sin(Bx)\).
Dans l'équation donnée\(B=\dfrac{\pi}{6}\), la période sera donc
\[ \begin{align*} P&=\dfrac{2\pi}{|B|} \\[4pt] &=\dfrac{2\pi}{\dfrac{\pi}{6}} \\ &=2\pi ⋅ \dfrac{6}{\pi} \\[4pt] &=12 \end{align*}\]
Déterminez la durée de la fonction\(g(x)=\cos(\frac{x}{3})\).
- Réponse
-
\(6\pi\)
Déterminer l'amplitude
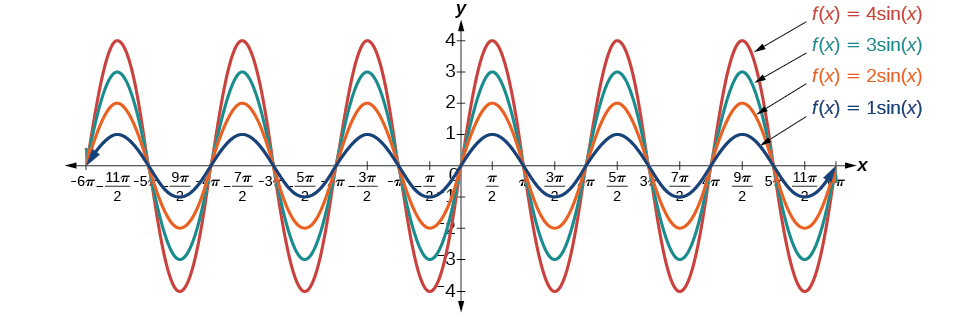
Pour en revenir à la formule générale d'une fonction sinusoïdale, nous avons analysé la relation entre\(B\) la variable et la période. Passons maintenant à la variable\(A\) afin d'analyser son lien avec l'amplitude, ou la plus grande distance par rapport au repos. \(A\)représente le facteur d'étirement vertical, et sa valeur absolue\(|A|\) est l'amplitude. Les maxima locaux seront une distance\(|A|\) au-dessus de la ligne médiane verticale du graphique, qui est la droite\(x=D\) ; car\(D=0\) dans ce cas, la ligne médiane est l'axe X. Les minima locaux seront situés à la même distance en dessous de la ligne médiane. Si\(| A |>1\), la fonction est étendue. Par exemple, l'amplitude de\(f(x)=4 sin x\) est le double de l'amplitude de
\(f(x)=2\sin x\)
Si\(| A |<1\), la fonction est compressée. La figure\(\PageIndex{9}\) compare plusieurs fonctions sinusoïdales avec différentes amplitudes.
Si nous laissons\(C=0\) et\(D=0\) dans les équations de forme générale des fonctions sinus et cosinus, nous obtenons les formes
\[\begin{align} y=A\sin(Bx)\text { and } y=A\cos(Bx) \end{align}\]
L'amplitude est\(A\) et la hauteur verticale à partir de la ligne médiane est\(|A|\). En outre, notez dans l'exemple que
\[|A| = amplitude = \dfrac{1}{2}∣maximum − minimum|\]
Quelle est l'amplitude de la fonction sinusoïdale\(f(x)=−4\sin(x)\) ? La fonction est-elle étendue ou compressée verticalement ?
Solution
Commençons par comparer la fonction à la forme simplifiée\(y=A\sin(Bx)\).
Dans la fonction donnée\(A=−4\), l'amplitude est donc\(| A |=| −4 |=4\). La fonction est étendue.
Analyse
La valeur négative de\(A\) entraîne une réflexion sur l'\(x\)axe -de la fonction sinusoïdale, comme le montre la figure\(\PageIndex{10}\).
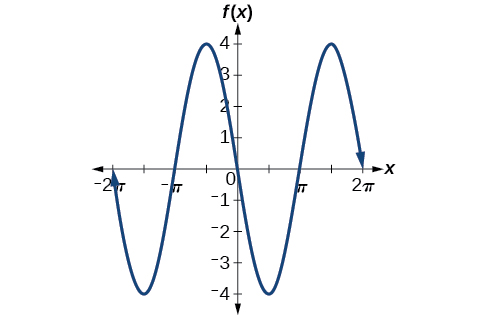
Quelle est l'amplitude de la fonction sinusoïdale\(f(x)=\frac{1}{2}\sin(x)\) ? La fonction est-elle étendue ou compressée verticalement ?
- Réponse
-
\(\frac{1}{2}\)compressé
Analyse des graphes des variations de\(y = \sin\space x\) et\(y = \cos\space x\)
Maintenant que nous comprenons comment\(A\) et nous sommes\(B\) liés à l'équation de forme générale pour les fonctions sinus et cosinus, nous allons explorer les variables\(C\) et\(D\). Rappelez-vous le formulaire général :
\[y=A\sin(Bx-C)+D\qquad \text{ and } \qquad y=A\cos(Bx-C)+D\]
ou
\[y=A\sin\left (B\left (x-\dfrac{C}{B} \right ) \right )+D \qquad \text{ and } \qquad y=A\cos\left (B\left (x-\dfrac{C}{B} \right ) \right )+D\]
La valeur\(\frac{C}{B}\) d'une fonction sinusoïdale est appelée décalage de phase, ou déplacement horizontal de la fonction sinusoïdale ou cosinusoïdale de base. Si\(C>0\), le graphique se déplace vers la droite. Si\(C<0\), le graphique se déplace vers la gauche. Plus la valeur de est élevée\(| C |\), plus le graphique est décalé. La figure\(\PageIndex{11}\) montre que le graphique des\(f(x)=\sin(x−\pi)\) décalages vers la droite par\(\pi\) unités, qui est supérieur à ce que nous voyons dans le graphique de\(f(x)=\sin\left(x−\frac{\pi}{4}\right)\), qui se déplace vers la droite par\(\frac{\pi}{4}\) unités.
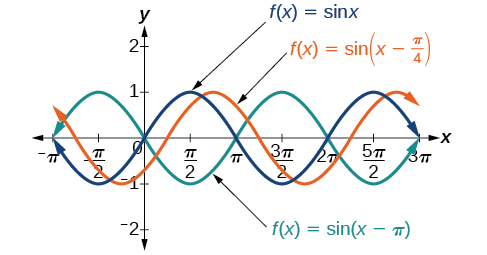
Tout en\(C\) se rapportant au décalage horizontal,\(D\) indique le décalage vertical par rapport à la ligne médiane dans la formule générale d'une fonction sinusoïdale. Voir la figure\(\PageIndex{12}\). La ligne médiane de la fonction\(y=\cos(x)+D\) est\(y=D\).
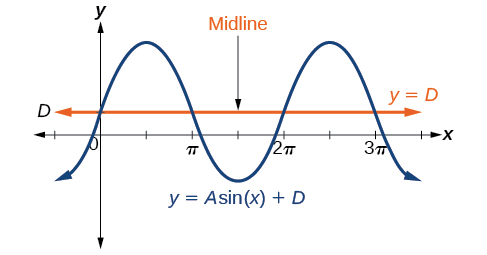
Toute valeur\(D\) autre que zéro déplace le graphique vers le haut ou vers le bas. La figure est\(\PageIndex{13}\) \(f(x)=\sin x\)comparée à\(f(x)=\sin x+2\), qui est décalée\(2\) d'unités vers le haut sur un graphique.
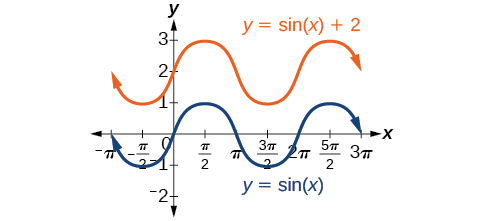
Étant donné qu'une équation sous la forme\(f(x)=A \sin (Bx−C)+D\) ou\(f(x)=A \cos (Bx−C)+D\),\(\frac{C}{D}\) est le décalage de phase et\(D\) est le décalage vertical.
Déterminez la direction et l'amplitude du décalage de phase pour\(f(x)=\sin\left(x+\frac{\pi}{6}\right)−2\).
Solution
Commençons par comparer l'équation à la forme générale\(y=A\sin(Bx−C)+D\).
Dans l'équation donnée, notez que\(B=1\) et\(C=−\frac{\pi}{6}\). Donc, le décalage de phase est
\[\begin{align*} \dfrac{C}{B}&= -\frac{\frac{\pi}{6}}{1}\\ &= -\frac{\pi}{6} \end{align*}\]
ou\(\frac{\pi}{6}\) des unités vers la gauche.
Analyse
Nous devons faire attention au signe de l'équation pour la forme générale d'une fonction sinusoïdale. L'équation montre un signe moins avant\(C\). \(f(x)=\sin(x+\frac{\pi}{6})−2\)Peut donc être réécrit comme\(f(x)=\sin\left(x−\left(−\frac{\pi}{6}\right)\right)−2\). Si la valeur de\(C\) est négative, le décalage se fait vers la gauche.
Déterminez la direction et l'amplitude du décalage de phase pour\(f(x)=3\cos\left(x−\frac{\pi}{2}\right)\).
- Réponse
-
\(\frac{\pi}{2}\); droite
Déterminez la direction et l'amplitude du décalage vertical pour\(f(x)=\cos(x)−3\).
Solution
Commençons par comparer l'équation à la forme générale\(y=A\cos(Bx−C)+D\).
Dans l'équation donnée, le décalage est\(D=−3\) donc exprimé en\(3\) unités vers le bas.
Déterminez la direction et l'amplitude du décalage vertical pour\(f(x)=3\sin(x)+2\).
- Réponse
-
\(2\)unités en hausse
- Déterminez l'amplitude comme\(| A |\).
- Déterminez la période comme\(P=\frac{2\pi}{| B |}\).
- Déterminez le décalage de phase comme\(\frac{C}{B}\).
- Déterminez la ligne médiane comme\(y=D\).
Déterminez la ligne médiane, l'amplitude, la période et le décalage de phase de la fonction\(y=3\sin (2x)+1\).
Solution
Commençons par comparer l'équation à la forme générale\(y=A\sin (Bx−C)+D\).
\(A=3\), donc l'amplitude est\(| A |=3\).
Ensuite\(B=2\), il en va de même pour la période\(P=\dfrac{2\pi}{| B |}=\dfrac{2\pi}{2}=\pi\).
Il n'y a pas de constante ajoutée entre parenthèses, donc\(C=0\) le décalage de phase l'est\(\dfrac{C}{B}=\dfrac{0}{2}=0\).
Enfin\(D=1\), il en va de même pour la ligne médiane\(y=1\).
Analyse
En inspectant le graphique, nous pouvons déterminer que la période est\(\pi\), la ligne médiane est\(y=1\) et l'amplitude est\(3\). Voir la figure\(\PageIndex{14}\).
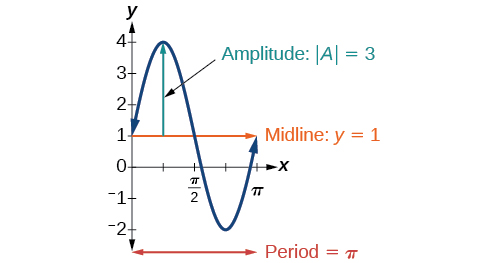
Déterminez la ligne médiane, l'amplitude, la période et le décalage de phase de la fonction\(y=\frac{1}{2}\cos \left(\frac{x}{3}−\frac{\pi}{3}\right)\).
- Réponse
-
ligne médiane :\(y=0\) ; amplitude :\(| A |=\frac{1}{2}\) ; période :\(P=\frac{2\pi}{| B |}=6π\) ; décalage de phase :\(\frac{C}{B}=\pi\)
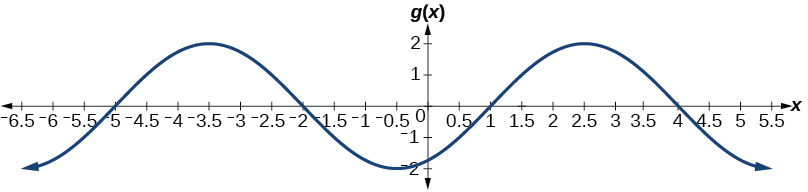
Déterminez la formule de la fonction cosinus dans la figure\(\PageIndex{15}\).
![Un graphique de -0,5 cos (x) +0,5. Le graphique a une amplitude de 0,5. Le graphique a une période de 2 pi. Le graphique a une plage de [0, 1]. Le graphique est également reflété autour de l'axe x à partir de la fonction parent cos (x).](https://math.libretexts.org/@api/deki/files/6903/CNX_Precalc_Figure_06_01_015.jpg)
Solution
Pour déterminer l'équation, nous devons identifier chaque valeur sous la forme générale d'une fonction sinusoïdale.
\(y=A\sin (Bx−C)+D\)
\(y=A\cos (Bx−C)+D\)
Le graphique peut représenter une fonction sinusoïdale ou cosinusoïdale décalée et/ou réfléchie. Quand\(x=0\), le graphique a un point extrême,\((0,0)\). Puisque la fonction cosinus a un point extrême pour\(x=0\), écrivons notre équation en termes de fonction cosinus.
Commençons par la ligne médiane. Nous pouvons voir que le graphique monte et descend à égale distance au-dessus et en dessous\(y=0.5\). Cette valeur, qui est la ligne médiane, se trouve\(D\) dans l'équation, donc\(D=0.5\).
La plus grande distance au-dessus et en dessous de la ligne médiane est l'amplitude. Les maxima sont des\(0.5\) unités au-dessus de la ligne médiane et les minima sont des\(0.5\) unités situées en dessous de la ligne médiane. Donc\(| A |=0.5\). Une autre façon de déterminer l'amplitude serait de reconnaître que la différence entre la hauteur des maxima et des minima locaux est\(1\) égale à\(| A |=\frac{1}{2}=0.5\). De plus, le graphique est réfléchi autour de l'\(x\)axe -de sorte que\(A=−0.5\).
Le graphe n'est pas étiré ou compressé horizontalement, donc\(B=1\) ; et le graphe n'est pas décalé horizontalement, donc\(C=0\).
En rassemblant tout cela,
\(g(x)=−0.5\cos (x)+0.5\)
Déterminez la formule de la fonction sinusoïdale dans la figure\(\PageIndex{16}\).
![Un graphique de sin (x) +2. Période de 2 pi, amplitude de 1 et plage de [1, 3].](https://math.libretexts.org/@api/deki/files/6904/CNX_Precalc_Figure_06_01_016.jpg)
- Réponse
-
\(f(x)=\sin(x)+2\)
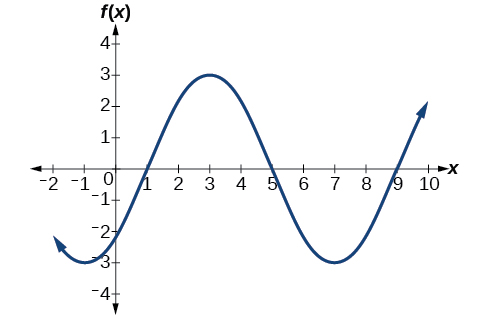
Déterminez l'équation de la fonction sinusoïdale dans la figure\(\PageIndex{17}\).
![Un graphique de 3cos (pi/3x-pi/3) -2. Le graphe a une amplitude de 3, une période de 6, une plage de [-5,1].](https://math.libretexts.org/@api/deki/files/6905/CNX_Precalc_Figure_06_01_017.jpg)
Solution
Avec la valeur la plus élevée à\(1\) et la valeur la plus faible à\(−5\), la ligne médiane se situera à mi-chemin entre at\(−2\). Donc\(D=−2\).
La distance entre la ligne médiane et la valeur la plus élevée ou la plus basse donne une amplitude de\(| A |=3\).
La période du graphique est\(6\), qui peut être mesurée du pic au\(x=1\) pic suivant\(x=7\), ou à partir de la distance entre les points les plus bas. Par conséquent,\(P=\dfrac{2\pi}{| B |}=6\). En utilisant la valeur positive pour\(B\), nous constatons que
\[\begin{align*} B&=\dfrac{2\pi}{P}\\ &=\dfrac{2\pi}{6}\\ &=\dfrac{\pi}{3} \end{align*}\]
Jusqu'à présent, notre équation est\(y=3\sin\left(\dfrac{\pi}{3}x−C\right)−2\) soit\(y=3\cos\left(\dfrac{\pi}{3}x−C\right)−2\) soit. Pour la forme et le décalage, nous avons plusieurs options. Nous pourrions écrire ceci de la manière suivante :
- un cosinus décalé vers la droite
- un cosinus négatif décalé vers la gauche
- un sinus décalé vers la gauche
- un sinus négatif décalé vers la droite
Bien que chacune d'entre elles soit correcte, les décalages en cosinus sont plus faciles à utiliser que les décalages sinusoïdaux dans ce cas, car ils impliquent des valeurs entières. Notre fonction devient donc
\[\begin{align*} y&=3\cos \left (\frac{\pi}{3}x-\dfrac{\pi}{3} \right )-2 \qquad \text{or} \\ y&=-3\cos \left (\dfrac{\pi}{3}x+\dfrac{2\pi}{3} \right )-2 \end{align*}\]
Encore une fois, ces fonctions sont équivalentes, de sorte que les deux produisent le même graphique.
Écrivez une formule pour la fonction illustrée dans la figure\(\PageIndex{18}\).
![Un graphique de 4sin ((pi/5) x-pi/5) +4. Le graphique a une période de 10, une amplitude de 4, une plage de [0,8].](https://math.libretexts.org/@api/deki/files/6906/CNX_Precalc_Figure_06_01_018n.jpg)
- Réponse
-
deux possibilités :\(y=4\sin\left(\dfrac{\pi}{5}x−\dfrac{\pi}{5}\right)+4\) ou\(y=−4\sin\left(\dfrac{\pi}{5}x+\dfrac{4\pi}{5}\right)+4\)
Représentation graphique des variations de\(y = \sin\space x\) et\(y = \cos\space x\)
Tout au long de cette section, nous avons découvert les types de variations des fonctions sinusoïdales et cosinusoïdales et avons utilisé ces informations pour écrire des équations à partir de graphes. Nous pouvons maintenant utiliser les mêmes informations pour créer des graphiques à partir d'équations.
Au lieu de se concentrer sur les équations de forme générales
\(y=A\sin(Bx-C)+D \text{ and } y=A\cos(Bx-C)+D\)
nous allons laisser\(C=0\)\(D=0\) et travailler avec une forme simplifiée des équations dans les exemples suivants.
- Identifiez l'amplitude,\(| A |\).
- Identifiez la période,\(P=\dfrac{2\pi}{| B |}\).
- Commencez par l'origine, la fonction augmentant vers la droite si elle\(A\) est positive ou décroissante si elle\(A\) est négative.
- À\(x=\dfrac{\pi}{2| B |}\) il y a un maximum local pour\(A>0\) ou un minimum pour\(A<0\), avec\(y=A\).
- La courbe revient sur l'axe X à\(x=\dfrac{\pi}{| B |}\).
- Il existe un minimum local pour\(A>0\) (maximum pour\(A<0\)) à\(x=\dfrac{3\pi}{2| B |}\) avec\(y=–A\).
- La courbe revient à nouveau sur l'axe x à\(x=\dfrac{\pi}{2| B |}\).
Esquissez un graphique de\(f(x)=−2\sin\left(\dfrac{\pi x}{2}\right)\).
Solution
Commençons par comparer l'équation à la forme\(y=A\sin(Bx)\).
- Étape 1 Nous pouvons voir à partir de l'équation que\(A=−2\), donc l'amplitude est de 2.
\(|A|=2 \)
- Étape 2 L'équation montre que\(B=\dfrac{\pi}{2}\), donc, la période est
\[\begin{align*} P&=\dfrac{2\pi}{\dfrac{\pi}{2}}\\ &=2\pi \cdot \dfrac{2}{\pi}\\ &=4 \end{align*}\]
- Étape 3 Parce que\(A\) c'est négatif, le graphique descend à mesure que l'on se déplace vers la droite de l'origine.
- Étape 4. Les\(x\) -intercepts se situent au début d'une période\(x=0\), les points médians horizontaux se situent à\(x=2\) et à la fin d'une période à\(x=4\).
Les quarts de points incluent le minimum à\(x=1\) et le maximum à\(x=3\). Un minimum local se produira en\(2\) unités en dessous de la ligne médiane\(x=1\), à, et un maximum local se produira aux\(2\) unités au-dessus de la ligne médiane, à\(x=3\). La figure\(\PageIndex{19}\) montre le graphique de la fonction.
![Un graphique de -2sin ((pi/2) x). Le graphe a une plage de [-2,2], une période de 4 et une amplitude de 2.](https://math.libretexts.org/@api/deki/files/6907/CNX_Precalc_Figure_06_01_019.jpg)
Esquissez un graphique de\( g(x)=−0.8\cos(2x)\). Déterminez la ligne médiane, l'amplitude, la période et le décalage de phase.
- Réponse
-
![Un graphique de -0,8 cos (2x). Le graphe a une plage de [-0,8, 0,8], une période de pi, une amplitude de 0,8 et est réfléchi autour de l'axe x par rapport à sa fonction parent cos (x).](https://math.libretexts.org/@api/deki/files/6908/CNX_Precalc_Figure_06_01_020.jpg)
Figurine\(\PageIndex{20}\) ligne médiane :\(y=0\) ; amplitude :\(| A |=0.8\) ; période :\(P=\dfrac{2\pi}{| B |}=\pi\) ; décalage de phase :\(\dfrac{C}{B}=0\) ou aucun
- Exprimez la fonction sous la forme générale\(y=A\sin(Bx−C)+D\) ou\(y=A\cos(Bx−C)+D\).
- Identifiez l'amplitude,\(| A |\).
- Identifiez la période,\(P=\dfrac{2\pi}{| B |}\).
- Identifiez le décalage de phase,\(\dfrac{C}{B}\).
- Tracez le graphique du\(f(x)=A\sin(Bx)\) décalage vers la droite ou vers la gauche\(\dfrac{C}{B}\) et vers le haut ou vers le bas\(D\).
Esquissez un graphique de\(f(x)=3\sin\left(\dfrac{\pi}{4x}−\dfrac{\pi}{4}\right)\).
Solution
- Étape 1 La fonction est déjà écrite sous une forme générale :\(f(x)=3\sin\left(\dfrac{\pi}{4x}−\dfrac{\pi}{4}\right)\) .Ce graphique aura la forme d'une fonction sinusoïdale, commençant par la ligne médiane et augmentant vers la droite.
- Étape 2 \(| A |=| 3 |=3\). L'amplitude est\(3\).
- Étape 3. Depuis\(| B |=| \dfrac{\pi}{4} |=\dfrac{\pi}{4}\), nous déterminons la période comme suit.
\[\begin{align*} P&=\dfrac{2\pi}{|B|}\\ &=\dfrac{2\pi}{\dfrac{\pi}{4}}\\ &=2\pi \cdot \dfrac{4}{\pi}\\ &=8 \end{align*}\]
La période est\(8\).
- Étape 4. Puisque\(C=\dfrac{\pi}{4}\), le décalage de phase est
\[\dfrac{C}{B}=\dfrac{\dfrac{\pi}{4}}{\dfrac{\pi}{4}}=1\].
Le décalage de phase est\(1\) unitaire.
- Étape 5. La figure\(\PageIndex{21}\) montre le graphique de la fonction.
Dessinez un graphique de\(g(x)=−2\cos\left(\dfrac{\pi}{3}x+\dfrac{\pi}{6}\right)\). Déterminez la ligne médiane, l'amplitude, la période et le décalage de phase.
- Réponse
-
Figurine\(\PageIndex{22}\) ligne médiane :\(y=0\) ; amplitude :\(| A |=2\) ; période :\(P=\dfrac{2\pi}{| B |}=6\) ; décalage de phase :\(\dfrac{C}{B}=−\dfrac{1}{2}\)
Étant donné\(y=−2cos\left(\dfrac{\pi}{2}x+\pi\right)+3\), déterminez l'amplitude, la période, le décalage de phase et le décalage horizontal. Tracez ensuite la fonction.
Solution
Commencez par comparer l'équation à la forme générale.
\(y=A\cos(Bx−C)+D\)
- Étape 1 La fonction est déjà écrite sous forme générale.
- Étape 2 Depuis\(A=−2\), l'amplitude est\(| A |=2\).
- Étape 3. \(| B |=\dfrac{\pi}{2}\), donc la période est\(P=\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\). La période est de 4.
- Étape 4. \(C=−\pi\), nous calculons donc le décalage de phase comme\(\dfrac{C}{B}=−\dfrac{\pi}{\dfrac{\pi}{2}}=−\pi⋅\dfrac{2}{\pi}=−2\). Le décalage de phase est\(−2\).
- Étape 5. \(D=3\), donc la ligne médiane est et\(y=3\) le décalage vertical est vers le haut\(3\).
Comme\(A\) il est négatif, le graphe de la fonction cosinus s'est reflété autour de\(x\) l'axe.
La figure\(\PageIndex{23}\) montre un cycle du graphe de la fonction.
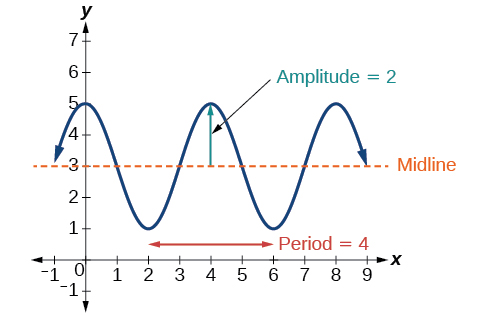
Utilisation des transformations des fonctions sinusoïdale et cosinusoïdale
Nous pouvons utiliser les transformations des fonctions sinusoïdales et cosinusoïdales dans de nombreuses applications. Comme mentionné au début du chapitre, le mouvement circulaire peut être modélisé à l'aide de la fonction sinusoïdale ou cosinusoïdale.
Un point pivote autour d'un cercle de rayon\(3\) centré sur l'origine. Esquissez un graphique de la\(y\) coordonnée du point en fonction de l'angle de rotation.
Solution
Rappelez-vous que, pour un point d'un cercle de rayon\(r\), la\(y\) coordonnée -du point est\(y=r \sin(x)\), donc dans ce cas, nous obtenons l'équation\(y(x)=3 \sin(x)\). La constante\(3\) provoque un étirement vertical des\(y\) valeurs -de la fonction par un facteur de\(3\), comme nous pouvons le voir sur le graphique de la figure\(\PageIndex{24}\).
![Un graphique de 3sin (x). Le graphe a une période de 2 pi, une amplitude de 3 et une plage de [-3,3].](https://math.libretexts.org/@api/deki/files/6912/CNX_Precalc_Figure_06_01_023.jpg)
Analyse
Remarquez que la période de la fonction est immobile\(2\pi\) ; en faisant le tour du cercle, nous revenons au point\((3,0)\) pour\(x=2\pi,4\pi,6\pi,\)... Parce que les sorties du graphe oscilleront désormais entre\(–3\) et\(3\), l'amplitude de l'onde sinusoïdale est\(3\).
Quelle est l'amplitude de la fonction\(f(x)=7\cos(x)\) ? Esquissez un graphique de cette fonction.
- Réponse
-
![Un graphique de 7cos (x). Le graphe a une amplitude de 7, une période de 2 pi et une plage de [-7,7].](https://math.libretexts.org/@api/deki/files/6913/CNX_Precalc_Figure_06_01_024.jpg)
Figurine\(\PageIndex{25}\)
Un cercle de rayon\(3\) ft est monté avec son centre à\(4\) pieds au-dessus du sol. Le point le plus proche du sol est étiqueté\(P\), comme indiqué sur la figure\(\PageIndex{26}\). Esquissez un graphique de la hauteur au-dessus du sol du point\(P\) lorsque le cercle pivote, puis trouvez une fonction qui donne la hauteur en termes d'angle de rotation.
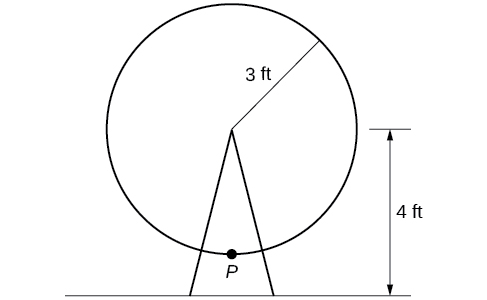
Solution
En esquissant la hauteur, nous remarquons qu'elle commencera à\(1\) pieds au-dessus du sol, puis augmentera jusqu'à\(7\) pieds au-dessus du sol et continuera à osciller\(3\) pieds au-dessus et en dessous de la valeur centrale de\(4\) pieds, comme le montre la figure\(\PageIndex{27}\).
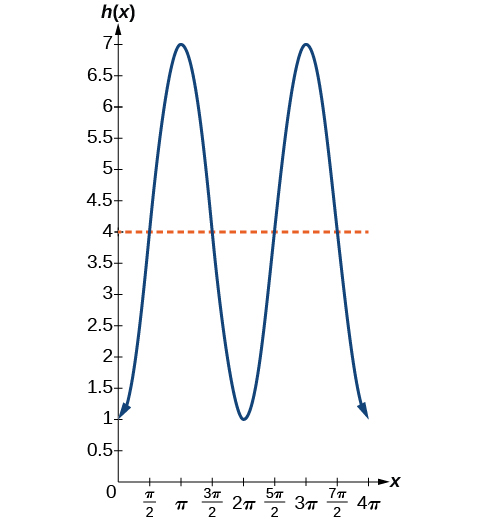
Bien que nous puissions utiliser une transformation de la fonction sinus ou cosinus, nous commençons par rechercher des caractéristiques qui rendraient une fonction plus facile à utiliser que l'autre. Utilisons une fonction cosinus, car elle commence à la valeur la plus élevée ou la plus basse, tandis qu'une fonction sinusoïdale commence à la valeur moyenne. Un cosinus standard commence à la valeur la plus élevée et ce graphique commence à la valeur la plus basse. Nous devons donc intégrer une réflexion verticale.
Ensuite, nous voyons que le graphe oscille\(3\) au-dessus et en dessous du centre, alors qu'un cosinus de base a une amplitude de\(1\). Ce graphique a donc été étiré verticalement\(3\), comme dans le dernier exemple.
Enfin, pour déplacer le centre du cercle jusqu'à une hauteur de\(4\), le graphique a été décalé verticalement de\(4\). En combinant ces transformations, nous constatons que
\(y=−3\cos(x)+4\)
Un poids est attaché à un ressort qui est ensuite suspendu à une planche, comme le montre la figure\(\PageIndex{28}\). Lorsque le ressort oscille de haut en bas, la position\(y\) du poids par rapport à la planche varie de\(–1\) l'intérieur. (à l'époque\(x=0\)) pour\(–7\) gagner. (parfois\(x=π\)) en dessous du plateau. Supposons que la position de\(y\) est donnée en tant que fonction sinusoïdale de\(x\). Esquissez un graphique de la fonction, puis trouvez une fonction cosinusoïdale qui donne la position\(y\) en termes de\(x\).
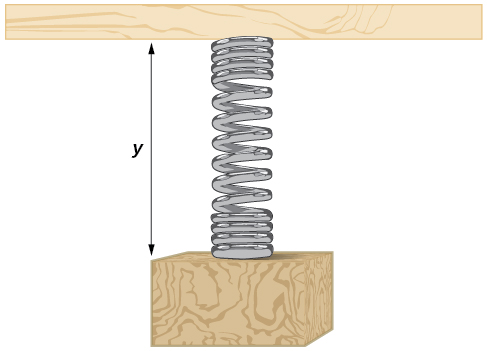
- Réponse
-
\(y=3\cos(x)−4\)
![Un graphe en cosinus avec une plage [-1, -7]. La période est de 2 pi. Maximums locaux à (0, -1), (2 pi, -1) et (4 pi, -1). Minimums locaux à (pi, -7) et (3pi, -7).](https://math.libretexts.org/@api/deki/files/6917/CNX_Precalc_Figure_06_01_027.jpg)
Figurine\(\PageIndex{29}\)
Le London Eye est une énorme grande roue d'un diamètre de\(135\) mètres (\(443\)pieds). Il effectue une rotation toutes les\(30\) minutes. Les cavaliers montent à bord depuis une plate-forme\(2\) située à quelques mètres du sol. Exprime la hauteur du cycliste au-dessus du sol en fonction du temps en minutes.
Solution
Avec un diamètre de\(135\) m, la roue a un rayon de\(67.5\) m. La hauteur oscillera avec l'amplitude\(67.5\) m au-dessus et en dessous du centre.
Les passagers montent à\(2\) m au-dessus du niveau du sol, de sorte que le centre de la roue doit être situé à\(67.5+2=69.5\) m au-dessus du niveau du sol. La ligne médiane de l'oscillation sera à\(69.5\) m.
La roue met\(30\) quelques minutes à effectuer sa\(1\) révolution, de sorte que la hauteur oscille en\(30\) quelques minutes.
Enfin, comme le pilote monte à bord au point le plus bas, la hauteur commence à la valeur la plus faible et augmente en suivant la forme d'une courbe en cosinus réfléchie verticalement.
- Amplitude :\(67.5\), donc\(A=67.5\)
- Ligne médiane :\(69.5\), donc\(D=69.5\)
- Période :\(30\), donc\(B=\dfrac{2\pi}{30}=\dfrac{\pi}{15}\)
- Forme :\(−\cos(t)\)
Une équation pour la taille du cavalier serait
\(y=−67.5\cos\left(\dfrac{\pi}{15}t\right)+69.5\)
où\(t\) est exprimé en minutes et\(y\) est mesuré en mètres.
Accédez à ces ressources en ligne pour des instructions et des exercices supplémentaires avec des graphiques des fonctions sinusoïdales et cosinusoïdales
- Amplitude et période du sinus et du cosinus
- Traductions de Sine et Cosine
- Représentation graphique des transformations en sinus et en cosinus
- Création graphique de la fonction sinusoïdale
Équations clés
| Fonctions sinusoïdales |
\(f(x)=A\sin(Bx−C)+D\) \(f(x)=A\cos(Bx−C)+D\) |
Concepts clés
- Les fonctions périodiques se répètent après une valeur donnée. La plus petite de ces valeurs est la période. Les fonctions sinusoïdales et cosinusoïdales de base ont une période de\(2\pi\).
- La fonction\(\sin x\) est étrange, donc son graphe est symétrique par rapport à l'origine. La fonction\(\cos x\) étant paire, son graphe est symétrique par rapport à l'axe y.
- Le graphe d'une fonction sinusoïdale a la même forme générale qu'une fonction sinusoïdale ou cosinusoïdale.
- Dans la formule générale d'une fonction sinusoïdale, la période est\(P=\dfrac{2\pi}{| B |}\). Voir l'exemple\(\PageIndex{1}\).
- Dans la formule générale d'une fonction sinusoïdale,\( | A |\) représente l'amplitude. Si\(| A |>1\), la fonction est étirée, alors que si\(| A |<1\), la fonction est compressée. Voir l'exemple\(\PageIndex{2}\).
- La valeur\(\dfrac{C}{B}\) de la formule générale d'une fonction sinusoïdale indique le décalage de phase. Voir l'exemple\(\PageIndex{3}\).
- La valeur\(D\) de la formule générale d'une fonction sinusoïdale indique le décalage vertical par rapport à la ligne médiane. Voir l'exemple\(\PageIndex{4}\).
- Des combinaisons de variations de fonctions sinusoïdales peuvent être détectées à partir d'une équation. Voir l'exemple\(\PageIndex{5}\).
- L'équation d'une fonction sinusoïdale peut être déterminée à partir d'un graphique. Voir Exemple\(\PageIndex{6}\) et Exemple\(\PageIndex{7}\).
- Une fonction peut être représentée graphiquement en identifiant son amplitude et sa période. Voir Exemple\(\PageIndex{8}\) et Exemple\(\PageIndex{9}\).
- Une fonction peut également être représentée graphiquement en identifiant son amplitude, sa période, son décalage de phase et son décalage horizontal. Voir l'exemple\(\PageIndex{10}\).
- Les fonctions sinusoïdales peuvent être utilisées pour résoudre des problèmes du monde réel. Voir Exemple\(\PageIndex{11}\)\(\PageIndex{12}\), Exemple et Exemple\(\PageIndex{13}\).


