Mathématiques essentielles
- Page ID
- 193982
Arithmétique exponentielle
La notation exponentielle est utilisée pour exprimer de très grands et de très petits nombres sous la forme d'un produit de deux nombres. Le premier chiffre du produit, le terme numérique, est généralement un nombre compris entre 1 et 10. Le deuxième nombre du produit, le terme exponentiel, s'écrit 10 avec un exposant. Voici quelques exemples de notation exponentielle :
\ [\ begin {align*}
1000&=1 × 10^3 \ \
100&=1 × 10^2 \ \
10&=1 × 10^1 \ \
1&=1 × 10^0 \ \
0,1 &=1 × 10^ {-1} \ \
0,001} \ 0,001 & = 1 × 10^ {−3} \ \
2386&=2,386 × 1000 = 2,386 × 10^3 \
0,123&=1,23 × 0,1 = 1,23 × 10^ { −1}
\ end {align*} \ nonumber \]
La puissance (exposant) de 10 est égale au nombre de décimales décalées pour donner le nombre numérique. La méthode exponentielle est particulièrement utile pour la notation de tous les grands et très petits nombres. Par exemple, 1 230 000 000 = 1,23 × 10 9 et 0,000000036 = 3,6 × 10 −10.
Ajout d'exponentielles
Convertissez tous les nombres avec la même puissance de 10, ajoutez les termes numériques des nombres et, le cas échéant, reconvertissez le terme numérique en un nombre compris entre 1 et 10 en ajustant le terme exponentiel.
Ajoutez 5,00 × 10 −5 et 3,00 × 10 −3.
Solution 1
\ [\ begin {align*}
3,00×10^ {−3} &=300 × 10^ {−5} \ \
(5,00 × 10^ {−5}) + (300 × 10^ {−5}) + (300 × 10^ {−5}) &=305 × 10^ {−3}
\ end {align*} \ nonnumber \]
Soustraction d'exponentielles
Convertissez tous les nombres avec la même puissance de 10, prenez la différence entre les termes numériques et, le cas échéant, reconvertissez le terme numérique en un nombre compris entre 1 et 10 en ajustant le terme exponentiel.
Soustrayez 4,0 × 10 −7 de 5,0 × 10 −6.
Solution 1
\ [4,0×10^ {−7} =0,40 × 10^ {−6} \ \
(5,0 × 10^ {−6}) − (0,40 × 10^ {−6}) =4,6 × 10^ {−6} \ aucun nombre \]
Multiplication des exponentielles
Multipliez les termes numériques de la manière habituelle et ajoutez les exposants des termes exponentiels.
Multipliez 4,2 × 10 −8 par 2,0 × 10 3.
Solution 1
\[(4.2×10^{−8})×(2.0×10^3)=(4.2×2.0)×10^{(−8)+(+3)}=8.4×10^{−5} \nonumber \]
Division des exponentielles
Divisez le terme numérique du numérateur par le terme numérique du dénominateur et soustrayez les exposants des termes exponentiels.
Divisez 3,6 × 10 5 par 6,0 × 10 −4.
Solution 1
\[\dfrac{3.6×10^{−5}}{6.0×10^{−4}}=\left(\dfrac{3.6}{6.0}\right)×10^{(−5)−(−4)}=0.60×10^{−1}=6.0×10^{−2} \nonumber \]
Mise au carré des exponentielles
Mettez le terme numérique au carré de la manière habituelle et multipliez l'exposant du terme exponentiel par 2.
Mettre au carré le nombre 4,0 × 10 −6.
Solution 1
\[(4.0×10^{−6})^2=4×4×10^{2×(−6)}=16×10^{−12}=1.6×10^{−11} \nonumber \]
Cubage des exponentielles
Coupez le terme numérique de la manière habituelle et multipliez l'exposant du terme exponentiel par 3.
Cube le nombre 2 × 10 4.
Solution 1
\[(2×10^4)^3=2×2×2×10^{3×4}=8×10^{12} \nonumber \]
Prendre les racines carrées des exponentielles
Si nécessaire, diminuez ou augmentez le terme exponentiel afin que la puissance de 10 soit uniformément divisible par 2. Extrayez la racine carrée du terme numérique et divisez le terme exponentiel par 2.
Détermine la racine carrée de 1,6 × 10 −7.
Solution 1
\ [\ begin {align*}
1,6 × 10^ {−7} &=16 × 10^ {−8} \ \
\ sqrt {16 × 10^ {−8}} = \ sqrt {16} × \ sqrt {10^ {−8}} &= \ sqrt {16} ×10^ {− \ large {\ frac {8} {2}}} =4,0 × 10^ {16} × 10^ {−8}} 4}
\ end {align*} \ nonumber \]
Chiffres significatifs
Un apiculteur rapporte qu'il possède 525 341 abeilles. Les trois derniers chiffres du nombre sont évidemment inexacts, car pendant que le gardien comptait les abeilles, certaines d'entre elles sont mortes et d'autres ont éclos ; il est donc très difficile de déterminer le nombre exact d'abeilles. Il aurait été plus exact si l'apiculteur avait déclaré le nombre 525 000. En d'autres termes, les trois derniers chiffres ne sont pas significatifs, sauf pour définir la position de la virgule décimale. Leurs valeurs exactes n'ont aucune signification utile dans cette situation. Lorsque vous présentez toute information sous forme de chiffres, n'utilisez que le nombre de chiffres significatifs que l'exactitude de la mesure le justifie.
L'importance des chiffres significatifs réside dans leur application au calcul fondamental. En plus de la soustraction, la somme ou la différence doit contenir autant de chiffres à droite de la décimale que le nombre le plus petit des nombres utilisés dans le calcul (indiqué par un soulignement dans l'exemple suivant).
Ajoutez 4,383 g et 0,0023 g.
Solution 1
\ [\ begin {align*}
& \ mathrm {4,38 \ underline {3} \ :g} \ \
& \ mathrm {\ underline {0,002 \ underline {3} \ :g}} \ \
& \ mathrm {4,38 \ underline {5} \ :g}
\ end {align*} \ nonnumber \]
Lors de la multiplication et de la division, le produit ou le quotient ne doit pas contenir plus de chiffres que celui du facteur contenant le moins de chiffres significatifs.
Multipliez 0,6238 par 6,6.
Solution 1
\[0.623\underline{8}×6.\underline{6}=4.\underline{1} \nonumber \]
Lorsque vous arrondissez des nombres, augmentez le chiffre retenu de 1 s'il est suivi d'un nombre supérieur à 5 (« arrondir »). Ne modifiez pas le chiffre retenu si les chiffres qui suivent sont inférieurs à 5 (« arrondi vers le bas »). Si le chiffre retenu est suivi de 5, arrondissez vers le haut si le chiffre retenu est impair, ou arrondissez vers le bas s'il est pair (après arrondissement, le chiffre retenu sera donc toujours pair).
L'utilisation de logarithmes et de nombres exponentiels
Le logarithme commun d'un nombre (log) est la puissance à laquelle 10 doit être élevé pour être égal à ce nombre. Par exemple, le logarithme commun de 100 est 2, car 10 doit être élevé à la deuxième puissance pour être égal à 100. D'autres exemples suivent.
| Numéro | Nombre exprimé de façon exponentielle | Logarithme commun |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0,1 | 10 −1 | −1 |
| 0,001 | 10 −3 | −3 |
Quel est le logarithme commun de 60 ? Comme 60 se situe entre 10 et 100, qui ont des logarithmes de 1 et 2, respectivement, le logarithme de 60 est de 1,7782, c'est-à-dire
\[60=10^{1.7782} \nonumber \]
Le logarithme commun d'un nombre inférieur à 1 a une valeur négative. Le logarithme de 0,03918 est −1,4069, ou
\[0.03918=10^{-1.4069}=\dfrac{1}{10^{1.4069}} \nonumber \]
Pour obtenir le logarithme commun d'un nombre, utilisez le bouton de journalisation de votre calculatrice. Pour calculer un nombre à partir de son logarithme, prenez le logarithme inverse du logarithme ou calculez 10 x (où x est le logarithme du nombre).
Le logarithme naturel d'un nombre (ln) est la puissance à laquelle e doit être élevé pour être égal au nombre ; e est la constante 2,7182818. Par exemple, le logarithme naturel de 10 est 2,303, c'est-à-dire
\[10=e^{2.303}=2.7182818^{2.303} \nonumber \]
Pour obtenir le logarithme naturel d'un nombre, utilisez le bouton ln de votre calculatrice. Pour calculer un nombre à partir de son logarithme naturel, entrez le logarithme naturel et prenez l'inverse ln du logarithme naturel, ou calculez e x (où x est le logarithme naturel du nombre).
Les logarithmes sont des exposants ; ainsi, les opérations impliquant des logarithmes suivent les mêmes règles que les opérations impliquant des exposants.
- Le logarithme d'un produit de deux nombres est la somme des logarithmes des deux nombres. \[\log xy= \log x + \log y, \textrm{ and }\ln xy=\ln x + \ln y \nonumber \]
- Le logarithme du nombre résultant de la division de deux nombres est la différence entre les logarithmes des deux nombres. \[\log\dfrac{x}{y}=\log x-\log y,\textrm{ and } \ln\dfrac{x}{y}=\ln x-\ln y \nonumber \]
- Le logarithme d'un nombre élevé à un exposant est le produit de l'exposant et du logarithme du nombre. \[\log x^n=n\log x \textrm{ and }\ln x^n=n\ln x \nonumber \]
La solution des équations quadratiques
Les fonctions mathématiques de cette forme sont appelées polynômes du second ordre ou, plus communément, fonctions quadratiques.
\[ax^2+bx+c=0 \nonumber \]
La solution ou les racines de toute équation quadratique peuvent être calculées à l'aide de la formule suivante :
\[x=\dfrac{-b±\sqrt{b^2−4ac}}{2a} \nonumber \]
Résolution d'équations quadratiques Résolvez l'équation quadratique 3 x 2 + 13 x − 10 = 0.
Solution En substituant les valeurs a = 3, b = 13, c = −10 dans la formule, on obtient
\[x=\dfrac{−13±\sqrt{(13)^2−4×3×(−10)}}{2×3} \nonumber \]
\[x=\dfrac{−13±\sqrt{169+120}}{6}=\dfrac{−13±\sqrt{289}}{6}=\dfrac{−13±17}{6} \nonumber \]
Les deux racines sont donc
\[x=\dfrac{−13+17}{6}=\dfrac{2}{3}\textrm{ and }x=\dfrac{−13−17}{6}=−5 \nonumber \]
Les équations quadratiques construites à partir de données physiques ont toujours de vraies racines, et parmi ces racines réelles, seules celles qui ont des valeurs positives ont souvent une importance.
Graphisme bidimensionnel (x - y)
La relation entre deux propriétés quelconques d'un système peut être représentée graphiquement par un diagramme de données bidimensionnel. Un tel graphe comporte deux axes : un axe horizontal correspondant à la variable indépendante, ou à la variable dont la valeur est contrôlée (x), et un axe vertical correspondant à la variable dépendante, ou à la variable dont la valeur est observée ou mesurée (y).
Lorsque la valeur de y change en fonction de x (c'est-à-dire que différentes valeurs de x correspondent à différentes valeurs de y), un graphique de cette variation peut être tracé ou esquissé. Le graphique peut être produit en utilisant des valeurs spécifiques pour des paires de données (x, y).
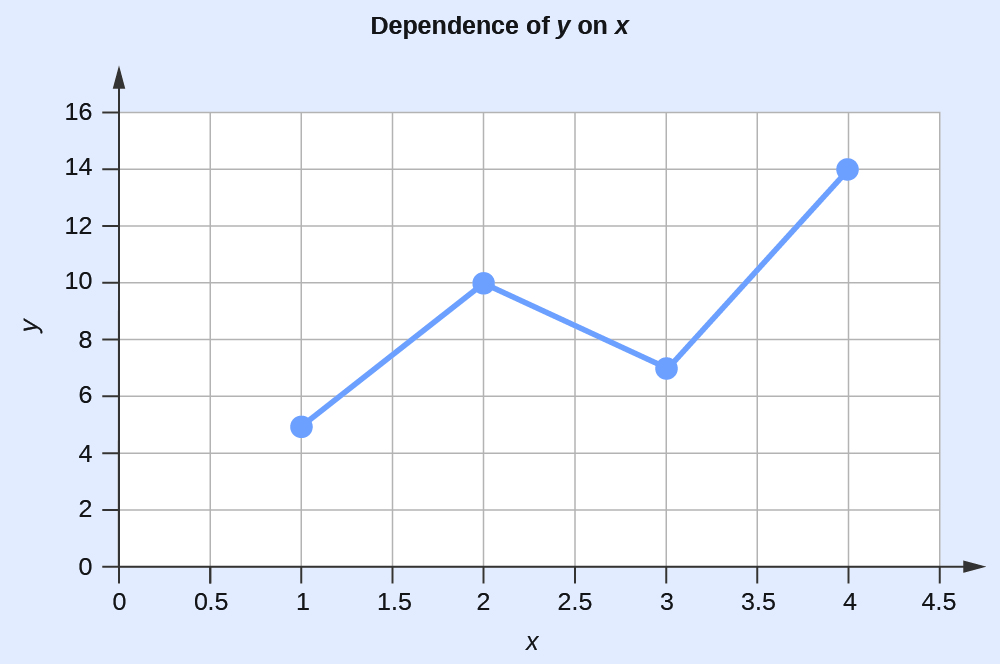
Représentation graphique de la dépendance de y par rapport à x
| x | y |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | 7 |
| 4 | 14 |
Ce tableau contient les points suivants : (1,5), (2,10), (3,7) et (4,14). Chacun de ces points peut être tracé sur un graphique et connecté pour produire une représentation graphique de la dépendance de y sur x.
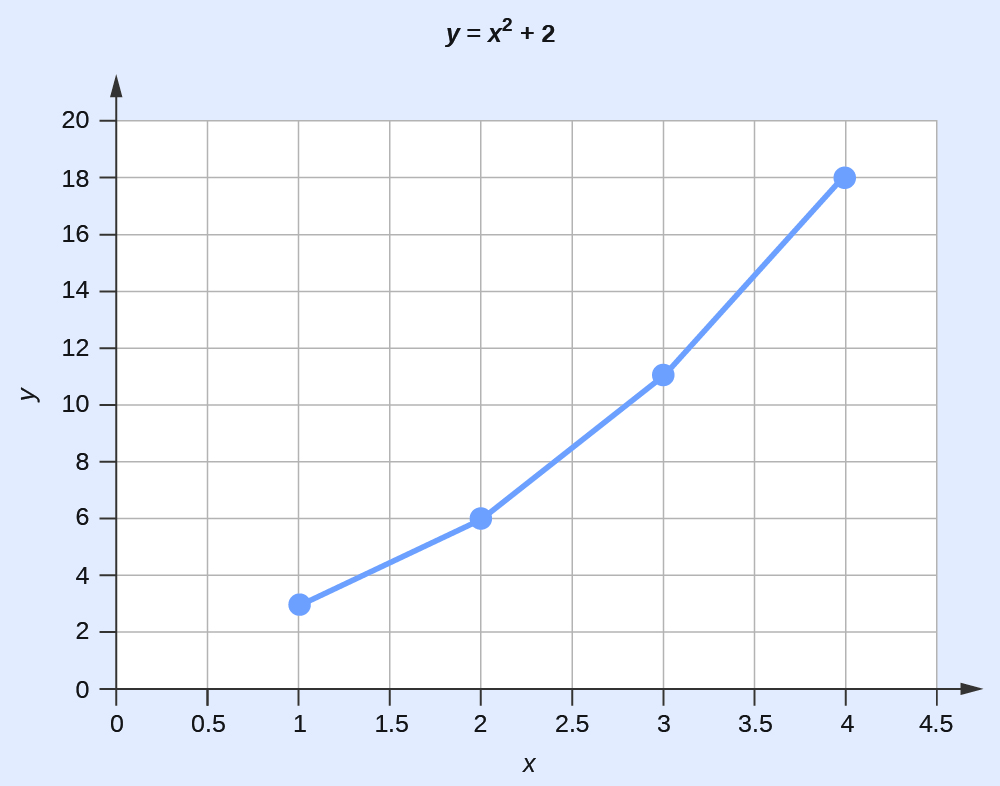
Si la fonction qui décrit la dépendance de y par rapport à x est connue, elle peut être utilisée pour calculer des paires de données x, y qui peuvent ensuite être tracées.
Plotting Data Pairs If we know that y = x2 + 2, we can produce a table of a few (x,y) values and then plot the line based on the data shown here.
| x | y = x2 + 2 |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 11 |
| 4 | 18 |