21.3 : Désintégration radioactive

Objectifs d'apprentissage

• Reconnaître les modes courants de désintégration radioactive
• Identifier les particules et les énergies communes impliquées dans les réactions de désintégration nucléaire
• Écrire et équilibrer des équations de désintégration nucléaire
• Calculer les paramètres cinétiques des processus de désintégration, y compris la demi-vie
• Décrire les techniques de datation radiométrique courantes

Suite à la découverte quelque peu fortuite de la radioactivité par Becquerel, de nombreux scientifiques éminents ont commencé à étudier ce nouveau phénomène intrigant. Parmi eux se trouvaient Marie Curie (la première femme à remporter un prix Nobel et la seule à avoir remporté deux prix Nobel dans différentes sciences, la chimie et la physique), qui a été la première à inventer le terme « radioactivité », et Ernest Rutherford (célèbre expérience sur la feuille d'or), qui a étudié et nommé trois des plus courants types de rayonnement. Au début du XXe siècle, de nombreuses substances radioactives ont été découvertes, les propriétés du rayonnement ont été étudiées et quantifiées, et une solide compréhension du rayonnement et de la désintégration nucléaire a été développée.

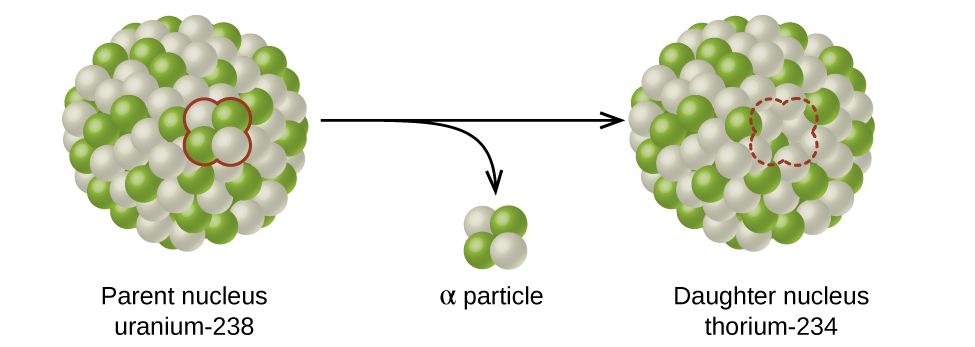
La transformation spontanée d'un nucléide instable en un autre est une désintégration radioactive. Le nucléide instable est appelé nucléide parent ; le nucléide résultant de la désintégration est connu sous le nom de nucléide fille. Le nucléide fille peut être stable ou se décomposer tout seul. Le rayonnement produit lors de la désintégration radioactive est tel que le nucléide fille se trouve plus près de la bande de stabilité que le nucléide parent, de sorte que la position d'un nucléide par rapport à la bande de stabilité peut servir de guide pour le type de désintégration qu'il subira (Figure\(\PageIndex{1}\)).

Figure\(\PageIndex{1}\) : Un noyau d'uranium 238 (le nucléide parent) subit une désintégration α pour former du thorium-234 (le nucléide fille). La particule alpha retire deux protons (vert) et deux neutrons (gris) du noyau d'uranium 238.

Un diagramme montre deux sphères composées de nombreuses petites sphères blanches et vertes reliées par une flèche orientée vers la droite et une autre flèche orientée vers le bas sortant de celle-ci. La sphère de gauche, intitulée « Nucleus parent uranium dash 238 », comporte deux sphères blanches et deux sphères vertes situées l'une à côté de l'autre et encadrées en rouge. Ces deux sphères vertes et deux sphères blanches apparaissent près de l'extrémité de la flèche orientée vers le bas et sont étiquetées « particule alpha ». La sphère de droite, intitulée « Daughter nucleus radon dash 234 », ressemble à la sphère de gauche, mais comporte un espace pour quatre sphères plus petites délimitées par une ligne pointillée rouge.

Bien que la désintégration radioactive d'un noyau soit trop petite pour être observée à l'œil nu, nous pouvons observer indirectement la désintégration radioactive dans un environnement appelé chambre à nuages. Cliquez ici pour en savoir plus sur les chambres à nuages et pour voir une démonstration intéressante de chambre à nuages réalisée par le Jefferson Lab.

Vidéo\(\PageIndex{1}\) : Comment construire une chambre à nuages !

Types de désintégration radioactive

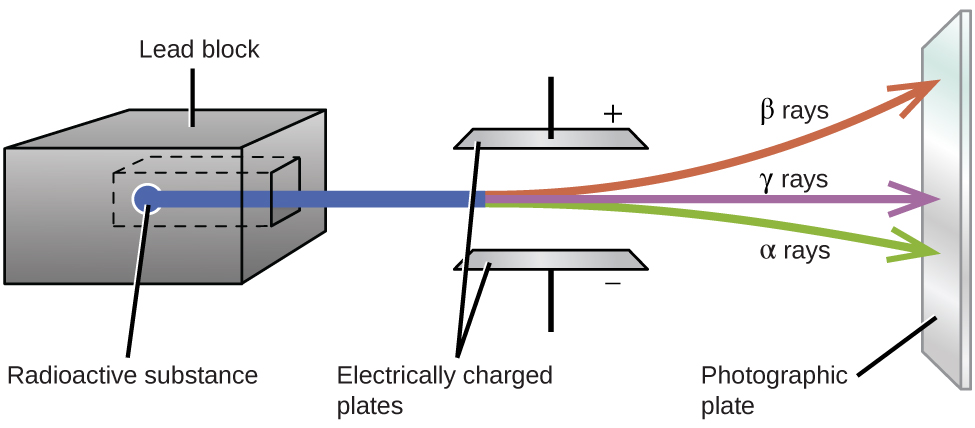
Les expériences d'Ernest Rutherford impliquant l'interaction du rayonnement avec un champ magnétique ou électrique (Figure\(\PageIndex{2}\)) l'ont aidé à déterminer qu'un type de rayonnement était constitué de\(α\) particules chargées positivement et relativement massives ; un second type était composé de particules chargées négativement et beaucoup moins \(β\)des particules massives ; et un troisième était constitué d'ondes électromagnétiques non chargées, de\(γ\) rayons. Nous savons maintenant que les\(α\) particules sont des noyaux d'hélium de haute énergie, que les\(β\) particules sont des électrons de haute énergie et que le\(γ\) rayonnement constitue un rayonnement électromagnétique de haute énergie. Nous classons différents types de désintégration radioactive en fonction du rayonnement produit.

Figure\(\PageIndex{2}\) : Les particules alpha, qui sont attirées par la plaque négative et déviées en quantité relativement faible, doivent être chargées positivement et relativement massives. Les particules bêta, qui sont attirées par la plaque positive et déviées en quantité relativement importante, doivent être chargées négativement et relativement légères. Les rayons gamma, qui ne sont pas affectés par le champ électrique, doivent être déchargés.

Un schéma est présenté. Une boîte grise sur le côté gauche du schéma intitulée « Bloc de plomb » comporte une chambre creusée au centre dans laquelle est placé un échantillon étiqueté « Substance radioactive ». Un faisceau bleu provient de l'échantillon, sort du bloc et traverse deux plaques placées horizontalement et étiquetées « plaques chargées électriquement ». La plaque supérieure est étiquetée par un signe positif tandis que la plaque inférieure est étiquetée par un signe négatif. On montre que le faisceau se divise en trois faisceaux lorsqu'il passe entre les plaques ; dans l'ordre, de haut en bas, ils sont rouges, étiquetés « rayons bêta », violets, « rayons gamma » et verts, « rayons alpha ». On montre que les faisceaux heurtent une plaque verticale étiquetée « Plaque photographique » à l'extrême droite du schéma.

Alpha (\(α\)) decayest l'émission d'une particule α par le noyau. Par exemple, le polonium-210 subit une désintégration α :

\[\ce{^{210}_{84}Po⟶ ^4_2He + ^{206}_{82}Pb} \hspace{40px}\ce{or}\hspace{40px} \ce{^{210}_{84}Po ⟶ ^4_2α + ^{206}_{82}Pb}\nonumber \]

La désintégration alpha se produit principalement dans les noyaux lourds (A > 200, Z > 83). Comme la perte d'une particule α donne un nucléide fille dont la masse est inférieure de quatre unités et dont le numéro atomique est inférieur de deux unités à celles du nucléide parent, le nucléide fille possède un rapport n:p plus élevé que le nucléide parent. Si le nucléide parent qui subit une désintégration α se trouve en dessous de la bande de stabilité, le nucléide fille se trouvera plus près de cette bande.

La désintégration bêta (β) est l'émission d'un électron par un noyau. L'iode 131 est un exemple de nucléide qui subit une désintégration β :

\[\ce{^{131}_{53}I ⟶ ^0_{-1}e + ^{131}_{54}X} \hspace{40px}\ce{or}\hspace{40px} \ce{^{131}_{53}I ⟶ ^0_{-1}β + ^{131}_{54}Xe}\nonumber \]

La désintégration bêta, qui peut être considérée comme la conversion d'un neutron en un proton et en une particule β, est observée dans les nucléides ayant un rapport n:p élevé. La particule bêta (électron) émise provient du noyau atomique et ne fait pas partie des électrons qui entourent le noyau. Ces noyaux se situent au-dessus de la bande de stabilité. L'émission d'un électron ne modifie pas le nombre de masse du nucléide mais augmente le nombre de ses protons et diminue le nombre de ses neutrons. Par conséquent, le rapport n:p diminue et le nucléide fille se trouve plus près de la bande de stabilité que le nucléide parent.

L'émission gamma (émission γ) est observée lorsqu'un nucléide se forme dans un état excité, puis se désintègre à son état fondamental avec l'émission d'un rayon γ, un quantum de rayonnement électromagnétique de haute énergie. La présence d'un noyau à l'état excité est souvent indiquée par un astérisque (*). Le cobalt 60 émet des radiations γ et est utilisé dans de nombreuses applications, y compris le traitement du cancer :

\[\mathrm{^{60}_{27}Co^* ⟶\, ^0_0γ +\, ^{60}_{27}Co}\nonumber \]

Il n'y a pas de changement du nombre de masse ou du numéro atomique lors de l'émission d'un rayon γ, sauf si l'émission γ accompagne l'un des autres modes de désintégration.

L'ion d'émission de positons (\(β^+\)désintégration) est l'émission d'un positron par le noyau. L'oxygène 15 est un exemple de nucléide soumis à une émission de positons :

\[\ce{^{15}_8O ⟶ ^0_{+1}e + ^{15}_7N} \hspace{40px}\ce{or}\hspace{40px} \ce{^{15}_8O ⟶ ^0_{+1}β + ^{15}_7N}\nonumber \]

L'émission de positons est observée pour les nucléides dans lesquels le rapport n:p est faible. Ces nucléides se situent en dessous de la bande de stabilité. La désintégration des positons est la conversion d'un proton en neutron lors de l'émission d'un positron. Le rapport n:p augmente et le nucléide fille se trouve plus près de la bande de stabilité que le nucléide parent.

La capture d'électrons se produit lorsque l'un des électrons internes d'un atome est capturé par le noyau de l'atome. Par exemple, le potassium 40 subit une capture d'électrons :

\[\ce{^{40}_{19}K + ^0_{-1}e ⟶ ^{40}_{18}Ar}\nonumber \]

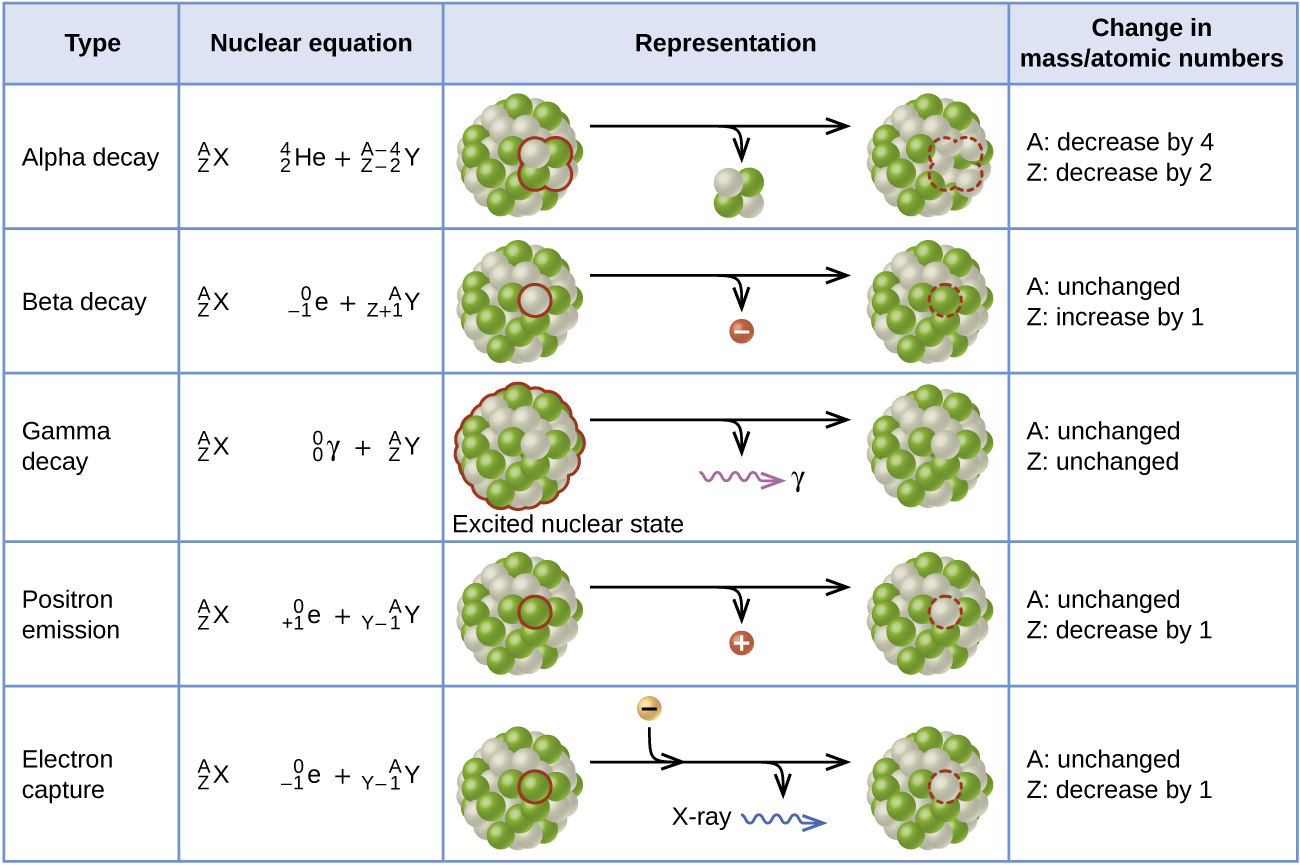
La capture d'électrons se produit lorsqu'un électron de la couche interne se combine à un proton et est converti en neutron. La perte d'un électron de la couche interne laisse un vide qui sera comblé par l'un des électrons extérieurs. Lorsque l'électron extérieur tombe dans le vide, il émet de l'énergie. Dans la plupart des cas, l'énergie émise se présentera sous forme de rayons X. Comme l'émission de positons, la capture d'électrons se produit pour les noyaux « riches en protons » situés en dessous de la bande de stabilité. La capture d'électrons a le même effet sur le noyau que l'émission de positons : le numéro atomique est diminué d'une unité et le nombre de masse ne change pas. Cela augmente le rapport n:p, et le nucléide fille se trouve plus près de la bande de stabilité que le nucléide parent. Il est difficile de prévoir s'il y a capture d'électrons ou émission de positons. Le choix est principalement dû à des facteurs cinétiques, celui qui nécessite la plus faible énergie d'activation étant celui qui a le plus de chances de se produire. La figure\(\PageIndex{3}\) résume ces types de désintégration, ainsi que leurs équations et leurs variations dans les nombres atomiques et de masse.

Figure\(\PageIndex{3}\) : Ce tableau résume le type, l'équation nucléaire, la représentation et tout changement de masse ou de nombre atomique pour différents types de désintégration.

Ce tableau comporte quatre colonnes et six rangées. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne : « Type », « Équation nucléaire », « Représentation » et « Modification de la masse/des nombres atomiques ». Dans la colonne « Type » se trouvent les éléments suivants : « Désintégration alpha », « Désintégration bêta », « Désintégration gamma », « Émission de positons » et « Capture d'électrons ». Dans la colonne « Équation nucléaire » se trouvent plusieurs équations. Chacune commence par l'exposant A empilé sur l'indice Z X. Il y a un grand espace, puis les équations suivantes : « exposant 4 empilé sur l'indice 2 Lui plus exposant A moins 4 empilés sur l'indice Z moins 2 Y », « exposant 0 empilé sur l'indice négatif 1 e plus exposant A empilé au-dessus de l'indice » indice Z plus 1 Y », « exposant 0 empilé sur l'indice 0 minuscule gamma plus exposant A empilé sur l'indice Z Y », « exposant 0 empilé sur l'indice positif 1 e plus exposant A empilé sur l'indice Y moins 1 Y » et « exposant 0 empilé sur l'indice négatif 1 e plus exposant A » empilé sur l'indice Y moins 1 Y. » Dans la colonne « Représentation » se trouvent les cinq diagrammes. La première montre un groupe de sphères vertes et blanches. Une section du cluster contenant deux sphères blanches et deux sphères vertes est délimitée. Une flèche orientée vers la droite pointe vers un groupe similaire à celui décrit précédemment, mais la section décrite est manquante. Une autre flèche part de la flèche et pointe vers le bas. Le petit groupe composé de deux sphères blanches et de deux sphères vertes apparaît à la fin de la flèche. Le diagramme suivant montre le même groupe de sphères blanches et vertes. Une sphère blanche est délimitée. Une flèche orientée vers la droite pointe vers un groupe similaire, mais la sphère blanche est absente. Une autre flèche part de la flèche principale et une sphère rouge avec un signe négatif apparaît à la fin. Le diagramme suivant montre le même groupe de sphères blanches et vertes. La sphère entière est délimitée et étiquetée « état nucléaire excité ». Une flèche orientée vers la droite pointe vers le même groupe. Aucune sphère ne manque. À côté de la flèche principale se trouve une autre flèche pointant vers une flèche gribouillée violette qui, à son tour, pointe vers un gamma minuscule. Le diagramme suivant montre le même groupe de sphères blanches et vertes. Une sphère verte est délimitée. Une flèche orientée vers la droite pointe vers un groupe similaire, mais la sphère verte est absente. Une autre flèche part de la flèche principale et une sphère rouge avec un signe positif apparaît à la fin. Le diagramme suivant montre le même groupe de sphères blanches et vertes. Une sphère verte est délimitée. Une flèche orientée vers la droite pointe vers un groupe similaire, mais la sphère verte est absente. Deux autres flèches partent de la flèche principale. La première montre une sphère dorée avec un signe négatif se joignant à la flèche orientée vers la droite. La seconde pointe vers une flèche bleue griffonnée « Radiographie ». Dans la colonne « Variation de la masse/du numéro atomique » se trouvent les éléments suivants : « A : diminution de 4, Z : diminution de 2 », « A : inchangé, Z : augmenté de 1 », « A : inchangé, Z : inchangé », « A : inchangé, Z : inchangé, Z : diminution de 1 » et « A : inchangé, Z : diminution de 1 ».

TEP scan

La tomographie par émission de positons (TEP) utilise les rayonnements pour diagnostiquer et suivre les problèmes de santé et surveiller les traitements médicaux en révélant le fonctionnement de certaines parties du corps d'un patient (Figure\(\PageIndex{4}\)). Pour effectuer une tomographie par émission de positrons, un radio-isotope émetteur de positons est produit dans un cyclotron, puis fixé à une substance utilisée par la partie du corps étudiée. Ce composé « étiqueté », ou radiotraceur, est ensuite introduit dans le patient (injecté par voie intraveineuse ou inhalé sous forme de gaz), et la façon dont il est utilisé par les tissus révèle le fonctionnement de cet organe ou de cette autre zone du corps.

Figure\(\PageIndex{4}\) : Un tomodensitomètre (a) utilise des radiations pour fournir une image du fonctionnement d'une partie du corps d'un patient. Les scans qu'il produit peuvent être utilisés pour imager un cerveau sain (b) ou peuvent être utilisés pour diagnostiquer des maladies telles que la maladie d'Alzheimer (c). (crédit a : modification d'une œuvre de Jens Maus)

Trois photos sont affichées et étiquetées « a », « b » et « c ». La figure a montre une machine à ouverture ronde connectée à une table d'examen. La photo b est un examen médical du haut de la tête d'une personne qui montre de grandes taches jaunes et rouges et de plus petites taches de bleu, de vert et de violet surlignées. La figure c montre également un scanner médical du haut de la tête d'une personne, mais cette image est principalement colorée en bleu et violet avec de très petites taches rouges et jaunes.

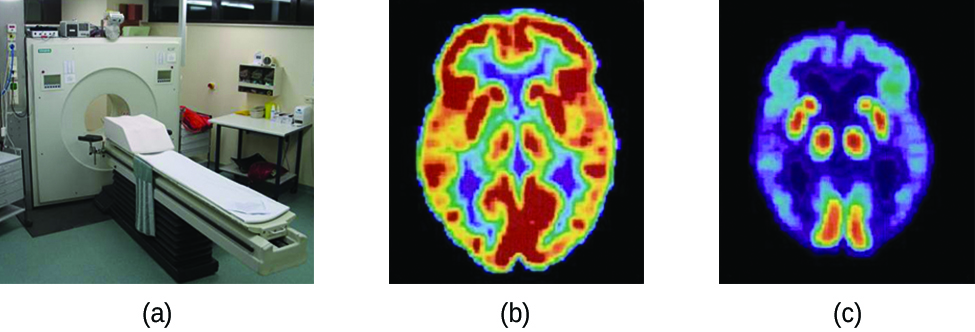
Par exemple, le F-18 est produit par bombardement protonique de ¹⁸ O\( (\ce{^{18}_8O + ^1_1p⟶ ^{18}_9F + ^1_0n})\) et incorporé dans un analogue du glucose appelé fludésoxyglucose (FDG). La façon dont l'organisme utilise le FDG fournit des informations diagnostiques essentielles ; par exemple, comme les cancers utilisent le glucose différemment des tissus normaux, le FDG peut révéler des cancers. Le ¹⁸ F émet des positrons qui interagissent avec les électrons voisins, produisant ainsi une rafale de rayonnement gamma. Cette énergie est détectée par le scanner et convertie en une image couleur détaillée en trois dimensions qui montre le fonctionnement de cette partie du corps du patient. Différents niveaux de rayonnement gamma produisent différentes quantités de luminosité et de couleurs dans l'image, qui peuvent ensuite être interprétées par un radiologue pour révéler ce qui se passe. La TEP permet de détecter les lésions cardiaques et les maladies cardiaques, d'aider à diagnostiquer la maladie d'Alzheimer, d'indiquer la partie du cerveau atteinte par l'épilepsie, de révéler le cancer, de montrer à quel stade il se trouve, dans quelle mesure il s'est propagé et si les traitements sont efficaces. Contrairement à l'imagerie par résonance magnétique et aux rayons X, qui ne font que montrer l'apparence d'une chose, le grand avantage de la TEP est qu'elle montre comment fonctionne une chose. Les tomodensitométries sont désormais généralement effectuées conjointement avec une tomodensitométrie.

Série de désintégration radioactive

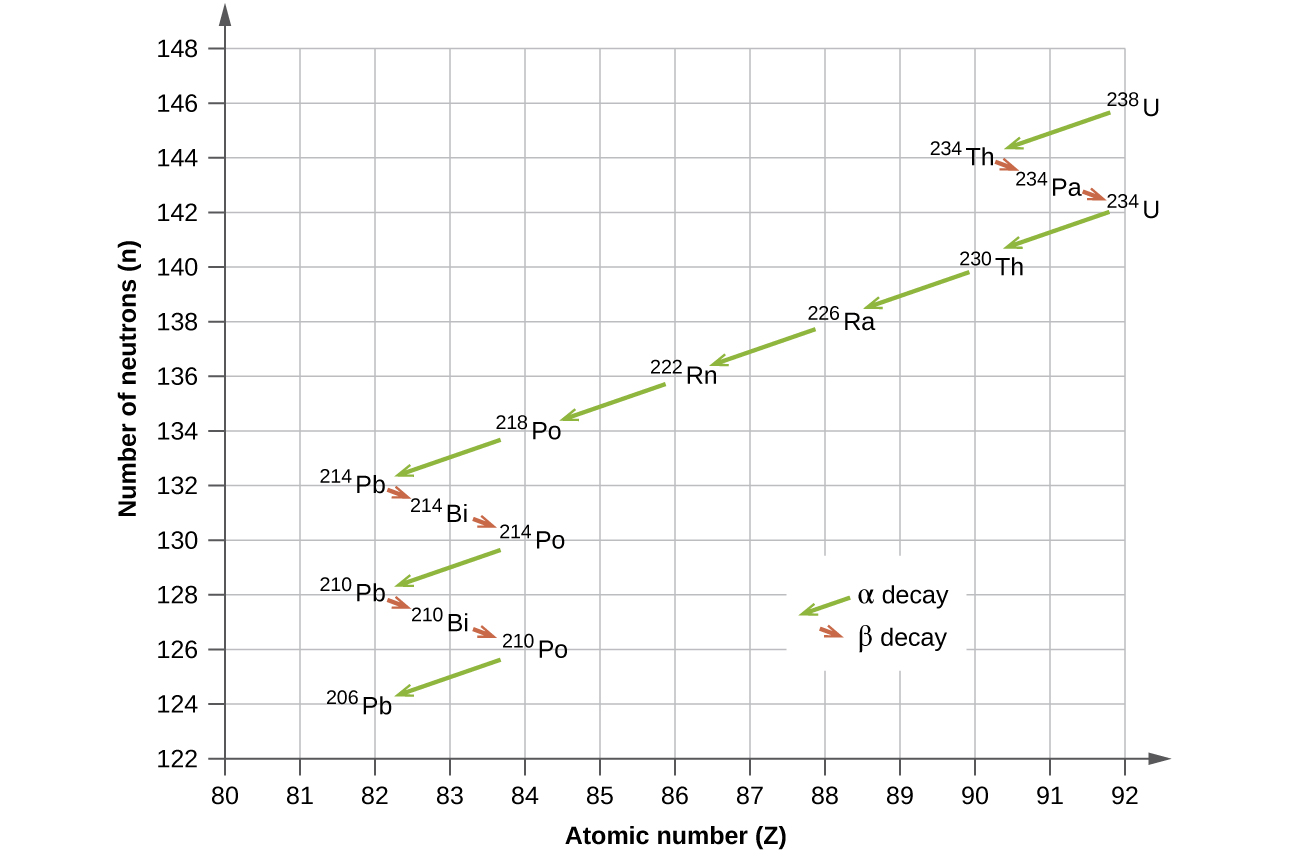
Les isotopes radioactifs naturels des éléments les plus lourds tombent en chaînes de désintégrations successives, ou désintégrations, et toutes les espèces d'une chaîne constituent une famille radioactive ou une série de désintégrations radioactives. Trois de ces séries incluent la plupart des éléments naturellement radioactifs du tableau périodique. Il s'agit de la série de l'uranium, de la série des actinides et de la série du thorium. La série du neptunium est une quatrième série, qui n'est plus significative sur Terre en raison de la courte demi-vie des espèces concernées. Chaque série est caractérisée par un parent (premier membre) qui a une longue demi-vie et une série de nucléides filles qui aboutissent finalement à un produit final stable, c'est-à-dire un nucléide sur la bande de stabilité (Figure\(\PageIndex{5}\)). Dans les trois séries, le produit final est un isotope stable du plomb. La série du neptunium, dont on pensait auparavant qu'elle se terminait par le bismuth-209, se termine par le thallium-205.

Figure\(\PageIndex{5}\) : L'uranium 238 subit une série de désintégration radioactive comprenant 14 étapes distinctes avant de produire du plomb 206 stable. Cette série comprend huit\(α\) désintégrations et six\(β\) désintégrations.

Un graphique est présenté où l'axe X est intitulé « Nombre de neutrons, parenthèses ouvertes, n, parenthèses fermées » et comporte des valeurs comprises entre 122 et 148 par incréments de 2. L'axe Y est intitulé « Numéro atomique » et possède des valeurs comprises entre 80 et 92 par incréments de 1. Deux types de flèches sont utilisés dans ce graphique pour relier les points. Les flèches vertes sont étiquetées comme « désintégration alpha » tandis que les flèches rouges sont étiquetées comme « désintégration bêta ». À partir du point « 92, 146 » étiqueté « exposant 238, U », une flèche verte relie ce point au deuxième point « 90, 144 » qui est étiqueté « exposant 234, T h ». Une flèche rouge le relie au troisième point « 91, 143 » qui est étiqueté « exposant 234, P a » qui est connecté au quatrième point « 92, 142 » par une flèche rouge et qui est étiqueté « exposant 234, U ». Une flèche verte mène au point suivant, « 90, 140 », qui est étiqueté « exposant 230, T h » et est relié par une flèche verte au sixième point, « 88, 138 » qui est étiqueté « exposant 226, R a » qui est à son tour connecté par une flèche verte au septième point « 86, 136 » qui est étiqueté « exposant 222, Ra ». Le huitième point, à « 84, 134 » est étiqueté « exposant 218, P o » et des flèches vertes y mènent et s'éloignent de celui-ci jusqu'au neuvième point « 82, 132 » qui est étiqueté « exposant 214, Pb » qui est relié par une flèche rouge au dixième point, « 83, 131 » qui est étiqueté « exposant 214, B i ». Une flèche rouge mène au onzième point « 84, 130 » étiqueté « exposant 214, P o » et une flèche verte mène au douzième point « 82, 128 » étiqueté « exposant 210, P b ». Une flèche rouge mène au treizième point « 83, 127 » étiqueté « exposant 210, B i » et une flèche rouge mène au quatorzième point « 84, 126 » étiqueté « exposant 210, P o ». Le dernier point est étiqueté « 82, 124 » et « exposant 206, P b ».

Demi-vies radioactives

La désintégration radioactive suit une cinétique de premier ordre. Comme les réactions de premier ordre ont déjà été abordées en détail dans le chapitre sur la cinétique, nous allons maintenant appliquer ces concepts aux réactions de désintégration nucléaire. Chaque nucléide radioactif possède une demi-vie constante caractéristique (t _1/2), soit le temps nécessaire à la désintégration de la moitié des atomes d'un échantillon. La demi-vie d'un isotope nous permet de déterminer pendant combien de temps un échantillon d'un isotope utile sera disponible et combien de temps un échantillon d'un isotope indésirable ou dangereux doit être conservé avant qu'il ne se désintègre à un niveau de rayonnement suffisamment faible pour ne plus poser de problème.

Par exemple, le cobalt-60, un isotope qui émet des rayons gamma utilisés pour traiter le cancer, a une demi-vie de 5,27 ans (Figure\(\PageIndex{6}\)). Dans une source donnée de cobalt 60, étant donné que la moitié des\(\ce{^{60}_{27}Co}\) noyaux se désintègrent tous les 5,27 ans, la quantité de matière et l'intensité du rayonnement émis sont réduites de moitié tous les 5,27 ans. (Notez que pour une substance donnée, l'intensité du rayonnement qu'elle produit est directement proportionnelle à la vitesse de désintégration de la substance et à la quantité de substance.) C'est ce que l'on peut attendre d'un procédé suivant une cinétique de premier ordre. Ainsi, une source de cobalt 60 utilisée pour le traitement du cancer doit être remplacée régulièrement pour continuer à être efficace.

Figure\(\PageIndex{6}\) : Pour le cobalt 60, dont la demi-vie est de 5,27 ans, 50 % subsistent après 5,27 ans (une demi-vie), 25 % restent après 10,54 ans (deux demi-vies), 12,5 % restent après 15,81 ans (trois demi-vies), etc.

Un graphique, intitulé « C o dash 60 Decay », est illustré où l'axe X est intitulé « C o tiret 60 restants, parenthèses ouvertes, signe de pourcentage, parenthèses fermantes » et comporte des valeurs comprises entre 0 et 100 par incréments de 25. L'axe Y est intitulé « Nombre de vies en demi-tiret » et possède des valeurs comprises entre 0 et 5 par incréments de 1. Le premier point, à « 0, 100 », comporte un cercle rempli de petits points tracés à proximité et étiquetés « 10 g ». Le deuxième point, à « 1, 50 », comporte un cercle plus petit rempli de petits points dessinés à proximité et étiquetés « 5 g ». Le troisième point, à « 2, 25 », comporte un petit cercle rempli de petits points dessinés à proximité et étiquetés « 2,5 g ». Le quatrième point, à « 3, 12,5 », comporte un tout petit cercle rempli de petits points dessinés à proximité et étiquetés « 1,25 g ». Le dernier point, à « 4, 6,35 », comporte un petit cercle rempli de petits points dessinés à proximité, étiquetés. » 625 g. »

Comme la désintégration nucléaire suit une cinétique de premier ordre, nous pouvons adapter les relations mathématiques utilisées pour les réactions chimiques de premier ordre. Nous substituons généralement le nombre de noyaux, N, à la concentration. Si le taux est exprimé en désintégrations nucléaires par seconde, nous l'appelons activité de l'échantillon radioactif. Le taux de désintégration radioactive est de :

\[\text{decay rate} = \lambda N\nonumber \]

avec\(\lambda\) est la constante de désintégration pour le radio-isotope en question.

La constante de désintégration\(\lambda\), qui est identique à une constante de vitesse décrite dans le chapitre sur la cinétique. Il est possible d'exprimer la constante de désintégration en termes de demi-vie, t _1/2 :

\[λ=\dfrac{\ln 2}{t_{1/2}}=\dfrac{0.693}{t_{1/2}} \hspace{40px}\ce{or}\hspace{40px} t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\nonumber \]

Les équations du premier ordre reliant la quantité, le N et le temps sont les suivantes :

\[N_t=N_0e^{−kt} \hspace{40px}\ce{or}\hspace{40px} t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\nonumber \]

où N ₀ est le nombre initial de noyaux ou de moles de l'isotope, et N _t est le nombre de nuclés/moles restants au temps t. L'exemple\(\PageIndex{1}\) applique ces calculs pour déterminer les taux de désintégration radioactive de nucléides spécifiques.

Exemple\(\PageIndex{1}\): Rates of Radioactive Decay

\(\ce{^{60}_{27}Co}\)se décompose avec une demi-vie de 5,27 ans à produire\(\ce{^{60}_{28}Ni}\).

1. Quelle est la constante de désintégration radioactive du cobalt-60 ?
2. Calculez la fraction d'un échantillon de l'\(\ce{^{60}_{27}Co}\)isotope qui restera après 15 ans.
3. Combien de temps faut-il pour qu'un échantillon\(\ce{^{60}_{27}Co}\) se désintègre au point qu'il ne reste que 2 % de la quantité initiale ?

Solution

a) La valeur de la constante de vitesse est donnée par :

\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{5.27\:y}=0.132\:y^{−1}} \nonumber \]

(b) La fraction restante après\(\ce{^{60}_{27}Co}\) que le temps t est donné par\(\dfrac{N_t}{N_0}\). En réorganisant la relation du premier ordre N _t = N ₀ e ^{— λt} pour résoudre ce rapport, on obtient :

\[\dfrac{N_t}{N_0}=e^{-λt}=e^\mathrm{-(0.132/y)(15.0/y)}=0.138 \nonumber \]

La fraction\(\ce{^{60}_{27}Co}\) qui restera après 15 ans est de 0,138. Autrement dit, 13,8 % des personnes\(\ce{^{60}_{27}Co}\) initialement présentes resteront après 15 ans.

(c) 2,00 % de la quantité initiale de\(\ce{^{60}_{27}Co}\) est égale à 0,0200 × N ₀. En substituant cela à l'équation du temps pour la cinétique du premier ordre, nous avons :

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)=−\dfrac{1}{0.132\:\ce y^{−1}}\ln\left(\dfrac{0.0200×N_0}{N_0}\right)=29.6\:\ce y \nonumber \]

Exercice\(\PageIndex{1}\)

Le radon 222\(\ce{^{222}_{86}Rn}\),, a une demi-vie de 3 823 jours. Combien de temps faudra-t-il à un échantillon de radon 222 d'une masse de 0,750 g pour se décomposer en d'autres éléments, ne laissant que 0,100 g de radon 222 ?

Réponse

11,1 jours

Comme chaque nucléide possède un nombre spécifique de nucléons, un équilibre particulier entre répulsion et attraction et son propre degré de stabilité, les demi-vies des nucléides radioactifs varient considérablement. Par exemple : la demi-vie de\(\ce{^{209}_{83}Bi}\) est de 1,9 × 10 ¹⁹ ans,\(\ce{^{239}_{94}Ra}\) de 24 000 ans,\(\ce{^{222}_{86}Rn}\) de 3,82 jours et de l'élément-111 (Rg pour le roentgenium) de 1,5 × 10 ^—3 secondes. Les demi-vies d'un certain nombre d'isotopes radioactifs importants pour la médecine sont présentées dans le tableau\(\PageIndex{1}\), et d'autres sont répertoriées à l'annexe N1.

Tableau\(\PageIndex{1}\) : Demi-vies des isotopes radioactifs importants pour la médecine

Type	Mode de désintégration	Demi-vie	Utilisations
F-18	β ^+ désintégration	110,0 minutes	tomodensitométrie
Co-60	désintégration β, désintégration γ	5,27 ans	traitement du cancer
TC-99m ^1	désintégration γ	8,01 heures	scintigraphies du cerveau, des poumons, du cœur et des os
I-131	désintégration β	8,02 jours	scintigraphie thyroïdienne et traitement
Tl-201	capture d'électrons	73 heures	scintigraphies du cœur et des artères ; tests de stress cardiaque
Le « m » dans Tc-99m signifie « métastable », ce qui indique qu'il s'agit d'un état instable à haute énergie du Tc-99. Les isotopes métastables émettent des\(γ\) radiations pour se débarrasser de l'excès d'énergie et devenir (plus) stables.

Datation radiométrique

Plusieurs radio-isotopes ont des demi-vies et d'autres propriétés qui les rendent utiles pour « dater » l'origine d'objets tels que des objets archéologiques, des organismes anciens vivants ou des formations géologiques. Ce processus est la datation radiométrique et a été à l'origine de nombreuses découvertes scientifiques révolutionnaires sur l'histoire géologique de la Terre, l'évolution de la vie et l'histoire de la civilisation humaine. Nous explorerons certains des types les plus courants de datation radioactive et comment les isotopes particuliers fonctionnent pour chaque type.

Datation radioactive à l'aide du carbone 14

La radioactivité du carbone 14 fournit une méthode pour dater les objets qui faisaient partie d'un organisme vivant. Cette méthode de datation radiométrique, également appelée datation au radiocarbone ou datation au carbone 14, est précise pour dater des substances contenant du carbone âgées de moins de 30 000 ans et peut fournir des dates raisonnablement précises jusqu'à un maximum d'environ 50 000 ans.

Le carbone naturel se compose de trois isotopes :\(\ce{^{12}_6C}\), qui constitue environ 99 % du carbone de la Terre ;\(\ce{^{13}_6C}\), environ 1 % du total ; et des traces de\(\ce{^{14}_6C}\). Le carbone 14 se forme dans la haute atmosphère par la réaction des atomes d'azote avec les neutrons émis par les rayons cosmiques de l'espace :

\[\ce{^{14}_7N + ^1_0n⟶ ^{14}_6C + ^1_1H}\nonumber \]

Tous les isotopes du carbone réagissent avec l'oxygène pour produire des molécules de CO ₂. Le rapport de\(\ce{^{14}_6CO2}\) à\(\ce{^{12}_6CO2}\) dépend du\(\ce{^{14}_6CO}\) rapport entre et\(\ce{^{12}_6CO}\) dans l'atmosphère. L'abondance naturelle\(\ce{^{14}_6CO}\) dans l'atmosphère est d'environ 1 partie par billion ; jusqu'à récemment, elle était généralement constante au fil du temps, comme en témoignent les échantillons de gaz trouvés piégés dans la glace. L'incorporation de plantes\(\ce{^{14}_6C ^{14}_6CO2}\) et\(\ce{^{12}_6CO2}\) dans celles-ci fait partie intégrante du processus de photosynthèse, ce qui signifie que le\(\ce{^{14}_6C: ^{12}_6C}\) rapport trouvé dans une plante vivante est le même que le\(\ce{^{14}_6C: ^{12}_6C}\) rapport dans l'atmosphère. Mais lorsque la plante meurt, elle ne piège plus le carbone par photosynthèse. Comme\(\ce{^{12}_6C}\) il s'agit d'un isotope stable qui ne subit pas de désintégration radioactive, sa concentration dans la plante ne change pas. Cependant, le carbone 14 se désintègre par émission β avec une demi-vie de 5 730 ans :

\[\ce{^{14}_6C⟶ ^{14}_7N + ^0_{-1}e}\nonumber \]

Ainsi, le\(\ce{^{14}_6C: ^{12}_6C}\) ratio diminue progressivement après la mort de la plante. La diminution du ratio avec le temps fournit une mesure du temps qui s'est écoulé depuis la mort de la plante (ou de tout autre organisme qui l'a mangée). La figure illustre\(\PageIndex{7}\) visuellement ce processus.

Figure\(\PageIndex{7}\) : Outre le carbone 12 stable, le carbone 14 radioactif est absorbé par les plantes et les animaux et y demeure à un niveau constant lorsqu'ils sont vivants. Après le décès, le C-14 se décompose et le ratio C-14:C-12 dans les restes diminue. La comparaison de ce ratio avec le rapport C-14:C-12 des organismes vivants nous permet de déterminer depuis combien de temps l'organisme a vécu (et est mort).

Un diagramme montre une vache debout sur le sol à côté d'un arbre. Dans le coin supérieur gauche du diagramme, où le ciel est représenté, une seule sphère blanche est représentée et est reliée par une flèche orientée vers le bas à une sphère plus grande composée de sphères vertes et blanches étiquetée « exposant 14, indice 7, N. ». Cette structure est reliée à trois autres structures par une flèche orientée vers la droite. Chacune des trois flèches pointant vers le sol est composée de sphères vertes et blanches. Le premier est intitulé « Trace, exposant 14, indice 6, C », le second est étiqueté « 1 pour cent, exposant 13, indice 6, C » et le dernier est étiqueté « 99 pour cent, exposant 12, indice 6, C ». Deux flèches orientées vers le bas qui se fondent en une seule flèche mènent de la vache et de l'arbre au sol et sont étiquetées « L'organisme meurt » et « exposant 14, indice 6, C, la décomposition commence ». Une flèche orientée vers la droite intitulée « Decay » en haut et « Time » en bas mène à l'étiquette « exposant 14, indice 6, C, barre oblique inverse, exposant 12, indice 6, C, indice 6, C, ratio diminué ». Près du sommet de l'arbre se trouve une flèche orientée vers le bas portant l'étiquette « exposant 14, indice 6, C, barre oblique inverse, exposant 12, indice 6, C, le ratio est constant dans les organismes vivants » qui mène à la dernière des affirmations inférieures.

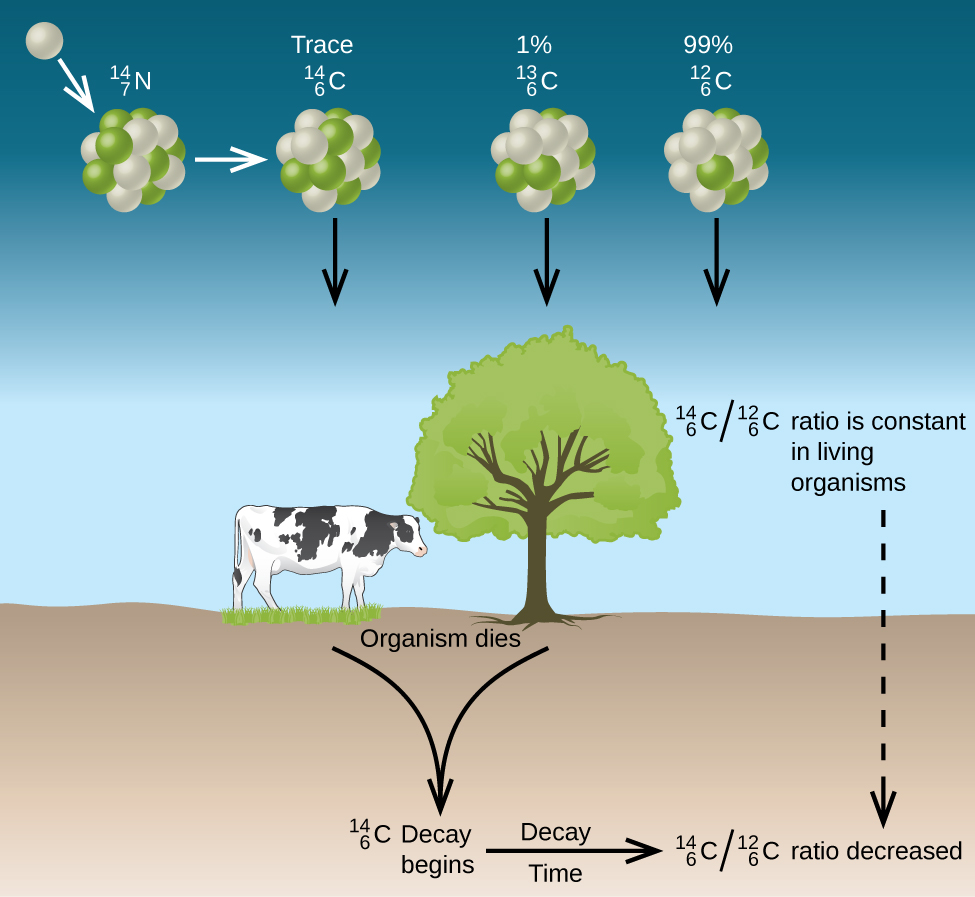
Par exemple, avec une demi-vie de 5\(\ce{^{14}_6C}\) 730 ans, si le\(\ce{^{14}_6C : ^{12}_6C}\) rapport entre un objet en bois découvert lors d'une fouille archéologique est la moitié de ce qu'il est dans un arbre vivant, cela indique que l'objet en bois a 5 730 ans. Des déterminations très précises des\(\ce{^{14}_6C : ^{12}_6C}\) ratios peuvent être obtenues à partir de très petits échantillons (aussi petits qu'un milligramme) à l'aide d'un spectromètre de masse.

Exemple\(\PageIndex{2}\): Radiocarbon Dating

Une minuscule feuille de papier (produite à partir de matière végétale autrefois vivante) extraite des manuscrits de la mer Morte a une activité de 10,8 désintégrations par minute et par gramme de carbone. Si l'activité initiale du C-14 était de 13,6 désintégrations/min/g de C, estimez l'âge des manuscrits de la mer Morte.

Solution

Le taux de désintégration (nombre de désintégrations/minute/gramme de carbone) étant proportionnel à la quantité de C-14 radioactif restant dans l'article, nous pouvons donc substituer les taux aux quantités, N, dans la relation suivante :

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)⟶t=−\dfrac{1}{λ}\ln\left(\dfrac{\ce{Rate}_t}{\ce{Rate}_0}\right) \nonumber \]

où l'indice 0 représente l'heure à laquelle les plantes ont été découpées pour fabriquer le papier, et l'indice t représente l'heure actuelle.

La constante de désintégration peut être déterminée à partir de la demi-vie du C-14, 5730 ans :

\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{5730\: y}=1.21×10^{−4}\:y^{−1}} \nonumber \]

En substituant et en résolvant, nous avons :

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{\ce{Rate}_t}{\ce{Rate}_0}\right)=\mathrm{−\dfrac{1}{1.21×10^{−4}\:y^{−1}}\ln\left(\dfrac{10.8\:dis/min/g\: C}{13.6\:dis/min/g\: C}\right)=1910\: y}\nonumber \]

Les manuscrits de la mer Morte datent donc d'environ 1900 ans (Figure\(\PageIndex{8}\)).

Figure\(\PageIndex{8}\) : La datation au carbone 14 a montré que ces pages des manuscrits de la mer Morte ont été écrites ou copiées sur du papier fabriqué à partir de plantes mortes entre 100 avant JC et 50 après JC.

Exercice\(\PageIndex{2}\)

Des dates plus précises des règnes des pharaons de l'Égypte ancienne ont été déterminées récemment à l'aide de plantes conservées dans leurs tombes. Des échantillons de graines et de matières végétales provenant de la tombe du roi Toutankhamon présentent un taux de décomposition C-14 de 9,07 désintégrations/min/g de C. Combien de temps le règne du roi Tut a-t-il pris fin ?

Réponse

il y a environ 3350 ans, soit environ 1340 av.

Des changements importants et bien documentés ont été apportés au\(\ce{^{14}_6C : ^{12}_6C}\) ratio. La précision d'une application simple de cette technique dépend du fait que le\(\ce{^{14}_6C : ^{12}_6C}\) ratio dans une plante vivante est le même aujourd'hui qu'il l'était à une époque antérieure, mais cela n'est pas toujours valable. En raison de l'accumulation croissante de molécules de CO ₂ (en grande partie\(\ce{^{12}_6CO2}\)) dans l'atmosphère causée par la combustion de combustibles fossiles (dans laquelle la quasi-totalité des molécules se sont désintégrées), le ratio de particules présentes\(\ce{^{14}_6C : ^{12}_6C}\) dans l'atmosphère\(\ce{^{14}_6C}\) est peut-être en train de changer. Cette augmentation de la présence\(\ce{^{12}_6CO2}\) dans l'atmosphère d'origine humaine entraîne une diminution du\(\ce{^{14}_6C : ^{12}_6C}\) ratio, ce qui affecte à son tour le ratio des organismes actuellement vivants sur Terre. Heureusement, nous pouvons toutefois utiliser d'autres données, telles que la datation des arbres par l'examen des anneaux de croissance annuels, pour calculer les facteurs de correction. Ces facteurs de correction permettent de déterminer des dates précises. En général, la datation radioactive ne fonctionne que pendant environ 10 demi-vies ; par conséquent, la limite pour la datation au carbone 14 est d'environ 57 000 ans.

Datation radioactive utilisant des nucléides autres que le carbone 14

La datation radioactive peut également utiliser d'autres nucléides radioactifs ayant des demi-vies plus longues pour dater des événements plus anciens. Par exemple, l'uranium 238 (qui se décompose en une série d'étapes en plomb-206) peut être utilisé pour établir l'âge des roches (et l'âge approximatif des roches les plus anciennes de la planète). Comme l'U-238 a une demi-vie de 4,5 milliards d'années, il faut autant de temps pour que la moitié de l'U-238 d'origine se désintègre en Pb-206. Dans un échantillon de roche ne contenant pas de quantités appréciables de Pb-208, l'isotope le plus abondant du plomb, nous pouvons supposer que le plomb n'était pas présent lorsque la roche s'est formée. Par conséquent, en mesurant et en analysant le ratio U-238 : Pb-206, nous pouvons déterminer l'âge de la roche. Cela suppose que tout le plomb-206 présent provient de la désintégration de l'uranium 238. Si du plomb 206 est présent, ce qui est indiqué par la présence d'autres isotopes du plomb dans l'échantillon, il est nécessaire de procéder à un ajustement. La datation au potassium-argon utilise une méthode similaire. Le K-40 se désintègre par émission de positrons et capture d'électrons pour former de l'Ar-40 avec une demi-vie de 1,25 milliard d'années. Si un échantillon de roche est concassé et que la quantité de gaz Ar-40 qui s'échappe est mesurée, la détermination du rapport Ar-40:K-40 donne l'âge de la roche. D'autres méthodes, comme la datation au rubidium-strontium (le Rb-87 se désintègre en Sr-87 avec une demi-vie de 48,8 milliards d'années), fonctionnent selon le même principe. Pour estimer la limite inférieure de l'âge de la Terre, les scientifiques déterminent l'âge de diverses roches et minéraux, en supposant que la Terre est plus ancienne que les roches et minéraux les plus anciens de sa croûte. En 2014, les plus anciennes roches connues sur Terre sont les zircones Jack Hills d'Australie, découverts par datation à l'uranium-plomb et âgés de près de 4,4 milliards d'années.

Exemple\(\PageIndex{3}\): Radioactive Dating of Rocks

Une roche ignée contient 9,58 × 10 ^—5 g d'U-238 et 2,51 × 10 ^—5 g de Pb-206, et des quantités beaucoup plus faibles de Pb-208. Déterminez l'heure approximative à laquelle la roche s'est formée.

Solution

L'échantillon de roche contient très peu de Pb-208, l'isotope le plus courant du plomb. Nous pouvons donc supposer que tout le Pb-206 de la roche a été produit par la désintégration radioactive de l'U-238. Lorsque la roche s'est formée, elle contenait tout l'U-238 qui s'y trouvait actuellement, ainsi qu'une partie de l'U-238 qui a depuis subi une désintégration radioactive.

La quantité d'U-238 actuellement présente dans la roche est de :

\[\mathrm{9.58×10^{−5}\cancel{g\: U}×\left( \dfrac{1\: mol\: U}{238\cancel{g\: U}}\right )=4.03×10^{−7}\:mol\: U}\nonumber \]

Parce que lorsqu'une mole d'U-238 se désintègre, elle produit une mole de Pb-206, la quantité d'U-238 qui a subi une désintégration radioactive depuis la formation de la roche est la suivante :

\[\mathrm{2.51×10^{-5}\cancel{g\: Pb}×\left( \dfrac{1\cancel{mol\: Pb}}{206\cancel{g\: Pb}}\right )×\left(\dfrac{1\: mol\: U}{1\cancel{mol\: Pb}}\right)=1.22×10^{-7}\:mol\: U}\nonumber \]

La quantité totale d'U-238 initialement présente dans la roche est donc de :

\[\mathrm{4.03×10^{−7}\:mol+1.22×10^{−7}\:mol=5.25×10^{−7}\:mol\: U}\nonumber \]

Le temps qui s'est écoulé depuis la formation de la roche est donné par :

\[t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\nonumber \]

avec N ₀ représentant la quantité initiale d'U 238 et N _t représentant la quantité actuelle d'U 238.

L'U-238 se désintègre en Pb-206 avec une demi-vie de 4,5 × 10 ⁹ y, donc la constante de désintégration λ est la suivante :

\[λ=\dfrac{\ln 2}{t_{1/2}}=\mathrm{\dfrac{0.693}{4.5×10^9\:y}=1.54×10^{−10}\:y^{−1}}\nonumber \]

En substituant et en résolvant, nous avons :

\[t=\mathrm{−\dfrac{1}{1.54×10^{−10}\:y^{−1}}\ln\left(\dfrac{4.03×10^{−7}\cancel{mol\: U}}{5.25×10^{−7}\cancel{mol\: U}}\right)=1.7×10^9\:y}\nonumber \]

La roche a donc environ 1,7 milliard d'années.

Exercice\(\PageIndex{3}\)

Un échantillon de roche contient 6,14 × 10 ^—4 g de Rb-87 et 3,51 × 10 ^—5 g de Sr-87. Calculez l'âge de la roche. (La demi-vie de la désintégration β du Rb-87 est de 4,7 × 10 ¹⁰ ans.)

Réponse

3,7 × 10 x ⁹ ans

Résumé

Les noyaux dont le rapport n:p est instable subissent une désintégration radioactive spontanée. Les types de radioactivité les plus courants sont la désintégration α, la désintégration β, l'émission γ, l'émission de positons et la capture d'électrons. Les réactions nucléaires impliquent également souvent des rayons γ, et certains noyaux se désintègrent par capture d'électrons. Chacun de ces modes de désintégration conduit à la formation d'un nouveau noyau avec un rapport n:p plus stable. Certaines substances subissent une série de désintégration radioactive, qui se désintègre de multiples fois avant de se terminer par un isotope stable. Tous les processus de désintégration nucléaire suivent une cinétique de premier ordre, et chaque radio-isotope possède sa propre demi-vie caractéristique, c'est-à-dire le temps nécessaire à la désintégration de la moitié de ses atomes. En raison des grandes différences de stabilité entre les nucléides, les demi-vies des substances radioactives sont très variées. Nombre de ces substances ont trouvé des applications utiles dans le diagnostic et le traitement médicaux, la détermination de l'âge des objets archéologiques et géologiques, etc.

Équations clés

• taux de désintégration = λN
• \(t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\)

Lexique

désintégration alpha (α)

perte d'une particule alpha lors de la désintégration radioactive

désintégration bêta (β)

décomposition d'un neutron en un proton, qui reste dans le noyau, et en un électron, qui est émis sous forme de particule bêta

nucléide fille

nucléide produit par la désintégration radioactive d'un autre nucléide ; peut être stable ou peut se désintégrer davantage

capture d'électrons

combinaison d'un électron central et d'un proton pour produire un neutron dans le noyau

émission gamma (γ)

désintégration d'un nucléide à l'état excité accompagnée de l'émission d'un rayon gamma

demi-vie (t _1/2)

temps nécessaire à la désintégration de la moitié des atomes d'un échantillon radioactif

nucléide parent

nucléide instable qui se transforme spontanément en un autre nucléide (fille)

émission de positons

(également, désintégration β ⁺) conversion d'un proton en neutron, qui reste dans le noyau, et en positron, qui est émis

désintégration radioactive

désintégration spontanée d'un nucléide instable en un autre nucléide

série de désintégration radioactive

des chaînes de désintégrations successives (désintégrations radioactives) qui aboutissent finalement à un produit final stable

datation au radiocarbone

des moyens très précis de dater des objets âgés de 30 000 à 50 000 ans dérivés de matière autrefois vivante ; obtenu\(\ce{^{14}_6C : ^{12}_6C}\) en calculant le rapport entre l'intérieur de l'objet et le ratio de\(\ce{^{14}_6C : ^{12}_6C}\) l'atmosphère actuelle

datation radiométrique

utilisation de radio-isotopes et de leurs propriétés pour dater la formation d'objets tels que des artefacts archéologiques, des organismes anciens vivants ou des formations géologiques