21.1 : Structure et stabilité nucléaires
- Page ID
- 194027
- Décrire la structure nucléaire en termes de protons, de neutrons et d'électrons
- Calculer le défaut de masse et l'énergie de liaison pour les noyaux
- Expliquer les tendances de la stabilité relative des noyaux
La chimie nucléaire est l'étude des réactions qui impliquent des modifications de la structure nucléaire. Le chapitre sur les atomes, les molécules et les ions a introduit l'idée de base de la structure nucléaire, selon laquelle le noyau d'un atome est composé de protons et, à l'exception de\(\ce{^1_1H}\) neutrons. Rappelons que le nombre de protons dans le noyau est appelé numéro atomique (\(Z\)) de l'élément, et que la somme du nombre de protons et du nombre de neutrons est le nombre de masse (\(A\)). Les atomes ayant le même numéro atomique mais des numéros de masse différents sont des isotopes du même élément. Lorsque nous faisons référence à un seul type de noyau, nous utilisons souvent le terme nucléide et l'identifions par la notation suivante :
\[\ce{^{A}_{Z}X} \label{Eq1} \]
où
- \(X\)est le symbole de l'élément,
- \(A\)est le nombre de masse, et
- \(Z\)est le numéro atomique.
Un nucléide est souvent référencé par le nom de l'élément suivi d'un trait d'union et du numéro de masse. Par exemple,\(\ce{^{14}_6C}\) est appelé « carbone 14 ».
Les protons et les neutrons, collectivement appelés nucléons, sont étroitement liés les uns aux autres dans un noyau. Avec un rayon d'environ 10 -15 mètres, un noyau est assez petit par rapport au rayon de l'atome entier, qui est d'environ 10 -10 mètres. Les noyaux sont extrêmement denses par rapport à la matière en vrac, avec une moyenne de\(1.8 \times 10^{14}\) grammes par centimètre cube. Par exemple, l'eau a une densité de 1 gramme par centimètre cube et l'iridium, l'un des éléments les plus denses connus, a une densité de 22,6 g/cm 3. Si la densité de la Terre était égale à la densité nucléaire moyenne, le rayon de la Terre ne serait que d'environ 200 mètres (le rayon réel de la Terre est d'environ\(6.4 \times 10^6\) mètres, 30 000 fois plus grand). \(\PageIndex{1}\)L'exemple montre à quel point les densités nucléaires peuvent être importantes dans le monde naturel.
Densité d'une étoile à neutrons Les étoiles à neutrons se forment lorsque le cœur d'une étoile très massive subit un effondrement gravitationnel, provoquant l'explosion des couches extérieures de l'étoile en supernova. Composées presque entièrement de neutrons, ce sont les étoiles les plus denses connues de l'univers, avec des densités comparables à la densité moyenne d'un noyau atomique. Une étoile à neutrons dans une galaxie lointaine a une masse égale à 2,4 masses solaires (1 masse solaire\(M_☉\) = = masse du soleil =\(\mathrm{1.99 \times 10^{30}\; kg}\)) et un diamètre de 26 km.
- Quelle est la densité\(\rho\) de cette étoile à neutrons ?
- Comment la densité de cette étoile à neutrons se compare-t-elle à celle d'un noyau d'uranium, dont le diamètre est d'environ 15 fm (1 fm = 10 —15 m) ?
Solution
Nous pouvons traiter à la fois l'étoile à neutrons et le noyau U-235 comme des sphères. Ensuite, la densité pour les deux est donnée par :
\[\rho = \dfrac{m}{V} \nonumber \]
avec
\[V = \dfrac{4}{3} \pi r^3 \nonumber \]
(a) Le rayon de l'étoile à neutrons est\(\mathrm{\dfrac{1}{2}\times 26\; km = \dfrac{1}{2} \times 2.6 \times 10^4\; m = 1.3 \times 10^4\; m}\) tel que la densité de l'étoile à neutrons est :
\[ \begin{align*} \rho &= \dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{2.4(1.99 \times 10^{30}\;kg)}{\frac{4}{3} \pi (1.3 \times 10^4m)^3} \\[4pt] &=5.2 \times 10^{17}\;kg/m^3 \end{align*} \nonumber \]
(b) Le rayon du noyau U-235 est\(\mathrm{\dfrac{1}{2} \times 15 \times 10^{−15}\;m=7.5 \times 10^{−15}\;m}\) de sorte que la densité du noyau U-235 est de :
\[ \begin{align*} \rho &=\dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{235\;amu \left(\frac{1.66 \times 10^{-27}\;kg}{1\;amu}\right)}{ \frac{4}{3} \pi (7.5 \times 10^{-15}m)^3} \\[4pt] &=2.2 \times 10^{17} \; kg/m^3 \end{align*} \nonumber \]
Ces valeurs sont assez similaires (même ordre de grandeur), mais le noyau est plus de deux fois plus dense que l'étoile à neutrons.
Déterminez la densité d'une étoile à neutrons d'une masse de 1,97 masse solaire et d'un diamètre de 13 km, et comparez-la à la densité d'un noyau d'hydrogène, qui a un diamètre de 1,75 fm (\(\mathrm{1\; fm = 1 \times 10^{–15}\; m}\)).
- Réponse
-
La densité de l'étoile à neutrons est de\(\mathrm{3.4 \times 10^{18}\; kg/m^3}\). La densité d'un noyau d'hydrogène est de\(\mathrm{6.0 \times 10^{17}\; kg/m^3}\). L'étoile à neutrons est 5,7 fois plus dense que le noyau d'hydrogène.
Pour maintenir ensemble des protons chargés positivement dans le très petit volume d'un noyau, il faut des forces d'attraction très fortes, car les protons chargés positivement se repoussent fortement les uns les autres sur de si courtes distances. La force d'attraction qui maintient le noyau ensemble est la force nucléaire puissante. (La force forte est l'une des quatre forces fondamentales dont l'existence est connue. Les autres sont la force électromagnétique, la force gravitationnelle et la force nucléaire faible.) Cette force agit entre les protons, entre les neutrons et entre les protons et les neutrons. Elle est très différente de la force électrostatique qui maintient les électrons chargés négativement autour d'un noyau chargé positivement (l'attraction entre des charges opposées). Sur des distances inférieures à 10 -15 mètres et à l'intérieur du noyau, la force nucléaire puissante est beaucoup plus forte que les répulsions électrostatiques entre protons ; sur de plus grandes distances et à l'extérieur du noyau, elle est pratiquement inexistante.
Énergie nucléaire contraignante
À titre d'exemple simple de l'énergie associée à la forte force nucléaire, considérez l'atome d'hélium composé de deux protons, de deux neutrons et de deux électrons. La masse totale de ces six particules subatomiques peut être calculée comme suit :
\[ \underset{\Large\text{protons}}{(2 \times 1.0073\; \text{amu})} + \underset{\Large\text{neutrons}}{(2 \times 1.0087\; \text{amu})} + \underset{\Large\text{electrons}}{(2 \times 0.00055\; \text{amu})}= 4.0331\; \text{amu }\label{Eq2} \]
Cependant, les mesures par spectrométrie de masse révèlent que la masse d'un\(\ce{_2^4 He}\) atome est de 4 0026 amu, soit moins que les masses combinées des six particules subatomiques qui le constituent. Cette différence entre les masses calculées et mesurées expérimentalement est connue sous le nom de défaut de masse de l'atome. Dans le cas de l'hélium, le défaut de masse indique une « perte » de masse de 4,0331 amu — 4,0026 amu = 0,0305 amu. La perte de masse qui accompagne la formation d'un atome à partir de protons, de neutrons et d'électrons est due à la conversion de cette masse en énergie qui se dégage au fur et à mesure de la formation de l'atome. L'énergie de liaison nucléaire est l'énergie produite lorsque les nucléons des atomes sont liés entre eux ; c'est également l'énergie nécessaire pour décomposer un noyau en protons et neutrons qui le constituent. Par rapport aux énergies de liaison chimique, les énergies de liaison nucléaire sont beaucoup plus élevées, comme nous l'apprendrons dans cette section. Par conséquent, les changements d'énergie associés aux réactions nucléaires sont beaucoup plus importants que ceux des réactions chimiques.
La conversion entre masse et énergie est représentée de manière plus identifiable par l'équation d'équivalence masse-énergie énoncée par Albert Einstein :
\[E=mc^2 \label{Eq3} \]
où E est l'énergie, m est la masse de la matière à convertir et c est la vitesse de la lumière dans le vide. Cette équation peut être utilisée pour déterminer la quantité d'énergie qui résulte de la conversion de la matière en énergie. À l'aide de cette équation d'équivalence masse-énergie, l'énergie de liaison nucléaire d'un noyau peut être calculée à partir de son défaut de masse, comme le montre l'exemple\(\PageIndex{2}\). Diverses unités sont couramment utilisées pour les énergies de liaison nucléaire, y compris les électronvolts (eV), 1 eV étant égal à la quantité d'énergie nécessaire pour déplacer la charge d'un électron sur une différence de potentiel électrique de 1 volt, faisant\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\).
Déterminer l'énergie de liaison du nucléide\(\ce{^4_2 He}\) dans :
- joules par mole de noyaux
- joules par noyau
- MeV par noyau
Solution
Le défaut de masse d'un\(\ce{^4_2He}\) noyau est de 0,0305 amu, comme indiqué précédemment. Déterminez l'énergie de liaison en joules par nucléide à l'aide de l'équation d'équivalence masse-énergie. Pour prendre en compte les unités d'énergie demandées, le défaut de masse doit être exprimé en kilogrammes (rappelons que 1 J = 1 kg m 2 /s 2).
a) Tout d'abord, exprimer le défaut de masse en g/mol. Cela se fait facilement compte tenu de l'équivalence numérique de la masse atomique (amu) et de la masse molaire (g/mol) qui résulte des définitions des unités amu et molaire (voir la discussion précédente dans le chapitre sur les atomes, les molécules et les ions si nécessaire). Le défaut de masse est donc de 0,0305 g/mol. Pour prendre en compte les unités des autres termes de l'équation masse-énergie, la masse doit être exprimée en kg, puisque 1 J = 1 kg m 2 /s 2. La conversion de grammes en kilogrammes donne un défaut de masse de\(\mathrm{3.05 \times 10^{–5}\; kg/mol}\). En substituant cette quantité à l'équation d'équivalence masse-énergie, on obtient :
\[\begin{align*} E &=mc^2 \\[4pt] &= \dfrac{3.05 \times 10^{-5}\;kg}{mol} \times \left(\dfrac{2.998 \times 10^8\;m}{s}\right)^2 \\[4pt] &= 2.74×10^{12}\:kg\:m^2s^{-2}mol^{-1} \\[4pt] &=2.74 \times 10^{12}\;J/mol=2.74\: TJ /mol \end{align*} \nonumber \]
(b) L'énergie de liaison pour un noyau unique est calculée à partir de l'énergie de liaison molaire en utilisant le nombre d'Avogadro :
\[\begin{align*} E &= 2.74×10^{12}\:J\:mol^{-1}×\dfrac{1\: mol}{6.022×10^{23}\:nuclei} \\[4pt] &=4.55×10^{-12} \: J =4.55\: pJ \end{align*} \nonumber \]
(c) Rappelez-vous que\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\). En utilisant l'énergie de liaison calculée dans la partie (b) :
\[\begin{align*} E &= 4.55×10^{-12} \: J× \dfrac{1\: eV}{1.602×10^{-19}\:J} \\[4pt] &=2.84×10^7\:eV=28.4\: MeV \end{align*} \nonumber \]
Quelle est l'énergie de liaison du nucléide\(\ce{^{19}_9F}\) (masse atomique : 18,9984 amu) en MeV par noyau ?
- Réponse
-
148,4 MeV
Comme les changements d'énergie liés à la rupture et à la formation de liaisons sont si faibles par rapport aux changements d'énergie liés à la rupture ou à la formation de noyaux, les changements de masse lors de toutes les réactions chimiques ordinaires sont pratiquement indétectables. Comme décrit dans le chapitre sur la thermochimie, les réactions chimiques les plus énergétiques présentent des enthalpies de l'ordre de milliers de kJ/mol, ce qui équivaut à des différences de masse de l'ordre du nanogramme (10 à 9 g). D'autre part, les énergies de liaison nucléaire sont généralement de l'ordre de milliards de kJ/mol, ce qui correspond à des différences de masse de l'ordre du milligramme (10 à 3 g).
Stabilité nucléaire
Un noyau est stable s'il ne peut pas être transformé dans une autre configuration sans apport d'énergie provenant de l'extérieur. Parmi les milliers de nucléides existants, environ 250 sont stables. Un diagramme du nombre de neutrons par rapport au nombre de protons pour les noyaux stables révèle que les isotopes stables se situent dans une bande étroite. Cette région est connue sous le nom de bande de stabilité (également appelée ceinture, zone ou vallée de stabilité). La ligne droite de la figure\(\PageIndex{1}\) représente les noyaux qui ont un rapport de 1:1 entre les protons et les neutrons (rapport n:p). Notez que les noyaux stables plus légers contiennent en général le même nombre de protons et de neutrons. Par exemple, l'azote 14 possède sept protons et sept neutrons. Les noyaux stables plus lourds contiennent toutefois de plus en plus de neutrons que de protons. Par exemple : le fer-56 possède 30 neutrons et 26 protons, soit un rapport n:p de 1,15, tandis que le nucléide stable plomb-207 possède 125 neutrons et 82 protons, soit un rapport n:p égal à 1,52. Cela est dû au fait que les noyaux plus gros ont plus de répulsions proton-proton et ont besoin d'un plus grand nombre de neutrons pour fournir des forces fortes de compensation permettant de surmonter ces répulsions électrostatiques et de maintenir le noyau uni.
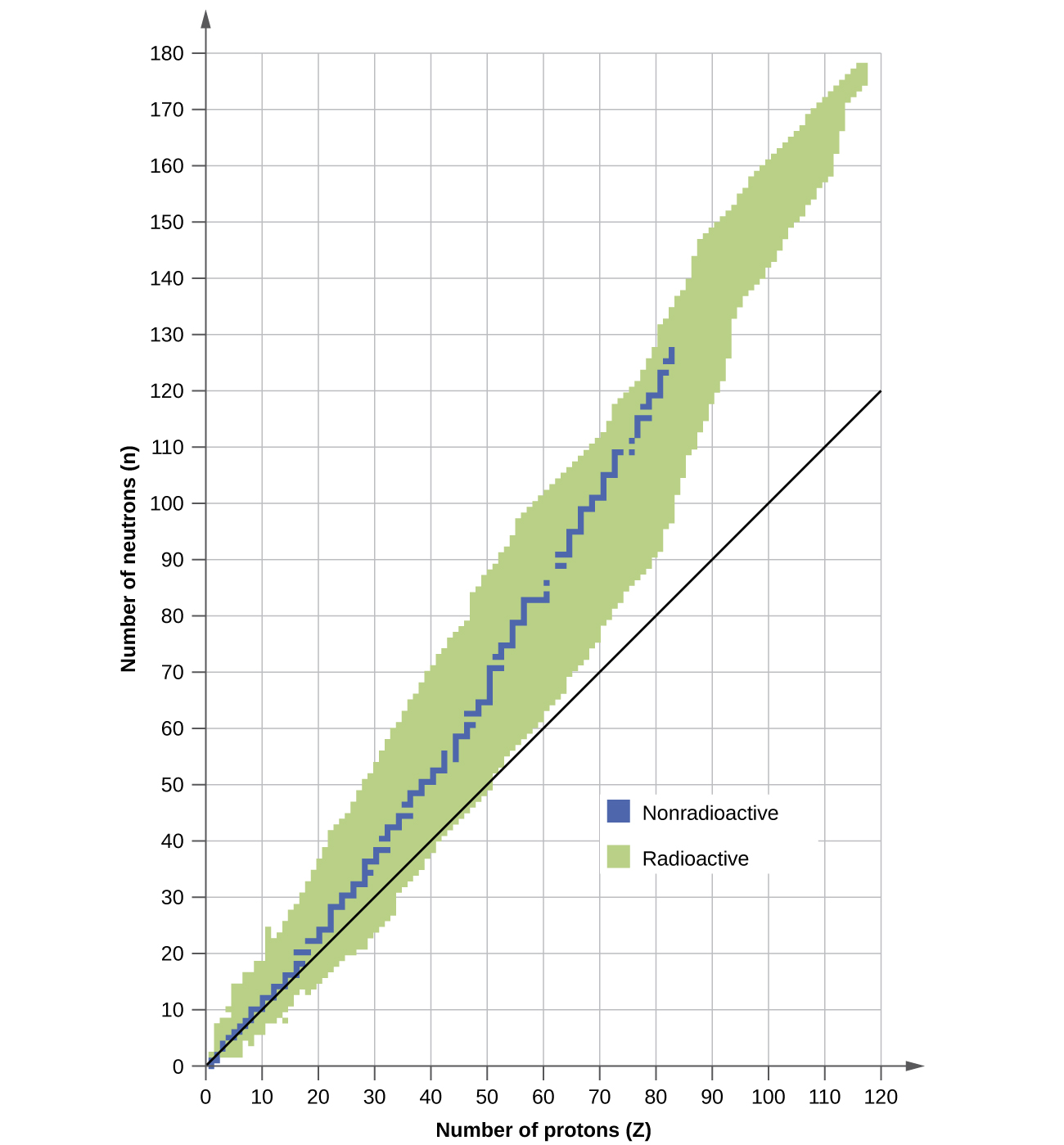
Les noyaux situés à gauche ou à droite de la bande de stabilité sont instables et présentent de la radioactivité. Ils se transforment spontanément (désintégration) en d'autres noyaux situés soit dans la bande de stabilité, soit plus proches de celle-ci. Ces réactions de désintégration nucléaire convertissent un isotope instable (ou radio-isotope) en un autre isotope plus stable. Nous aborderons la nature et les produits de cette désintégration radioactive dans les sections suivantes de ce chapitre.
Plusieurs observations peuvent être faites concernant la relation entre la stabilité d'un noyau et sa structure. Les noyaux contenant un nombre pair de protons, de neutrons ou les deux sont plus susceptibles d'être stables (Tableau\(\PageIndex{1}\)). Les noyaux contenant un certain nombre de nucléons, appelés nombres magiques, sont stables contre la désintégration nucléaire. Ces nombres de protons ou de neutrons (2, 8, 20, 28, 50, 82 et 126) forment des coquilles complètes dans le noyau. Leur concept est similaire à celui des couches d'électrons stables observées pour les gaz rares. Les noyaux qui ont des nombres magiques de protons et de neutrons\(\ce{^4_2He}\), tels que\(\ce{^{16}_8O}\)\(\ce{^{40}_{20}Ca}\),,\(\ce{^{208}_{82}Pb}\) et sont particulièrement stables. Ces tendances en matière de stabilité nucléaire peuvent être rationalisées en considérant un modèle mécanique quantique des états de l'énergie nucléaire analogue à celui utilisé pour décrire les états électroniques plus haut dans ce manuel. Les détails de ce modèle dépassent le cadre de ce chapitre.
| Nombre d'isotopes stables | Nombre de protons | Nombre de neutrons |
|---|---|---|
| 157 | même | même |
| 53 | même | impair |
| 50 | impair | même |
| 5 | impair | impair |
La stabilité relative d'un noyau est corrélée à son énergie de liaison par nucléon, c'est-à-dire l'énergie de liaison totale du noyau divisée par le nombre de nucléons du noyau. Par exemple, l'énergie de liaison d'un\(\ce{^4_2He}\) noyau est donc :
\[\mathrm{\dfrac{28.4\; MeV}{4\; nucleons}=7.10\; MeV/nucleon} \label{Eq3a} \]
L'énergie de liaison par nucléon d'un nucléide sur la courbe illustrée à la Figure\(\PageIndex{2}\)
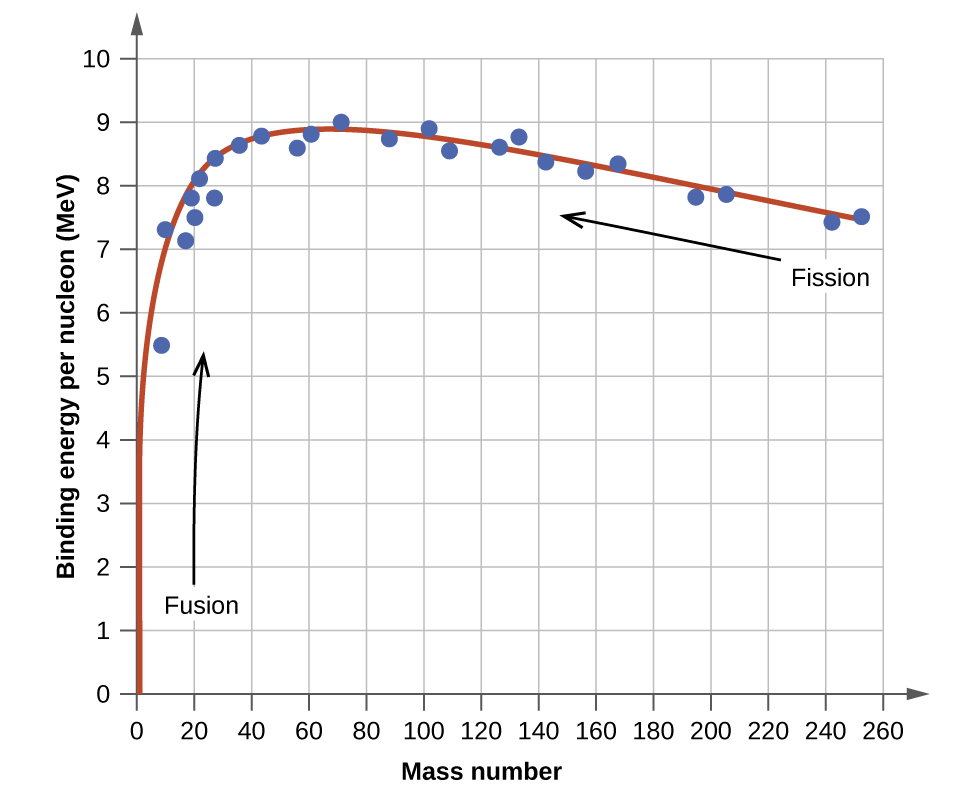
Le nucléide de fer\(\ce{^{56}_{26}Fe}\) se situe près du sommet de la courbe d'énergie de liaison (Figure\(\PageIndex{2}\)) et est l'un des nucléides les plus stables. Quelle est l'énergie de liaison par nucléon (en MeV) pour le nucléide\(\ce{^{56}_{26}Fe}\) (masse atomique de 55,9349 amu) ?
Solution
Comme dans l'exemple, nous déterminons d'abord le défaut de masse du nucléide, qui est la différence entre la masse de 26 protons, 30 neutrons et 26 électrons et la masse observée d'un\(\ce{^{56}_{26}Fe}\) atome :
\ [\ begin {align*}
\ mathrm {Masse \ : défaut} &= \ mathrm {[(26 × 1 0073 \ : amu) + (30 × 1 0087 \ : amu) + (26 × 0,00055 \ : amu)] −55,9349 \ : amu} \ \
&= \ mathrm {56.4651 \ : amu−55,9349 \ : amu} \ \
&= \ mathrm {0.5302 \ : amu}
\ end {align*} \ nonnumber \]
Nous calculons ensuite l'énergie de liaison d'un noyau à partir du défaut de masse en utilisant l'équation d'équivalence masse-énergie :
\ [\ begin {align*}
E&=MC^2= \ mathrm {0,5302 \ : amu× \ dfrac {1,6605 × 10^ {-27} \ :kg} {1 \ : amu} × (2,998 × 10^8 \ :m/s) ^2} \ \
&= \ mathrm {7,913 × 10^ {-1} \ : \ textrm kg⋅m} /s^2} \ \
&= \ mathrm {7,913 × 10^ {−11} \ :J}
\ end {align*} \ nonnumber \]
Nous convertissons ensuite l'énergie de liaison en joules par noyau en unités de MeV par nucléide :
\[\mathrm{7.913×10^{−11}\:J×\dfrac{1\: MeV}{1.602×10^{−13}\:J}=493.9\: MeV} \nonumber \]
Enfin, nous déterminons l'énergie de liaison par nucléon en divisant l'énergie de liaison nucléaire totale par le nombre de nucléons dans l'atome :
\[\textrm{Binding energy per nucleon}=\mathrm{\dfrac{493.9\: MeV}{56}=8.820\: MeV/nucleon} \nonumber \]
Notez que c'est presque 25 % plus élevé que l'énergie de liaison par nucléon pour\(\ce{^4_2He}\). (Notez également qu'il s'agit du même processus que dans l'exemple \ (\ PageIndex {2} \, mais avec l'étape supplémentaire de diviser l'énergie de liaison nucléaire totale par le nombre de nucléons.)
Quelle est l'énergie de liaison par nucléon dans\(\ce{^{19}_9F}\) (masse atomique, 18,9984 amu) ?
- Réponse
-
7,810 MeV/nucléon
Résumé
Un noyau atomique est constitué de protons et de neutrons, collectivement appelés nucléons. Bien que les protons se repoussent les uns les autres, le noyau est maintenu étroitement entre eux par une force à courte portée, mais très puissante, appelée force nucléaire forte. La masse d'un noyau est inférieure à la masse totale de ses nucléons constitutifs. Cette masse « manquante » est le défaut de masse, qui a été converti en énergie de liaison qui maintient le noyau ensemble selon l'équation d'équivalence masse-énergie d'Einstein, E = mc 2. Parmi les nombreux nucléides existants, seul un petit nombre est stable. Les nucléides contenant un nombre pair de protons ou de neutrons, ou ceux dont le nombre de nucléons est magique, sont particulièrement susceptibles d'être stables. Ces nucléides stables occupent une bande étroite de stabilité sur un graphique du nombre de protons par rapport au nombre de neutrons. L'énergie de liaison par nucléon est la plus élevée pour les éléments dont la masse est proche de 56 ; ce sont les noyaux les plus stables.
Équations clés
- E = cm 2
Lexique
- bande de stabilité
- (également ceinture de stabilité, zone de stabilité ou vallée de stabilité) région du graphique du nombre de protons par rapport au nombre de neutrons contenant des nucléides stables (non radioactifs)
- énergie de liaison par nucléon
- énergie de liaison totale pour le noyau divisée par le nombre de nucléons dans le noyau
- électronvolt (eV)
- unité de mesure des énergies de liaison nucléaire, 1 eV étant égal à la quantité d'énergie due au déplacement d'un électron sur une différence de potentiel électrique de 1 volt
- nombre magique
- noyaux contenant un nombre spécifique de nucléons se situant dans la bande de stabilité
- défaut de masse
- différence entre la masse d'un atome et la masse totale des particules subatomiques qui le constituent (ou la masse « perdue » lorsque les nucléons sont réunis pour former un noyau)
- équation d'équivalence masse-énergie
- La relation d'Albert Einstein montrant que masse et énergie sont équivalentes
- énergie de liaison nucléaire
- l'énergie perdue lorsque les nucléons d'un atome sont liés entre eux (ou l'énergie nécessaire pour décomposer un noyau en protons et neutrons qui le constituent)
- chimie nucléaire
- étude de la structure des noyaux atomiques et des processus qui modifient la structure nucléaire
- nucléon
- terme collectif désignant les protons et les neutrons d'un noyau
- nucléide
- noyau d'un isotope particulier
- radioactivité
- phénomène présenté par un nucléon instable qui se transforme spontanément en un nucléon plus stable ; un nucléon instable est dit radioactif
- radio-isotope
- isotope instable qui est en cours de conversion en un autre isotope plus stable
- force nucléaire puissante
- force d'attraction entre les nucléons qui maintient un noyau ensemble


