13.4 : Calculs d'équilibre

Last updated
Save as PDF

Page ID: 194034

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Écrire des équations représentant les changements de concentration et de pression pour les espèces chimiques dans les systèmes d'équilibre
Utiliser l'algèbre pour effectuer différents types de calculs d'équilibre

Nous savons qu'à l'équilibre, la valeur du quotient de réaction de toute réaction est égale à sa constante d'équilibre. Ainsi, nous pouvons utiliser l'expression mathématique de Q pour déterminer un certain nombre de quantités associées à une réaction à l'équilibre ou proche de l'équilibre. Bien que nous ayons appris à identifier la direction dans laquelle une réaction se déplacera pour atteindre l'équilibre, nous voulons étendre cette compréhension aux calculs quantitatifs. Pour ce faire, nous évaluons la façon dont les concentrations de produits et de réactifs changent lorsqu'une réaction approche de l'équilibre, en tenant compte des rapports stœchiométriques de la réaction. Cette approche algébrique des calculs d'équilibre sera explorée dans cette section.

Les variations des concentrations ou des pressions des réactifs et des produits se produisent lorsqu'un système réactionnel approche de l'équilibre. Dans cette section, nous verrons que nous pouvons relier ces changements les uns aux autres à l'aide des coefficients de l'équation chimique équilibrée décrivant le système. Nous prenons l'exemple de la décomposition de l'ammoniac.

Lors du chauffage, l'ammoniac se décompose de manière réversible en azote et en hydrogène selon cette équation :

\[\ce{2NH3}(g)⇌\ce{N2}(g)+\ce{3H2}(g) \nonumber \]

Si un échantillon d'ammoniac se décompose dans un système fermé et que la concentration de N ₂ augmente de 0,11 M, la variation de la concentration de N ₂, Δ [N ₂], la concentration finale moins la concentration initiale, est de 0,11 M. Le changement est positif car la concentration de N ₂ augmente.

La variation de la concentration de H ₂, Δ [H ₂], est également positive : la concentration de H ₂ augmente à mesure que l'ammoniac se décompose. L'équation chimique nous indique que la variation de la concentration de H ₂ est trois fois supérieure à la variation de la concentration de N ₂ car pour chaque mole de N ₂ produite, 3 moles de H ₂ sont produites.

\[ \begin{align*} \ce{Δ[H2]} &=3×\ce{Δ[N2]} \\[4pt] &=3×(0.11\:M) \\[4pt] &=0.33\:M \end{align*} \nonumber \]

La variation de la concentration de NH ₃, Δ [NH ₃], est le double de celle de Δ [N ₂] ; l'équation indique que 2 moles de NH ₃ doivent se décomposer pour chaque mole de N ₂ formée. Cependant, la variation de la concentration de NH ₃ est négative car la concentration d'ammoniac diminue au fur et à mesure de sa décomposition.

\[ \begin{align*} Δ[\ce{NH3}] &=−2×Δ[\ce{N2}] \\[4pt] &=−2×(0.11\:M) \\[4pt] &=−0.22\:M \end{align*} \nonumber \]

Nous pouvons relier ces relations directement aux coefficients de l'équation

\ [\ begin {align}
& \ fantôme {Δ [NH3} \ ce {2NH3} (g)

&&& \ fantôme {Δ [N2} \ ce {N2} (g)
&&+
&& \ fantôme {Δ [H2]} \ ce {3H2} (g) \ \
&Δ [\ ce {NH3}] =−2×Δ [\ ce {H3}] =−2×Δ [\ ce {N2] 2}] && Δ [\ ce {N2}] =0,1 \ :M & amp ; && Δ [\ ce {H2}] =3×Δ [\ ce {N2}]
\ end {align} \ nonnumber \]

Notez que toutes les modifications d'un côté des flèches sont du même signe et que toutes les modifications de l'autre côté des flèches sont du signe opposé.

Si nous ne connaissions pas l'ampleur de la variation de la concentration de N ₂, nous pourrions la représenter par le symbole x.

\(Δ[\ce{N2}]=x\)

Les variations des autres concentrations seraient alors représentées comme suit :

\(Δ[\ce{H2}]=3×Δ[\ce{N2}]=3x\)

\(Δ[\ce{NH3}]=−2×Δ[\ce{N2}]=−2x\)

Les coefficients des termes Δ sont identiques à ceux de l'équation équilibrée de la réaction.

\ (\ begin {alignat} {3}
& \ ce {2NH3} (g) \ :&& \ ce {N2} (g) + \ :&& \ ce {3H2} (g) \ \
&−2x &&x &&3x
\ end {alignat} \)

Le moyen le plus simple pour nous de déterminer les coefficients des variations de concentration dans une réaction quelconque est d'utiliser les coefficients de l'équation chimique équilibrée. Le signe du coefficient est positif lorsque la concentration augmente ; il est négatif lorsque la concentration diminue.

Exemple\(\PageIndex{1}\): Determining Relative Changes in Concentration

Compléter les modifications des concentrations pour chacune des réactions suivantes.

(a) \ (\ begin {alignat} {3}
& \ ce {C2H2} (g) + \ :&& \ ce {2Br2} (g) \ :&& \ ce {C2H2Br4} (g) \ \
&x && \ underline {\ hspace {40px}} && \ underline {\ hspace {40px}}
\ end {alignat} \)

(b) \ (\ begin {alignat} {3}
& \ ce {I2} (aq) + \ :&& \ ce {I-} (aq) \ :&& \ ce {I3-} (aq) \ \
& \ souligner {\ hspace {40px}} && \ underline {\ hspace {40px}} &&x
\ end {alignat} \)

(c) \ (\ begin {alignat} {3}
& \ ce {C3H8} (g) + \ :&& \ ce {5O2} (g) \ :&& \ ce {3CO2} (g) + \ :&& \ ce {4H2O} (g) \ \
&x && \ underline {\ hspace {40px}} && \ souligné {\ hspace {40px}} && \ underline {\ hspace {40px}}
\ end {alignat} \)

Une solution

(a) \ (\ begin {alignat} {3}
& \ ce {C2H2} (g) + \ :&& \ ce {2Br2} (g) \ :&& \ ce {C2H2Br4} (g) \ \
&x &&2x &&-x
\ end {alignat} \)

(b) \ (\ begin {alignat} {3}
& \ ce {I2} (aq) + \ :&& \ ce {I-} (aq) \ :&& \ ce {I3-} (aq) \ \
&-x &&-x &&x &x
\ end {alignat} \)

(c) \ (\ begin {alignat} {3}
& \ ce {C3H8} (g) + \ :&& \ ce {5O2} (g) \ :&& \ ce {3CO2} (g) + \ :&& \ ce {4H2O} (g) \ \
&x &&5x &&-3x &&-4x
\ end {alignat} \)

Exercice\(\PageIndex{1}\)

Compléter les modifications des concentrations pour chacune des réactions suivantes :

(a) \ (\ begin {alignat} {3}
& \ ce {2SO2} (g) + \ :&& \ ce {O2} (g) \ :&& \ ce {2SO3} (g) \ \
& \ souligner {\ hspace {40px}} &x && \ underline {\ hspace {40px}}
\ end {alignat} \)

(b) \ (\ begin {alignat} {3}
& \ ce {C4H8} (g) \ :&& \ ce {2C2H4} (g) \ \
& \ souligner {\ hspace {40px}} &&-2x
\ end {alignat} \)

(c) \ (\ begin {alignat} {3}
& \ ce {4NH3} (g) + \ :&& \ ce {7H2O} (g) \ :&& \ ce {4NO2} (g) + \ :&& \ ce {6H2O} (g) \ \
& \ underline {\ hspace {40px}} && \ souligné {\ hspace {40px}} souligner {\ hspace {40px}} && \ underline {\ hspace {40px}}
\ end { aligner} \)

Répondez à une: 2 x, x, −2 x
Réponse b: x, −2 x
Réponse c: 4 x, 7 x, −4 x, −6 x ou −4 x, −7 x, 4 x, 6 x

Calculs impliquant des concentrations d'équilibre

Comme la valeur du quotient de réaction de toute réaction à l'équilibre est égale à sa constante d'équilibre, nous pouvons utiliser l'expression mathématique de Q _c (c'est-à-dire la loi de l'action de masse) pour déterminer un certain nombre de quantités associées à une réaction à l'équilibre. Il peut être utile de garder à l'esprit que Q _c = K _c (à l'équilibre) dans toutes ces situations et qu'il n'existe que trois types de calculs de base :

Calcul d'une constante d'équilibre. Si les concentrations de réactifs et de produits à l'équilibre sont connues, la valeur de la constante d'équilibre de la réaction peut être calculée.
Calcul des concentrations d'équilibre manquantes. Si la valeur de la constante d'équilibre et toutes les concentrations d'équilibre, sauf une, sont connues, la concentration restante peut être calculée.
Calcul des concentrations d'équilibre à partir des concentrations initiales. Si la valeur de la constante d'équilibre et un ensemble de concentrations de réactifs et de produits qui ne sont pas à l'équilibre sont connues, les concentrations à l'équilibre peuvent être calculées.

Une liste similaire peut être générée en utilisant Q _P, K _P et une pression partielle. Nous chercherons à résoudre chacun de ces cas dans l'ordre.

Calcul d'une constante d'équilibre

Puisque la loi de l'action de masse est la seule équation dont nous disposons pour décrire la relation entre K _c et les concentrations de réactifs et de produits, tout problème que nous devons résoudre pour K _c doit fournir suffisamment d'informations pour déterminer le réactif et concentrations du produit à l'équilibre. Armés des concentrations, nous pouvons résoudre l'équation de K _c, car ce sera la seule inconnue.

L'exemple nous\(\PageIndex{1}\) a montré comment déterminer la constante d'équilibre d'une réaction si nous connaissons les concentrations de réactifs et de produits à l'équilibre. L'exemple suivant montre comment utiliser la stœchiométrie de la réaction et une combinaison de concentrations initiales et de concentrations d'équilibre pour déterminer une constante d'équilibre. Cette technique, communément appelée table ICE, pour l'équilibre initial, le changement de C et l'équilibre E, sera utile pour résoudre de nombreux problèmes d'équilibre. Un graphique est généré en commençant par la réaction d'équilibre en question. Sous la réaction, les concentrations initiales des réactifs et des produits sont répertoriées. Ces conditions sont généralement fournies par le problème et nous considérons qu'aucun changement vers l'équilibre ne s'est produit. La ligne de données suivante représente le changement qui se produit lorsque le système évolue vers l'équilibre. N'oubliez pas de prendre en compte la stœchiométrie des réactions décrite dans la section précédente de ce chapitre. La dernière ligne contient les concentrations une fois l'équilibre atteint.

Exemple\(\PageIndex{2}\): Calculation of an Equilibrium Constant

Les molécules d'iode réagissent de manière réversible avec les ions iodure pour produire des ions triiodure.

\[\ce{I2}(aq)+\ce{I-}(aq)⇌\ce{I3-}(aq) \nonumber \]

Si une solution dont les concentrations de I ₂ et de I ⁻ sont toutes deux égales à 1 000 × 10 ^-3 M avant la réaction donne une concentration d'équilibre de I ₂ de 6,61 × 10 ^-4 M, quelle est la constante d'équilibre de la réaction ?

Solution

Nous allons commencer ce problème en calculant les variations de concentration à mesure que le système atteint l'équilibre. Ensuite, nous déterminons les concentrations d'équilibre et, enfin, la constante d'équilibre. Tout d'abord, nous avons établi un tableau avec les concentrations initiales, les changements de concentrations et les concentrations d'équilibre en utilisant − x comme variation de la concentration de I ₂.

alt

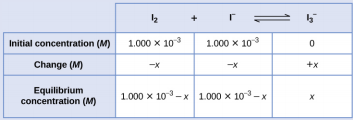
Puisque la concentration d'équilibre de I ₂ est donnée, on peut résoudre pour x. À l'équilibre, la concentration de I ₂ est de 6,61 × 10 ^-4 M, de sorte que

\(1.000×10^{−3}−x=6.61×10^{−4}\)

\(x=1.000×10^{−3}−6.61×10^{−4}\)

\(=3.39×10^{−4}\:M\)

Nous pouvons maintenant remplir le tableau avec les concentrations à l'équilibre.

alt

Nous calculons maintenant la valeur de la constante d'équilibre.

\(K_c=Q_c=\ce{\dfrac{[I3- ]}{[I2][I- ]}}\)

\(=\dfrac{3.39×10^{−4}\:M}{(6.61×10^{−4}\:M)(6.61×10^{−4}\:M)}=776\)

Exercice\(\PageIndex{2}\)

L'éthanol et l'acide acétique réagissent et forment de l'eau et de l'acétate d'éthyle, le solvant responsable de l'odeur de certains dissolvants pour vernis à ongles.

\(\ce{C2H5OH + CH3CO2H ⇌ CH3CO2C2H5 + H2O}\)

Lorsque l'on laisse réagir 1 mol de C ₂ H ₅ OH et de CH ₃ CO ₂ H dans 1 L du solvant dioxane, l'équilibre est établi lorsqu'il reste des\(\dfrac{1}{3}\) moles de chacun des réactifs. Calculez la constante d'équilibre de la réaction. (Remarque : L'eau n'est pas un solvant dans cette réaction.)

Réponse: K _c = 4

Calcul d'une concentration d'équilibre manquante

Si nous connaissons la constante d'équilibre d'une réaction et les concentrations à l'équilibre de tous les réactifs et produits sauf un, nous pouvons calculer la concentration manquante.

Exemple\(\PageIndex{3}\): Calculation of a Missing Equilibrium Concentration

Les oxydes d'azote sont des polluants atmosphériques produits par la réaction de l'azote et de l'oxygène à des températures élevées. À 2000 °C, la valeur de la constante d'équilibre de la réaction est de 4,1 × 10 ⁻⁴.\(\ce{N2}(g)+\ce{O2}(g)⇌\ce{2NO}(g)\) Déterminez la concentration de NO (g) dans un mélange d'équilibre avec de l'air à une pression de 1 atm à cette température. Dans l'air, [N ₂] = 0,036 mol/L et [O ₂] 0,0089 mol/L.

Solution

On nous donne toutes les concentrations d'équilibre à l'exception de celle de NO. Ainsi, nous pouvons résoudre la concentration d'équilibre manquante en réorganisant l'équation de la constante d'équilibre.

\(K_c=Q_c=\ce{\dfrac{[NO]^2}{[N2][O2]}}\)

\(\ce{[NO]^2}=K_c\ce{[N2][O2]}\)

\(\ce{[NO]}=\sqrt{K_c\ce{[N2][O2]}}\)

\(=\sqrt{(4.1×10^{−4})(0.036)(0.0089)}\)

\(=\sqrt{1.31×10^{−7}}\)

\(=3.6×10^{−4}\)

Ainsi, [NO] est de 3,6 × 10 ⁻⁴ mol/L à l'équilibre dans ces conditions.

Nous pouvons vérifier notre réponse en substituant toutes les concentrations d'équilibre dans l'expression du quotient de réaction pour voir s'il est égal à la constante d'équilibre.

\[ \begin{align*} Q_c=\ce{\dfrac{[NO]^2}{[N2][O2]}} \\[4pt] &=\dfrac{(3.6×10^{−4})^2}{(0.036)(0.0089)} \\[4pt] &=4.0×10^{−4}=K_c \end{align*} \nonumber \]

La réponse est vérifiée ; notre valeur calculée donne la constante d'équilibre dans les limites de l'erreur associée aux chiffres significatifs du problème.

Exercice\(\PageIndex{3}\)

La constante d'équilibre pour la réaction de l'azote et de l'hydrogène pour produire de l'ammoniac à une certaine température est de 6,00 × 10 ⁻². Calculer la concentration d'équilibre d'ammoniac si les concentrations d'équilibre d'azote et d'hydrogène sont de 4,26 M et 2,09 M, respectivement.

Réponse: 1,53 mol/L

Calcul des variations de concentration

Si nous connaissons la constante d'équilibre d'une réaction et un ensemble de concentrations de réactifs et de produits qui ne sont pas à l'équilibre, nous pouvons calculer les variations des concentrations lorsque le système atteint l'équilibre, ainsi que les nouvelles concentrations à l'équilibre. La procédure type peut être résumée en quatre étapes.

Déterminez la direction dans laquelle la réaction se déroule pour atteindre l'équilibre.
- Écrivez une équation chimique équilibrée pour la réaction.
- Si la direction dans laquelle la réaction doit se dérouler pour atteindre l'équilibre n'est pas évidente, calculez Q _c à partir des concentrations initiales et comparez-le à K _c pour déterminer la direction du changement.
Déterminez les changements relatifs nécessaires pour atteindre l'équilibre, puis écrivez les concentrations d'équilibre en fonction de ces changements.
- Définissez les changements des concentrations initiales nécessaires pour que la réaction atteigne l'équilibre. En général, nous représentons la plus petite modification par le symbole x et exprimons les autres modifications en termes de plus petite modification.
- Définissez les concentrations d'équilibre manquantes en fonction des concentrations initiales et des variations de concentration déterminées en (a).
Résolvez le changement et les concentrations d'équilibre.
- Substituez les concentrations d'équilibre dans l'expression de la constante d'équilibre, résolvez x et vérifiez toutes les hypothèses utilisées pour trouver x.
- Calculez les concentrations d'équilibre.
Vérifiez l'arithmétique.
- Vérifiez les concentrations d'équilibre calculées en les substituant dans l'expression d'équilibre et en déterminant si elles donnent la constante d'équilibre.

Parfois, une étape particulière peut différer d'un problème à l'autre ; elle peut être plus complexe pour certains problèmes et moins complexe pour d'autres. Cependant, chaque calcul de concentrations d'équilibre à partir d'un ensemble de concentrations initiales impliquera ces étapes.

Pour résoudre des problèmes d'équilibre impliquant des changements de concentration, il est parfois pratique de mettre en place une table ICE, comme décrit dans la section précédente.

Exemple\(\PageIndex{4}\): Calculation of Concentration as a Reaction Equilibrates

Dans certaines conditions, la constante d'équilibre pour la décomposition du PCl ₅ (g) en PCl ₃ (g) et en Cl ₂ (g) est de 0,0211. Quelles sont les concentrations d'équilibre de PCl ₅, de PCl ₃ et de Cl ₂ si la concentration initiale de PCl ₅ était de 1,00 M ?

Solution

Utilisez le processus par étapes décrit précédemment.

L'équation équilibrée pour la décomposition du PCl ₅ est
\(\ce{PCl5}(g)⇌\ce{PCl3}(g)+\ce{Cl2}(g)\)

Comme nous n'avons pas de produits au départ, Q _c = 0 et la réaction se poursuivra vers la droite.

Rereprésentons l'augmentation de la concentration de PCl ₃ par le symbole x. Les autres changements peuvent être écrits en termes de x en tenant compte des coefficients de l'équation chimique.
\ (\ begin {alignat} {3}
& \ ce {PCl5} (g) \ :&& \ ce {PCl3} (g) + \ :&& \ ce {Cl2} (g) \ \
&-x &x &x &x &x
\ end {alignat} \)
Les changements de concentration et les expressions des concentrations d'équilibre sont les suivants :

Ce tableau comporte deux colonnes principales et quatre rangées. La première ligne de la première colonne ne comporte pas de titre et contient les informations suivantes dans la première colonne : Concentration initiale (M), Variation (M), Concentration d'équilibre (M). La deuxième colonne contient l'en-tête « P C l indice 5 flèche d'équilibre P C l indice 3 plus C l indice 2 ». Sous la deuxième colonne se trouve un sous-groupe de trois lignes et trois colonnes. La première colonne contient les éléments suivants : 1,00, x négatif, 1,00 moins x. La deuxième colonne contient les éléments suivants : 0, x positif, 0 plus x est égal à x. La troisième colonne contient les éléments suivants : 0, x positif, 0 plus x est égal à x.
La substitution des concentrations d'équilibre dans l'équation de la constante d'équilibre donne
\(K_c=\ce{\dfrac{[PCl3][Cl2]}{[PCl5]}}=0.0211\)

\(=\dfrac{(x)(x)}{(1.00−x)}\)

Cette équation ne contient qu'une seule variable, x, le changement de concentration. Nous pouvons écrire l'équation sous forme d'équation quadratique et résoudre x à l'aide de la formule quadratique.

\(0.0211=\dfrac{(x)(x)}{(1.00−x)}\)

\(0.0211(1.00−x)=x^2\)

\(x^2+0.0211x−0.0211=0\)

Une équation de la forme ax ² + bx + c = 0 peut être réarrangée pour résoudre x :

\(x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}\)

Dans ce cas, a = 1, b = 0,0211 et c = −0,0211. En substituant les valeurs appropriées à a, b et c, on obtient :

\(x=\dfrac{−0.0211±\sqrt{(0.0211)^2−4(1)(−0.0211)}}{2(1)}\)

\(=\dfrac{−0.0211±\sqrt{(4.45×10^{−4})+(8.44×10^{−2})}}{2}\)

\(=\dfrac{−0.0211±0.291}{2}\)

D'où

\(x=\dfrac{−0.0211+0.291}{2}=0.135\)

ou

\(x=\dfrac{−0.0211−0.291}{2}=−0.156\)

Les équations quadratiques ont souvent deux solutions différentes, l'une physiquement possible et l'autre physiquement impossible (racine étrangère). Dans ce cas, la deuxième solution (−0,156) est physiquement impossible car nous savons que le changement doit être un nombre positif (sinon nous obtiendrions des valeurs négatives pour les concentrations des produits). Ainsi, x = 0,135 M.

Les concentrations d'équilibre sont

\(\ce{[PCl5]}=1.00−0.135=0.87\:M\)
\(\ce{[PCl3]}=x=0.135\:M\)
\(\ce{[Cl2]}=x=0.135\:M\)
La substitution dans l'expression de K _c (pour vérifier le calcul) donne
\(K_c=\ce{\dfrac{[PCl3][Cl2]}{[PCl5]}}=\dfrac{(0.135)(0.135)}{0.87}=0.021\)

La constante d'équilibre calculée à partir des concentrations d'équilibre est égale à la valeur de K _c indiquée dans le problème (arrondie au nombre approprié de chiffres significatifs). Ainsi, les concentrations d'équilibre calculées sont vérifiées.

Exercice\(\PageIndex{4A}\)

L'acide acétique, CH ₃ CO ₂ H, réagit avec l'éthanol, C ₂ H ₅ OH, pour former de l'eau et de l'acétate d'éthyle, CH ₃ CO ₂ C ₂ H ₅.

\[\ce{CH3CO2H + C2H5OH ⇌ CH3CO2C2H5 + H2O} \nonumber \]

La constante d'équilibre pour cette réaction avec le dioxane comme solvant est de 4,0. Quelles sont les concentrations d'équilibre lorsqu'un mélange est égal à 0,15 M dans CH ₃ CO ₂ H, 0,15 M dans C ₂ H ₅ OH, 0,40 M dans CH ₃ CO ₂ _{C 2} H ₅ et 0,40 M dans H ₂ O sont-ils mélangés à suffisamment de dioxane pour obtenir 1,0 L de solution ?

Réponse: [CH ₃ CO ₂ H] = 0,36 M, [C ₂ H ₅ OH] = 0,36 M, [CH ₃ CO ₂ C ₂ H ₅] = 0,17 M, [H ₂ O] = 0,17 M

Exercice\(\PageIndex{4B}\)

Un flacon de 1 L est rempli de 1,00 moles de H ₂ et de 2,00 moles de I ₂. La valeur de la constante d'équilibre pour la réaction de l'hydrogène et de l'iode réagissant pour former de l'iodure d'hydrogène est de 50,5 dans les conditions données. Quelles sont les concentrations d'équilibre de H ₂, I ₂ et HI en moles/L ?

\[\ce{H2}(g)+\ce{I2}(g)\rightleftharpoons\ce{2HI}(g) \nonumber \]

Réponse: [H ₂] = 0,06 M, [I ₂] = 1,06 M, [HI] = 1,88 M

Il est parfois possible d'utiliser les connaissances chimiques pour trouver des solutions à des problèmes d'équilibre sans réellement résoudre une équation quadratique (ou plus complexe). Tout d'abord, il est utile de vérifier que l'équilibre peut être obtenu à partir de deux extrêmes : tous (ou presque) les réactifs et tous (ou presque) les produits.

Prenons l'exemple de l'ionisation de 0,150 M HA, un acide faible.

\(\ce{HA}(aq)⇌\ce{H+}(aq)+\ce{A-}(aq) \hspace{20px} K_c=6.80×10^{−4}\)

Le moyen le plus évident de déterminer les concentrations d'équilibre serait de commencer avec les seuls réactifs. Cela pourrait être appelé le point de départ « tous les réactifs ». En utilisant x pour la quantité d'acide ionisé à l'équilibre, on obtient la table ICE et la solution.

Ce tableau comporte deux colonnes principales et quatre rangées. La première ligne de la première colonne ne comporte pas de titre et contient ensuite les éléments suivants : pression initiale (M), variation (M), équilibre (M). La deuxième colonne contient l'en-tête « H A (a q) flèche d'équilibre H exposant plus signe (a q) plus A indice signe négatif (a q) ». Sous la deuxième colonne se trouve un sous-groupe de trois colonnes et trois rangées. La première colonne contient les éléments suivants : 0,150, x négatif, 0,150 moins x. La deuxième colonne contient les éléments suivants : 0, x, x. La troisième colonne contient les éléments suivants : 0, x, x.

La mise en place et la résolution de l'équation quadratique donnent

\(K_c=\ce{\dfrac{[H+][A- ]}{[HA]}}=\dfrac{(x)(x)}{(0.150−x)}=6.80×10^{−4}\)

\(x^2+6.80×10^{−4}x−1.02×10^{−4}=0\)

\(x={−6.80×10^{−4}±\sqrt{(6.80×10^{−4})^2−(4)(1)(−1.02×10^{−4})}}{(2)(1)}\)

\(x=0.00977\:M\textrm{ or }−0.0104\:M\)

En utilisant la racine positive (physique), les concentrations d'équilibre sont

\(\ce{[HA]}=0.150−x=0.140\:M\)

\(\ce{[H+]}=\ce{[A- ]}=x=0.00977\:M\)

Une façon moins évidente de résoudre le problème serait de supposer que tout l'AH s'ionise d'abord, puis que le système s'équilibre. Cela pourrait être appelé le point de départ « tous les produits ». En supposant que tout le HA s'ionise donne

\(\ce{[HA]}=0.150−0.150=0\:M\)

\(\ce{[H+]}=0+0.150=0.150\:M\)

\(\ce{[A- ]}=0+0.150=0.150\:M\)

En les utilisant comme concentrations initiales et « y » pour représenter la concentration de HA à l'équilibre, voici le tableau ICE pour ce point de départ.

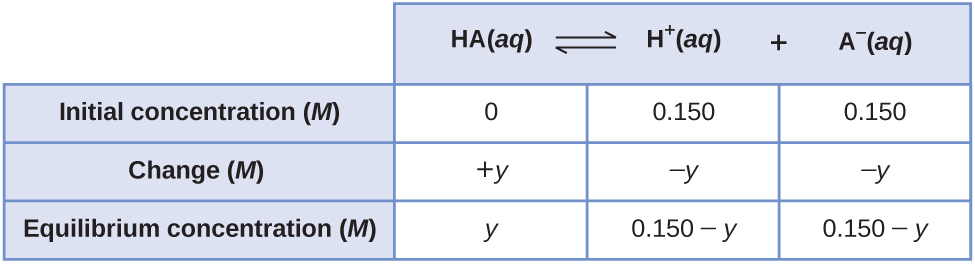
La mise en place et la résolution de l'équation quadratique donnent

\(K_c=\ce{\dfrac{[H+][A- ]}{[HA]}}=\dfrac{(0.150−y)(0.150−y)}{(y)}=6.80×10^{−4}\)

\(6.80×10^{−4}y=0.0225−0.300y+y^2\)

Conservez quelques chiffres significatifs supplémentaires afin de minimiser les problèmes d'arrondissement.

\(y^2−0.30068y+0.022500=0\)

\(y=\dfrac{0.30068±\sqrt{(0.30068)^2−(4)(1)(0.022500)}}{(2)(1)}\)

\(y=\dfrac{0.30068±0.020210}{2}\)

En arrondissant chaque solution à trois chiffres significatifs, on obtient

\(y=0.160\:M\textrm{ or }y=0.140\:M\)

En utilisant la racine physiquement significative (0,140 M), on obtient les concentrations d'équilibre comme

\(\ce{[HA]}=y=0.140\:M\)

\(\ce{[H+]}=0.150−y=0.010\:M\)

\(\ce{[A- ]}=0.150−y=0.010\:M\)

Ainsi, les deux approches donnent les mêmes résultats (à trois décimales) et montrent que les deux points de départ mènent aux mêmes conditions d'équilibre. Le point de départ « tous les réactifs » a entraîné un changement relativement faible (x) parce que le système était proche de l'équilibre, tandis que le point de départ « tous les produits » présentait un changement relativement important (y) proche de l'ampleur des concentrations initiales. On peut dire qu'un système qui démarre « près » de l'équilibre n'aura besoin que d'un « petit » changement des conditions (x) pour atteindre l'équilibre.

Rappelons qu'un faible K _c signifie que très peu de réactifs forment des produits et qu'un K _c élevé signifie que la plupart des réactifs forment des produits. Si le système peut être agencé de manière à démarrer « près » de l'équilibre, alors si le changement (x) est faible par rapport aux concentrations initiales, il peut être négligé. Une valeur faible est généralement définie comme entraînant une erreur inférieure à 5 %. Les deux exemples suivants le démontrent.

Exemple\(\PageIndex{5}\): Approximate Solution Starting Close to Equilibrium

Quelles sont les concentrations à l'équilibre d'une solution de 0,15 M de HCN ?

\[\ce{HCN}(aq)⇌\ce{H+}(aq)+\ce{CN-}(aq) \hspace{20px} K_c=4.9×10^{−10} \nonumber \]

Solution 1

L'utilisation de « x » pour représenter la concentration de chaque produit à l'équilibre donne ce tableau ICE.

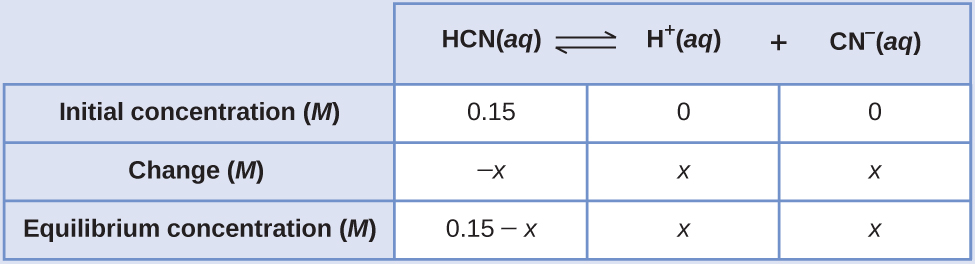
La solution exacte peut être obtenue en utilisant la formule quadratique avec

\[K_c=\dfrac{(x)(x)}{0.15−x} \nonumber \]

la résolution

\[x^2+4.9×10^{−10}−7.35×10^{−11}=0 \nonumber \]

\[x=8.56×10^{−6}\:M\textrm{ (3 sig. figs.)}=8.6×10^{−6}\:M\textrm{ (2 sig. figs.)} \nonumber \]

Ainsi, [H ⁺] = [CN ^—] = x = 8,6 × 10 ^—6 M et [HCN] = 0,15 — x = 0,15 M.

Dans ce cas, l'intuition chimique peut fournir une solution plus simple. À partir de la constante d'équilibre et des conditions initiales, x doit être petit par rapport à 0,15 M. Plus formellement, si\(x≪0.15\), alors 0,15 — x ≈ 0,15. Si cette hypothèse est vraie, cela simplifie l'obtention de x

\[K_c=\dfrac{(x)(x)}{0.15−x}≈\dfrac{x^2}{0.15} \nonumber \]

\[4.9×10^{−10}=\dfrac{x^2}{0.15} \nonumber \]

\[x^2=(0.15)(4.9×10^{−10})=7.4×10^{−11} \nonumber \]

\[x=\sqrt{7.4×10^{−11}}=8.6×10^{−6}\:M \nonumber \]

Dans cet exemple, la résolution de l'équation exacte (quadratique) et l'utilisation d'approximations ont donné le même résultat à deux chiffres significatifs. Bien que la plupart du temps, l'approximation soit légèrement différente de la solution exacte, tant que l'erreur est inférieure à 5 %, la solution approximative est considérée comme valide. Dans ce problème, le 5 % s'applique à IF (0,15 — x) ≈ 0,15 M, donc si

\[\dfrac{x}{0.15}×100\%=\dfrac{8.6×10^{−6}}{0.15}×100\%=0.006\% \nonumber \]

est inférieur à 5 %, comme c'est le cas dans ce cas, l'hypothèse est valide. La solution approximative est donc une solution valide.

Exercice\(\PageIndex{5}\)

Quelles sont les concentrations d'équilibre dans une solution de NH ₃ à 0,25 M ?

\(\ce{NH3}(aq)+\ce{H2O}(l)⇌\ce{NH4+}(aq)+\ce{OH-}(aq) \hspace{20px} K_c=1.8×10^{−5}\)

Supposons que x soit bien inférieur à 0,25 M et calculez l'erreur dans votre hypothèse.

Réponse: \(\ce{[OH- ]}=\ce{[NH4+]}=0.0021\:M\); [NH ₃] = 0,25 M, erreur = 0,84 %

Le second exemple nécessite que les informations d'origine soient traitées un peu, mais elles peuvent toujours être résolues à l'aide d'une petite approximation de x.

Exemple\(\PageIndex{6}\): Approximate Solution After Shifting Starting Concentration

Les ions cuivre (II) forment un ion complexe en présence d'ammoniac

\[\ce{Cu^2+}(aq)+\ce{4NH3}(aq)⇌\ce{Cu(NH3)4^2+}(aq) \hspace{20px} K_c=5.0×10^{13}=\ce{\dfrac{[Cu(NH3)4^2+]}{[Cu^2+(aq)][NH3]^4}} \nonumber \]

Si 0,010 mol de Cu ² ⁺ est ajouté à 1,00 L d'une solution contenant 1,00 M de NH ₃, quelles sont les concentrations lorsque le système arrive à l'équilibre ?

Solution La concentration initiale en cuivre (II) est de 0,010 M. La constante d'équilibre étant très grande, il serait préférable de commencer avec le plus de produit possible, car « tous les produits » sont beaucoup plus proches de l'équilibre que « tous les réactifs ». Notez que le Cu ² ⁺ est le réactif limite ; si la totalité de 0,010 M réagit pour former un produit, les concentrations seraient

\[\ce{[Cu^2+]}=0.010−0.010=0\:M \nonumber \]

\[\ce{[Cu(NH3)4^2+]}=0.010\:M \nonumber \]

\[\ce{[NH3]}=1.00−4×0.010=0.96\:M \nonumber \]

En utilisant ces valeurs « décalées » comme concentrations initiales avec x comme concentration en ions cuivre (II) libres à l'équilibre, on obtient ce tableau ICE.

Puisque nous commençons près de l'équilibre, x doit être petit de telle sorte que

\(0.96+4x≈0.96\:M\)

\(0.010−x≈0.010\:M\)

\(K_c=\dfrac{(0.010−x)}{x(0.96−4x)^4}≈\dfrac{(0.010)}{x(0.96)^4}=5.0×10^{13}\)

\(x=\dfrac{(0.010)}{K_c(0.96)^4}=2.4×10^{−16}\:M\)

Sélectionnez la plus petite concentration pour la règle des 5 %.

\(\dfrac{2.4×10^{−16}}{0.010}×100\%=2×10^{−12}\%\)

C'est beaucoup moins de 5 %, donc les hypothèses sont valides. Les concentrations à l'équilibre sont

\(\ce{[Cu^2+]}=x=2.4×10^{−16}\:M\)

\(\ce{[NH3]}=0.96−4x=0.96\:M\)

\(\ce{[Cu(NH3)4^2+]}=0.010−x=0.010\:M\)

En commençant par la quantité maximale de produit, ce système était proche de l'équilibre et la variation (x) était très faible. Avec seulement un petit changement nécessaire pour atteindre l'équilibre, l'équation de x a été grandement simplifiée et a donné un résultat valide bien en deçà de la marge d'erreur maximale de 5 %.

Exercice\(\PageIndex{6}\)

Quelles sont les concentrations d'équilibre lorsque 0,25 mol de Ni ² ⁺ est ajouté à 1,00 L de solution de NH ₃ à 2,00 M ?

\[\ce{Ni^2+}(aq)+\ce{6NH3}(aq)⇌\ce{Ni(NH3)6^2+}(aq) \nonumber \]

avec\(K_c=5.5×10^8\).

Avec une constante d'équilibre aussi élevée, formez d'abord autant de produit que possible, puis supposons que seule une petite quantité (x) du produit se déplace vers la gauche. Calculez l'erreur dans votre hypothèse.

Réponse: \(\ce{[Ni(NH3)6^2+]}=0.25\:M\), [NH ₃] = 0,50 M, [Ni ² ⁺] = 2,9 × 10 ^—8 M, erreur = 1,2 × 10 ^—5 %

Résumé

Les rapports du taux de variation des concentrations d'une réaction sont égaux aux rapports des coefficients de l'équation chimique équilibrée. Le signe du coefficient de X est positif lorsque la concentration augmente et négatif lorsqu'elle diminue. Nous avons appris à aborder trois types fondamentaux de problèmes d'équilibre. Lorsque l'on donne les concentrations des réactifs et des produits à l'équilibre, on peut résoudre la constante d'équilibre ; lorsqu'on lui donne la constante d'équilibre et certaines des concentrations impliquées, on peut résoudre les concentrations manquantes ; et lorsqu'on lui donne la constante d'équilibre et les concentrations initiales, nous pouvons résoudre les concentrations à l'équilibre.