13.2 : Constantes d'équilibre

Last updated
Save as PDF

Page ID: 194033

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Déterminer les quotients de réaction à partir d'équations chimiques représentant des réactions homogènes et hétérogènes
Calculer les valeurs des quotients de réaction et des constantes d'équilibre en utilisant les concentrations et les pressions
Établir un lien entre l'amplitude d'une constante d'équilibre et les propriétés du système chimique

Maintenant que nous avons un symbole (\(\rightleftharpoons\)) pour désigner les réactions réversibles, nous aurons besoin d'un moyen d'exprimer mathématiquement comment les quantités de réactifs et de produits affectent l'équilibre du système. Une équation générale pour une réaction réversible peut être écrite comme suit :

\[m\ce{A}+n\ce{B}+ \rightleftharpoons x\ce{C}+y\ce{D} \label{13.3.1} \]

Nous pouvons écrire le quotient de réaction (\(Q\)) pour cette équation. Lorsqu'il est évalué à l'aide de concentrations, il est appelé\(Q_c\). Nous utilisons des parenthèses pour indiquer les concentrations molaires des réactifs et des produits.

\[ Q_c=\dfrac{[\ce{C}]^x[\ce{D}]^y}{[\ce{A}]^m[\ce{B}]^n} \label{13.3.2} \]

Le quotient de réaction est égal aux concentrations molaires des produits de l'équation chimique (multipliées ensemble) sur les réactifs (également multipliées ensemble), chaque concentration étant portée à la puissance du coefficient de cette substance dans l'équation chimique équilibrée. Par exemple, le quotient de réaction pour la réaction réversible

\[\ce{2NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \label{13.3.3} \]

est donné par cette expression :

\[Q_c=\ce{\dfrac{[N_2O_4]}{[NO_2]^2}} \label{13.3.4} \]

Exemple\(\PageIndex{1}\): Writing Reaction Quotient Expressions

Écrivez l'expression du quotient de réaction pour chacune des réactions suivantes :

\(\ce{3O}_{2(g)} \rightleftharpoons \ce{2O}_{3(g)}\)
\(\ce{N}_{2(g)}+\ce{3H}_{2(g)} \rightleftharpoons \ce{2NH}_{3(g)}\)
\(\ce{4NH}_{3(g)}+\ce{7O}_{2(g)} \rightleftharpoons \ce{4NO}_{2(g)}+\ce{6H_2O}_{(g)}\)

Solution

\(Q_c=\dfrac{[\ce{O3}]^2}{[\ce{O2}]^3}\)
\( Q_c=\dfrac{[\ce{NH3}]^2}{\ce{[N2][H2]}^3}\)
\( Q_c=\dfrac{\ce{[NO2]^4[H2O]^6}}{\ce{[NH3]^4[O2]^7}}\)

Exercice\(\PageIndex{1}\)

Écrivez l'expression du quotient de réaction pour chacune des réactions suivantes :

\( \ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g)\)
\( \ce{C4H8}(g) \rightleftharpoons \ce{2C2H4}(g)\)
\( \ce{2C4H10}(g)+\ce{13O2}(g) \rightleftharpoons \ce{8CO2}(g)+\ce{10H2O}(g)\)

Répondez à: \( Q_c=\dfrac{[\ce{SO3}]^2}{\ce{[SO2]^2[O2]}}\)
Réponse b: \( Q_c=\dfrac{[\ce{C2H4}]^2}{[\ce{C4H8}]}\)
Réponse c: \( Q_c=\dfrac{\ce{[CO2]^8[H2O]^{10}}}{\ce{[C4H10]^2[O2]^{13}}}\)

La valeur numérique de\(Q_c\) pour une réaction donnée varie ; elle dépend des concentrations de produits et de réactifs présents au moment de\(Q_c\) la détermination. Lorsque des réactifs purs sont mélangés,\(Q_c\) vaut initialement zéro car aucun produit n'est présent à ce stade. Au fur et à mesure que la réaction se poursuit, la valeur de\(Q_c\) augmente à mesure que les concentrations des produits augmentent et que les concentrations des réactifs diminuent simultanément (Figure\(\PageIndex{1}\)). Lorsque la réaction atteint l'équilibre, la valeur du quotient de réaction ne change plus car les concentrations ne changent plus.

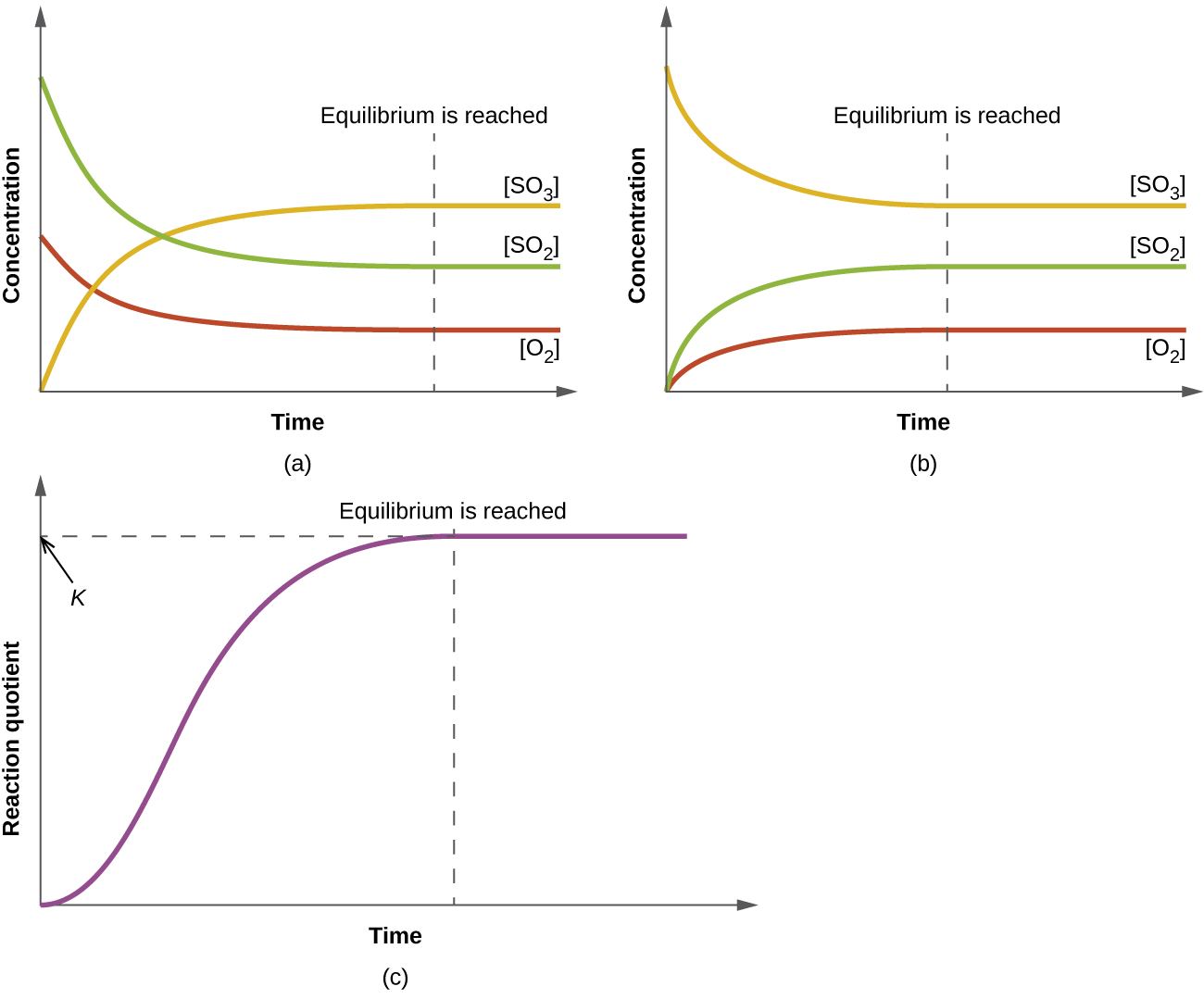
Figure\(\PageIndex{1}\) : (a) La variation des concentrations de réactifs et de produits est illustrée lorsque la\(\ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g)\) réaction approche de l'équilibre. (b) La variation des concentrations de réactifs et de produits est décrite lorsque la réaction\(\ce{2SO3}(g) \rightleftharpoons \ce{2SO2}(g)+\ce{O2}(g)\) approche de l'équilibre. (c) Le graphique montre l'évolution de la valeur du quotient de réaction lorsque la réaction approche de l'équilibre.

Lorsqu'un mélange de réactifs et de produits d'une réaction atteint l'équilibre à une température donnée, son quotient de réaction a toujours la même valeur. Cette valeur est appelée constante d'équilibre (\(K\)) de la réaction à cette température. Quant au quotient de réaction, lorsqu'il est évalué en termes de concentrations, il est noté comme\(K_c\).

Le fait qu'un quotient de réaction prenne toujours la même valeur à l'équilibre peut être exprimé comme suit :

\[Q_c \textrm{ at equilibrium}=K_c=\dfrac{[\ce C]^x[\ce D]^y...}{[\ce A]^m[\ce B]^n...} \label{13.3.5} \]

Cette équation est un énoncé mathématique de la loi de l'action de masse : lorsqu'une réaction atteint l'équilibre à une température donnée, le quotient de réaction pour la réaction a toujours la même valeur.

Exemple\(\PageIndex{2}\): Evaluating a Reaction Quotient

Le dioxyde d'azote gazeux forme du tétroxyde d'azote selon cette équation :

\[\ce{2NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \nonumber \]

Lorsque 0,10 mol\(\ce{NO2}\) est ajouté à une fiole de 1,0 L à 25 °C, la concentration change de telle sorte qu'à l'équilibre, [NO ₂] = 0,016 M et [N ₂ O ₄] = 0,042 M.

Quelle est la valeur du quotient de réaction avant qu'une réaction ne se produise ?
Quelle est la valeur de la constante d'équilibre de la réaction ?

Solution

Avant la formation de tout produit\(\mathrm{[NO_2]=\dfrac{0.10\:mol}{1.0\:L}}=0.10\:M\), et [N ₂ O ₄] = 0 M. Ainsi,\[Q_c=\ce{\dfrac{[N2O4]}{[NO2]^2}}=\dfrac{0}{0.10^2}=0 \nonumber \]
À l'équilibre, la valeur de la constante d'équilibre est égale à la valeur du quotient de réaction. À l'équilibre,\[K_c=Q_c=\ce{\dfrac{[N2O4]}{[NO2]^2}}=\dfrac{0.042}{0.016^2}=1.6\times 10^2. \nonumber \]

La constante d'équilibre est de 1,6 × 10 ².

Notez que l'analyse dimensionnelle suggère que l'unité de cette\(K_c\) valeur devrait être M ^-1. Cependant, il est courant d'omettre les unités pour\(K_c\) les valeurs calculées comme décrit ici, car c'est l'amplitude d'une constante d'équilibre qui transmet les informations utiles. Comme nous le verrons plus loin dans ce module, l'approche rigoureuse du calcul des constantes d'équilibre utilise des quantités adimensionnelles dérivées des activités plutôt que des concentrations molaires, de sorte que les\(K_c\) valeurs sont vraiment sans unités.

Exercice\(\PageIndex{2}\)

Pour la réaction

\[\ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g) \nonumber \]

les concentrations à l'équilibre sont [SO ₂] = 0,90 M, [O ₂] = 0,35 M et [SO ₃] = 1,1 M. Quelle est la valeur de la constante d'équilibre, K _c ?

Réponse: K _c = 4,3

L'amplitude d'une constante d'équilibre est une mesure du rendement d'une réaction lorsqu'elle atteint l'équilibre. Une valeur élevée pour\(K_c\) indique que l'équilibre n'est atteint que lorsque les réactifs ont été largement convertis en produits. Une faible valeur\(K_c\), bien inférieure à 1, indique que l'équilibre est atteint lorsque seule une faible proportion des réactifs a été convertie en produits.

Une fois que la valeur de\(K_c\) est connue pour une réaction, elle peut être utilisée pour prédire les changements de direction par rapport à la valeur de\(Q_c\). Un système qui n'est pas en équilibre évoluera dans la direction qui établit l'équilibre. Les données de la figure\(\PageIndex{2}\) illustrent cela. Lorsqu'ils sont chauffés à une température constante, 800 °C, différents mélanges de départ de\(\ce{CO}\)\(\ce{H_2O}\),\(\ce{CO_2}\), et\(\ce{H_2}\) réagissent pour atteindre des compositions respectant le même équilibre (la valeur de\(Q_c\) change jusqu'à ce qu'elle soit égale à la valeur de K _c). Cette valeur est de 0,640, la constante d'équilibre de la réaction dans ces conditions.

\[\ce{CO}(g)+\ce{H2O}(g) \rightleftharpoons \ce{CO2}(g)+\ce{H2}(g) \hspace{20px} K_c=0.640 \hspace{20px} \mathrm{T=800°C} \label{13.3.6} \]

Il est important de reconnaître qu'un équilibre peut être établi à partir de réactifs ou de produits, ou d'un mélange des deux. Par exemple, l'équilibre a été établi à partir du mélange 2 de la figure\(\PageIndex{2}\) lorsque les produits de la réaction ont été chauffés dans un récipient fermé. En fait, l'une des techniques utilisées pour déterminer si une réaction est réellement à l'équilibre consiste à aborder l'équilibre en commençant par les réactifs dans une expérience et en commençant par les produits dans une autre. Si la même valeur du quotient de réaction est observée lorsque les concentrations cessent de changer dans les deux expériences, nous pouvons être certains que le système a atteint l'équilibre.

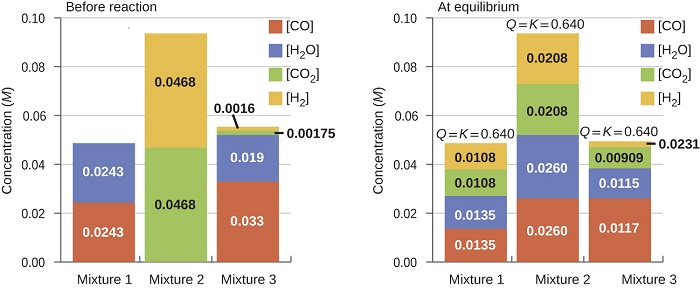
Figure\(\PageIndex{2}\) : Les concentrations de trois mélanges sont indiquées avant et après avoir atteint l'équilibre à 800 °C pour la réaction dite de déplacement des gaz de l'eau (équation \ ref {13.3.6}).

Exemple\(\PageIndex{3}\): Predicting the Direction of Reaction

Voici les concentrations de départ des réactifs et des produits pour trois expériences impliquant cette réaction :

\[\ce{CO}(g)+\ce{H2O}(g) \rightleftharpoons \ce{CO2}(g)+\ce{H2}(g) \nonumber \]

avec\(K_c=0.64 \). Déterminez dans quelle direction se déroule la réaction lorsqu'elle atteint l'équilibre dans chacune des trois expériences présentées.

Réactifs/produits pour trois expériences
Réactifs/Produits	Expérience 1	Expérience 2	Expérience 3
_[CO]	0,0203 M	0,011 M	0,0094 M
_{[H ₂ O]}	0,0203 M	0,0011 M	0,0025 M
_{[CO ₂]}	0,0040 M	0,037 M	0,0015 M
_{[H ₂]}	0,0040 M	0,046 M	0,0076 M

Solution

Expérience 1 :

\[Q_c=\ce{\dfrac{[CO2][H2]}{[CO][H2O]}}=\dfrac{(0.0040)(0.0040)}{(0.0203)(0.0203)}=0.039. \nonumber \]

Q _c <\(K_c\) (0,039 < 0,64)

La réaction se déplacera vers la droite.

Expérience 2 :

\[Q_c=\ce{\dfrac{[CO2][H2]}{[CO][H2O]}}=\dfrac{(0.037)(0.046)}{(0.011)(0.0011)}=1.4 \times 10^2 \nonumber \]

Q _c >\(K_c\) (140 > 0,64)

La réaction se déplacera vers la gauche.

Expérience 3 :

\[Q_c=\ce{\dfrac{[CO2][H2]}{[CO][H2O]}}=\dfrac{(0.0015)(0.0076)}{(0.0094)(0.0025)}=0.48 \nonumber \]

Q _c <\(K_c\) (0,48 < 0,64)

La réaction se déplacera vers la droite.

Exercice\(\PageIndex{3}\)

Calculez le quotient de réaction et déterminez la direction dans laquelle chacune des réactions suivantes se déroulera pour atteindre l'équilibre.

a) Un flacon de 1 L contenant 0,0500 mol de NO (g), 0,0155 mol de Cl ₂ (g) et 0,500 mol de NoCl :

\[\ce{2NO}(g)+\ce{Cl2}(g)⇌\ce{2NOCl}(g)\hspace{20px}K_c=4.6\times 10^4 \nonumber \]

b) Un flacon de 5,0 L contenant 17 g de NH ₃, 14 g de N ₂ et 12 g de H ₂ :

\[\ce{N2}(g)+\ce{3H2}(g)⇌\ce{2NH3}(g)\hspace{20px}K_c=0.060 \nonumber \]

c) Un flacon de 2 L contenant 230 g de SO ₃ (g) :

\[\ce{2SO3}(g)⇌\ce{2SO2}(g)+\ce{O2}(g)\hspace{20px}K_c=0.230 \nonumber \]

Répondez à: \(Q_c\)= 6,45 × 10 ³, se déplace vers la droite.
Réponse b: \(Q_c\)= 0,12, se déplace vers la gauche.
Réponse c: \(Q_c\)= 0, se déplace vers la droite

Dans l'exemple\(\PageIndex{2}\), il a été mentionné que la pratique courante consiste à omettre les unités lors de l'évaluation des quotients de réaction et des constantes d'équilibre. Il convient de souligner que l'utilisation de concentrations dans ces calculs est une approche pratique mais simplifiée qui conduit parfois à des résultats apparemment incompatibles avec la loi de l'action de masse. Par exemple, les équilibres impliquant des ions aqueux présentent souvent des constantes d'équilibre qui varient de manière assez significative (ne sont pas constantes) à des concentrations de solution élevées. Cela peut être évité en calculant\(K_c\) les valeurs en utilisant les activités des réactifs et des produits dans le système d'équilibre au lieu de leurs concentrations. L'activité d'une substance est une mesure de sa concentration effective dans des conditions spécifiées. Bien qu'une discussion détaillée de cette importante quantité dépasse le cadre d'un texte d'introduction, il est nécessaire de prendre conscience de quelques aspects importants :

Les activités sont des quantités adimensionnelles (sans unités) et sont essentiellement des concentrations « ajustées ».
Pour les solutions relativement diluées, l'activité d'un soluté et sa concentration molaire sont à peu près égales.
Les activités des phases condensées pures (solides et liquides) sont égales à 1.
Les activités des solvants dans les solutions diluées sont égales à 1.

En conséquence de ces deux derniers aspects,\(Q_c\) les\(K_c\) expressions ne contiennent pas de termes désignant des solides, des liquides ou des solvants dans des solutions diluées (étant numériquement égaux à 1, ces termes n'ont aucun effet sur la valeur de l'expression). Plusieurs exemples d'équilibres donnant lieu à de telles expressions seront présentés dans cette section.

Équilibres homogènes

Un équilibre homogène est un équilibre dans lequel tous les réactifs et produits sont présents dans une seule solution (par définition, un mélange homogène). Dans ce chapitre, nous nous concentrerons sur les deux types d'équilibres homogènes les plus courants : ceux qui se produisent dans des solutions en phase liquide et ceux impliquant exclusivement des espèces gazeuses. Les réactions entre les solutés dans les solutions liquides appartiennent à un type d'équilibre homogène. Les espèces chimiques impliquées peuvent être des molécules, des ions ou un mélange des deux. Plusieurs exemples sont fournis ici :

Exemple 1

\[\ce{C2H2}(aq)+\ce{2Br2}(aq) \rightleftharpoons \ce{C2H2Br4}(aq)\hspace{20px} \label{13.3.7a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[C2H2Br4]}{[C2H2][Br2]^2}} \label{13.3.7b} \]

Exemple 2

\[\ce{I2}(aq)+\ce{I-}(aq) \rightleftharpoons \ce{I3-}(aq) \label{13.3.8b} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[I3- ]}{[I2][I- ]}} \label{13.3.8c} \]

Exemple 3

\[\ce{Hg2^2+}(aq)+\ce{NO3-}(aq)+\ce{3H3O+}(aq) \rightleftharpoons \ce{2Hg^2+}(aq)+\ce{HNO2}(aq)+\ce{4H2O}(l) \label{13.3.9a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[Hg^2+]^2[HNO2]}{[Hg2^2+][NO3- ][H3O+]^3}} \label{13.3.9b} \]

Exemple 4

\[\ce{HF}(aq)+\ce{H2O}(l) \rightleftharpoons \ce{H3O+}(aq)+\ce{F-}(aq) \label{13.3.10a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[H3O+][F- ]}{[HF]}} \label{13.3.10b} \]

Exemple 5

\[\ce{NH3}(aq)+\ce{H2O}(l) \rightleftharpoons \ce{NH4+}(aq)+\ce{OH-}(aq) \label{13.3.11a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[NH4+][OH- ]}{[NH3]}} \label{13.3.11b} \]

Dans chacun de ces exemples, le système d'équilibre est une solution aqueuse, comme indiqué par les annotations aq sur les formules des solutés. Comme le H ₂ O (l) est le solvant de ces solutions, on lui attribue une activité de 1 et n'apparaît donc pas explicitement sous forme de terme dans l'\(K_c\)expression, comme indiqué précédemment, même s'il peut également apparaître sous forme de réactif ou de produit dans l'équation chimique.

Les réactions dans lesquelles tous les réactifs et produits sont des gaz constituent une deuxième classe d'équilibres homogènes. Nous utilisons des concentrations molaires dans les exemples suivants, mais nous verrons sous peu que les pressions partielles des gaz peuvent également être utilisées :

Exemple 1

\[\ce{C2H6}(g) \rightleftharpoons \ce{C2H4}(g)+\ce{H2}(g) \label{13.3.12a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[C2H4][H2]}{[C2H6]}} \label{13.3.12b} \]

Exemple 2

\[\ce{3O2}(g) \rightleftharpoons \ce{2O3}(g) \label{13.3.13a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[O3]^2}{[O2]^3}} \label{13.3.13b} \]

Exemple 3

\[\ce{N2}(g)+\ce{3H2}(g) \rightleftharpoons \ce{2NH3}(g) \label{13.3.14a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[NH3]^2}{[N2][H2]^3}} \label{13.3.14b} \]

Exemple 4

\[\ce{C3H8}(g)+\ce{5O2}(g) \rightleftharpoons \ce{3CO2}(g)+\ce{4H2O}(g)\label{13.3.15a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[CO2]^3[H2O]^4}{[C3H8][O2]^5}}\label{13.3.15b} \]

Notez que la concentration de\(\ce{H_2O}_{(g)}\) a été incluse dans le dernier exemple car l'eau n'est pas le solvant de cette réaction en phase gazeuse et sa concentration (et son activité) changent.

Chaque fois que des gaz sont impliqués dans une réaction, la pression partielle de chaque gaz peut être utilisée au lieu de sa concentration dans l'équation du quotient de réaction, car la pression partielle d'un gaz est directement proportionnelle à sa concentration à température constante. Cette relation peut être dérivée de l'équation du gaz idéal, où M est la concentration molaire du gaz,\(\dfrac{n}{V}\).

\[\begin{align} PV&=nRT \label{13.3.16} \\[4pt] P &=\left(\dfrac{n}{V}\right)RT \label{13.3.17} \\[4pt] &=MRT \label{13.3.18} \end{align} \]

Ainsi, à température constante, la pression d'un gaz est directement proportionnelle à sa concentration. En utilisant les pressions partielles des gaz, nous pouvons écrire le quotient de réaction pour le système

\[\ce{C2H6}(g) \rightleftharpoons \ce{C2H4}(g)+\ce{H2}(g) \label{13.3.19} \]

en suivant les mêmes directives pour la dérivation d'expressions basées sur la concentration :

\[Q_P=\dfrac{P_{\ce{C2H4}}P_{\ce{H2}}}{P_{\ce{C2H6}}} \label{13.3.20} \]

Dans cette équation, nous utilisons Q _P pour indiquer un quotient de réaction écrit avec les pressions partielles :\(P_{\ce{C2H6}}\) est la pression partielle de C ₂ H ₆ ;\(P_{\ce{H2}}\), la pression partielle de H ₂ ; et\(P_{\ce{C2H6}}\) la pression partielle de C ₂ H ₄. À l'équilibre :

\[K_P=Q_P=\dfrac{P_{\ce{C2H4}}P_{\ce{H2}}}{P_{\ce{C2H6}}} \label{13.3.21} \]

L'indice\(P\) du symbole\(K_P\) désigne une constante d'équilibre dérivée à l'aide de pressions partielles au lieu de concentrations. La constante d'équilibre, K _P, est toujours une constante, mais sa valeur numérique peut différer de la constante d'équilibre trouvée pour la même réaction en utilisant des concentrations.

La conversion entre une valeur pour\(K_c\), une constante d'équilibre exprimée en termes de concentrations, et une valeur pour\(K_P\), une constante d'équilibre exprimée en termes de pressions, est simple (un K ou un Q sans indice peut être soit une concentration soit une pression).

L'équation relative à\(K_c\) et\(K_P\) est dérivée comme suit. Pour la réaction en phase gazeuse :

\[m\ce{A}+n\ce{B} \rightleftharpoons x\ce{C}+y\ce{D} \label{13.3.22} \]

avec

\[ \begin{align} K_P &=\dfrac{(P_C)^x(P_D)^y}{(P_A)^m(P_B)^n} \label{13.3.23} \\[4pt] &=\dfrac{([\ce C]×RT)^x([\ce D]×RT)^y}{([\ce A]×RT)^m([\ce B]×RT)^n} \label{13.3.24} \\[4pt] &=\dfrac{[\ce C]^x[\ce D]^y}{[\ce A]^m[\ce B]^n}×\dfrac{(RT)^{x+y}}{(RT)^{m+n}} \label{13.3.25} \\[4pt] &=K_c(RT)^{(x+y)−(m+n)} \label{13.3.26} \\[4pt] &=K_c(RT)^{Δn} \label{13.3.27} \end{align} \]

La relation entre\(K_c\) et\(K_P\) est

\[ \color{red} K_P=K_c(RT)^{Δn} \label{13.3.28} \]

Dans cette équation, Δn est la différence entre la somme des coefficients des produits gazeux et la somme des coefficients des réactifs gazeux dans la réaction (variation des moles de gaz entre les réactifs et les produits). Pour la réaction en phase gazeuse\(m\ce{A}+n\ce{B} \rightleftharpoons x\ce{C}+y\ce{D}\), nous avons

\[Δn=(x+y)−(m+n) \label{13.3.29} \]

Exemple\(\PageIndex{4}\): Calculation of K_P

Écrivez les équations pour la conversion\(K_c\) de en K _P pour chacune des réactions suivantes :

\(\ce{C2H6}(g) \rightleftharpoons \ce{C2H4}(g)+\ce{H2}(g)\)
\(\ce{CO}(g)+\ce{H2O}(g) \rightleftharpoons \ce{CO2}(g)+\ce{H2}(g)\)
\(\ce{N2}(g)+\ce{3H2}(g) \rightleftharpoons \ce{2NH3}(g)\)
K _c est égal à 0,28 pour la réaction suivante à 900 °C :

\[\ce{CS2}(g)+\ce{4H2}(g) \rightleftharpoons \ce{CH4}(g)+\ce{2H2S}(g) \nonumber \]

Qu'est-ce que K _P à cette température ?

Solution

(a) Δ n = (2) − (1) = 1

K _P =\(K_c\) (RT) ^{Δ n} =\(K_c\) (RT) ¹ =\(K_c\) (RT)

(b) Δ n = (2) − (2) = 0

K _P =\(K_c\) (RT) ^{Δ n} =\(K_c\) (RT) ⁰ = K _c

K _P =\(K_c\) (RT) ^{Δ n} =\(K_c\) (RT) ⁻² =\(\dfrac{K_c}{(RT)^2}\)

d) K _P =\(K_c\) (RT) ^{Δ n} = (0,28) [(0,0821) (1173)] ⁻² = 3,0 × 10 ⁻⁵

Exercice\(\PageIndex{4}\)

Écrivez les équations pour la conversion de\(K_c\) en K _P pour chacune des réactions suivantes, qui se produisent en phase gazeuse :

\(\ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g)\)
\(\ce{N2O4}(g) \rightleftharpoons \ce{2NO2}(g)\)
\(\ce{C3H8}(g)+\ce{5O2}(g) \rightleftharpoons \ce{3CO2}(g)+\ce{4H2O}(g)\)
À 227 °C, la réaction suivante a\(K_c\) = 0,0952 :

\[\ce{CH3OH}(g) \rightleftharpoons \ce{CO}(g)+\ce{2H2}(g) \nonumber \]

Quelle serait la valeur de K _P à cette température ?

Répondez à: K _P =\(K_c\) (RT) ⁻¹
Réponse b: K _P =\(K_c\) (RT)
Réponse c: K _P =\(K_c\) (RT) ;
Réponse d: 160 ou 1,6 × 10 ²

Équilibres hétérogènes

Un équilibre hétérogène est un système dans lequel les réactifs et les produits se trouvent en deux phases ou plus. Les phases peuvent être n'importe quelle combinaison de phases solides, liquides ou gazeuses et de solutions. Lorsque vous traitez de ces équilibres, n'oubliez pas que les solides et les liquides purs n'apparaissent pas dans des expressions constantes d'équilibre (les activités des solides purs, des liquides purs et des solvants sont de 1).

Certains équilibres hétérogènes impliquent des modifications chimiques :

Exemple 1

\[\ce{PbCl2}(s) \rightleftharpoons \ce{Pb^2+}(aq)+\ce{2Cl-}(aq) \label{13.3.30a} \]

avec constante d'équilibre associée

\[K_c=\ce{[Pb^2+][Cl- ]^2} \label{13.3.30b} \]

Exemple 1

\[\ce{CaO}(s)+\ce{CO2}(g) \rightleftharpoons \ce{CaCO3}(s) \label{13.3.31a} \]

avec constante d'équilibre associée

\[K_c=\dfrac{1}{[\ce{CO2}]} \label{13.3.31b} \]

Exemple 1

\[\ce{C}(s)+\ce{2S}(g) \rightleftharpoons \ce{CS2}(g) \label{13.3.32a} \]

avec constante d'équilibre associée

\[K_c=\ce{\dfrac{[CS2]}{[S]^2}} \label{13.3.32b} \]

D'autres équilibres hétérogènes impliquent des changements de phase, par exemple l'évaporation du brome liquide, comme le montre l'équation suivante :

\[\ce{Br2}(l) \rightleftharpoons \ce{Br2}(g) \label{13.3.33a} \]

avec constante d'équilibre associée

\[K_c=[\ce{Br2}] \label{13.3.33b} \]

Nous pouvons écrire des équations pour les quotients de réaction d'équilibres hétérogènes impliquant des gaz, en utilisant des pressions partielles plutôt que des concentrations. Deux exemples sont les suivants :

\[\ce{CaO}(s)+\ce{CO2}(g) \rightleftharpoons \ce{CaCO3}(s)\label{13.3.34a} \]

avec constante d'équilibre associée

\[K_P=\dfrac{1}{P_{\ce{CO2}}} \label{13.3.34b} \]

\[\ce{C}(s)+\ce{2S}(g) \rightleftharpoons \ce{CS2}(g)\label{13.3.35a} \]

avec constante d'équilibre associée

\[K_P=\dfrac{P_{\ce{CS2}}}{(P_{\ce S})^2} \label{13.3.35b} \]

Résumé

Pour toute réaction à l'équilibre, le quotient de réaction Q est égal à la constante d'équilibre K de la réaction. Si un réactif ou un produit est un solide pur, un liquide pur ou le solvant dans une solution diluée, la concentration de ce composant n'apparaît pas dans l'expression de la constante d'équilibre. À l'équilibre, les valeurs des concentrations des réactifs et des produits sont constantes. Leurs valeurs particulières peuvent varier en fonction des conditions, mais la valeur du quotient de réaction sera toujours égale à K (K _c pour les concentrations ou K _P pour les pressions partielles).

Un équilibre homogène est un équilibre dans lequel tous les composants sont dans la même phase. Un équilibre hétérogène est un équilibre dans lequel les composants se trouvent en deux phases ou plus. Nous pouvons déterminer si une réaction est à l'équilibre en comparant le quotient de réaction à la constante d'équilibre de la réaction.

Équations clés

\(Q=\dfrac{[\ce C]^x[\ce D]^y}{[\ce A]^m[\ce B]^n}\hspace{20px}\textrm{where }m\ce A+n\ce B⇌x\ce C+y\ce D\)
\(Q_P=\dfrac{(P_C)^x(P_D)^y}{(P_A)^m(P_B)^n}\hspace{20px}\textrm{where }m\ce A+n\ce B⇌x\ce C+y\ce D\)
P = MRT
K _P =\(K_c\) (RT) ^{Δ n}

Lexique

constante d'équilibre (K): valeur du quotient de réaction pour un système à l'équilibre

équilibres hétérogènes: équilibres entre les réactifs et les produits dans les différentes phases

équilibres homogènes: équilibres au sein d'une seule phase

K _c: constante d'équilibre pour les réactions basées sur les concentrations de réactifs et de produits

K _P: constante d'équilibre pour les réactions en phase gazeuse basée sur les pressions partielles des réactifs et des produits

loi de l'action de masse: lorsqu'une réaction réversible a atteint l'équilibre à une température donnée, le quotient de réaction reste constant

quotient de réaction (Q): rapport entre le produit des concentrations molaires (ou pressions) des produits et celui des réactifs, chaque concentration (ou pression) étant portée à la puissance égale au coefficient de l'équation

Objectifs d'apprentissage

Exemple\(\PageIndex{1}\): Writing Reaction Quotient Expressions

Solution

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Evaluating a Reaction Quotient

Solution

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Predicting the Direction of Reaction

Solution

Exercice\(\PageIndex{3}\)

Équilibres homogènes

Exemple\(\PageIndex{4}\): Calculation of KP

Solution

Exercice\(\PageIndex{4}\)

Équilibres hétérogènes

Résumé

Équations clés

Lexique

Exemple\(\PageIndex{4}\): Calculation of K_P