Skip to main content
Global

13.0 : Prélude à l'équilibre

  1. Last updated
  2. Save as PDF
  • Page ID
    194029

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Imaginez une plage peuplée de baigneurs et de baigneurs. Lorsque ceux qui se prélassent au soleil font trop chaud et veulent se rafraîchir, ils se lancent dans les vagues pour nager. Alors que les nageurs se fatiguent, ils se dirigent vers la plage pour se reposer. Si ces deux taux de transfert (les baigneurs entrent dans l'eau et les nageurs quittent l'eau) sont égaux, le nombre de baigneurs et de nageurs serait constant ou équilibré, bien que l'identité des personnes change constamment d'un bain de soleil à l'autre et vice versa. Une situation analogue se produit dans les réactions chimiques. Les réactions peuvent se produire simultanément dans les deux sens (réactifs vers les produits et produits vers les réactifs) et atteindre finalement un état d'équilibre.

    Figure\(\PageIndex{1}\) : Le mouvement du dioxyde de carbone à travers les tissus et les cellules sanguines implique plusieurs réactions d'équilibre.
    Une image représente trois carrés bruns, placés côte à côte dans le coin supérieur gauche. Deux des mêmes carrés se trouvent également côte à côte dans le coin inférieur droit. Chaque carré comporte un point noir au centre. L'un des carrés est étiqueté « indice C O 2 » et comporte une double flèche pointant vers une structure en forme de tube rouge qui passe entre les carrés de l'image, du coin supérieur droit au coin inférieur gauche. Cette flèche est étiquetée « C O indice 2 dissous dans le plasma ». Le tube rouge comporte deux formes rondes rouges, et la partie supérieure est étiquetée « C O indice 2 transporté dans les globules rouges ». Les espaces entre les carrés et le tube rouge sont de couleur bleu clair. L'un des carrés situés en haut de l'image est étiqueté « C O indice 2 » et est relié par une double flèche à une équation dans le tube rouge intitulée « C O indice 2, signe plus, H indice 2 O, flèche orientée vers la droite, indice H 2 O, indice H 2 O, indice H 2, indice H 2, indice C O 3, flèche orientée vers la droite, H C O indice 3 signe négatif en exposant, signe plus, signe H en exposant, signe positif. » Le composé « H C O indice 3 signe négatif exposant » est ensuite relié par une double flèche à l'espace du tube rouge et est étiqueté « H C O indice 3 signe négatif exposant dissous dans le plasma sous forme d'acide carbonique ».

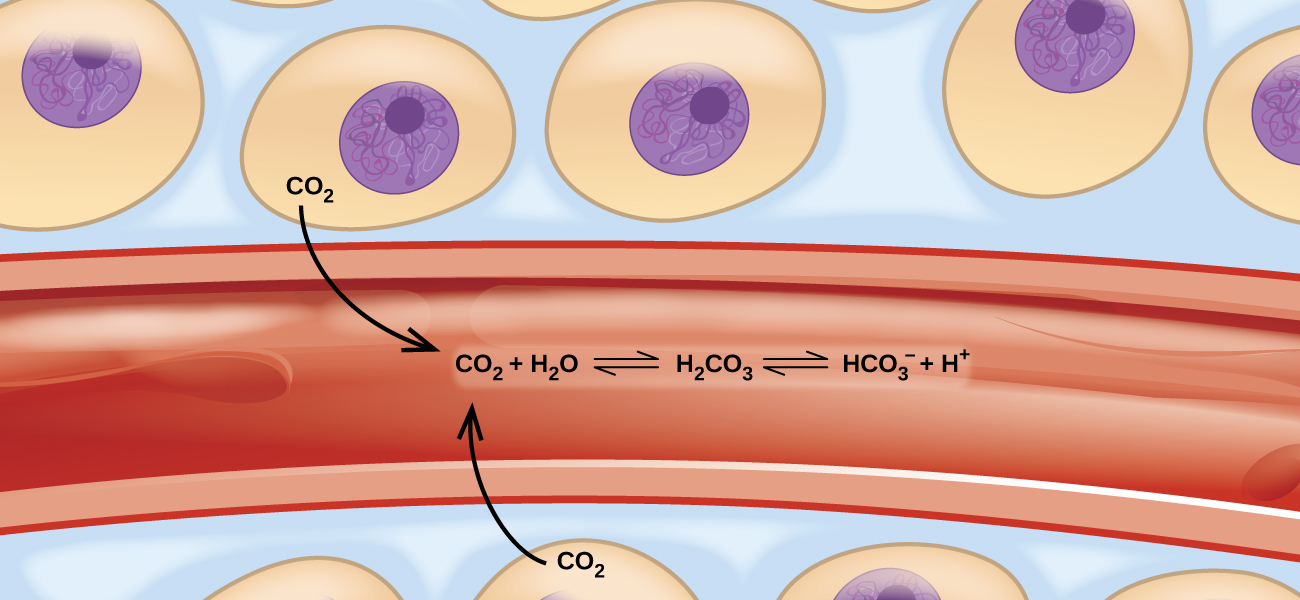
    Ces réactions bidirectionnelles équilibrées se produisent tout autour de nous et même en nous. Par exemple, ils se produisent dans notre sang, où la réaction entre le dioxyde de carbone et l'eau forme de l'acide carbonique\(\ce{(HCO3- )}\) (Figure\(\PageIndex{1}\)). La physiologie humaine est adaptée à la quantité de produits ionisés produits par cette réaction (\(\ce{HCO3-}\)et H +). Dans ce chapitre, vous apprendrez comment prédire la position de la balance et le rendement du produit d'une réaction dans des conditions spécifiques, comment modifier les conditions d'une réaction pour augmenter ou réduire le rendement, et comment évaluer la réaction d'un système d'équilibre aux perturbations.