12.E : Cinétique (exercices)
- Page ID
- 193974
12.1 : Taux de réaction chimique
Q12.1.1
Quelle est la différence entre le taux moyen, le taux initial et le taux instantané ?
- Solution
-
Tout d'abord, une vitesse de réaction générale doit être définie pour connaître toute variation d'une vitesse. La vitesse de réaction est définie comme la mesure de la variation de la concentration des réactifs ou des produits par unité de temps. La vitesse d'une réaction chimique n'est pas constante ; elle change plutôt continuellement et peut être influencée par la température. La vitesse d'une réaction peut être définie comme la disparition de tout réactif ou l'apparition d'un produit. Ainsi, une vitesse moyenne est la vitesse de réaction moyenne sur une période donnée de la réaction, la vitesse instantanée est la vitesse de réaction à un moment donné donné de la réaction et la vitesse initiale est la vitesse instantanée au tout début de la réaction (lorsque le produit commence à se former).
La vitesse instantanée d'une réaction peut être désignée comme\[ \lim_{\Delta t \rightarrow 0} \dfrac{\Delta [concentration]}{\Delta t} \nonumber \]
Q12.1.2
L'ozone se décompose en oxygène selon l'équation\(\ce{2O3}(g)⟶\ce{3O2}(g)\). Écrivez l'équation qui relie les expressions de vitesse de cette réaction en termes de disparition de O 3 et de formation d'oxygène.
- Solution
-
Pour la réaction générale, aA —> bB, la vitesse de la réaction peut être exprimée en termes de disparition de A ou d'apparition de B sur une certaine période de temps comme suit.
\[- \dfrac{1}{a}\dfrac{\Delta [A]}{\Delta t} = - \dfrac{1}{b}\dfrac{\Delta [B]}{\Delta t} = \dfrac{1}{c}\dfrac{\Delta [C]}{\Delta t} = \dfrac{1}{d}\dfrac{\Delta [D]}{\Delta t}\]
Nous voulons que la vitesse d'une réaction soit positive, mais la variation de la concentration d'un réactif, A, sera négative car il est utilisé pour être transformé en produit, B. Par conséquent, lorsque l'on exprime la vitesse de la réaction en termes de variation de la concentration de A, il est important d'ajouter un signe négatif à l'avant pour garantir un taux global positif.
Enfin, la vitesse doit être normalisée en fonction de la stœchiométrie de la réaction. Lors de la décomposition de l'ozone en oxygène, deux moles d'ozone forment trois moles d'oxygène gazeux. Cela signifie que l'augmentation de l'oxygène gazeux sera 1,5 fois plus importante que la diminution de l'ozone. Comme la vitesse de la réaction devrait permettre de décrire les deux espèces, nous divisons le changement de concentration par son coefficient stœchiométrique dans l'équation de réaction équilibrée pour résoudre ce problème.
Par conséquent, la vitesse de réaction de décomposition de l'ozone en oxygène gazeux peut être décrite comme suit :
\[Rate=-\frac{Δ[O3]}{2ΔT}=\frac{Δ[O2]}{3ΔT}\]
- Réponse
-
$Rate=- \ frac {Δ [O3]} {2ΔT} = \ frac {Δ [O2]} {3ΔT} \]
Q12.1.3
Dans l'industrie nucléaire, le trifluorure de chlore est utilisé pour préparer l'hexafluorure d'uranium, un composé volatil de l'uranium utilisé pour la séparation des isotopes de l'uranium. Le trifluorure de chlore est préparé par réaction\(\ce{Cl2}(g)+\ce{3F2}(g)⟶\ce{2ClF3}(g)\). Écrivez l'équation qui relie les expressions de vitesse de cette réaction en termes de disparition de Cl 2 et de F 2 et de formation de ClF 3.
- Solution
-
Dans ce problème, on nous demande d'écrire l'équation qui relie les expressions de vitesse en termes de disparition des réactifs de l'équation et en termes de formation du produit. Une vitesse de réaction donne un aperçu de la manière dont la vitesse est affectée en fonction de la concentration des substances dans l'équation. Les taux peuvent souvent être exprimés sur des graphiques de concentration en fonction du temps exprimés en variation (\({\Delta}\)) de concentration et de temps et, dans un intervalle de temps suffisamment court, le taux instantané peut être approximé. Si nous analysions la réaction donnée, le graphique démontrerait que le Cl 2 diminue, que le F 2 diminue 3 fois plus rapidement, puis que le ClF 3 augmente à un rythme doublé. Les réactifs sont utilisés et convertis en produit de sorte qu'ils diminuent au fur et à mesure que les produits augmentent.
Pour ce problème, nous pouvons appliquer la formule générale d'un taux aux aspects spécifiques d'un problème où la forme générale est la suivante :\[aA+bB⟶cC+dD\nonumber \].
Et le taux peut alors être écrit comme suit\(rate=-\frac {1}{a}\frac{{\Delta}[A]}{{\Delta}t}\)\(=-\frac {1}{b}\frac{{\Delta}[B]}{{\Delta}t}\)\(=\frac {1}{c}\frac{{\Delta}[C]}{{\Delta}t}\)\(=\frac {1}{d}\frac{{\Delta}[D]}{{\Delta}t}.\) : Ici, les signes négatifs sont utilisés pour conserver la convention qui consiste à exprimer les taux sous forme de nombres positifs.
Dans ce cas précis, nous utilisons la stœchiométrie pour obtenir les taux spécifiques de disparition et de formation (revenons à ce qui a été dit dans le premier paragraphe). Donc, le problème consiste simplement à se référer à l'équation et à ses coefficients équilibrés. Sur la base de l'équation, nous voyons que le Cl 2 est un réactif et n'a pas de coefficient, que le F 2 a un coefficient de 3 et est également épuisé, puis que le ClF 3 est un produit qui augmente deux fois avec un coefficient de 2. Ainsi, le taux ici peut être écrit comme suit :\[rate=-\frac{{\Delta}[Cl_2]}{{\Delta}t}=-\frac {1}{3}\frac{{\Delta}[F_2]}{{\Delta}t}=\frac {1}{2}\frac{{\Delta}[ClF_3]}{{\Delta}t}\nonumber \]
- Réponse
-
\[\ce{rate}=+\dfrac{1}{2}\dfrac{Δ[\ce{CIF3}]}{Δt}=−\dfrac{Δ[\ce{Cl2}]}{Δt}=−\dfrac{1}{3}\dfrac{Δ[\ce{F2}]}{Δt}\nonumber \]
Q12.1.4
Une étude de la vitesse de dimérisation du C 4 H 6 a donné les données présentées dans le tableau :
\[\ce{2C4H6⟶C8H12}\nonumber \]
| Heure (s) | 0 | 1600 | 3200 | 4800 | 6200 |
|---|---|---|---|---|---|
| [C 4 H 6] (M) | 1,00 × 10 −2 | 5,04 × 10 −3 | 3,37 × 10 −3 | 2,53 × 10 −3 | 2,08 × 10 −3 |
- Déterminez le taux moyen de dimérisation entre 0 s et 1600 s, et entre 1600 s et 3200 s.
- Estimez le taux instantané de dimérisation à 3200 s à partir d'un graphique du temps en fonction de [C 4 H 6]. Quelles sont les unités de ce tarif ?
- Déterminer la vitesse moyenne de formation de C 8 H 12 à 1600 s et la vitesse instantanée de formation à 3200 s à partir des vitesses trouvées dans les parties (a) et (b).
- Solution
-
1.) Le taux moyen de dimérisation est la variation de la concentration d'un réactif par unité de temps. Dans ce cas, ce serait :
\(rate\)\(of\)\(dimerization=-\frac{\Delta [C_4H_6]}{\Delta t}\)
Taux de dimérisation entre 0 s et 1600 s :
\(rate\)\(of\)\(dimerization=-\frac{5.04×10^{-3}M-1.00×10^{-2}M}{1600 s-0 s}\)
\(rate\)\(of\)\(dimerization=3.10 × 10^{-6} \frac{M}{s}\)
Taux de dimérisation entre 1600 s et 3200 s :
\(rate\)\(of\)\(dimerization=-\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(rate\)\(of\)\(dimerization=1.04 × 10^{-6} \frac{M}{s}\)
2.) Le taux instantané de dimérisation à 3200 s peut être déterminé en représentant graphiquement le temps par rapport à [C 4 H 6].
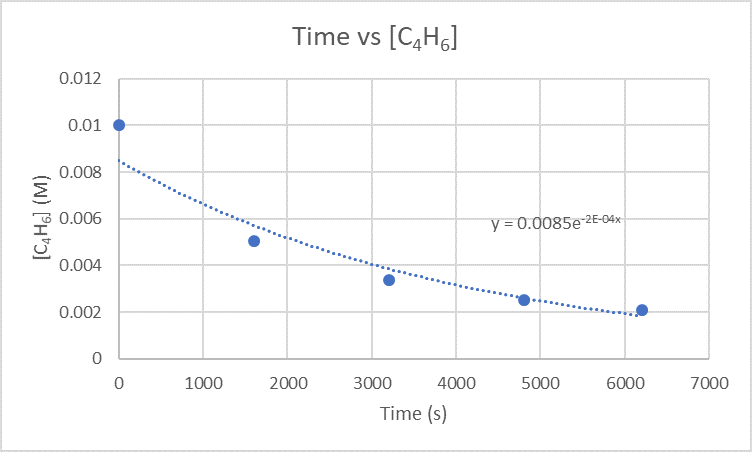
Comme vous voulez trouver le taux de dimérisation à 3200 s, vous devez trouver la pente entre 1600 s et 3200 s et également entre 3200 s et 4800 s.
Pour la pente comprise entre 1600 s et 3200 s, utilisez les points (1600 s, 5,04 x 10 -3 M) et (3200 s, 3,37 x 10 -3 M)
\(\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(\frac{-0.00167 M}{1600 s}\)
\(-1.04×10^{-6}\frac{M}{s}\)
Pour la pente comprise entre 3200 s et 4 800 s, utilisez les points (3200 s, 3,37 x 10 -3 M) et (4800 s, 2,53 x 10 -3 M)
\(\frac{2.53×10^{-3}M-3.37×10^{-3}M}{4800 s-3200 s}\)
\(\frac{-8.4×10^{-4} M}{1600 s}\)
\(-5.25×10^{-7}\frac{M}{s}\)
Prenez les deux pentes que vous venez de trouver et déterminez leur moyenne pour obtenir le taux de dimérisation instantané.
\(\frac{-1.04×10^{-6}\frac{M}{s}+-5.25×x10^{-7}\frac{M}{s}}{2}\)
\(\frac{-1.565×10^{-6}\frac{M}{s}}{2}\)
\(-7.83×10^-7\frac{M}{s}\)
Le taux instantané de dimérisation est \(-7.83×10^-7\frac{M}{s}\)et les unités de ce taux sont \(\frac{M}{s}\).
3.) Le taux moyen de formation de C 8 H 12 à 1600 s et le taux instantané de formation à 3 200 s peuvent être déterminés en utilisant nos réponses des parties a et b. Si vous regardez l'équation initiale, vous pouvez voir que C 4 H 6 et C 8 H 12 sont liés dans un rapport de deux pour un. Pour deux moles de C 4 H 6 utilisées, une mole de C 8 H 12 est produite.
Pour cette réaction, le taux moyen de dimérisation et le taux moyen de formation peuvent être liés par cette équation :
\(\frac{-1}{2}\frac{\Delta [C_4H_6]}{\Delta t}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
Notez que le côté réactif est négatif car les réactifs sont utilisés dans la réaction.
Donc, pour le taux moyen de formation de C 8 H 12 à 1600 s, utilisez le taux de dimérisation entre 0 s et 1600 s que nous avons trouvé précédemment et insérez l'équation suivante :
\(\frac{-1}{2}×3.10 × 10^{-6} \frac{M}{s}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
\(\frac{\Delta [C_8H_{12}]}{\Delta t}=1.55×10^{-6}\frac{M}{s}\)
Le taux moyen de formation du C 8 H 12 à 1600 s est de\(1.55×10^{-6}\frac{M}{s}\). Le taux de formation sera positif car des produits se forment.
La vitesse instantanée de formation de C 8 H 12 peut être liée à la vitesse instantanée de dimérisation par cette équation :
\(\frac{-1}{2}\frac{d[C_4H_6]}{dt}=\frac{d[C_8H_{12}]}{dt}\)
Ainsi, pour le taux instantané de formation du C 8 H 12 à 3 200 s, utilisez la valeur du taux instantané de dimérisation à 3 200 s trouvée plus tôt et inscrivez l'équation :
\(\frac{-1}{2}×-7.83×10^-7\frac{M}{s}=\frac{d[C_8H_{12}]}{dt}\)
\(\frac{d[C_8H_{12}]}{dt}=-3.92×10^{-7}\frac{M}{s}\)
La vitesse instantanée de formation du C 8 H 12 à 3200 s est\(-3.92×10^-7\frac{M}{s}\)
- Réponse
-
- \(3.10 × 10^{-6} \frac{M}{s}\)et\(1.04 × 10^{-6} \frac{M}{s}\)
- \(-7.83×10^-7\frac{M}{s}\)et\(\frac{M}{s}\)
- \(-3.92×10^-7\frac{M}{s}\)
Q12.1.5
Une étude de la vitesse de la réaction représentée\(2A⟶B\) a donné les données suivantes :
| Heure (s) | 0,0 | 5,0 | 10,0 | 15,0 | 20,0 | 25,0 | 35,0 |
|---|---|---|---|---|---|---|---|
| [A] (M) | 1,00 | 0,952 | 0,625 | 0,465 | 0,370 | 0,308 | 0,230 |
- Déterminez le taux moyen de disparition de A entre 0,0 s et 10,0 s et entre 10,0 s et 20,0 s.
- Estimez le taux instantané de disparition de A à 15,0 s à partir d'un graphique du temps par rapport à [A]. Quelles sont les unités de ce tarif ?
- Utilisez les vitesses trouvées dans les parties (a) et (b) pour déterminer la vitesse moyenne de formation de B entre 0,00 s et 10,0 s, et la vitesse instantanée de formation de B à 15,0 s.
- Solution
-
Équations :\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) et Rate=\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\)
Résolvez : 1.) Le changement de A de 0 à 10 s est de 0,625-1 = -0,375 donc\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) = 0,375/10 = 0,0374 m/s
De même, le changement de A de 10 à 20 secondes est de 0,370 à 0,625 = -0,255 donc\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) = 0,255/20-10 = 0,0255 m/s
2.) Nous pouvons estimer la loi des taux en traçant les points par rapport à différentes équations d'ordre afin de déterminer le bon ordre.
Ordre zéro :\[\frac{d[A]}{dt}=-k\nonumber \]\[\int_{A_{\circ}}^{A}d[A]=-k\int_{0}^{t}dt\nonumber \]\[[A]=-kt+[A_{\circ}]\nonumber \]
Première commande :\[\frac{d[A]}{dt}=-k[A]\nonumber \]\[\int_{A_{\circ}}^{A}\frac{d[A]}{[A]}=-kdt\nonumber \]\[Ln(A)=-kt+Ln(A_{\circ})\nonumber \]
Deuxième commande :\[\frac{d[A]}{dt}=-k[A]^{2}\nonumber \]\[\int_{A\circ}^{A}\frac{d[A]}{[A]^{2}}=-k\int_{0}^{t}dt\nonumber \]
\[\frac{1}{[A]}=kt+\frac{1}{[A_{\circ}]}\nonumber \]
Maintenant que nous avons trouvé la forme linéaire de chaque ordre, nous allons tracer les points par rapport à un axe Y [A], un axe Y Ln (A) et un axe y 1/ [A]. Le diagramme qui contient le plus de points linéaires nous donnera une bonne idée de l'ordre et la pente sera la valeur k.
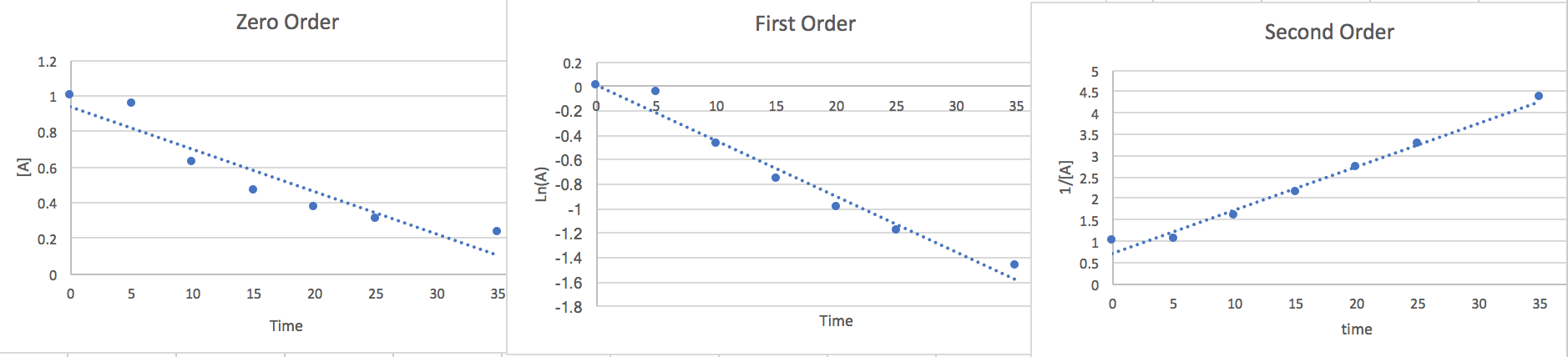
Nous remarquons ici que le deuxième ordre est le plus linéaire, nous concluons donc que le taux est.. \[\frac{-d[A]}{2dt}=k[A]^{2}\nonumber \]À 15 secondes [A] = 0,465 et à partir de la pente du graphique, nous trouvons k = 0,116. Donc, si nous connectons ces données et que nous multiplions les deux côtés par 2 pour éliminer le 2 du dénominateur sur le côté gauche de l'équation, nous trouvons que le taux de disparition de A est de 0,05 m/s où les unités sont équivalentes à [mol*L] -1 [*s -1]
3.) À l'aide de l'équation,\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\) nous divisons les taux des parties a et b par deux pour obtenir 0,0188 m/s entre 0 et 10 secondes et 0,025 m/s pour le taux instantané estimé à 15 secondes.
- Réponse
-
(a) taux moyen, 0 − 10 s = 0,0375 mol L −1 s −1 ; taux moyen, 12 − 18 s = 0,0225 mol L −1 s −1 ; (b) débit instantané, 15 s = 0,0500 mol L −1 s −1 ; (c) taux moyen de formation de B = 0,0188 mol L −1 s −1 ; taux instantané de formation de B = 0,0250 mol L −1 s −1
Q12.1.6
Envisagez la réaction suivante en solution aqueuse :
\[\ce{5Br-}(aq)+\ce{BrO3-}(aq)+\ce{6H+}(aq)⟶\ce{3Br2}(aq)+\ce{3H2O}(l)\nonumber \]
Si la vitesse de disparition du Br — (aq) à un moment donné de la réaction est de 3,5 × 10 −4 M s −1, quelle est la vitesse d'apparition du Br 2 (aq) à ce moment ?
- Solution
-
Étape 1. Définissez la vitesse de la réaction.
Rappel :
Pour la réaction générale : aA + bB → CC+ dD
\(rate =- \frac{\Delta[A]}{a\Delta{t}}=- \frac{\Delta[B]}{b\Delta{t}}= \frac{\Delta[C]}{c\Delta{t}}=\frac{\Delta[D]}{d\Delta{t}}\)
Donc, pour la réaction :\(5Br^−(aq)+BrO^−_3(aq)+6H^+→3Br_2(aq)+3H_2O(l)\)
Le taux serait le suivant :\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}=- \frac{\Delta[BrO^-_3]}{\Delta{t}}= -\frac{\Delta[H^+]}{6\Delta{t}}=\frac{\Delta[Br_2]}{3\Delta{t}}=\frac{H_2O}{3\Delta{t}}\)
Étape 2. Puisque l'on nous donne le taux de disparition de\(Br^-\) (aq) est\(3.5x10^-4 Ms^{-1}\), et nous voulons trouver le taux d'apparition de\(Br_2\) (aq). Nous avons donc fixé les deux taux de manière égale.
\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}= \frac{\Delta[Br_2]}{3\Delta{t}}\)
Et\(-\frac{\Delta[Br^-]}{\Delta{t}}= -3.5x10^{-4} Ms^{-1}\)
Donc,\(3.5x10^{-4} Ms^{-1}\) =\(\frac{5}{3}\frac{\Delta[Br_2]}{\Delta{t}}\)
Étape 3. Maintenant, résolvez l'équation.
\(\frac{(3.5x10^{-4})(3)}{5} = \frac{\Delta[Br_2]}{\Delta{t}}\)
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
- Réponse
-
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
12.2 : Facteurs influant sur les taux de
Q12.2.1
Décrivez l'effet de chacun des éléments suivants sur la vitesse de réaction du magnésium métallique avec une solution d'acide chlorhydrique : la molarité de l'acide chlorhydrique, la température de la solution et la taille des morceaux de magnésium.
- Solution
-
Molarité de l'acide chlorhydrique
- Les vitesses de réaction sont influencées par la fréquence à laquelle les molécules entrent en collision. Molarité élevée = concentration élevée, ce qui signifie qu'un plus grand nombre de molécules sont disponibles pour entrer en collision, ce qui permet une réaction plus rapide qu'une réaction avec une faible molarité de HCl à un volume fixe.
- Des températures plus élevées augmentent la vitesse de réaction, car les molécules se déplacent plus rapidement et entrent donc en collision plus fréquemment.
- l'augmentation des températures permet à un plus grand nombre de particules de franchir la barrière d'énergie d'activation pour démarrer la réaction
- la vitesse de réaction dépend de la taille du réactif solide ; les pièces plus petites augmentent les risques de collision car elles permettent une plus grande surface et donc une vitesse de réaction plus rapide
Q12.2.2
Accédez à la page interactive PhET Reactions & Rates. Utilisez l'onglet Collision unique pour montrer comment la collision entre l'oxygène monatomique (O) et le monoxyde de carbone (CO) entraîne la rupture d'une liaison et la formation d'une autre. Tirez sur le piston rouge pour libérer l'atome et observez les résultats. Cliquez ensuite sur « Recharger le lanceur » et passez à « Plan incliné » pour voir la différence.
- Que se passe-t-il lorsque l'angle de la collision est modifié ?
- Expliquez en quoi cela se rapporte à la vitesse de réaction.
- Solution
-
Selon la théorie des collisions, de nombreux facteurs sont à l'origine d'une réaction, dont trois sont la fréquence à laquelle les molécules ou les atomes entrent en collision, l'orientation des molécules ou des atomes et la question de savoir s'il y a suffisamment d'énergie pour que la réaction se produise. Ainsi, si l'angle du piston est modifié, l'atome qui est projeté (un atome d'oxygène isolé dans ce cas) heurtera l'autre molécule (CO dans ce cas) à un endroit et à un angle différents. Par conséquent, la modification de l'orientation et du nombre de collisions appropriées ne provoquera probablement pas de réaction . Grâce à la simulation, nous pouvons voir que c'est vrai : selon l'angle sélectionné, l'atome peut mettre beaucoup de temps à entrer en collision avec la molécule et, lorsqu'une collision se produit, elle peut ne pas entraîner la rupture de la liaison et la formation de l'autre (aucune réaction ne se produit).
Dans ce cas précis, la vitesse de la réaction diminuera car, en modifiant l'angle, les molécules ou les atomes n'entreront pas en collision avec la bonne orientation ou aussi souvent avec la bonne orientation.
Q12.2.3
Dans l'interface interactive PhET Reactions & Rates, utilisez l'onglet « Nombreuses collisions » pour observer comment plusieurs atomes et molécules interagissent dans différentes conditions. Sélectionnez une molécule à pomper dans la chambre. Réglez la température initiale et sélectionnez les quantités actuelles de chaque réactif. Sélectionnez « Afficher les obligations » sous Options. Comment la vitesse de la réaction est-elle affectée par la concentration et la température ?
ARTICLE 12.2.3
Selon la théorie des collisions, une réaction ne se produira que si les molécules entrent en collision avec une orientation appropriée et avec l'énergie requise pour que la réaction se produise. L'énergie minimale avec laquelle les molécules doivent entrer en collision est appelée énergie d'activation (énergie de l'état de transition).
L'augmentation de la concentration des réactifs augmente la probabilité que les réactifs entrent en collision dans la bonne orientation, car il y a plus de réactifs dans le même volume d'espace. Par conséquent, l'augmentation de la concentration des réactifs augmenterait la vitesse de la réaction. La diminution de la concentration des réactifs diminuerait la vitesse de réaction, car le nombre total de collisions possibles diminuerait.
La température est directement liée à l'énergie cinétique des molécules et l'énergie d'activation\(E_a\) est l'énergie minimale requise pour qu'une réaction se produise et qui ne change pas pour une réaction. L'augmentation de la température augmente l'énergie cinétique des réactifs, ce qui signifie que les réactifs se déplacent plus rapidement et entrent en collision les uns avec les autres plus fréquemment. Par conséquent, l'augmentation de la température augmente la vitesse de la réaction. La diminution de la température diminue la vitesse de réaction car les molécules auront moins d'énergie cinétique, se déplaceront plus lentement et se heurteront donc moins fréquemment.
Q12.2.4
Dans l'interface interactive PhET Reactions & Rates, dans l'onglet Nombreuses collisions, configurez une simulation avec 15 molécules de A et 10 molécules de BC. Sélectionnez « Afficher les obligations » sous Options.
- Conservez le réglage par défaut de la température initiale. Observez la réaction. La vitesse de réaction est-elle rapide ou lente ?
- Cliquez sur « Pause » puis sur « Tout réinitialiser », puis saisissez à nouveau 15 molécules de A et 10 molécules de BC. Sélectionnez « Afficher les obligations » sous Options. Cette fois, augmentez la température initiale jusqu'à ce que, sur le graphique, la ligne d'énergie moyenne totale soit complètement au-dessus de la courbe d'énergie potentielle. Décrivez ce qu'il advient de la réaction.
- Solution
-
a. Lors de la simulation, nous sélectionnons le réglage par défaut et la réaction A+BC. Dans le réglage par défaut, nous constatons des collisions fréquentes, une température initiale basse et une énergie moyenne totale inférieure à l'énergie d'activation. La théorie des collisions indique que la vitesse d'une réaction est directement proportionnelle à (la fraction de molécules ayant l'orientation requise), (fractions de collisions ayant l'énergie requise) et (fréquence des collisions). Bien que nous voyions des réactifs se déplacer et entrer fréquemment en collision, la vitesse de la réaction directe est en fait lente car les produits, AB et C, mettent beaucoup de temps à apparaître. Cela est principalement dû au fait que les fractions de collisions avec l'énergie requise sont faibles, car l'énergie moyenne des molécules est inférieure à l'énergie d'activation.
b. La réaction se déroule à un rythme encore plus rapide. Encore une fois, la théorie des collisions indique que la vitesse d'une réaction est directement proportionnelle à (la fraction de molécules ayant l'orientation requise), (fractions de collisions ayant l'énergie requise) et (fréquence des collisions). Comme les molécules ont une plus grande quantité d'énergie, elles ont plus d'énergie cinétique. Avec une énergie cinétique accrue, les molécules entrent non seulement plus en collision, mais leur fraction de collision augmente également. Cependant, la réaction directe et la réaction arrière se déroulent toutes deux à un rythme rapide, de sorte que les deux se produisent presque simultanément. Il faut moins de temps pour que les deux réactions se produisent. Lorsque les deux réactions s'additionnent dans l'ensemble, il y a finalement un état d'équilibre. Le processus par lequel l'équilibre est atteint est toutefois plus rapide. Par conséquent, la quantité de produits d'A+BC reste la même après un certain temps.
12.3 : Lois tarifaires
Q12.3.1
En quoi la vitesse d'une réaction et sa constante de vitesse diffèrent-elles ?
ARTICLE 12.3.1
La vitesse d'une réaction ou la vitesse de réaction est la variation de la concentration du réactif ou du produit sur une période donnée. Si les concentrations changent, le taux change également.
Tarif pour A → B :
La constante de vitesse (k) est une constante de proportionnalité qui relie les vitesses de réaction aux réactifs. Si les concentrations changent, la constante de vitesse ne change pas.
Pour une réaction avec l'équation générale :\(aA+bB→cC+dD \)
la loi des taux déterminée expérimentalement a généralement la forme suivante :
Q12.3.2
Doubler la concentration d'un réactif multiplie par quatre la vitesse d'une réaction. Forts de ces connaissances, répondez aux questions suivantes :
- Quel est l'ordre de la réaction par rapport à ce réactif ?
- Le fait de tripler la concentration d'un réactif différent multiplie par trois la vitesse d'une réaction. Quel est l'ordre de la réaction par rapport à ce réactif ?
- Solution
-
a) 2 ; b) 1
Q12.3.3
Tripler la concentration d'un réactif multiplie par neuf la vitesse d'une réaction. Forts de ces connaissances, répondez aux questions suivantes :
- Quel est l'ordre de la réaction par rapport à ce réactif ?
- Augmenter la concentration d'un réactif d'un facteur quatre multiplie par quatre la vitesse d'une réaction. Quel est l'ordre de la réaction par rapport à ce réactif ?
Q12.3.4
Dans quelle mesure et dans quelle direction chacun des facteurs suivants influera-t-il sur la vitesse de la réaction :\(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) si la loi de vitesse pour la réaction est\(\ce{rate}=k[\ce{NO2}]^2\) ?
- Diminution de la pression du NO 2 de 0,50 atm à 0,250 atm.
- Augmentation de la concentration de CO de 0,01 M à 0,03 M.
- Solution
-
(a) Le procédé réduit le taux d'un facteur 4. (b) Comme le CO n'apparaît pas dans la loi sur les taux, le taux n'est pas affecté.
Q12.3.5
Comment chacun des facteurs suivants influera-t-il sur la vitesse de la réaction :\(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) si la loi de vitesse de la réaction est la suivante\(\ce{rate}=k[\ce{NO2}][\ce{CO}]\) ?
- Augmentation de la pression du NO 2 de 0,1 atm à 0,3 atm
- Augmentation de la concentration de CO de 0,02 M à 0,06 M.
Q12.3.6
Les vols réguliers d'aéronefs supersoniques dans la stratosphère sont préoccupants car ces aéronefs produisent du monoxyde d'azote (NO) en tant que sous-produit dans les gaz d'échappement de leurs moteurs. L'oxyde nitrique réagit avec l'ozone, et il a été suggéré que cela pourrait contribuer à l'appauvrissement de la couche d'ozone. La réaction\(\ce{NO + O3⟶NO2 + O2}\) est du premier ordre en ce qui concerne à la fois le NO et l'O 3 avec une constante de vitesse de 2,20 × 10 7 L/mol/s. Quelle est la vitesse instantanée de disparition du NO lorsque [NO] = 3,3 × 10 −6 M et [O 3] = 5,9 × 10 −7 M ?
- Solution
-
4,3 × 10 −5 mol/L/s
Q12.3.7
Le phosphore radioactif est utilisé dans l'étude des mécanismes des réactions biochimiques, car les atomes de phosphore sont des composants de nombreuses molécules biochimiques. L'emplacement du phosphore (et l'emplacement de la molécule à laquelle il est lié) peut être détecté à partir des électrons (particules bêta) qu'il produit :
\[\ce{^{32}_{15}P⟶^{32}_{16}S + e-}\nonumber \]
Taux = 4,85 × 10 −2\(\mathrm{day^{-1}\:[^{32}P]}\)
Quel est le taux instantané de production d'électrons dans un échantillon dont la concentration en phosphore est de 0,0033 M ?
Q12.3.8
La constante de vitesse pour la désintégration radioactive du 14 C est de 1,21 × 10 −4 an −1. Les produits de la désintégration sont les atomes d'azote et les électrons (particules bêta) :
\[\ce{^6_{14}C⟶^{6}_{14}N + e-}\nonumber \]
\[\ce{rate}=k[\ce{^6_{14}C}]\nonumber \]
Quel est le taux instantané de production d'atomes d'azote dans un échantillon dont la teneur en carbone 14 est de 6,5 × 10 −9 M ?
- Solution
-
7,9 × 10 −13 mol/L/an
Q12.3.9
Quel est le taux instantané de production d'atomes N Q12.3.8 dans un échantillon ayant une teneur en carbone 14 de 1,5 × 10 −9 M ?
Q12.3.10
La décomposition de l'acétaldéhyde est une réaction du second ordre avec une constante de vitesse de 4,71 × 10 −8 L/mol/s. Quelle est la vitesse instantanée de décomposition de l'acétaldéhyde dans une solution à une concentration de 5,55 × 10 −4 M ?
Q12.3.11
L'alcool est éliminé de la circulation sanguine par une série de réactions métaboliques. La première réaction produit de l'acétaldéhyde, puis d'autres produits se forment. Les données suivantes ont été déterminées pour le taux auquel l'alcool est éliminé du sang d'un homme moyen, bien que les taux individuels puissent varier de 25 à 30 %. Les femmes métabolisent l'alcool un peu plus lentement que les hommes :
| [C 2 H 5 OH] (M) | 4,4 × 10 −2 | 3,3 × 10 −2 | 2,2 × 10 −2 |
|---|---|---|---|
| Taux (mol/L/h) | 2,0 × 10 −2 | 2,0 × 10 −2 | 2,0 × 10 −2 |
Déterminez l'équation de vitesse, la constante de vitesse et l'ordre global de cette réaction.
- Solution
-
taux = k ; k = 2,0 × 10 -2 mol/L/h (environ 0,9 g/L/h pour le mâle moyen) ; La réaction est d'ordre zéro.
Q12.3.12
Dans certaines conditions, la décomposition de l'ammoniac sur une surface métallique donne les données suivantes :
| [NH 3] (M) | 1,0 × 10 −3 | 2,0 × 10 −3 | 3,0 × 10 −3 |
|---|---|---|---|
| Taux (mol/L/h 1) | 1,5 × 10 −6 | 1,5 × 10 −6 | 1,5 × 10 −6 |
Déterminez l'équation de vitesse, la constante de vitesse et l'ordre global de cette réaction.
Q12.3.13
Le chlorure de nitrosyle, NoCl, se décompose en NO et en Cl 2.
\[\ce{2NOCl}(g)⟶\ce{2NO}(g)+\ce{Cl2}(g)\nonumber \]
Déterminez l'équation de vitesse, la constante de vitesse et l'ordre global de cette réaction à partir des données suivantes :
| [Non] (M) | 0,10 | 0,20 | 0,30 |
|---|---|---|---|
| Taux (mol/L/h) | 8,0 × 10 −10 | 3,2 × 10 −9 | 7,2 × 10 −9 |
- Solution
-
Avant de pouvoir déterminer la constante de taux, nous devons d'abord déterminer l'équation de base et l'ordre des taux. L'équation de vitesse de base pour cette réaction, où n est l'ordre de vitesse du NOCl et k est la constante de vitesse, est
\[rate = k[NOCl]^n\nonumber \]
puisque le NOCl est le réactif de la réaction.
Afin de déterminer l'ordre de la réaction, nous devons trouver l'ordre de [NoCl], car c'est le seul réactif de la réaction. Pour ce faire, nous devons examiner comment la vitesse de la réaction change lorsque la concentration de NoCl change.
Lorsque la concentration de [NoCl] double de 0,10 M à 0,20 M, le taux passe de 8,0 x 10 -10 à 3,2 x 10 -9
(3,2 x 10 -9 (mol/l/h))/(8,0 x 10 -10 (mol/l/h)) = 4
nous concluons donc qu'à mesure que [NoCl] double, le taux augmente de 4. Puisque 2 2 = 4, nous pouvons dire que l'ordre de [NoCl] est 2, donc notre loi de taux mise à jour est
\[rate = k[NOCl]^2\nonumber \]
Maintenant que nous avons l'ordre, nous pouvons substituer les premières valeurs expérimentales du tableau donné pour trouver la constante de vitesse, k
(8,0 x 10 -10 (mol/l/h)) = k (0,10 M) 2 donc
\[k= \dfrac{8.0 \times 10^{-10}}{ (0.10\, M)^2} = 8 \times 10^{-8} M^{-1} sec^{-1}\nonumber \]
Nous avons pu trouver les unités de k en utilisant l'ordre des taux, lorsque l'ordre des taux est de 2 unités de k sont M -1 x sec -1
L'équation du taux est donc la suivante : rate = k [NoCl] 2, c'est du second ordre, et k = 8 x 10 -8 M -1 x sec -1
Loi tarifaire globale :\[rate = \underbrace{(8 \times 10^{-8})}_{\text{1/(M x sec)}} [NOCl]^2\nonumber \]
- Réponse
-
débit = k [NOCl] 2 ; k = 8,0 × 10 −8 L/mol/s ; second ordre
Q12.3.14
À partir des données suivantes, déterminez l'équation de vitesse, la constante de vitesse et l'ordre par rapport à A pour la réaction\(A⟶2C\).
| [A] (M) | 1,33 × 10 −2 | 2,66 × 10 −2 | 3,99 × 10 −2 |
|---|---|---|---|
| Taux (mol/L/h) | 3,80 × 10 −7 | 1,52 × 10 −6 | 3,42 × 10 −6 |
- Solution
-
A. À l'aide des données expérimentales, nous pouvons comparer les effets de la variation de [A] sur la vitesse de réaction en reliant les rapports de [A] aux rapports de vitesses
\[ \frac{2.66 \times 10^{-2}}{1.33 \times 10^{-2}} = 2\nonumber \]et\[ \frac{1.52 \times 10^{-6}}{3.8 \times 10^{-7}} = 4\nonumber \]
B. Cela nous permet de savoir que le fait de doubler la concentration de A provoquera le quadruplement de la vitesse de réaction. L'ordre de cette réaction est 2.
C. Nous pouvons maintenant écrire l'équation du taux puisque nous connaissons l'ordre :
\[rate=k[A]^2\nonumber \]
D. En intégrant un ensemble de données expérimentales à notre équation de vitesse, nous pouvons résoudre pour la constante de vitesse, k :
\[3.8 \times 10^{-7} = k \times (1.33 \times 10^{-2})^{2}\nonumber \]
\[k = \frac{3.8 \times 10^{-7}}{1.769 \times 10^{-4}}\nonumber \]
\[k= .00215 M^{-1}s^{-1}\nonumber \]
- Réponse
-
\(k= .00215 M^{-1}s^{-1}\)
2e commande
Q12.3.15
L'oxyde d'azote (II) réagit avec le chlore selon l'équation suivante :
\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g)\nonumber \]
Les vitesses de réaction initiales suivantes ont été observées pour certaines concentrations de réactifs :
| [NON] (mol/L 1) | [Cl 2] (mol/L) | Taux (mol/L/h) |
|---|---|---|
| 0,50 | 0,50 | 1,14 |
| 1,00 | 0,50 | 4,56 |
| 1,00 | 1,00 | 9,12 |
Quelle est l'équation du taux qui décrit la dépendance du taux par rapport aux concentrations de NO et de Cl 2 ? Qu'est-ce que la constante de vitesse ? Quels sont les ordres relatifs à chaque réactif ?
- Solution
-
Pour l'équation générale,
\(aA + bB \rightarrow cC + dD\)
Le taux peut être écrit sous la forme
\(rate = k[A]^{m}[B]^{n}\)où k est la constante de vitesse et m et n sont les ordres de réaction.
Pour notre équation
\(2NO(g) + Cl_{2}(g) \rightarrow 2NOCl(g)\)
le\(rate = k[NO]^{m}[Cl_{2}]^{n}\)
Maintenant, nous devons trouver les ordres de réaction. Les ordres de réaction ne peuvent être déterminés que par des valeurs expérimentales. Nous pouvons comparer deux réactions où l'un des réactifs a la même concentration pour les deux essais et déterminer l'ordre des réactions.
\(\frac{rate_{1}}{rate_{2}}=\frac{[NO]_{1}^{m}[Cl_{2}]_{1}^{n}}{[NO]_{2}^{m}[Cl_{2}]_{2}^{n}}\)
Nous pouvons utiliser les données du tableau fourni. Si nous insérons les valeurs des lignes 1 et 2, nous constatons que les valeurs de la concentration de Cl s'annuleront, ne laissant que les taux et les concentrations de NO.
\(\frac{1.14}{4.56}=\frac{[0.5]^{m}}{[1.0]^{m}}\)
Nous pouvons maintenant résoudre pour m, et nous trouvons que m =2. Cela signifie que l'ordre de réaction pour [NO] est 2.
Nous devons maintenant trouver la valeur de n. Pour ce faire, nous pouvons utiliser la même équation mais avec les valeurs des lignes 2 et 3. Cette fois, la concentration de NO s'annulera.
\(\frac{4.56}{9.12}=\frac{[0.5]^{n}}{[1.0]^{n}}\)
Lorsque nous résolvons pour n, nous trouvons que n = 1. Cela signifie que l'ordre de réaction pour [Cl 2] est 1.
Nous sommes sur le point de terminer notre équation des taux.
\(rate = k[NO]^{2}[Cl_{2}]\)
Enfin, nous pouvons résoudre la constante de vitesse. Pour ce faire, nous pouvons utiliser l'un des essais de l'expérience et intégrer les valeurs du taux et des concentrations de réactifs, puis résoudre pour k.
\(1.14 mol/L/h = k[0.5 mol/L]^{2}[0.5mol/L]\)
\(k=9.12L^{2}mol^{-2}h^{-1}\)
Donc, notre équation de taux finale est la suivante :
\(rate = (9.12 L^{2} mol^{-2}h^{-1})[NO]^{2}[Cl_{2}]\)
*Une erreur courante est d'oublier des unités. Assurez-vous de suivre vos unités tout au long du processus de détermination de votre constante de taux. Soyez prudent car les unités changeront en fonction de l'ordre de réaction.
- Réponse
-
taux = k [NO] 2 [Cl] 2 ; k = 9,12 L 2 mol −2 h −1 ; second ordre dans NO ; premier ordre dans Cl 2
Q12.3.17
L'hydrogène réagit avec le monoxyde d'azote pour former du monoxyde de diazote (gaz hilarant) selon l'équation suivante :
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g)\nonumber \]
Déterminez l'équation de vitesse, la constante de vitesse et les ordres relatifs à chaque réactif à partir des données suivantes :
| [NON] (M) | 0,30 | 0,60 | 0,60 |
|---|---|---|---|
| [H 2] (M) | 0,35 | 0,35 | 0,70 |
| Débit (mol/L/s) | 2,835 × 10 −3 | 1,134 × 10 −2 | 2,268 × 10 −2 |
- Solution
-
Déterminez l'équation de vitesse, la constante de vitesse et les ordres par rapport à chaque réactif.
La constante de vitesse et les commandes peuvent être déterminées par la loi des taux différentiels. La forme générale de la loi du taux différentiel est donnée ci-dessous :
aA + bB + cC ==> produits
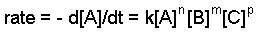
où A, B et C sont les concentrations des réactifs, k est la constante de vitesse et n, m et p se réfèrent à l'ordre de chaque réactif.
Pour déterminer les ordres de chaque réactif, nous voyons que lorsque [NO] double mais que [H 2] ne change pas, la vitesse quadruple, ce qui signifie que [NO] est une réaction du second ordre ([NO] 2). Lorsque [H 2] double mais que [NO] ne change pas, le taux double, ce qui signifie que [H 2] est une réaction de premier ordre. La loi sur les taux ressemblerait donc à ceci :
Taux = k [NO] 2 [H 2]
Nous pouvons utiliser cette loi de vitesse pour déterminer la valeur de la constante de vitesse. Intégrez les données de concentration et de débit des réactifs issues de l'un des essais afin de déterminer pour k la constante de vitesse. Dans ce cas, nous avons choisi d'utiliser les données de l'essai 1 de la deuxième colonne du tableau de données.
2,835 x 10 -3 = k [0,3] 2 [0,35]
k = 0,09 M -2 m/s -1
Q12.3.18
Pour la réaction\(A⟶B+C\), les données suivantes ont été obtenues à 30 °C :
| [A] (M) | 0,230 | 0,356 | 0,557 |
|---|---|---|---|
| Débit (mol/L/s) | 4,17 × 10 −4 | 9,99 × 10 −4 | 2,44 × 10 −3 |
- Quel est l'ordre de la réaction par rapport à [A] et qu'est-ce que l'équation de vitesse ?
- Qu'est-ce que la constante de vitesse ?
- Solution
-
1. L'équation de vitesse pour une réaction d'\(n\)ordre est donnée sous la forme\(\frac{dr}{dt}={k}{[A]^n}\). Où\([A]\) est la concentration en M, et\(\frac{dr}{dt}\) est le taux en m/s.
Nous pouvons ensuite utiliser chaque ensemble de points de données, intégrer ses valeurs dans l'équation du taux et les résoudre\(n\). Notez que vous pouvez utiliser n'importe quel point de données tant que la concentration correspond à son taux.
Équation de taux 1 :\(4.17 \times {10}^{-4}={k}{[0.230]^n}\)
Équation de taux 2 :\(9.99 \times {10}^{-4}={k}{[0.356]^n}\)
Nous divisons l'équation de taux 1 par l'équation de taux 2 afin d'annuler k, la constante de vitesse.
\({\frac{4.17 \times {10}^{-4}}{9.99 \times {10}^{-4}}} = {\frac{k[0.230]^n}{k[0.356]^n}} \)
\({0.417}={0.646^n}\)
Maintenant, la seule inconnue que nous avons est\(n\). En utilisant les règles du logarithme, on peut le résoudre.
\(ln{\: 0.417}={n \cdot ln{\: 0.646}}\)
\(\frac{ln{\: 0.417}}{ln{\:0.646}}=n=2\)
L'équation du taux est du second ordre par rapport à A et s'écrit\(\frac{dr}{dt}={k}{[A]^2}\).
2. Nous pouvons résoudre ce problème\(k\) en insérant n'importe quel point de données dans notre équation de taux\(\frac{dr}{dt}={k}{[A]^2}\).
En utilisant les premiers points de données [par exemple\( [A]=0.230 \:\frac{mol}{L}\)\( \frac{dr}{dt} = 4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}\)], nous obtenons l'équation\(4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}={k}{[0.230 \:\frac{mol}{L}]^2}\)
Ce qui résout\(k=7.88 \times {10}^{-3} \frac{L}{mol \cdot s}\)
Comme nous savons qu'il s'agit d'une réaction de second ordre, les unités appropriées\(k\) peuvent également être écrites sous la forme\( \frac{1}{M \cdot s}\)
- Réponse
-
(a) L'équation du taux est du second ordre en A et s'écrit comme suit : taux = k [A] 2. (b) k = 7,88 × 10 −13 L mol −1 s −1
Q12.3.19
Pour la réaction\(Q⟶W+X\), les données suivantes ont été obtenues à 30 °C :
| [Q] initiale (M) | 0,170 | 0,212 | 0,357 |
|---|---|---|---|
| Débit (mol/L/s) | 6,68 × 10 −3 | 1,04 × 10 −2 | 2,94 × 10 −2 |
- Quel est l'ordre de la réaction par rapport à [Q] et qu'est-ce que l'équation de vitesse ?
- Qu'est-ce que la constante de vitesse ?
- Solution
-
Quel est l'ordre de la réaction par rapport à [Q] et qu'est-ce que l'équation de vitesse ?
- Réaction à l'ordre : 2 car lorsque vous utilisez le ratio d'essai 3:2, cela ressemblera à ceci :
- (\(\dfrac{2.94*10^{-2}}{1.04*10^{-2}}\)) = (\(\dfrac{0.357^{x}}{0.212^{x}}\))
- 2,82 = 1,7 x
- x = 2 donc l'ordre de réaction est 2
- Équation de vitesse de réaction : taux = K [Q] 2
- Pour trouver la constante de vitesse (k), il suffit de brancher et de calculer l'un des essais dans l'équation de vitesse
- 1,04 x 10 -2 =k [0,122] 2
- k = 0,231\(M^{-1}s^{-1}\)
- Réponse
-
Ordre : 2
k = 0,231\(M^{-1}s^{-1}\)
Q12.3.20
La constante de vitesse pour la décomposition du premier ordre à 45 °C du pentoxyde de diazote, N 2 O 5, dissous dans du chloroforme, CHCl 3, est de 6,2 × 10 −4 min −1.
\[\ce{2N2O5⟶4NO2 + O2}\nonumber \]
Quelle est la vitesse de la réaction lorsque [N 2 O 5] = 0,40 M ?
- Solution
-
Étape 1 : La première étape consiste à écrire la loi des taux. Nous connaissons la formule générale d'une loi tarifaire de premier ordre. Il se présente comme suit : Rate=K [A]
Étape 2 : Nous intégrons maintenant [N 2 O 5] pour [A] dans notre loi tarifaire générale. Nous insérons également notre constante de vitesse (k), qui nous a été donnée. Notre équation se présente maintenant comme suit :
Débit = (6,2x10 -4 min -1) [N 2 O 5]
Étape 3 : Nous intégrons maintenant notre molarité donnée. [N 2 O 5] =0,4 M. Notre équation se présente maintenant comme suit :
Débit = (6,2 x 10 -4 min -1) (0,4 M)
Étape 4 : Nous résolvons maintenant notre équation. Taux = (6,2 x 10 -4 min -1) (0,4 M) = 2,48 x 10 -4 m/min.
Étape 5 : Utiliser les chiffres significatifs et la conversion d'unités pour arrondir 2,48 x 10 -4 M/min à 2,5 × 10 −4 (moles) L -1 min -1 min -1
- Réponse
-
a) 2,5 × 10 −4 mol/l/min
Q12.3.21
La production annuelle de HNO 3 en 2013 était de 60 millions de tonnes métriques. La majeure partie de cette production a été préparée par la séquence de réactions suivante, chacune exécutée dans une cuve de réaction séparée.
- \(\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\)
- \(\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\)
- \(\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\)
La première réaction consiste à brûler de l'ammoniac dans de l'air sur un catalyseur au platine. Cette réaction est rapide. La réaction de l'équation (c) est également rapide. La seconde réaction limite la vitesse à laquelle l'acide nitrique peut être préparé à partir d'ammoniac. Si l'équation (b) est du second ordre pour le NO et du premier ordre pour l'O 2, quel est le taux de formation de NO 2 lorsque la concentration en oxygène est de 0,50 M et que la concentration en oxyde nitrique est de 0,75 M ? La constante de vitesse de la réaction est de 5,8 × 10 −6 L 2 /mol 2 /s.
- Solution
-
Pour déterminer la loi de taux d'une équation, nous devons examiner son étape lente. Comme les équations a et c sont toutes deux rapides, l'équation b peut être considérée comme l'étape lente de la réaction. L'étape lente est également considérée comme l'étape déterminante du débit du système.
Par conséquent, l'étape qui détermine le taux est la deuxième étape, car c'est l'étape la plus lente.
taux de production de\(NO_2 = k [A]^m [B]^n \)
\(rate = k [NO]^2 [O_2]^1~M/s\)
\(rate = (5.8*10^{-6}) [0.75]^2 [0.5]^1 ~M/s\)
\(rate = 1.6*10^{-6}~M/s\)
- Réponse
-
\(rate = 1.6*10^{-6}~M/s\)
Q12.3.2
Les données suivantes ont été déterminées pour la réaction :
\[\ce{I- + OCl- ⟶ IO- + Cl-}\nonumber \]
| 1 | 2 | 3 | |
|---|---|---|---|
| \(\mathrm{[I^-]_{initial}}\)(M) | 0,10 | 0,20 | 0,30 |
| \(\mathrm{[OCl^-]_{initial}}\)(M) | 0,050 | 0,050 | 0,010 |
| Débit (mol/L/s) | 3,05 × 10 −4 | 6,20 × 10 −4 | 1,83 × 10 −4 |
Déterminez l'équation de vitesse et la constante de vitesse pour cette réaction.
- Solution
-
À l'aide des réactifs, nous pouvons établir la loi de vitesse de la réaction : $ r=k [OCl^-] ^n [I^-] ^m \]
À partir de là, nous devons utiliser les données pour déterminer l'ordre des deux\([OCl^-]\) et\([I^-]\). Pour ce faire, nous devons effectuer une comparaison\(r_1\) de\(r_2\) telle sorte que :
\[ \frac {r_1}{r_2} = \frac {(0.10^m)(0.050^n)}{(0.20^m)(0.050^n)} = \frac {3.05 \times 10^{-4}}{6.20 \times 10^{-4}} \]
\[ 0.5^m = 0.5 \]
\[ m = 1 \]
Nous pouvons « rayer » la concentration de\([OCl^-]\) parce qu'elle a la même concentration dans les deux essais utilisés.
Maintenant que nous savons que m (\([I^-]\)) a un premier ordre de 1.
Nous ne pouvons pas « rayer »\([I^-]\) pour trouver,\([OCl^-]\) car aucun essai n'a la même concentration. Pour résoudre n, nous allons brancher 1 pour m.
\[ \frac {r_1}{r_3} = \frac {(0.10^{1})(0.050^n)}{(0.30^{1})(0.010^n)} = \frac {3.05 \times 10^{-4}}{1.83 \times 10^{-4}} \]
\[ \frac {1}{3} (5^{n}) = 1.6666667 \]
\[ 5^{n} = 5 \]
\[ n = 1 \]
Comme nous savons que les ordres de n et de m sont égaux à un, nous ne pouvons pas les substituer dans l'équation de la loi de vitesse avec les concentrations respectives (provenant de la première, de la deuxième ou de la troisième réaction) et résoudre la constante de vitesse, k.
\[ r=k[OCl^-]^n[I^-]^m \]
\[ 3.05 * 10^{-4}= k[0.05]^1[0.10]^1 \]
\[ k = 6.1 * 10^{-2} \frac {L}{mol \times s} \]
Ainsi, la loi globale des taux est la suivante : $ r = (6,1 * 10^ {-2} \ frac {L} {mol \ times s}) [OCl^-] [I^-] \]
Les unités de K dépendent de l'ordre général de la réaction. Pour trouver l'ordre global, nous additionnons m et n. En faisant cela, nous trouvons un ordre global de 2. C'est pourquoi les unités de K sont $ \ frac {L} {mol \ times s} \]
- Réponse
-
taux = k [I −] [OCl −1] ; k = 6,1 × 10 −2 L mol −1 s −1
Q12.3.23
Dans la réaction
\[2NO + Cl_2 → 2NOCl\nonumber \]
les réactifs et les produits sont des gaz à la température de la réaction. Les données de taux suivantes ont été mesurées pour trois expériences :
| P {NO} initial | Valeur initiale {Cl 2} | Taux initial |
|---|---|---|
| (guichet automatique) | (guichet automatique) | (moles de A consommées atm sec -1) |
| 0,50 | 0,50 | 5,1 x 10 -3 |
| 1,0 | 1,0 | 4,0 x 10 -2 |
| 0,50 | 1,0 | 1,0 x 10 -2 |
- À partir de ces données, écrivez l'équation de vitesse pour cette réaction gazeuse. Quel est l'ordre de la réaction dans le NO, le Cl 2 et dans l'ensemble ?
- Calculez la constante de vitesse spécifique pour cette réaction.
- Solution
-
a. L'équation de vitesse peut être déterminée en concevant des expériences qui mesurent la concentration d'un ou de plusieurs réactifs ou produits en fonction du temps. Pour la réaction\(A+B\rightarrow products\), par exemple, nous devons déterminer k et les exposants m et n dans l'équation suivante :
\[rate=k[A]^m[B]^n\nonumber \]
Pour ce faire, la concentration initiale de B peut être maintenue constante tout en faisant varier la concentration initiale de A et calcul de la vitesse de réaction initiale. Ces informations déduiraient l'ordre de réaction par rapport à A. Le même processus peut être effectué pour trouver l'ordre de réaction par rapport à B.
Dans cet exemple particulier,
\[\frac{rate_2}{rate_3}=\frac{k[A_2]^m[B_2]^n}{k[A_3]^m[B_3]^n}\nonumber \]
donc en prenant les valeurs du tableau,
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{k[1.0]^m[1.0]^n}{k[0.5]^m[1.0]^n}\nonumber \]
et en annulant des termes similaires, vous vous retrouvez avec
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{[1.0]^m}{[0.5]^m}\nonumber \]
Maintenant, résolvez pour m
\(4=2^m\Longrightarrow m=2\) Parce que m=2, la réaction par rapport à\(NO\) est 2. \(NO\)est de second ordre.
Vous pouvez répéter le même processus pour trouver n.
\[\frac{rate_3}{rate_1}=\frac{k[A_3]^m[B_3]^n}{k[A_1]^m[B_1]^n}\nonumber \]
En prenant les valeurs de la table
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{k[0.5]^m[1.0]^n}{k[0.5]^m[0.5]^n}\nonumber \]
et en annulant les termes similaires, il vous reste
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{[1.0]^n}{[0.5]^n}\nonumber \]
Maintenant, cette fois, résolvez pour n
\(2=2^n\Longrightarrow n=1\)
Parce que n = 1, la réaction par rapport à\(Cl_2\) est 1. \(Cl_2\)est de première commande.
L'équation des taux est donc la suivante :\[rate=k[NO]^2[Cl_2]^1\nonumber \]
Pour trouver l'ordre des taux globaux, il suffit d'additionner les commandes. Le deuxième ordre + le premier ordre fait de la réaction globale un troisième ordre.b. La constante de vitesse est calculée en insérant les données de n'importe quelle ligne du tableau dans la loi de vitesse déterminée expérimentalement et en résolvant k. Pour une réaction du troisième ordre, les unités de k sont\(frac{1}{atm^2*sec}\). En utilisant l'expérience 1,
\[rate=k[NO]^2[Cl_2]^1\Longrightarrow 5.1*10^{-3} \frac{atm}{sec}=k[0.5m atm]^2[0.5 atm]^1\nonumber \]
\[k=0.0408 \frac{1}{atm^2*sec}\nonumber \]
- Réponse
-
\(NO\)est de second ordre.
\(Cl_2\)est de première commande.
L'ordre global des réactions est de trois.
b)
\(k=0.0408\; atm^{-2}*sec^{-1}\)
12.4 : Lois tarifaires intégrées
Q12.4.1
Décrire comment des méthodes graphiques peuvent être utilisées pour déterminer l'ordre d'une réaction et sa constante de vitesse à partir d'une série de données qui incluent la concentration de A à différents moments.
- Solution
-
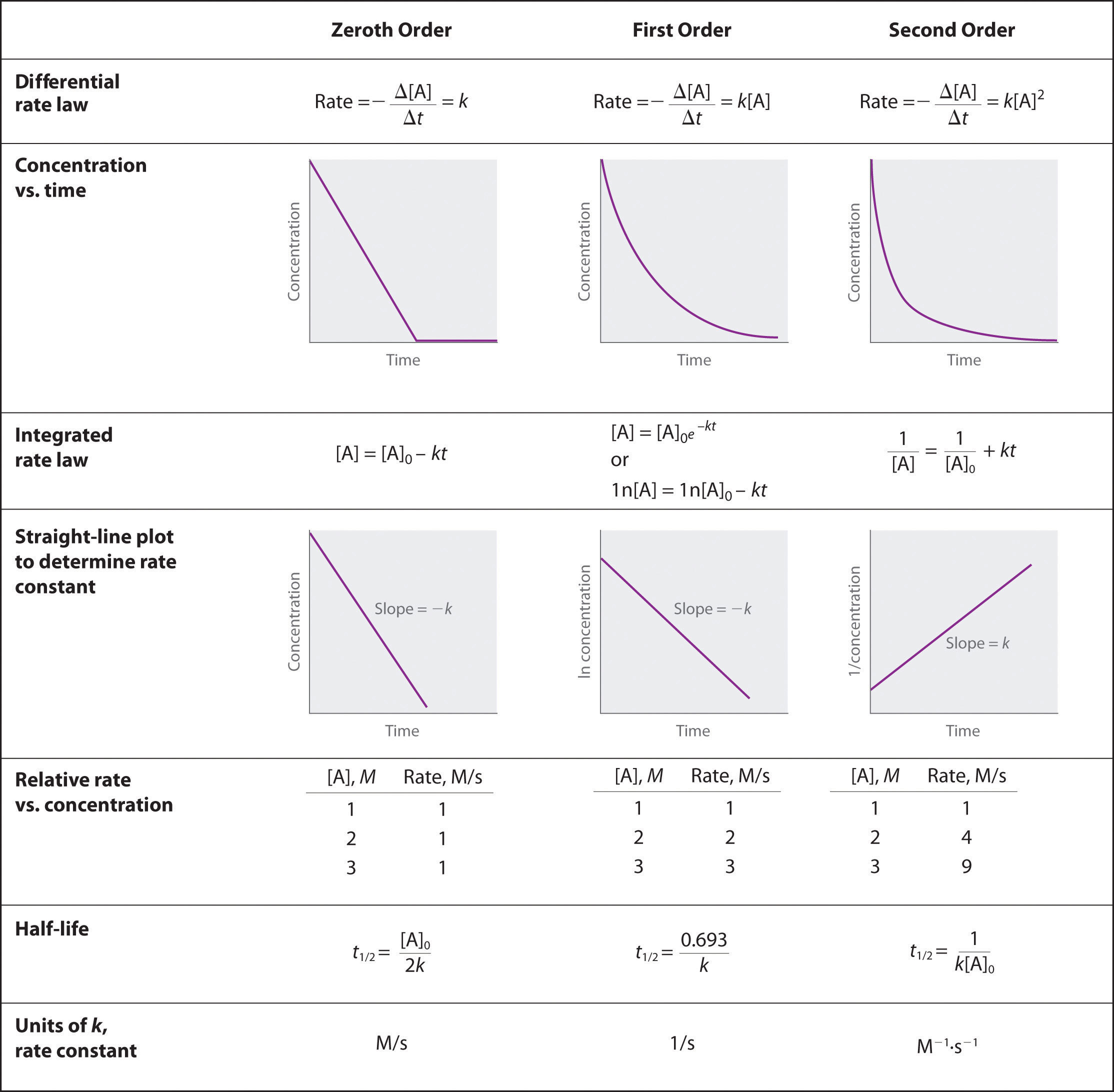
Pour déterminer l'ordre d'une réaction en fonction de la série de données, il faut représenter graphiquement les données, les représenter graphiquement sous la forme d'un logarithme naturel de [A] et les représenter graphiquement comme 1/ [A]. Quelle que soit la méthode qui donne une ligne droite, déterminera l'ordre. Quelles que soient les méthodes de représentation graphique ci-dessus, si une ligne droite est produite par la première méthode graphique, c'est un ordre 0, si par la deuxième méthode c'est un ordre 1, et si la troisième méthode de représentation graphique est un ordre 2. Lorsque l'ordre du graphe est connu, une série d'équations, données dans l'image ci-dessus, peut être utilisée avec les différents points du graphique pour déterminer la valeur de k. Nous pouvons voir que nous avons besoin d'une valeur initiale de A et d'une valeur finale de A, et ces deux valeurs seraient données par les données.
Ordre zéro : lorsque vous tracez la concentration initiale par rapport à la concentration finale, vous avez une pente linéaire négative.
\[[A] = [A]_0 − kt\nonumber \]
Au premier ordre, lorsque vous tracez ln [concentration initiale] par rapport à ln [concentration finale], vous avez une pente linéaire négative.
\[\ln[A] = \ln[A]_0 − kt\nonumber \]
Au second ordre, lorsque vous tracez la 1/ [concentration initiale] par rapport à 1/ [concentration finale], vous obtenez une pente linéaire positive.
\[\dfrac{1}{[\textrm A]}=\dfrac{1}{[\textrm A]_0}+kt\nonumber \]
Q12.4.2
Utilisez les données fournies pour déterminer graphiquement l'ordre et la constante de vitesse de la réaction suivante :\(\ce{SO2Cl2 ⟶ SO2 + Cl2}\)
| Heure (s) | 0 | 5,00 × 10 3 | 1,00 × 10 4 | 1,50 × 10 4 | 2,50 × 10 4 | 3,00 × 10 4 | 4,00 × 10 4 |
|---|---|---|---|---|---|---|---|
| [SO 2 Cl 2] (M) | 0,100 | 0,0896 | 0,0802 | 0,0719 | 0,057 | 0,0517 | 0,0415 |
- Solution
-
Utilisez les données pour déterminer graphiquement l'ordre et la constante de vitesse de la réaction suivante.
Afin de déterminer la loi de vitesse d'une réaction à partir d'un ensemble de données comprenant la concentration (ou les valeurs d'une fonction de concentration) en fonction du temps, créez trois graphes des données en fonction des lois de vitesse intégrées de chaque ordre de réaction.
[concentration] en fonction du temps (linéaire pour une réaction d'ordre zéro) ln [concentration] en fonction du temps (linéaire pour une réaction d'ordre 1) 1/[concentration] en fonction du temps (linéaire pour une réaction d'ordre 2)pente = -2,0 x 10 -5
k = 2,0 x 10 -5
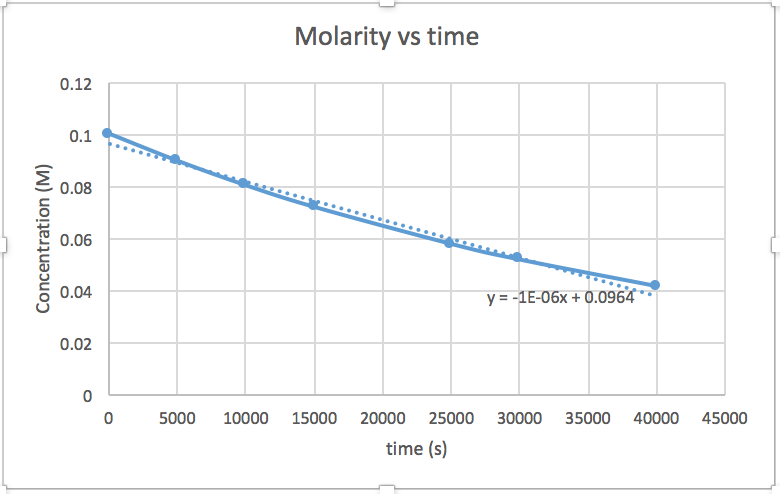
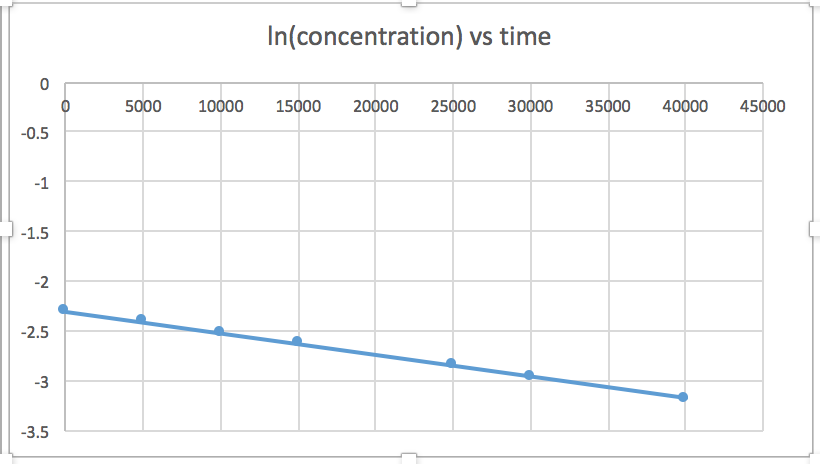
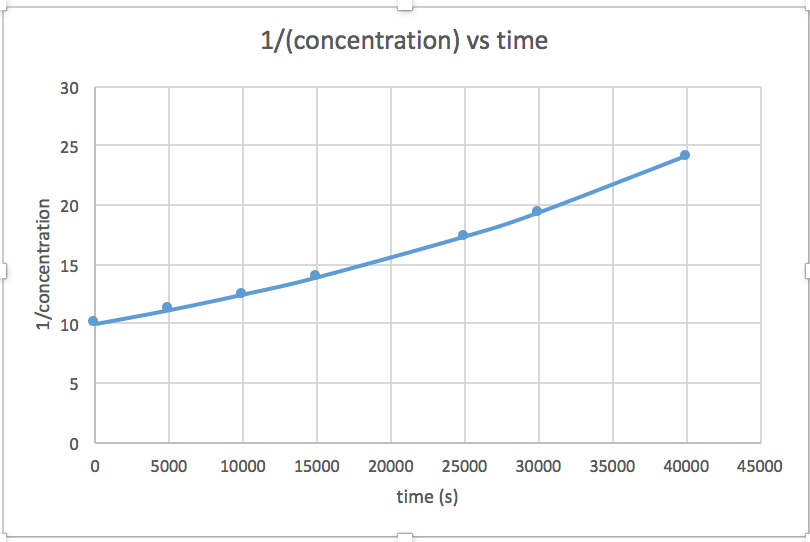
Le graphique linéaire indique l'ordre de la réaction. Ensuite, vous pouvez trouver l'équation de taux correcte :
réaction d'ordre zéro taux = k (k = - pente de la ligne) Réaction du 1 er ordre taux = k [A] (k = - pente de la ligne) Réaction au 2 e ordre taux = k [A] 2 (k = pente de la ligne) Dans ce graphique, ln (concentration) en fonction du temps est linéaire, ce qui indique que la réaction est du premier ordre.
k = pente de la ligne
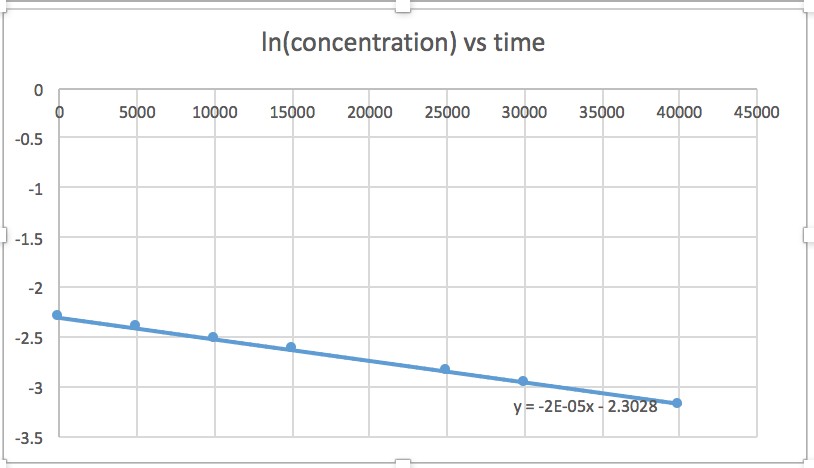
- Réponse
-
Le tracé d'un graphique de ln [SO 2 Cl 2] par rapport à t révèle une tendance linéaire ; nous savons donc qu'il s'agit d'une réaction de premier ordre :
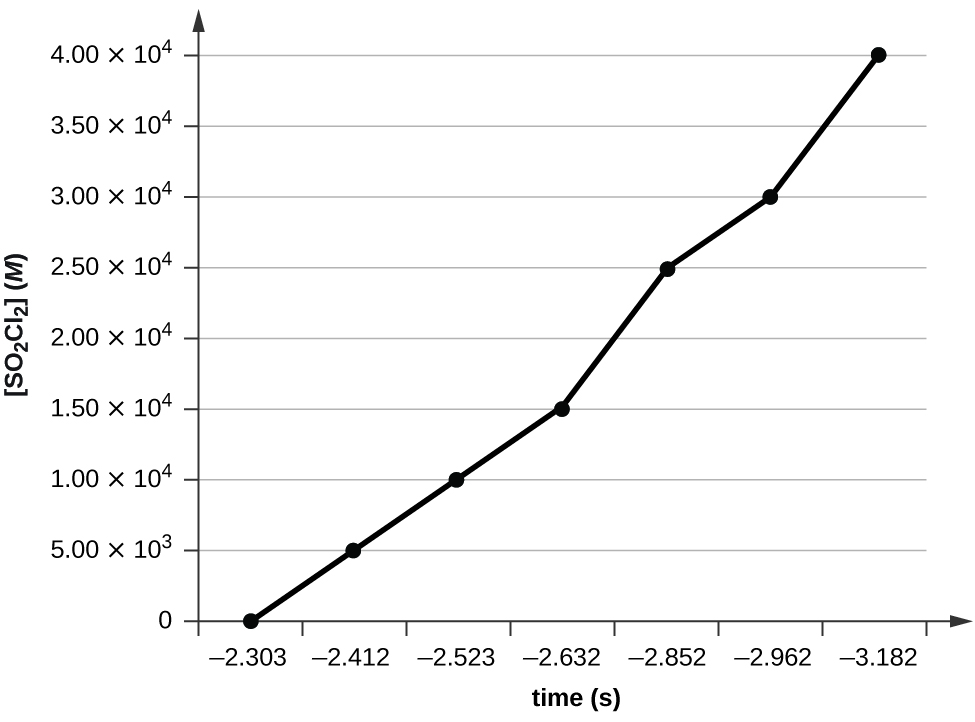
k = −2,20 × 10 5 s −1
Q12.4.3
Utilisez les données fournies dans une méthode graphique pour déterminer l'ordre et la constante de vitesse de la réaction suivante :
\[2P⟶Q+W\nonumber \]
| Heure (s) | 9.0 | 13,0 | 18,0 | 22,0 | 25,0 |
|---|---|---|---|---|---|
| [P] (M) | 1,077 × 10 -3 | 1,068 × 10 −3 | 1,055 × 10 -3 | 1,046 × 10 −3 | 1,039 × 10 −3 |
- Solution
-
Ajoutez des textes ici. Ne supprimez pas ce texte au préalable.
Q12.4.4
L'ozone pur se décompose lentement en oxygène\(\ce{2O3}(g)⟶\ce{3O2}(g)\). Utilisez les données fournies dans une méthode graphique et déterminez l'ordre et la constante de vitesse de la réaction.
| Heure (h) | 0 | 2,0 × 10 3 | 7,6 × 10 3 | 1,23 × 10 4 | 1,70 × 10 4 | 1,70 × 10 4 |
|---|---|---|---|---|---|---|
| [DE 3] (M) | 1,00 × 10 −5 | 4,98 × 10 −6 | 2,07 × 10 −6 | 1,39 × 10 −6 | 1,22 × 10 −6 | 1,05 × 10 −6 |
- Solution
-
Pour déterminer la constante d'ordre et de vitesse, vous devez représenter graphiquement les données d'ordre zéro, de premier ordre et de second ordre en traçant la concentration en fonction du temps- [A] en fonction du temps, le logarithme naturel (ln) de [A] en fonction du temps et 1/ [A] en fonction du temps, respectivement. L'ordre de la réaction est déterminé en identifiant lequel de ces trois graphes produit une ligne droite. La constante de vitesse k est représentée par la pente du graphique. Les graphiques avec leurs valeurs de données respectives seraient
Heure (s) 9.0 13,0 18,0 2,0 25,0 [P] (M) 1,077 × 10−3 1,068 × 10−3 1,055 × 10−3 1,046 × 10−3 1,039 × 10−3 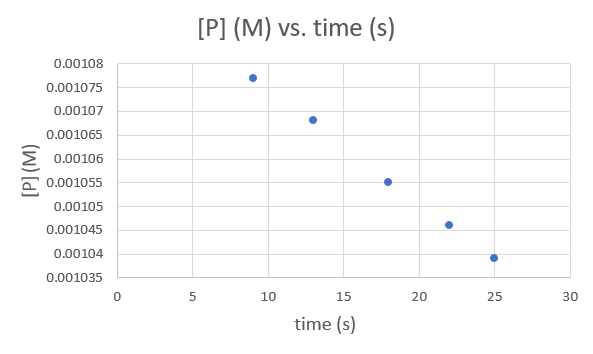.png)
Heure (s) 9.0 13,0 18,0 2,0 25,0 ln [P] (M) -6,83 358 -6,84 197 -6,85 421 -6,86 278 -6,86 95 .png)
Heure (s) 9.0 13,0 18,0 2,0 25,0 1/ [P] (M) 928 5051 936.3296 947 8673 956.0229 962.4639 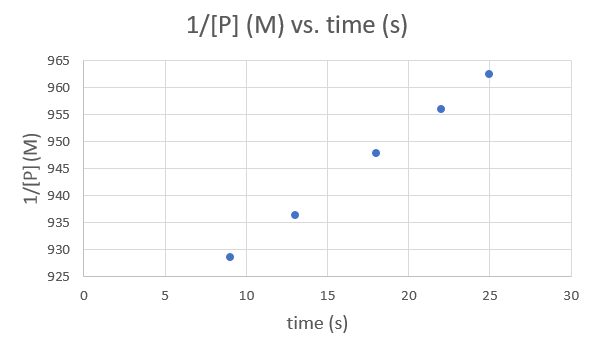.png)
Comme chaque graphique donne une ligne droite, l'ordre et la constante de vitesse de la réaction ne peuvent pas être déterminés.
Pour déterminer comment les concentrations changent en fonction du temps, il faut résoudre l'équation différentielle appropriée (c'est-à-dire la loi des taux différentiels).
La loi du taux d'ordre zéro prédit une décroissance linéaire de la concentration avec
le temps La loi du taux du premier ordre prédit une décroissance exponentielle de la concentration avec
le temps La loi du taux du deuxième ordre prédit une décroissance réciproque de la concentration avec le temps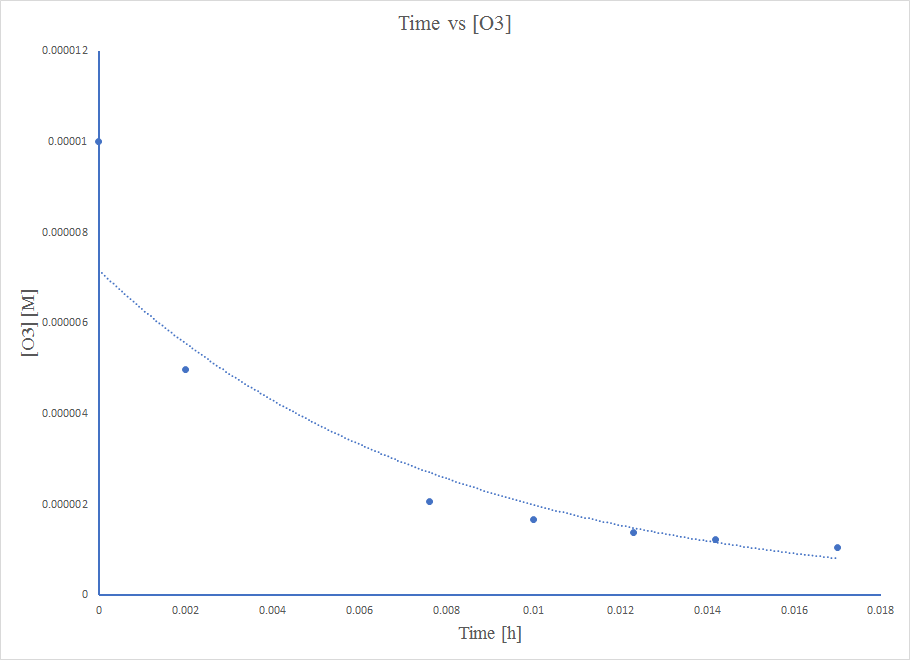
Le diagramme n'est pas linéaire, donc la réaction n'est pas d'ordre zéro.

Le diagramme n'est pas linéaire, de sorte que la réaction n'est pas de premier ordre.
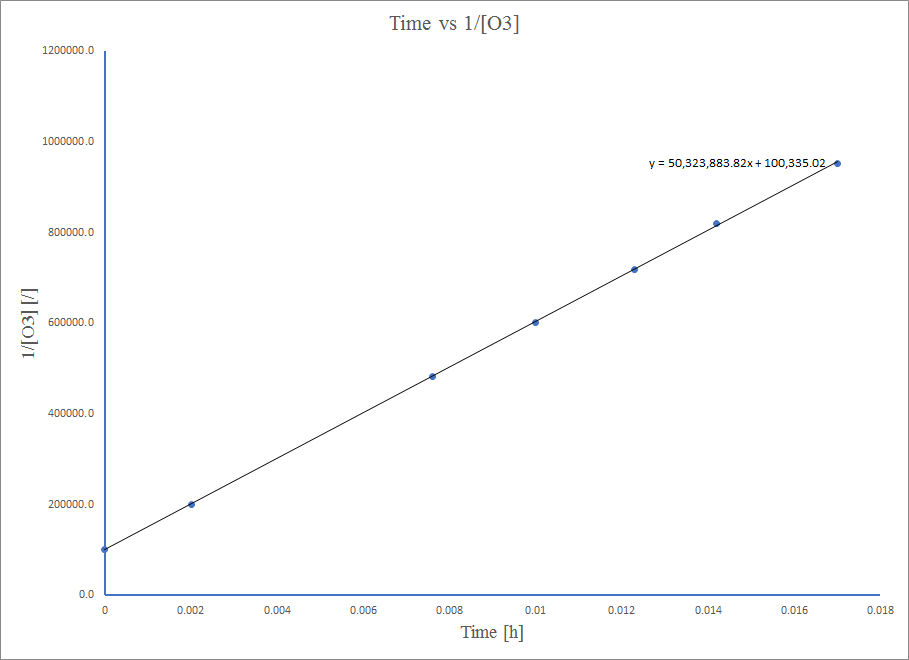
Le diagramme est bien linéaire, donc la réaction est de second ordre.
À une équation du second ordre,\( 1/[A] \ = k*t + 1/[A_0] \)
Ainsi, la valeur de K est la pente du graphe Time vs\( \frac{1}{\ce{O3}}\),
k = 50,3*10^6 L mol −1 h −1
- Réponse
-
Le diagramme est bien linéaire, donc la réaction est de second ordre.
k = 50,1 L mol −1 h −1
Q12.4.5
À partir des données fournies, utilisez une méthode graphique pour déterminer l'ordre et la constante de vitesse de la réaction suivante :
\[2X⟶Y+Z\]
| Heure (s) | 5,0 | 10,0 | 15,0 | 20,0 | 25,0 | 30,0 | 35,0 | 40,0 |
|---|---|---|---|---|---|---|---|---|
| [X] (M) | 0,0990 | 0,0497 | 0,0332 | 0,0249 | 0,0200 | 0,0166 | 0,0143 | 0,0125 |
- Solution
-
Afin de déterminer l'ordre de la réaction, nous devons tracer les données à l'aide de trois graphiques différents. Les trois graphes auront le temps en secondes comme axe des abscisses, mais c'est l'axe y qui sera différent. Un graphique représente la concentration en fonction du temps, le second représente le logarithme naturel de la concentration en fonction du temps et l'autre représente 1/concentration en fonction du temps. Quel que soit le graphique qui aboutit à une ligne, nous savons que ce doit être l'ordre de la réaction. Si nous obtenons une ligne en utilisant le premier graphique, elle sera d'ordre zéro, si c'est une droite pour le deuxième graphique, elle sera du premier ordre, et si c'est une ligne pour le troisième graphique, ce sera une réaction du second ordre. Tracons maintenant les données pour déterminer l'ordre.



Nous pouvons clairement voir que le troisième graphique, qui représente 1/M en fonction du temps, est une ligne droite tandis que les deux autres sont légèrement incurvés. Par conséquent, nous pouvons déterminer que la vitesse de cette réaction est de second ordre. Cela nous indique également que les unités de la constante de vitesse qui devraient être M -2 s -1 pour une réaction du second ordre.
Pour déterminer la constante de vitesse, appelée k, il suffit de déterminer la pente du troisième graphe puisque c'est l'ordre de cette réaction. Pour déterminer la pente de la droite, nous prenons deux points et soustrayons les valeurs y, puis nous les divisons par la différence des valeurs x. Voici comment procéder :
Utilisez les points (5, 10.101) et (40, 80).
Maintenant, utilisez-les pour obtenir le slop, c'est-à-dire la constante de vitesse : (80-10,101)/(40-5) = 1,997 = k
La constante de vitesse pour cette réaction du second ordre est donc de 1,997 M -1 s -1.
Q12.4.6
Quelle est la demi-vie de la désintégration du premier ordre du phosphore 32 ? \(\ce{(^{32}_{15}P⟶^{32}_{16}S + e- )}\)La constante de vitesse pour la décroissance est de 4,85 × 10 −2 jour −1.
- Solution
-
Il s'agit d'une réaction de premier ordre, nous pouvons donc utiliser notre équation de demi-vie ci-dessous :
\[t_{1/2}=\frac{0.693}{k}\nonumber \]
La constante de vitesse nous est donnée en unités par jour. Tout ce que nous avons à faire, c'est de l'intégrer à l'équation.
\[t_{1/2}=\frac{0.693}{4.85*10^{-2}}\nonumber \]
\[=14.3\; days\nonumber \]A12.4.6
14,3 d
Q12.4.7
Quelle est la demi-vie de la désintégration du premier ordre du carbone 14 ? \(\ce{(^6_{14}C⟶^7_{14}N + e- )}\)La constante de vitesse pour la décroissance est de 1,21 × 10 −4 an −1.
- Solution
-
Pour trouver la demi-vie, nous devons utiliser l'équation de demi-vie du premier ordre. Toutes les réactions de demi-vie subissent des réactions de premier ordre.
L'équation de demi-vie pour le premier ordre est\[t_{1/2}=ln2/k \nonumber \] où k est la constante de vitesse. La constante de vitesse pour le carbone 14 a été donnée sous la forme\(1.21 × 10^{-4} year^{−1}\).
Branchez-le dans l'équation. \[t_{1/2}=ln2/(1.21 × 10^{−4} year^{−1})\nonumber \]et résolvez pour\( t_{1/2}\).
Lorsque vous le calculez, la demi-vie du carbone 14 est de 5,73*10 3
- Réponse
-
La demi-vie du carbone 14 est calculée comme étant de 5,73*10 3
Q12.4.8
Quelle est la demi-vie de décomposition du NOCl lorsque la concentration de NOCl est de 0,15 M ? La constante de vitesse pour cette réaction du second ordre est de 8,0 × 10 −8 L/mol/s.
- Solution
-
La demi-vie d'une réaction, t 1/2, est le temps nécessaire pour que la concentration d'un réactif diminue de moitié par rapport à sa concentration initiale. Lorsque nous déterminons la demi-vie d'une réaction, nous devons d'abord prendre en compte l'ordre de réaction pour déterminer sa loi de vitesse. Dans ce cas, on nous dit que cette réaction est de second ordre, donc nous savons que la loi de taux intégrée est donnée comme suit :
\[\dfrac{1}{[A]} = kt + \dfrac{1}{[A]_0}\nonumber \]
En isolant le temps, nous constatons que :
\[t_{1/2} = \dfrac{1}{k[A]_0}\nonumber \]
Maintenant, il suffit de substituer les informations qui nous ont été données pour calculer\(t_{1/2}\), où la constante de vitesse est égale à 8,0 × 10 −8 L/mol/s et la concentration initiale,\({[A]_0}\), est égale à 0,15 M :\({k}\)
\[t_{1/2} = \dfrac{1}{(8.0×10^{-8})(0.15)} = {8.33×10^7 seconds}\nonumber \]
- Réponse
-
8,33 × 10 x 7 s
Q12.4.9
Quelle est la demi-vie de décomposition de l'O 3 lorsque la concentration de O 3 est de 2,35 × 10 −6 M ? La constante de vitesse pour cette réaction de second ordre est de 50,4 L/mol/h.
- Solution
-
Ajoutez des textes ici. Ne supprimez pas ce texte au préalable.
Comme la réaction est de second ordre, sa demi-vie est
\[t_{1/2}=\dfrac{1}{(50.4M^{-1}/h)[2.35×10^{-6}M]}\nonumber \]
Donc, la demi-vie est de 8443 heures.
Q12.4.10
La réaction du composé A pour donner les composés C et D s'est révélée être du second ordre dans A. La constante de vitesse de la réaction a été déterminée à 2,42 L/mol/s. Si la concentration initiale est de 0,500 mol/L, quelle est la valeur de t 1/2 ?
- Solution
-
Comme indiqué dans la question, la réaction du composé A entraînera la formation des composés C et D. Cette réaction s'est révélée être du second ordre dans A. Nous devrions donc utiliser l'équation du second ordre pour la demi-vie, qui relie la constante de vitesse et les concentrations initiales à la demi-vie :
\[t_{\frac{1}{2}}=\frac{1}{k[A]_{0}}\nonumber \]
Comme on nous a donné k (constante de vitesse) et la concentration initiale de A, nous avons tout ce qu'il faut pour calculer la demi-vie de A.
\[k=0.5\frac{\frac{L}{mol}}{s}\nonumber \]
\[[A]_{0}=2.42\frac{mol}{L}\nonumber \]
Lorsque nous branchons les informations données, remarquez que les unités s'annulent en quelques secondes.
\[t_{\frac{1}{2}}=\frac{1}{\frac{2.42Lmol^{-}}{s}[0.500\frac{mol}{L}]}=0.826 s\nonumber \]
- Réponse
-
0,826 s
Q12.4.11
La demi-vie d'une réaction du composé A donnant les composés D et E est de 8,50 minutes lorsque la concentration initiale de A est de 0,150 mol/L. Combien de temps faudra-t-il pour que la concentration tombe à 0,0300 mol/L si la réaction est (a) du premier ordre par rapport à A ou (b) un second ordre par rapport à A ?
- Solution
-
Organisez les variables données :
(demi-vie de A)\(t_{1/2}=8.50min\)
(concentration initiale de A)\([A]_{0}=0.150mol/L\)
(concentration cible de A)\([A]=0.0300mol/L\)Déterminez la constante de vitesse k en utilisant les formules de demi-vie pour chaque ordre respectif. Après avoir trouvé k, utilisez la loi de vitesse intégrée correspondant à chaque ordre et aux concentrations initiale et cible de A pour déterminer le temps qu'il a fallu pour que la concentration baisse.
a) premier ordre en ce qui concerne A
(demi-vie)\(t_{1/2}=\frac{ln(2)}{k}=\frac{0.693}{k}\)
(réarrangée pour k)\(k=\frac{0.693}{t_{1/2}}\)
(branchez t 1/2 = 8,50 min)\(k=\frac{0.693}{8.50min}=0.0815min^{-1}\)(loi de taux intégrée)\(ln[A]=-kt+ln[A]_{0}\)
(réarrangée pour t)\(ln(\frac{[A]}{[A]_{0}})=-kt\)
\(-ln(\frac{[A]}{[A]_{0}})=kt\)
\(ln(\frac{[A]}{[A]_{0}})^{-1}=kt\)
\(ln(\frac{[A]_{0}}{[A]})=kt\)
\(t=\frac{ln(\frac{[A]_{0}}{[A]})}{k}\)
(variables de branchement)\(t=\frac{ln(\frac{0.150mol/L}{0.0300mol/L})}{0.0815min^{-1}}=\frac{ln(5.00)}{0.0815min^{-1}}=19.7min\)(b) deuxième ordre en ce qui concerne A
(demi-vie)\(t_{1/2}=\frac{1}{k[A]_{0}}\)
(réarrangé pour k)\(k=\frac{1}{t_{1/2}[A]_{0}}\)
(variables de branchement)\(k=\frac{1}{(8.50min)(0.150mol/L)}=\frac{1}{1.275min\cdot mol/L}=0.784L/mol\cdot min\)(loi de taux intégrée)\(\frac{1}{[A]}=kt+\frac{1}{[A]_{0}}\)
(réarrangée pour t)\(\frac{1}{[A]}-\frac{1}{[A]_{0}}=kt\)
\(t=\frac{1}{k}(\frac{1}{[A]}-\frac{1}{[A]_{0}})\)
(variables de branchement)\(t=\frac{1}{0.784L/mol\cdot min}(\frac{1}{0.0300mol/L}-\frac{1}{0.150mol/L})=\frac{1}{0.784L/mol\cdot min}(\frac{80}{3}L/mol)=34.0min\)
- Réponse
-
a) 19,7 minutes
b) 34,0 minutes
Q12.4.12
Certaines bactéries sont résistantes à l'antibiotique pénicilline car elles produisent de la pénicillinase, une enzyme d'un poids moléculaire de 3 × 10 4 g/mol qui convertit la pénicilline en molécules inactives. Bien que la cinétique des réactions catalysées par des enzymes puisse être complexe, à de faibles concentrations, cette réaction peut être décrite par une équation de vitesse qui est du premier ordre dans le catalyseur (pénicillinase) et qui implique également la concentration de pénicilline. À partir des données suivantes : 1,0 L d'une solution contenant 0,15 µg (0,15 × 10 −6 g) de pénicillinase, déterminer l'ordre de la réaction par rapport à la pénicilline et la valeur de la constante de vitesse.
| [Pénicilline] (M) | Débit (mol/L/min) |
|---|---|
| 2,0 × 10 −6 | 1,0 × 10 −10 |
| 3,0 × 10 −6 | 1,5 × 10 −10 |
| 4,0 × 10 −6 | 2,0 × 10 −10 |
- Solution
-
La première étape consiste à résoudre l'ordre ou la réaction. Cela peut être fait en établissant deux expressions qui assimilent le débit à la constante de vitesse multipliée par la concentration molaire de pénicilline élevée à la puissance de son ordre. Une fois les deux expressions configurées, nous pouvons les diviser pour annuler k (constante de taux) et utiliser un logarithme de base pour résoudre l'exposant, qui est l'ordre. Cela ressemblera à ceci.
débit (mol/L/min) =k [M] x
(1,0 x 10 -10) =k [2,0 x 10 -6] x
(1,5 x 10 -10) =k [3,0 x 10-6] x
En divisant les deux équations, on obtient l'expression :
(2/3) = (2/3) x
*Une seule équation de ratio peut également être configurée pour résoudre l'ordre de réaction :
*\[\frac{rate_{1}}{rate_{2}}=\frac{k[Penicillin]_{1}^{x}}{k[Penicillin]_{2}^{x}}\nonumber \]
*Nous résolvons ensuite x de la même manière.
*\[\frac{1.0x10^{-10}}{1.5x10^{-10}}=\frac{[2.0x10^{-6}]^{x}}{[3.0x10^{-6}]^{x}}\nonumber \]
Nous pouvons maintenant utiliser le logarithme naturel pour résoudre x, ou simplement et intuitivement voir que pour que l'équation fonctionne, x doit être égal à un. La réaction est donc du premier ordre.
Maintenant que nous avons l'ordre de la réaction, nous pouvons procéder à la résolution de la valeur de la constante de vitesse. En substituant x=1 dans notre première équation, on obtient l'expression suivante :(1 x 10 -10) =k [2,0 x 10 -6] 1
k= (1 x 10 -10)/(2 x 10 -6)
k= (5 x 10 -5) min-1
Nous avons une unité de min -1 parce que nous avons divisé (mol/L/min) par molarité, qui est en (mol/L), ce qui donne une unité de min -1.
Nous avons reçu deux informations importantes pour régler le problème. Il est indiqué que l'enzyme a un poids moléculaire de 3 × 10 4 g/mol et que nous avons une solution d'un litre contenant (0,15 x 10 -6 g) de pénicillinase. En divisant la quantité de grammes par le poids moléculaire, on obtient 5 x 10 -12 moles.
(0,15 x 10 -6) g/ (3 x 10 4) g/mol = (5 x 10 -12) mol
Maintenant que nous avons le nombre de moles, nous pouvons diviser notre constante de vitesse par cette valeur.
(5 x 10 -5) min -1/(5 x 10 -12) mol = (1 x 10 7) mol -1 min -1 min -1
Réponse
-
La réaction est du premier ordre avec k = 1,0 × 10 7 mol −1 min −1
Q12.4.13
Le technétium-99 et le thallium-201 sont tous deux utilisés pour imager le muscle cardiaque chez les patients soupçonnés d'avoir des problèmes cardiaques. Les demi-vies sont respectivement de 6 h et 73 h. Quel pourcentage de radioactivité resterait pour chacun des isotopes après 2 jours (48 h) ?
- Solution
-
Ce problème nous demande quel est le pourcentage de radioactivité restant après un certain temps pour les deux isotopes après 48 heures. Nous devons identifier une équation qui nous aidera à résoudre ce problème et nous pouvons déterminer que nous pouvons déterminer ces informations à l'aide de l'équation du premier ordre.
Cette équation Ln (N/N o) = -kt indique que le logarithme naturel de la fraction restante est égal à la constante de vitesse multipliée par le temps. Pour déterminer la constante de vitesse, nous pouvons également calculer ,693 sur la demi-vie indiquée dans les informations.
Pour le Technétium-99, nous pouvons déterminer la constante de vitesse en utilisant la deuxième équation : 0,693/6 heures = 0,1155 h -1
Maintenant que nous avons la constante de vitesse, nous pouvons l'intégrer : Ln (N/N o) =- (0,155h -1) (48h) donc Ln (N/N o) =-5,544 et si nous prenons l'inverse du logarithme naturel, nous obtenons (N/N o) =3,9x10 -3 et si nous multiplions cela par 100, nous obtenons 0,39 % restant.
Nous pouvons faire le même processus pour Thallium-201 et le plugin : 0,693/73 heures = 0,009493151 h -1 et lorsque nous insérons cela dans l'équation du premier ordre, nous obtenons :
Ln (N/N o) =- (0,009493h -1) (48h) donc Ln (N/N o) =-0,45567248 et lorsque nous prenons l'inverse du logarithme naturel, nous obtenons (N/N o) = 0,6340 % et lorsqu'il est multiplié par 100, nous obtenons 63,40 % restant, ce qui est logique puisque sa demi-vie est de 73 heures et que seulement 48 heures se sont écoulées, la moitié de la quantité n'a pas encore été consommée.
- Réponse
-
Technétium 99 : 0,39 %
Thallium-201 : 63,40 %
Q12.4.14
Il existe deux molécules de formule C 3 H 6. Le propène est\(\ce{CH_3CH=CH_2}\) le monomère du polymère polypropylène, utilisé pour les tapis intérieurs/extérieurs. Le cyclopropane est utilisé comme anesthésique :

Lorsqu'il est chauffé à 499 °C, le cyclopropane se réorganise (s'isomérise) et forme du propène avec une constante de vitesse de 5,95 × 10 −4 s −1. Quelle est la demi-vie de cette réaction ? Quelle fraction du cyclopropane reste après 0,75 h à 499 °C ?
- Solution
-
Utilisez l'équation\[ t{_1}{_/}{_2} = \frac{ln2} k\nonumber \] puisqu'il s'agit d'une réaction de premier ordre. Vous pouvez voir qu'il s'agit d'une réaction de premier ordre en raison des unités de mesure de la constante de vitesse, qui est s -1. Différents ordres de réactions conduisent à des constantes de vitesse différentes, et une constante de vitesse de s -1 sera toujours du premier ordre.
Branchez l'équation et vous obtenez une demi-vie = 1164,95 secondes. Pour convertir cela en heures, nous diviserions ce nombre par 3600 secondes/heure, pour obtenir 0,324 heure.
Utilisez la loi de taux du premier ordre intégrée\[ln\frac{[A]}{[A]_0} = -kt\nonumber \]. Dans cette équation, [A] 0 représente la quantité initiale de composé présent au temps 0, tandis que [A] représente la quantité de composé restant après la réaction. Par conséquent, la fraction\[\frac{[A]}{[A]_0}\nonumber \] est égale à la fraction de cyclopropane qui reste après un certain temps, dans ce cas, 0,75 heure.
Substituez x à la fraction de\[\frac{[A]}{[A]_0}\nonumber \] dans la loi de taux intégrée :\[ln\frac{[A]}{[A]_0} = -kt\nonumber \]\[ln(x) = -5.95x10^{-4}(0.75)\nonumber \]\[x=e^{(-0.000595)(0.75)}\nonumber \] = 0,20058 = 20 %.
La demi-vie est donc de 0,324 heure et 20 % du cyclopropane restera, 80 % ayant formé du propène.
- Réponse
-
0,324 heures ; il reste 20 %
Q12.4.16
Le fluor 18 est un isotope radioactif qui se désintègre par émission de positrons pour former de l'oxygène 18 avec une demi-vie de 109,7 min. (Un positron est une particule ayant la masse d'un électron et une seule unité de charge positive ; l'équation nucléaire l'est\(\ce{^{18}_9F ⟶ _8^{18}O + ^0_{1}e^+}\).) Les médecins utilisent le 18 F pour étudier le cerveau en injectant une quantité de glucose fluoro-substitué dans le sang d'un patient. Le glucose s'accumule dans les régions où le cerveau est actif et a besoin d'être nourri.
- Quelle est la constante de vitesse pour la décomposition du fluor 18 ?
- Si un échantillon de glucose contenant du fluor radioactif 18 est injecté dans le sang, quel pourcentage de radioactivité restera-t-il après 5,59 h ?
- Combien de temps faut-il au Fe pour que 99,99 % des 18 F se désintègrent ?
- Solution
-
a) La désintégration nucléaire d'un isotope d'un élément est représentée par l'équation du premier ordre :
ln (N/N0) = −kt
Où t est le temps, N0 est la quantité initiale de la substance, N est la quantité de substance après le temps t et k est la constante de vitesse. Nous pouvons réarranger l'équation et isoler k afin de pouvoir résoudre la constante de vitesse :
k = [-ln (N/N0)]/t
On nous indique que le fluor 18 a une demi-vie de 109,7 minutes. Puisque nous avons la demi-vie, nous pouvons choisir une valeur arbitraire pour N 0 et utiliser la moitié de cette valeur pour N. Dans ce cas, nous choisissons 100 pour N 0 et 50 pour N. Nous pouvons maintenant intégrer ces valeurs dans l'équation ci-dessus et résoudre pour k.
k = [-ln (50/100)]/109,7
k = 0,6931/109,7 = 0,006319 min-1
La constante de vitesse de cette réaction est de 0,006319 min-1.
b) Pour ce problème, nous pouvons utiliser la même équation de la partie a :
ln (N/N0) = −kt
Cependant, cette fois, on nous indique le temps écoulé au lieu de la demi-vie, et on nous demande de déterminer le pourcentage de radioactivité du fluor 18 restant après cette période. Dans ce problème, nous devons intégrer les valeurs de N0, k (déterminé à partir de la partie a) et t.
Mais d'abord, comme on nous donne le temps écoulé en heures, nous devons le convertir en minutes :
5,59 heures x (60 minutes/1 heure) = 335,4 minutes
Cela nous donne la valeur de t. Nous avons également des valeurs pour k (0,006319 min -1) et N 0 (encore une fois un nombre arbitraire). Nous pouvons maintenant intégrer des valeurs dans l'équation d'origine, ce qui nous donne :
ln (N/100) = − (0,006319) (335,4)
Nous résolvons cette équation en prenant l'exponentielle des deux côtés :
e ln (N/100) = e − (0,006319) (335,4)
où e ln est égal à 1 et maintenant on peut juste résoudre pour N :
N/100 = e − (0,006319) (335,4)
N = [e − (0,006319) (335,4)] x 100 = 12,0
Comme 100 a été utilisé comme quantité initiale et que 12,0 a été déterminé comme quantité restante, 12,0 peut être utilisé comme pourcentage de la quantité restante de radioactivité de fluor 18. Ainsi, le pourcentage de radioactivité du fluor 18 restant après 5,59 heures est de 12,0 %.
c) Cette partie de la question ressemble beaucoup aux deux parties précédentes, mais cette fois, on nous donne la quantité initiale de radioactivité, la quantité finale de radioactivité et on nous demande de déterminer le temps qu'il a fallu pour que cette quantité de radioactivité se désintègre. Nous pouvons utiliser la même équation :
ln (N/N0) = −kt
Cependant, on nous donne maintenant N et N 0 et nous avons déjà déterminé k d'avant. On nous dit que 99,99 % de la radioactivité s'est dégradée, de sorte que nous pouvons utiliser 100 et 0,01 pour N 0 et N respectivement. Nous intégrons ces valeurs à l'équation, résolvons t et obtenons
ln (0,01/1000) = −0,006319 t
-9,21 = −0,006319 t
t = 1458 minutes
Il faut donc 1 458 minutes pour que 99,99 % de la radioactivité se désintègre.
- Réponse
-
a) 0,006319 min-1
b) 12,0 %
c) 1458 minutes
Q12.4.17
Supposons que la demi-vie des stéroïdes pris par un athlète soit de 42 jours. En supposant que les stéroïdes se biodégradent par un processus de premier ordre, combien\(\dfrac{1}{64}\) de temps faudrait-il pour que la dose initiale reste dans le corps de l'athlète ?
- Solution
-
252 jours
pour une réaction du premier ordre : t 1/2 = 0,693/k
k = 0,693/42
k = 0,0165
pour la réaction du premier ordre : [A] = [A] 0 e -kt
1/64 initial signifie que : [A] = 1/64 [A] 0
donc : 1/64 [A] 0 = [A] 0 e -0,0165t
t = 252 jours
Q12.4.18
Récemment, le squelette du roi Richard III a été découvert sous un parking en Angleterre. Si les échantillons de tissus prélevés dans le squelette contiennent environ 93,79 % du carbone 14 attendu dans les tissus vivants, en quelle année le roi Richard III est-il mort ? La demi-vie du carbone 14 est de 5 730 ans.
- Solution
-
Pour savoir en quelle année le roi Richard III est mort, définissez [A]/[A 0] (le pourcentage de carbone 14 encore contenu) à 0,5 fois (t) /demi-vie (t 1/2) ou utilisez l'équation N (t) = N 0 e -rt.
À l'aide de la première équation :
\(A/A_{0}\)=\(0.5^{t/t_{1/2}}\) insérez les nombres donnés\(.9379 = 0.5^{t/5730}\) et résolvez pour t.
\(ln.9379\)=\((t/5730)(ln0.5)\) (en utilisant la règle des journaux)
\(-.0641\)=\((t/5730)(-.693)\)
\(-367.36\)=\(-.693t\)
\(t = 530.1 years\)
L'utilisation de\(N(t) = N_{0}e^{-rt}\) ce problème est résolue comme suit :
\(1/2 = e^{-5730r}\)
\(r = 0.000121\)
Maintenant que nous savons ce qu'est r, nous pouvons utiliser cette valeur dans notre formule initiale et résoudre pour t, le nombre d'années qui se sont écoulées.
Cette fois, nous utilisons 93,78, le pourcentage du carbone 14 restant sous forme de N (t) et 100 comme original, N 0.
\(93.78 = 100e^{-0.000121t}\)
\(t = 530.7\)ans
Une autre façon de le faire est d'utiliser ces deux équations :
λ =\(\dfrac{0.693}{t_{1/2}}\) et\(\dfrac{n_{t}}{n_{0}}\) = -λt
\(n_{t}\)= concentration au temps t (93,79)
\(n_{0}\)= concentration initiale (100)
Déterminez d'abord le lambda ou la constante de désintégration en ajoutant la demi-vie.
Ajoutez ensuite lambda et les autres nombres dans la deuxième équation, et résolvez pour t- qui devrait également être égal à 530,1 ans.
Si nous voulons savoir en quelle année le roi Richard III est mort, nous prenons l'année en cours, 2017, et soustrayons 530 ans. Ce faisant, nous découvrons que le roi Richard III est mort en 1487.
- Réponse
-
Le roi Richard III est décédé en 1487
Q12.4.19
La nitroglycérine est un explosif extrêmement sensible. Au cours d'une série d'expériences soigneusement contrôlées, des échantillons de l'explosif ont été chauffés à 160 °C et leur décomposition du premier ordre a été étudiée. Déterminez les constantes de vitesse moyennes pour chaque expérience à l'aide des données suivantes :
| Initiale [C 3 H 5 N 3 O 9] (M) | 4,88 | 3,52 | 2,29 | 1,81 | 5,33 | 4,05 | 2,95 | 1,72 |
|---|---|---|---|---|---|---|---|---|
| t (s) | 300 | 300 | 300 | 300 | 180 | 180 | 180 | 180 |
| % Décomposé | 52,0 | 52,9 | 53,2 | 53,9 | 34,6 | 35,9 | 36,0 | 35,4 |
- Solution
-
Nous devons d'abord comprendre ce que demande la question : la constante de taux moyenne. La constante de vitesse moyenne est la variable « k » lorsqu'on parle de cinétique et elle peut être définie comme la constante de proportionnalité dans l'équation qui exprime la relation entre la vitesse d'une réaction chimique et les concentrations des substances réactives. Sachant que nous devons trouver K dans cette réaction du premier ordre, nous pouvons utiliser des formules qui incluent « k », les concentrations\([A]_o and [A]_t\) initiale et finale et la demi-vie « t ». Comme il s'agit d'une réaction de premier ordre, nous pouvons examiner les équations du premier ordre, et ce faisant, nous en trouvons une qui inclut les variables données dans la question :\[\ln[A]_t=-kt+\ln[A]_o\nonumber \]
Pour la première réaction, nous avons une concentration initiale de 4,88 M et un pourcentage de décomposition. Pour déterminer la concentration finale, il faut multiplier la concentration initiale par le pourcentage décomposé pour connaître la quantité décomposée, et la soustraire de l'original pour connaître la quantité restante : 4,88 M x 0,52 = 2,54 M et 4,88 M-2,54 M = 2,34 M
Maintenant, nous avons les variables dont nous avons besoin, et nous les intégrons à l'équation ci-dessus :
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.34M]=-k(300s)+\ln[4.88M]\)
k=\({-(\ln[2.34M]-\ln[4.88M])}\over 300\)
\(k=2.45x10^{-3}\)
Comme il demande la constante de vitesse de chaque expérience, nous devons maintenant suivre la même procédure pour chaque ensemble de données afin de trouver la constante de vitesse :
Deuxième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.66M]=-k(300s)+\ln[3.52M]\)
k=\({-(\ln[1.66M]-\ln[3.52M])}\over 300\)
\(k=2.51x10^{-3}\)
Troisième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.07M]=-k(300s)+\ln[2.29M]\)
k=\({-(\ln[1.07M]-\ln[2.29M])}\over 300\)
\(k=2.54x10^{-3}\)
Quatrième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[0.834M]=-k(300s)+\ln[1.81M]\)
k=\({-(\ln[0.834M]-\ln[1.81M])}\over 300\)
\(k=2.58x10^{-3}\)
Cinquième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[3.49M]=-k(180s)+\ln[5.33M]\)
k=\({-(\ln[3.49M]-\ln[5.33M])}\over 180\)
\(k=2.35x10^{-3}\)
Sixième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.60M]=-k(180s)+\ln[4.05M]\)
k=\({-(\ln[2.60M]-\ln[4.05M])}\over 180\)
\(k=2.46x10^{-3}\)
Septième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.89M]=-k(180s)+\ln[2.95M]\)
k=\({-(\ln[1.89M]-\ln[2.95M])}\over 180\)
\(k=2.47x10^{-3}\)
Huitième expérience
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.11M]=-k(180s)+\ln[1.72M]\)
k=\({-(\ln[1.11M]-\ln[1.72M])}\over 180\)
\(k=2.43x10^{-3}\)
- Réponse
-
[A] 0 (M) k × 10 (3 x −1) 4,88 2,45 3,52 2,51 2,29 2,54 1,81 2,58 5,33 2,35 4,05 2,44 2,95 2,47 1,72 2,43
Q12.4.20
Au cours des 10 dernières années, le 1,3-butadiène, un hydrocarbure insaturé,\(\ce{(CH2=CH–CH=CH2)}\) s'est classé 38e parmi les 50 principaux produits chimiques industriels. Il est principalement utilisé pour la fabrication de caoutchouc synthétique. Un isomère existe également sous forme de cyclobutène :

L'isomérisation du cyclobutène en butadiène est du premier ordre et la constante de vitesse a été mesurée à 2,0 × 10 −4 s −1 à 150 °C dans un flacon de 0,53 L. Déterminer la pression partielle du cyclobutène et sa concentration après 30 minutes si une réaction d'isomérisation est réalisée à 150 °C avec une pression initiale de 55 torr.
- Solution
-
Comme il s'agit d'une réaction de premier ordre, la loi de vitesse intégrée est la suivante : Pression\([A_{t}]=[A_{0}]e^{-kt}\)
partielle : Utilisez la loi de vitesse intégrée pour trouver la pression partielle à 30 minutes :Utilisez\(A_0\) = 55 torr, t = 30 min et k =\(2.0 * 10^{-4}s^{-1}\) pour résoudre l'équation de la loi de vitesse intégrée :
\([A_{30}]=(55 torr)*e^{-(2.0x10^{-4}\frac{1}{sec})(30min\cdot\frac{60sec}{1 min})}\)
Résolvez cette équation pour obtenir :
\([A_{30}]=(55 torr)*e^{-0.36}\)
\(A_{30}]\)= 38,37 torr.
Concentration initiale : Déterminez la concentration initiale en utilisant la loi des gaz idéaux.
La loi idéale sur les gaz est donnée par\(PV = nRT → n = \frac{PV}{RT}\). Utilisez cette forme de la loi des gaz pour résoudre la concentration initiale n.
Utilisez V = 0,53 L, R = 0,08206\(\frac{L*atm}{mol*L}\), T = 423,15 K et P\(\frac{1 atm}{760}\) = 0,07237 atm.
Résolvez l'équation du gaz idéal en utilisant les valeurs suivantes :
\(n=\frac{(55torr)(0.53L)}{(0.08206\frac{L*atm}{mol*K})(423.15K)} = 0.00110\)moles de cyclobutène.
Déterminez maintenant la concentration initiale de cyclobutène à\(A_0\) l'aide de l'équation\([A_0] = \frac{n}{V}\) :
\(A_0 = \frac{n}{V} = \frac{0.00110 moles}{0.53 L} = 0.00208 M\)
Concentration à 30 minutes : Déterminez la concentration de cyclobutène à 30 minutes en utilisant la loi de vitesse intégrée donnée ci-dessus, en utilisant le temps t = 30 minutes ou 1800 secondes.
\([A_{30}]=(0.00208M)e^{-0.36}= 0.00145M\)
Ainsi, après 30 minutes, la concentration en cyclobutène est de 0,00145 M et la pression partielle de 38,37 torr.
- Réponse
-
Pression partielle : 38,37 torr.
Concentration : 0,00145 M
12.5 : Théorie des collisions
Q12.5.1
Des réactions chimiques se produisent lorsque des réactifs entrent en collision. Quels sont les deux facteurs qui peuvent empêcher qu'une collision ne produise une réaction chimique ?
- Solution
-
Les deux facteurs qui peuvent empêcher qu'une collision ne produise une réaction chimique sont les suivants :
1. Énergie cinétique de la molécule
Pour que des réactions chimiques se produisent, les molécules ont besoin d'une vitesse suffisante pour surmonter l'énergie d'activation minimale nécessaire pour rompre les anciennes liaisons et former de nouvelles liaisons avec d'autres molécules. À des températures plus élevées, les molécules possèdent la quantité minimale d'énergie cinétique nécessaire, ce qui garantit que les collisions seront suffisamment énergétiques pour provoquer une réaction.
2. L'orientation des molécules lors de la collision
Deux molécules doivent entrer en collision dans la bonne orientation pour que la réaction se produise. Les molécules doivent s'orienter correctement pour qu'une autre molécule entre en collision au bon état d'activation.
Q12.5.2
Lorsque chaque collision entre des réactifs entraîne une réaction, qu'est-ce qui détermine la vitesse à laquelle la réaction se produit ?
- Solution
-
Il doit y avoir un contact entre les réactifs pour qu'une réaction se produise. Plus les réactifs entrent en collision, plus les réactions peuvent survenir. Les facteurs qui déterminent les vitesses de réaction incluent la concentration des réactifs, la température, l'état physique des réactifs, la surface et l'utilisation d'un catalyseur. La vitesse de réaction augmente généralement à mesure que la concentration d'un réactif augmente. L'augmentation de la température augmente l'énergie cinétique moyenne des molécules, ce qui les fait entrer en collision plus fréquemment, ce qui augmente la vitesse de réaction. Lorsque deux réactifs se trouvent dans la même phase fluide, leurs particules entrent en collision plus fréquemment, ce qui augmente la vitesse de réaction. Si la surface d'un réactif augmente, davantage de particules sont exposées à l'autre réactif, donc davantage de collisions se produisent et la vitesse de réaction augmente. Un catalyseur participe à une réaction chimique et augmente la vitesse de réaction sans se modifier.
Q12.5.3
Quelle est l'énergie d'activation d'une réaction et comment cette énergie est-elle liée au complexe activé de la réaction ?
- Solution
-

L'énergie d'activation est la barrière énergétique qui doit être surmontée pour qu'une réaction se produise. Pour que les molécules atteignent un état qui leur permet de se rompre et de former des liaisons, les molécules doivent être contorsionnées (déformées ou courbées) dans un état instable appelé état de transition. L'état de transition est un état à haute énergie, et une certaine quantité d'énergie, l'énergie d'activation, doit être ajoutée pour que la molécule l'atteigne. Comme l'état de transition est instable, les molécules du réactif n'y restent pas longtemps, mais passent rapidement à l'étape suivante de la réaction chimique. Le complexe activé est l'énergie la plus élevée de l'état de transition de la réaction.
Q12.5.5
Décrire comment des méthodes graphiques peuvent être utilisées pour déterminer l'énergie d'activation d'une réaction à partir d'une série de données incluant la vitesse de réaction à différentes températures.
- Solution
-
Cette méthode est basée sur l'équation d'Arrhenius qui peut être utilisée pour montrer l'effet d'un changement de température sur la constante de vitesse, et donc sur la vitesse de réaction.
La constante de vitesse est différente de la vitesse de réaction en ce sens que la vitesse de réaction est la mesure de la rapidité ou de la lenteur d'une réaction chimique, tandis qu'une constante de vitesse est une constante qui montre la relation entre la vitesse de réaction et les concentrations des réactifs ou des produits.
Par exemple, pour la réaction\(A + B \rightarrow C\), the rate law would be:
\(rate = k[A]^a[B]^b\)
k = constante de vitesse
[A] = concentration du réactif A
a = ordre de réaction par rapport à A
[B] = concentration du réactif B
b = ordre de réaction par rapport à B
Toutefois, la constante de vitesse reste constante uniquement si vous modifiez la concentration des réactifs. Si vous modifiez la température ou le catalyseur de la réaction, la constante de vitesse changera, comme le montre l'équation d'Arrhenius :
\(k = Ae^\frac{-E_a}{RT}\)
\(ln \left(\frac{k_1}{k_2}\right) = \left(\frac{-E_a}{R}\right)\left(\frac{1}{T_1} - \frac{1}{T_2}\right)\)
k = constante de vitesse
A = facteur de fréquence
\(E_a\) = activation energy
e = fonction exponentielle,\(e^x\)
R = constante de gaz
T = température (K)

En d'autres termes, l'énergie d'activation d'une réaction,\(E_a\), from a series of data that includes the rate of reaction, k, at varying temperatures can be determined by graphing it on a plot of \(\ln k\) versus \(\frac{1}{T}\). You can then use the slope of the graph you have plotted to solve for \(E_a\) by setting the slope equal to \(\frac{-E_a}{R}\).
Q12.5.6
How does an increase in temperature affect rate of reaction? Explain this effect in terms of the collision theory of the reaction rate.
S12.5.6
Collision theory states that the rates of chemical reactions depend on the fraction of molecules with the correct orientation, fraction of collisions with required energy, and the collision frequency. Because the fraction of collisions with required energy is a function of temperature, as temperature increases, the fraction of collisions with required energy also increases. The kinetic energy of reactants also increases with temperature which means molecules will collide more often increasing collisions frequency. With increased fraction of collisions with required energy and collisions frequency, the rate of chemical reaction increases. We see mathematically, from the Arrhenius equation, that temperature and the rate constant are related.
\[k=Ae^{\frac {E_a}{RT}}\]
where k is the rate constant, A is a specific constant, R is 8.3145 J/K, Ea is the reaction-specific activation energy in J, and T is temperature in K. We see from the equation that k is very sensitive to changes in the temperature.
Q12.5.7
The rate of a certain reaction doubles for every 10 °C rise in temperature.
- How much faster does the reaction proceed at 45 °C than at 25 °C?
- How much faster does the reaction proceed at 95 °C than at 25 °C?
- Solution
-
By finding the difference in temperature, 45 °C - 25 °C, we get 20 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the rate of the reaction experienced a 20 °C increase in temperature, we see that the reaction rate doubled twice (22 = 4). As a result, the reaction proceeds four times faster.
Following the same process as in part a, we get the difference in temperature to be 70 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the system experienced a 70 °C change, we see that the reaction doubled seven times (27 = 128). We can see the reaction proceeds 128 times faster.
(a) 4-times faster (b) 128-times faster
Q12.5.8
In an experiment, a sample of NaClO3 was 90% decomposed in 48 min. Approximately how long would this decomposition have taken if the sample had been heated 20 °C higher?
S12.5.8
First off, it is important to recognize that this decomposition reaction is a first-order reaction, which can be written as follows: \(\mathrm2NaClO_3\to2NaCl + 3O_2\)
Understanding this, it is important to be able to then be able to recognize which equation would be most useful given the initial conditions presented by the question. Since we are dealing with time, percentage of material left, and temperature, the only viable equation that could relate all of this would be the Arrhenius Equation, which is written as follows: \(\mathrm \ln(\frac{k_2}{k_1}) = \frac {Ea}{R}({\frac1{t_1}}-{\frac{1}{t_{2}}})\)
However, this problem does not give us enough information such as what the activation energy is or the initial temperature in order to mathematically solve this problem. Additionally, the problem tells us to approximate how long the decomposition would take, which means we are asked to answer this question conceptually based on our knowledge of thermodynamics and reaction rates. As a general rule of thumb, we know that for every 10˚C rise in temperature the rate of reaction doubles. Since the question tells us that there is a 20˚C rise in temperature we can deduce that the reaction rate doubles twice, as per the general rule mentioned before. This means the overall reaction rate for this decomposition would quadruple, or would be 4 times faster than the reaction rate at the initial temperature.
We can gut check this answer by recalling how an increase in the average kinetic energy (temperature) decreases the time it takes for the reaction to take place and increase the reaction rate. Thus, if we increase the temperature we should have a faster reaction rate.
Q12.5.9
The rate constant at 325 °C for the decomposition reaction \(\ce{C4H8⟶2C2H4}\) is 6.1 × 10−8 s−1, and the activation energy is 261 kJ per mole of C4H8. Determine the frequency factor for the reaction.
- Solution
-
S12.5.9
Using the Arrhenius equation allows me to find the frequency factor, A.
k=Ae-Ea/RT
k, Ea, R, and T are all known values. k, Ea, and T are given in the problem as 6.1x10-8, 261 kJ, and 598 K, respectively.
So, plugging them into the equation gives:
6.1x10-8 s-1=Ae(-261000 J)/(8.3145 J/mol)(598 K)
Take e(-261000 J)/(8.3145 J/mol)(598) and get 1.59 x 10-23. Divide k, 6.1 x 10-8, by 1.59 x 10-23 and get A=3.9 x 1015s-1
-
A12.5.9
\(\mathrm{3.9×10^{15}\:s^{−1}}\)
Q12.5.10
The rate constant for the decomposition of acetaldehyde (CH3CHO), to methane (CH4), and carbon monoxide (CO), in the gas phase is 1.1 × 10−2 L/mol/s at 703 K and 4.95 L/mol/s at 865 K. Determine the activation energy for this decomposition.
S12.5.10
The equation for relating the rate constant and activation energy of a reaction is the Arrhenius equation:
\[k = Ae^ {-\frac{E_a}{RT}}\]
When given two rate constants at two different temperatures but for the same reaction, the Arrhenius equation can be rewritten as:
\[ln (\frac{k_2}{k_1}) = \frac{E_a}{R} (\frac{1}{T_1} - \frac{1}{T_2})\]
In this problem, all the variables are given except for the Ea (activation energy).
k1 = 1.1 × 10−2 L/mol/s
T1 = 703 K
k2 = 4.95 L/mol/s
T2 = 865 K
R = 8.314 J/(mol K) (Ideal Gas Constant)
Now plug in all these values into the equation, and solve for Ea.
\[ln (\frac{4.95\frac{L}{mol×s}}{1.1 × 10^{-2}\frac{L}{mol×s}}) = \frac{E_a}{8.314 × 10^{-3}\frac{kJ}{mol×K}} (\frac{1}{703} - \frac{1}{865})\]
Ea = 190 kJ (2 sig figs)
Q12.5.11
An elevated level of the enzyme alkaline phosphatase (ALP) in the serum is an indication of possible liver or bone disorder. The level of serum ALP is so low that it is very difficult to measure directly. However, ALP catalyzes a number of reactions, and its relative concentration can be determined by measuring the rate of one of these reactions under controlled conditions. One such reaction is the conversion of p-nitrophenyl phosphate (PNPP) to p-nitrophenoxide ion (PNP) and phosphate ion. Control of temperature during the test is very important; the rate of the reaction increases 1.47 times if the temperature changes from 30 °C to 37 °C. What is the activation energy for the ALP–catalyzed conversion of PNPP to PNP and phosphate?
- Solution
-
43.0 kJ/mol
Q12.5.12
In terms of collision theory, to which of the following is the rate of a chemical reaction proportional?
- the change in free energy per second
- the change in temperature per second
- the number of collisions per second
- the number of product molecules
Q12.5.13
Hydrogen iodide, HI, decomposes in the gas phase to produce hydrogen, H2, and iodine, I2. The value of the rate constant, k, for the reaction was measured at several different temperatures and the data are shown here:
| Temperature (K) | k (M−1 s−1) |
|---|---|
| 555 | 6.23 × 10−7 |
| 575 | 2.42 × 10−6 |
| 645 | 1.44 × 10−4 |
| 700 | 2.01 × 10−3 |
What is the value of the activation energy (in kJ/mol) for this reaction?
- Solution
-
177 kJ/mol
Q12.5.14
The element Co exists in two oxidation states, Co(II) and Co(III), and the ions form many complexes. The rate at which one of the complexes of Co(III) was reduced by Fe(II) in water was measured. Determine the activation energy of the reaction from the following data:
| T (K) | k (s−1) |
|---|---|
| 293 | 0.054 |
| 298 | 0.100 |
Q12.5.15
The hydrolysis of the sugar sucrose to the sugars glucose and fructose,
\[\ce{C12H22O11 + H2O ⟶ C6H12O6 + C6H12O6}\nonumber \]
follows a first-order rate equation for the disappearance of sucrose: Rate = k[C12H22O11] (The products of the reaction, glucose and fructose, have the same molecular formulas but differ in the arrangement of the atoms in their molecules.)
- In neutral solution, k = 2.1 × 10−11 s−1 at 27 °C and 8.5 × 10−11 s−1 at 37 °C. Determine the activation energy, the frequency factor, and the rate constant for this equation at 47 °C (assuming the kinetics remain consistent with the Arrhenius equation at this temperature).
- When a solution of sucrose with an initial concentration of 0.150 M reaches equilibrium, the concentration of sucrose is 1.65 × 10−7 M. How long will it take the solution to reach equilibrium at 27 °C in the absence of a catalyst? Because the concentration of sucrose at equilibrium is so low, assume that the reaction is irreversible.
- Why does assuming that the reaction is irreversible simplify the calculation in part (b)?
- Solution
-
Ea = 108 kJ
A = 2.0 × 108 s−1
k = 3.2 × 10−10 s−1
(b) 1.81 × 108 h or 7.6 × 106 day. (c) Assuming that the reaction is irreversible simplifies the calculation because we do not have to account for any reactant that, having been converted to product, returns to the original state.
Q12.5.16
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “straight shot” default option, try launching the A atom with varying amounts of energy. What changes when the Total Energy line at launch is below the transition state of the Potential Energy line? Why? What happens when it is above the transition state? Why?
Q12.5.17
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “angled shot” option, try launching the A atom with varying angles, but with more Total energy than the transition state. What happens when the A atom hits the BC molecule from different directions? Why?
- Solution
-
The A atom has enough energy to react with BC; however, the different angles at which it bounces off of BC without reacting indicate that the orientation of the molecule is an important part of the reaction kinetics and determines whether a reaction will occur.
12.6: Reaction Mechanisms
Q12.6.1
Why are elementary reactions involving three or more reactants very uncommon?
Q12.6.2
In general, can we predict the effect of doubling the concentration of A on the rate of the overall reaction \(A+B⟶C\) ? Can we predict the effect if the reaction is known to be an elementary reaction?
- Solution
-
Add texts here. Do not delete this text first.
No. In general, for the overall reaction, we cannot predict the effect of changing the concentration without knowing the rate equation. Yes. If the reaction is an elementary reaction, then doubling the concentration of A doubles the rate.
Q12.6.3
Phosgene, COCl2, one of the poison gases used during World War I, is formed from chlorine and carbon monoxide. The mechanism is thought to proceed by:
| step 1: | Cl + CO → COCl |
| step 2: | COCl + Cl2→ COCl2 + Cl |
- Write the overall reaction equation.
- Identify any reaction intermediates.
- Identify any intermediates.
Q12.6.4
Define these terms:
- unimolecular reaction
- bimolecular reaction
- elementary reaction
- overall reaction
Q12.6.5
What is the rate equation for the elementary termolecular reaction \(A+2B⟶\ce{products}\)? For \(3A⟶\ce{products}\)?
- Solution
-
Add texts here. Do not delete this text first.
We are given that both of these reactions are elementary termolecular. The molecularity of a reaction refers to the number of reactant particles that react together with the proper and energy and orientation. Termolecular reactions have three atoms to collide simultaneously. As it is termolecular, and there are no additional reactants aside from the three given in each reaction, there are no intermediate reactions. The rate law for elementary reactions is determined by the stoichiometry of the reaction without needed experimental data.
The basic rate form for the elementary step is what follows:
\(rate= {k} \cdot {reactant \ 1}^{i} \cdot {reactant \ 2}^{ii} \cdot ... \) Where i and ii are the stochiometric coefficient from reactant 1 and 2 respectively.
For: \(3A \rightarrow products \)
\({k} \cdot {A}^3 = rate\)
For: \(A + 2B \rightarrow products \)
\({k} \cdot {[A]} \cdot {[B]}^2 = rate\)
Note that the order of these reactions are both three.
- Answer
-
Add texts here. Do not delete this text first.
Rate = k[A][B]2; Rate = k[A]3
Q12.6.6
Given the following reactions and the corresponding rate laws, in which of the reactions might the elementary reaction and the overall reaction be the same?
(a) \(\ce{Cl2 + CO ⟶ Cl2CO}\)
\(\ce{rate}=k\ce{[Cl2]^{3/2}[CO]}\)
(b) \(\ce{PCl3 + Cl2 ⟶ PCl5}\)
\(\ce{rate}=k\ce{[PCl3][Cl2]}\)
(c) \(\ce{2NO + H2 ⟶ N2 + H2O}\)
\(\ce{rate}=k\ce{[NO][H2]}\)
(d) \(\ce{2NO + O2 ⟶ 2NO2}\)
\(\ce{rate}=k\ce{[NO]^2[O2]}\)
(e) \(\ce{NO + O3 ⟶ NO2 + O2}\)
\(\ce{rate}=k\ce{[NO][O3]}\)
- Solution
-
Add texts here. Do not delete this text first.
An elementary reaction is a chemical reaction in which the reactants directly form products in a single step. In another words, the rate law for the overall reaction is same as experimentally found rate law. Out of 5 options, option (b),(d), and (e) are such reactions
Q12.6.7
Write the rate equation for each of the following elementary reactions:
- \(\ce{O3 \xrightarrow{sunlight} O2 + O}\)
- \(\ce{O3 + Cl ⟶ O2 + ClO}\)
- \(\ce{ClO + O⟶ Cl + O2}\)
- \(\ce{O3 + NO ⟶ NO2 + O2}\)
- \(\ce{NO2 + O ⟶ NO + O2}\)
- Solution
-
Add texts here. Do not delete this text first.
Rate equations are dependent on the reactants and not the products.
The rate law of a reaction can be found using a rate constant (which is found experimentally), and the initial concentrations of reactants.
A general solution for the equation
\(aA + bB \rightarrow cC + dD\)
is \(rate = k[A]^{m}[B]^{n}\) where m and n are reaction orders.
However, reaction orders are found experimentally, and since we do not have experimental data for these reactions, we can disregard that part of the equation.
To find the rate laws, all we have to do is plug the reactants into the rate formula. This is only due to the case that these are elementary reactions. Further reading on elementary reactions can be found on Libre Texts.
a. O3 ⟶ O2 + O
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3]
b. O3 + Cl ⟶ O2 + ClO
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][Cl]
c. ClO + O ⟶ Cl + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[ClO][O]
d. O3 + NO ⟶ NO2 + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][NO]
e. NO2 + O ⟶ NO + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[NO2][O]
- Answer
-
Add texts here. Do not delete this text first.
(a) Rate1 = k[O3]; (b) Rate2 = k[O3][Cl]; (c) Rate3 = k[ClO][O]; (d) Rate2 = k[O3][NO]; (e) Rate3 = k[NO2][O]
Q12.6.8
Nitrogen(II) oxide, NO, reacts with hydrogen, H2, according to the following equation:
\[\ce{2NO + 2H2 ⟶ N2 + 2H2O}\nonumber \]
What would the rate law be if the mechanism for this reaction were:
\[\ce{2NO + H2 ⟶ N2 + H2O2\:(slow)}\nonumber \]
\[\ce{H2O2 + H2 ⟶ 2H2O\:(fast)}\nonumber \]
The rate law of the mechanism is determined by the slow step of the reaction. Since the slow step is an elementary step, the rate law can be drawn from the coefficients of the chemical equation. So therefore, the rate law is as follows: rate=k[NO]2[H2]. Since both NO and H2 are reactants in the overall reaction (therefore are not intermediates in the reaction), no further steps have to be done to determine the rate law.
Q12.6.9
Consider the reaction
CH4 + Cl2 → CH3Cl + HCl (occurs under light)
The mechanism is a chain reaction involving Cl atoms and CH3 radicals. Which of the following steps does not terminate this chain reaction?
- CH3 + Cl → CH3CI
- CH3 + HCl → CH4 + Cl
- CH3 + CH3 → C2H2
- Cl + Cl → Cl2
- Solution
-
Add texts here. Do not delete this text first.
Chain reactions involve reactions that create products necessary for more reactions to occur. In this case, a reaction step will continue the chain reaction if a radical is generated. Radicals are highly reactive particles, so more reactions in the chain will take place as long as they are present. The chlorine is considered a free radical as it has an unpaired electron; for this reason it is very reactive and propagates a chain reaction. It does so by taking an electron from a stable molecule and making that molecule reactive, and that molecule goes on to react with stable species, and in that manner a long series of "chain" reactions are initiated. A chlorine radical will continue the chain by completing the following reaction:
\({Cl \cdot}+{CH_4} \rightarrow {CH_3 \cdot}+{HCl} \)
The \({CH_3}\) generated by this reaction can then react with other species, continuing to propagate the chain reaction.
Option 1 is incorrect because the only species it produces is \({CH_3Cl}\), a product in the overall reaction that is unreactive. This terminates the chain reaction because it fails to produce any \(Cl\) or \(CH_3\) radicals that are necessary for further propagating the overall reaction.
Option 2 is the correct answer because it produces a \(Cl\) radical. This \(Cl\) radical can continue the chain by colliding with \(CH_4\) molecules.
Option 3 is incorrect because it fails to produce a radical capable of continuing the chain.
Option 4 is incorrect because it produces \(Cl_2\), a molecule that does not react unless additional light is supplied. Therefore, this step breaks the chain.
- Answer
-
Add texts here. Do not delete this text first.
Answer: Option 2: \({CH_3}+{HCl} \rightarrow {CH_4}+{Cl}\)
Q12.6.10
Experiments were conducted to study the rate of the reaction represented by this equation.
\[\ce{2NO}(g)+\ce{2H2}(g)⟶\ce{N2}(g)+\ce{2H2O}(g)\nonumber \]
Initial concentrations and rates of reaction are given here.
| Experiment | Initial Concentration [NO] (mol/L) | Initial Concentration, [H2] (mol/L) | Initial Rate of Formation of N2 (mol/L min) |
|---|---|---|---|
| 1 | 0.0060 | 0.0010 | 1.8 × 10−4 |
| 2 | 0.0060 | 0.0020 | 3.6 × 10−4 |
| 3 | 0.0010 | 0.0060 | 0.30 × 10−4 |
| 4 | 0.0020 | 0.0060 | 1.2 × 10−4 |
Consider the following questions:
- Determine the order for each of the reactants, NO and H2, from the data given and show your reasoning.
- Write the overall rate law for the reaction.
- Calculate the value of the rate constant, k, for the reaction. Include units.
- For experiment 2, calculate the concentration of NO remaining when exactly one-half of the original amount of H2 had been consumed.
- The following sequence of elementary steps is a proposed mechanism for the reaction.
Step 1: \(\ce{NO + NO ⇌ N2O2}\)
Step 2: \(\ce{N2O2 + H2 ⇌ H2O + N2O}\)
Step 3: \(\ce{N2O + H2 ⇌ N2 + H2O}\)
Based on the data presented, which of these is the rate determining step? Show that the mechanism is consistent with the observed rate law for the reaction and the overall stoichiometry of the reaction.
S12.6.10
1. i) Find the order for [NO] by using experiment 3 and 4 where [H2] is constant
Notice that [NO] doubles from experiment 3 to 4 and the rate quadruples. So the order for [NO] is 2
ii) Find the order for [H2] by using experiment 1 and 2 where [NO] is constant
Notice that [H2] doubles from experiment 1 to 2 and the rate doubles as well. So the order for [H2] is 1
2. Put in the order for each product as the exponents for the corresponding reactant.
\(rate = k [NO]^2 [H_2]\)
3. Put in the concentrations and the rate from one of the experiments into the rate law and solve for k. (Here, experiement 1 is used but any of them will work)
\(rate = k [NO]^2 [H_2]\) \(.00018 = k [.006]^2 [.001]\) \(k = 5000 M^{-2}s^{-1}\)
4. Plug in values for experiment 2 into the rate law equation and solve for the concentration of NO
\(.00036=5000[NO]^2[.001]\) \([NO]^2= 7.2 x 10^{-5}\) \([NO] = .0085 M\)
5. Write the rate laws for each step and then see which matches the rate law we found in question 2. The rate determining step (the slow step) is the one that gives the rate for the overall reaction. Because of this, only those concentrations will influence the overall reaction, contrary to what we would believe if we just looked at the overall reaction.
Step 1: \(NO + NO \rightleftharpoons N_2O_2\)
\(rate =k_1[NO]^2\) This rate law is not the same as the one we calculate in question 2 so this can not be the rate determining step
Step 2: \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\)
\(rate = k_2[N_2O_2][H_2]\)
Since \(N_2O_2\) is an intermediate you must replace it in the rate law equation. Intermediates can not be in the rate law because they do not appear in the overall reaction. Here you can take the reverse of equation 1 (k-1) and substitute the other side (the reactants of equation 1) for the intermediate in the rate law equation.
\[rate_1 = rate_{-1}\nonumber \]
\[k_1[NO]^2 = k_{-1}[N_2O_2]\nonumber \]
\[[N_2O_2] = \frac{k_1[NO]^2}{k_{-1}}\nonumber \]
\(rate= \frac{k_2k_{1}[NO]^2[H_2]}{k_{-1}}\)
Overall: \(rate={k[NO]^2[H_2]}\) This is the same so it is the rate determining step.
So \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\) is the rate determining step step.
- Answer
-
Add texts here. Do not delete this text first.
(a) NO: 2
\(\ce {H2}\) : 1
(b) Rate = k [NO]2[H2];
(c) k = 5.0 × 103 mol−2 L−2 min−1;
(d) 0.0050 mol/L;
(e) Step II is the rate-determining step.
Q12.6.11
The reaction of CO with Cl2 gives phosgene (COCl2), a nerve gas that was used in World War I. Use the mechanism shown here to complete the following exercises:
- \(\ce{Cl2}(g)⇌\ce{2Cl}(g)\) (fast, k1 represents the forward rate constant, k−1 the reverse rate constant)
- \(\ce{CO}(g)+\ce{Cl}(g)⟶\ce{COCl}(g)\) (slow, k2 the rate constant)
- \(\ce{COCl}(g)+\ce{Cl}(g)⟶\ce{COCl2}(g)\) (fast, k3 the rate constant)
- Write the overall reaction.
- Identify all intermediates.
- Write the rate law for each elementary reaction.
- Write the overall rate law expression.
- Solution
-
Add texts here. Do not delete this text first.
1. To write the overall reaction you have to identify the intermediates and leave them out. The easiest way to do this is to write out all the products and reactants and cross out anything that is on both sides.
Cl2(g) + CO(g) + 2Cl(g) +COCl(g) ⇒ 2Cl(g) + COCl(g) + COCl2(g)
In this you will cross out the 2Cl(g) molecules and the COCl(g). What is left after that is the overall reaction.
Cl2(g) + CO(g) ⇒ + COCl2(g)
2. For part two you will just list the intermediates that you crossed out.
Cl and COCl are intermediates
3. Each rate law will be the rate equal to the rate constant times the concentrations of the reactants
reaction 1
(forward) rate=k1[Cl2] ( reverse) rate=k-1[Cl]
reaction 2
rate=k2[CO][Cl]
Reaction 3
rate=k3[COCl][Cl]
4. The overall rate law is based off the slowest step (step #2), since it is the rate determining step, but Cl is present in that rate law so we have to replace it with an equivalent that does not contain an intermediate. To do this you use the equilibrium since the rates are the same you can set up the rate laws of the forward and reverse equal to each other.
k1[Cl2] = k-1[Cl]
[Cl]= k1[Cl2]/k-1
rate=k2[CO]k1[Cl2]/k-1
rate=k°[CO][Cl2]
Steps to replacing and intermediate
- Set the forward and reverse reaction equal to each other using separate constants
- Solve for the intermediate using algebra
- Plug into the rate determining formula
- All the k's will be condensed into a K prime constant
12.7: Catalysis
Q12.7.1
Account for the increase in reaction rate brought about by a catalyst.
Q12.7.2
Compare the functions of homogeneous and heterogeneous catalysts.
Q12.7.3
Consider this scenario and answer the following questions: Chlorine atoms resulting from decomposition of chlorofluoromethanes, such as CCl2F2, catalyze the decomposition of ozone in the atmosphere. One simplified mechanism for the decomposition is: \[\ce{O3 \xrightarrow{sunlight} O2 + O}\\ \ce{O3 + Cl ⟶ O2 + ClO}\\ \ce{ClO + O ⟶ Cl + O2}\nonumber \]
- Explain why chlorine atoms are catalysts in the gas-phase transformation: \[\ce{2O3⟶3O2}\nonumber \]
- Nitric oxide is also involved in the decomposition of ozone by the mechanism: \[\ce{O3 \xrightarrow{sunlight} O2 + O\\ O3 + NO ⟶ NO2 + O2\\ NO2 + O ⟶ NO + O2}\nonumber \]
Is NO a catalyst for the decomposition? Explain your answer.
Q12.7.4
For each of the following pairs of reaction diagrams, identify which of the pair is catalyzed:
(a)
Q12.7.5
For each of the following pairs of reaction diagrams, identify which of the pairs is catalyzed:
(a)
(b)
Q12.7.6
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)
(b)
Q12.7.7
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)

(b)
Q12.7.8
- Based on the diagrams in Question Q12.7.6, which of the reactions has the fastest rate? Which has the slowest rate?
- Based on the diagrams in Question Q12.7.7, which of the reactions has the fastest rate? Which has the slowest rate?



![{\ displaystyle t_ {\ frac {1} {2}} = {\ frac {1} {k {\ ce {[A] 0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b25f9b5e7675b3e3f9027241a74ec2d751810c43)