Skip to main content
Global

10.2 : Résolution et représentation graphique des inégalités, et rédaction de réponses en notation par intervalles

  1. Last updated
  2. Save as PDF
  • Page ID
    165934

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pour résoudre et représenter graphiquement les inégalités :

    1. Résolvez l'inégalité à l'aide des propriétés des inégalités de la section précédente.
    2. Représentez graphiquement l'ensemble de solutions sur une ligne numérique.
    3. Écrivez l'ensemble de solutions en notation par intervalles.
    Exemple Template:index

    Résolvez l'inégalité, représentez graphiquement l'ensemble de solutions sur une ligne numérique et affichez l'ensemble de solutions en notation par intervalles :

    1. \(−1 ≤ 2x − 5 < 7\)
    2. \(x^2 + 7x + 10 < 0\)
    3. \(−6 < x − 2 < 4\)
    Solution
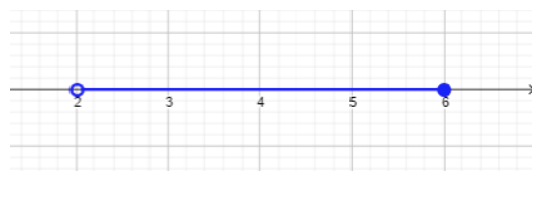
    1. \(\begin{array} &&−1 ≤ 2x − 5 < 7 &\text{Example problem} \\ &−1 + 5 ≤ 2x − 5 + 5 < 7 + 5 &\text{The goal is to isolate the variable \(x\), commencez donc par ajouter\(5\) aux trois régions de l'inégalité.} \ \ &4 ≤ 2x < 12 & \ text {Simplifier.} \ \ & \ dfrac {4} {2} ≤ 2x^2 < \ dfrac {4} {2} & \ text {Divisez le tout par\(2\) pour isoler la variable\(x\).} \ \ &2 ≤ x < 6 & \ text {Réponse finale écrite en forme d'ensemble d'inégalités/solutions.} \ \ & [2, 6) & \ text {Réponse finale écrite en notation par intervalles (voir la section sur la notation par intervalles pour plus de détails)} \ end {array} \)

    clipboard_efc0262004238b3445893f014c353f830.png

    1. \(\begin{array} &&x^2 + 7x + 10 < 0 &\text{Example problem} \\ &(x + 5)(x + 2) < 0 &\text{Factor the polynomial.} \\ &(x + 5)(x + 2) < 0 &\text{The product must be less than \(0\), ce qui signifie que si\((x + 5) > 0\), alors\((x + 2) < 0\). De même\((x + 5) < 0\), si, alors\((x + 2) > 0\).} \ \ & (x + 5) > 0 (x + 2) < 0 & \ text {Find the intersection of each of these inequalities.} \ \ &x > −5 x < −2 & \ text {Trouvez l'intersection de chacune de ces inégalités.} \ end {tableau} \)
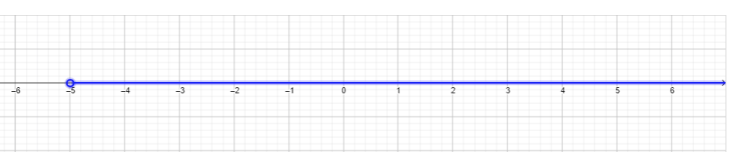
    clipboard_e1db3296d32ab4a7d251b8253c3b147d0.png
    Kit de solutions pour\(x > −5\).
    clipboard_e9ed6522e3f219b2195a81e9a9f3a9253.png
    Kit de solutions pour\(x − 2\).

    \(\begin{array} &&\;\;\;−5 < x < −2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\text{Final answer written in inequality/solution set form.} \\ &\;\;\;(−5, −2) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\text{Final answer written in interval notation (see section on Interval Notation for more details).} \end{array}\)

    1. \(\begin{array}&&−6 < x − 2 ≤ 4 &\text{Example problem} \\ &−6 + 2 < x − 2 + 2 ≤ 4 + 2 &\text{The goal is to isolate the variable \(x\), commencez donc par ajouter\(2\) aux trois régions de l'inégalité.} \ \ &−4 < x ≤ 6 & \ text {Réponse finale écrite sous forme d'inégalité/ensemble de solutions.} \ \ & (−4, 6] & \ text {Réponse finale écrite en notation par intervalles (voir la section sur la notation par intervalles pour plus de détails).} \ end {tableau} \)

    clipboard_e61db0750eee74347f74804dbd4b7221a.png

    Exercice Template:index

    Résolvez les inégalités, représentez graphiquement les ensembles de solutions sur une ligne numérique et affichez les ensembles de solutions en notation par intervalles :

    1. \(0 ≤ x + 1 ≤ 4\)
    2. \(0 < 2(x − 1) ≤ 4\)
    3. \(6 < 2(x − 1) < 12\)
    4. \(x^2 − 6x − 16 < 0\)
    5. \(2x^2 − x − 15 > 0\)