7.1 : Pente d'une ligne
- Page ID
- 165672
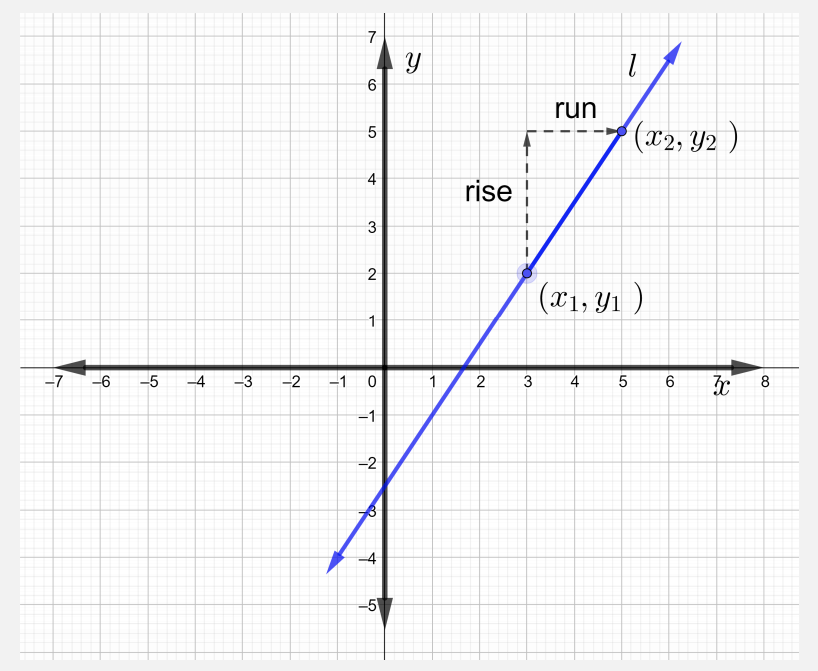
N'oubliez pas que les paires ordonnées peuvent être représentées graphiquement sous forme de points dans le plan de coordonnées rectangulaire. À travers deux points distincts, tracez une ligne droite,\(l\).
Pour décrire une droite de manière\(l\) algébrique, considérez d'abord la pente d'une formule linéaire.
La pente\(m\) d'une ligne\(l\) qui passe par des points\((x_1, y_1)\) et\((x_2, y_2)\) est
\[m = \dfrac{\text{rise}}{\text{run}} = \dfrac{y_2 − y_1}{x_2 − x_1} \text{ where } x_2 \neq x_1 \nonumber \]
Déterminez la pente de la ligne dans la figure ci-dessous.
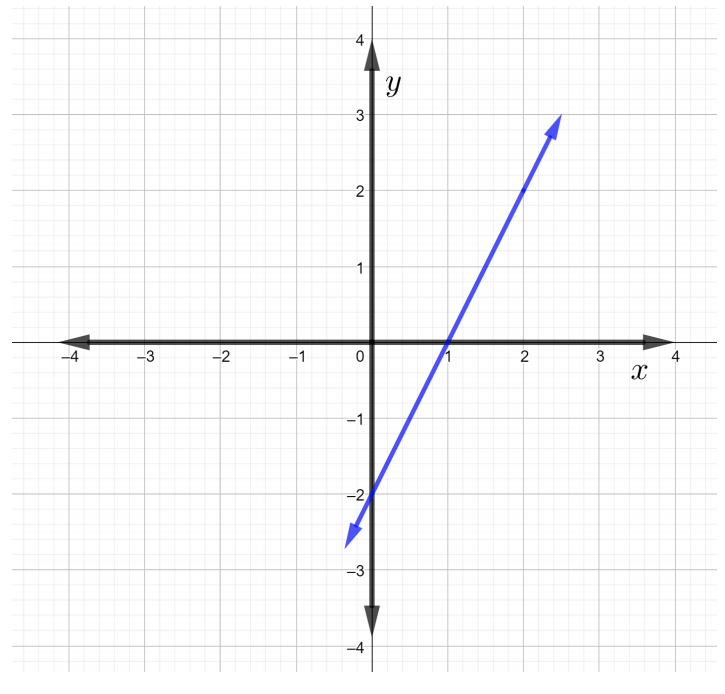
Solution
Selon la définition ci-dessus de la pente de la formule de droite, la pente de la droite peut être écrite comme\(m = \dfrac{\text{rise}}{\text{run}}\). Commencez par choisir deux points,\(P\) et\(Q\), sur la ligne. Choisissez le point\(P\) à être\((2, 2)\) et le point\(Q\) à être\((1, 0)\).
En commençant par le point\(Q\), montez jusqu'au point\(P\) en comptant les carrés de la\(2\) grille vers le haut, ce qui signifie\(\text{rise} = 2\). Maintenant, pour arriver au point\(P\),\(\text{run}\)\(1\) quadrillage vers la droite, ce qui signifie que\(\text{run} = 1\), comme le montre la figure ci-dessous.
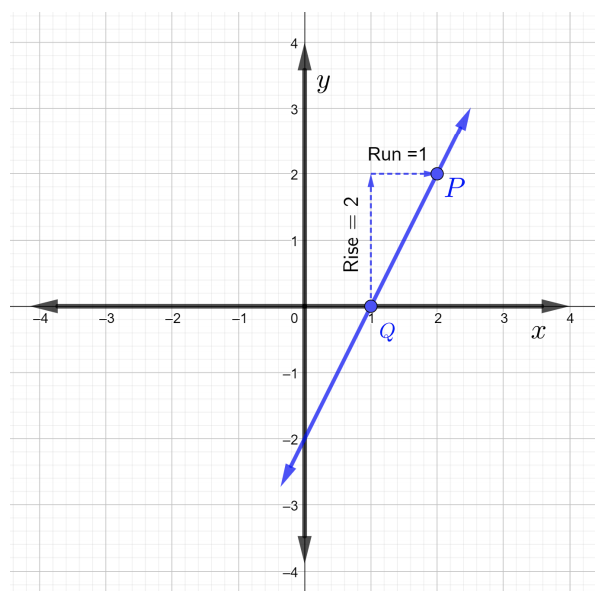
Ainsi,
\(\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{2}{1} &\text{rise \(2\)et exécutez\(1\)} \ \ &= 2 \ end {array} \)
Par conséquent, la pente de la ligne sur la figure est\(m = 2\).
Déterminez la pente de la ligne illustrée dans la figure ci-dessous.
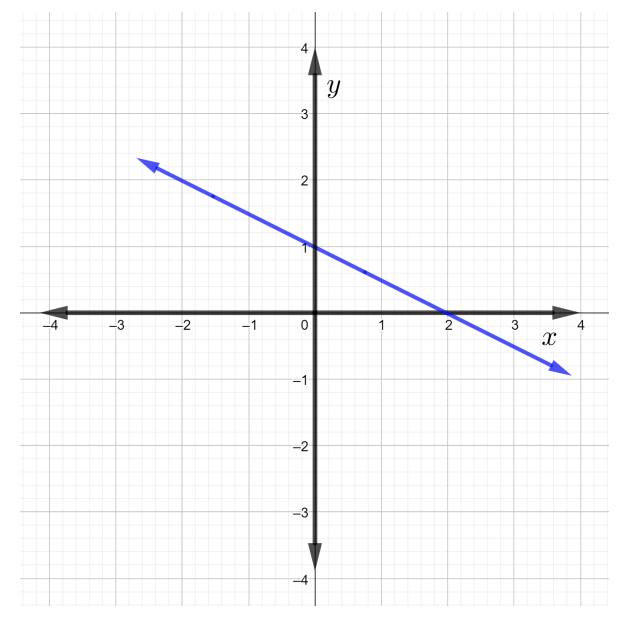
Solution
Comme dans Exemple\(1\), commencez par choisir deux points,\(P\) et\(Q\), sur la ligne.
Remarque : Comme tous les\(2\) points de la ligne peuvent être sélectionnés, il sera plus facile de choisir les deux points qui sont des entiers. Ces points sont situés sur la ligne et également à l'intersection de deux lignes de la grille. Par exemple, sur la figure, il sera plus facile de choisir deux des points suivants sur la ligne donnée :\((2, 0)\),,\((0, 1)\),\((4, −1)\),\((6, −2)\),\((−4, 3)\)\((−6, 4)\), et ainsi de suite...
La pente est la même pour deux points\(P\) et\(Q\) sur la ligne. Choisissez le point\(P_1\) à être\((0, 1)\) et le point\(Q_1\) à être\((2, 0)\). À partir du point\(P_1\), atteignez le point\(Q_1\) en faisant d'abord\(2\) défiler les cases de la grille vers la droite, ce qui signifie que le\(\text{run} = 2\). Maintenant, pour arriver au\(Q_1\) nombre de points, carré de la\(1\) grille vers le bas. Notez que cela\(\text{rise} = -1\) signifie descendre l'\(1\)unité comme indiqué dans la figure ci-dessous.
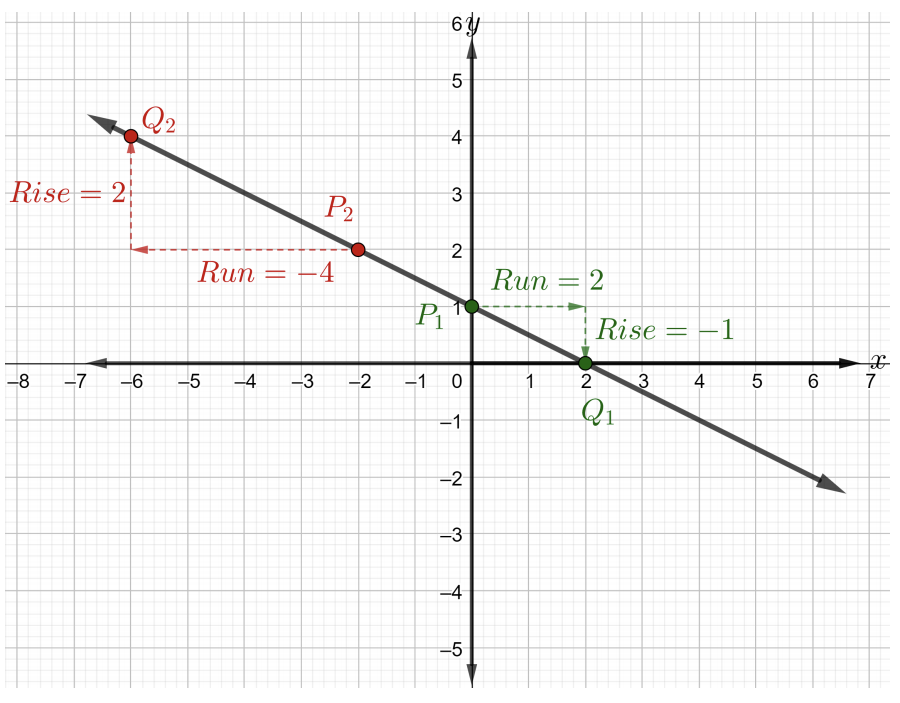
\(\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{−1}{2} &\text{rise = \(-1\)et exécutez =\(2\)} \ end {array} \)
Par conséquent, la pente de la ligne dans la figure ci-dessus est\(m = −\dfrac{1}{2}\).
Maintenant, choisissez le point\(P_2\) à être\((-2, 2)\) et le point\(Q_2\) à être\((-6, 4)\) comme indiqué dans la figure ci-dessus. En commençant par des points\(P_2\), atteignez le point\(Q_2\) en faisant d'abord\(4\) défiler les cases de la grille vers la gauche, ce qui signifie que le\(\text{run} = -4\). Maintenant, pour arriver à\(Q_2\) compter les carrés de la\(2\) grille vers le haut, comptez Ainsi, le\(\text{rise} = 2\). La pente est\(m = \dfrac{2}{−4} = −\dfrac{1}{2}\). Notez que la pente est la même quels que soient les\(2\) points que nous considérons sur une ligne donnée.
Déterminez la pente de la ligne qui la traverse\((3, 2)\) et\((4, 4)\) utilisez la formule de pente. Tracez la ligne qui passe par les points donnés.
Remarque : L'ordre dans lequel les points sont étiquetés ne changera pas la pente d'une formule linéaire tant qu'elle est cohérente.
Solution
Laissez\((x_1, y_1) = (3, 2)\) et\((x_2, y_2) = (4, 4)\) ensuite,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{4 − 2}{4 − 3} & \\ &= \dfrac{2}{1} &\text{rise \(= 2\)et exécutez\(= 1\)} \ \ &= 2 & \ end {array} \)
Par conséquent, la pente de la ligne passant par les points\((3, 2)\) et\((4, 4)\) est\(m = 2\). La ligne qui passe par les points donnés est illustrée dans la figure ci-dessous.
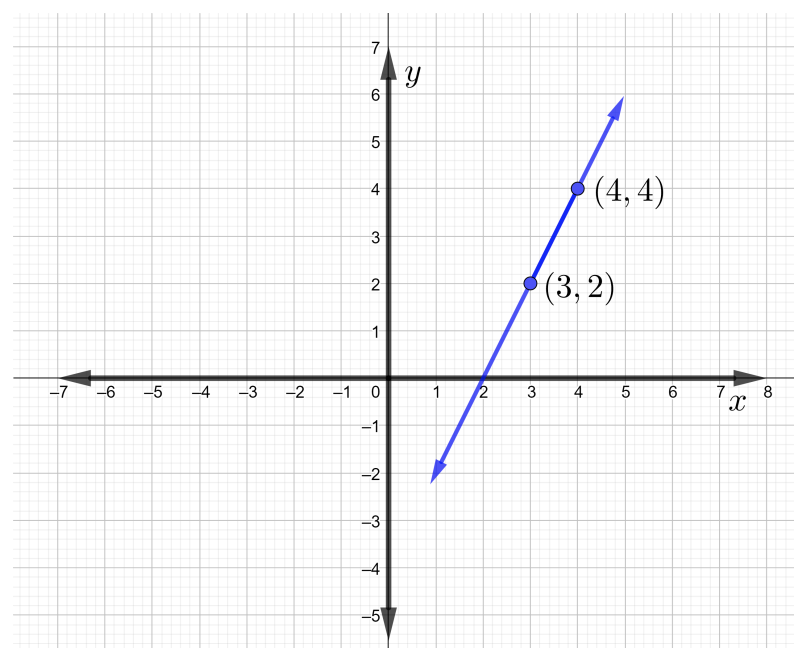
Notez que lorsque la ligne s'élève de gauche à droite, elle présente une pente positive.
Déterminez la pente de la ligne qui passe par les points\((−1, 2)\) et\((3, −4)\). Tracez les points et tracez la ligne.
Solution
Laissez\((x_1, y_1) = (-1, 2)\) et\((x_2, y_2) = (3, -4)\) ensuite,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{-4 − 2}{3 − (-1)} & \\ &= \dfrac{-6}{4} &\text{Simplify} \\ &= -\dfrac{3}{2} & \end{array}\)
Maintenant, pour tracer la ligne passant par les points donnés, tracez d'abord les deux points, puis tracez une ligne droite à travers eux, comme le montre la figure ci-dessous.
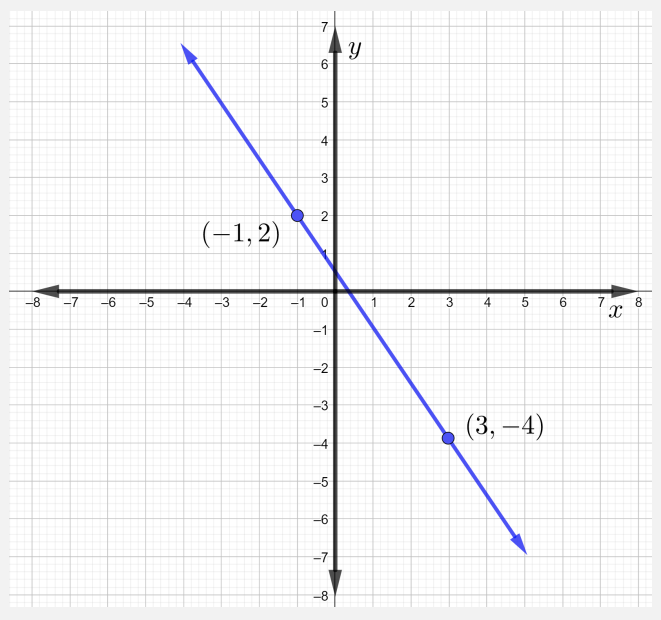
Notez que lorsque la ligne tombe de gauche à droite, elle présente une pente négative.
Trouvez les pentes de chaque droite sur le graphique dans Problèmes\(1\) à\(4\)
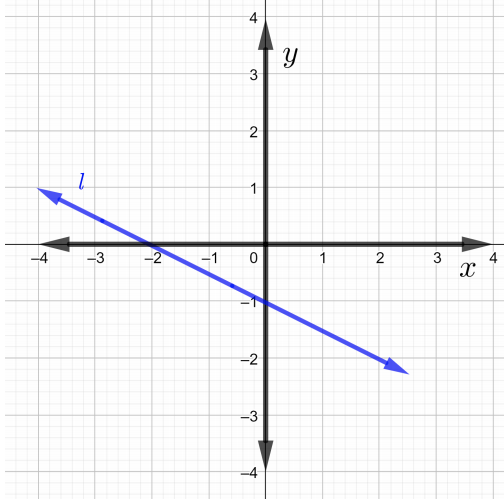
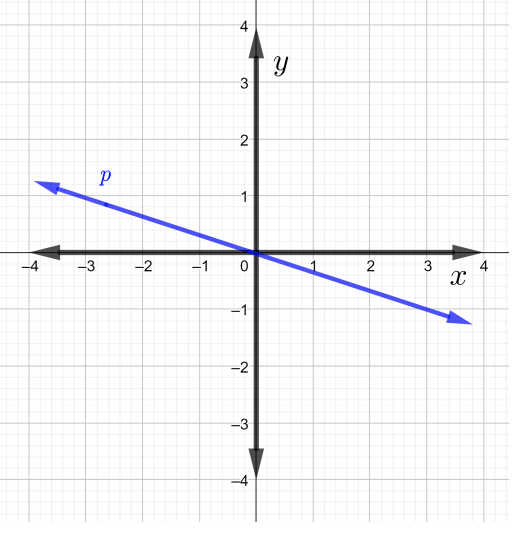
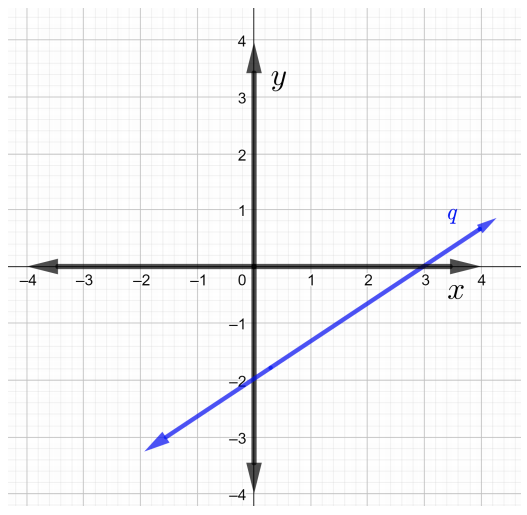
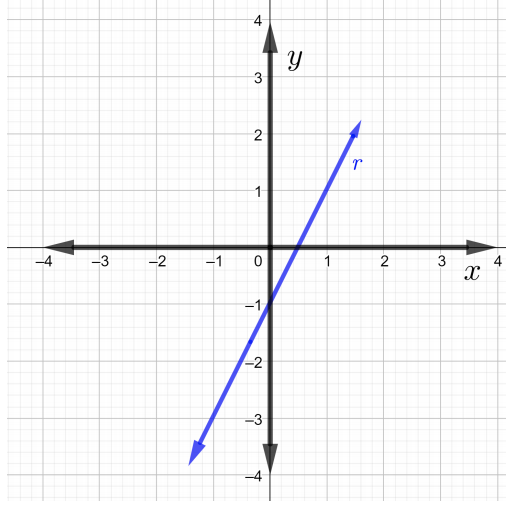
Déterminez la pente de la ligne qui passe par les points donnés dans Problèmes\(5\) traversés\(7\).
- \((−3, 5)\)et\((4, −5)\)
- \((2, 5)\)et\((0, −1)\)
- \((4, 1)\)et\((0, 0)\)


