4.6 : Fonctions polynomiales
- Page ID
- 165755
Une fonction polynomiale est une fonction qui peut être écrite sous la forme générale suivante :
\(f(x) = a_n x^n + a_{n−1} x^{n−1 }+ ... + a_1x + a_0\)
pour\(n\) un entier non négatif, appelé degré du polynôme. Les coefficients\(a_0\),\(a_1\),\(\ldots\), et sont des nombres réels avec le coefficient principal an\(a_n \neq 0\). Le domaine d'une fonction polynomiale est\((−\infty , \infty )\). Le graphe d'une fonction polynomiale de degré\(n\) peut croiser l'axe des abscisses la plupart du\(n\) temps. Ce sont les racines de la fonction polynomiale.
Il n'y a pas d'exemples ni de devoirs dans cette section.
Fonctions quadratiques
\(f(x) = ax^2 + bx + c\)où\(a\neq 0\)
est une fonction quadratique sous forme standard, et son graphe est une parabole. Lorsque le coefficient principal,\(a\), est positif, le graphique de la fonction quadratique s'ouvre vers le haut. Lorsque le coefficient principal,\(a\), est négatif, le graphique de la fonction quadratique s'ouvre vers le bas.
Esquissez un graphe de\(f(x) = −x^2 + 5x + 3\) dans un système de coordonnées rectangulaires. Trouvez algébriquement le sommet, les interceptions x et les interceptions y.
Solution
Trouvez le sommet en calculant\(\left(\dfrac{-b}{2 a}, f\left(\dfrac{-b}{2 a}\right)\right)\) avec\(a = −1\),\(b = 5\) et\(c = 3\).
\ (\ begin {aligné}
\ left (\ dfrac {-b} {2 a}, f \ left (\ dfrac {-b} {2 a} \ right) \ right) &=&& \ text {Trouvez le sommet de la parabole} \ \ \ dfrac {-5} {2} {2} {2} {2} {5}
\ dfrac {5} {2} &=2,5
\ dfrac {5} {2} &=2,5 \ dfrac {5} {Simplifier}
\ \ \ dfrac {-5} {2 (-1)} &=2,5 \ \
f (2,5) &=- (2,5) ^ {2} +5 (2,5) +3=9,25=&& f \ left (\ dfrac {-b} {2 a} \ right) =9,25 \ \ \ gauche (\ dfrac {-b} {2 a}, f \ left (\ dfrac {-b} {2 a} \ right) \ right) & =( 2,5, 9,25) && \ text {Sommet de la parabole}
\ end {aligné} \)
Pour trouver les interceptions :
\ (\ begin {aligné} 0&=-x^ {2} +5 x+3 && \ text {x-intercept, set} f (x) =0 \ \ 0&=-x^ {2} +5 x+3 && \ text {Utilisez la formule quadratique pour résoudre cette équation (elle ne peut pas être factorisée). Soit} a=-1, b=5, c=3 \ \ x&= \ dfrac {-5 \ pm \ sqrt {(5) ^ {2} -4 (-1) (3)}} {2 (-1)} {2 (-1)} && \ text {Formule quadratique
} \ \ x&= \ dfrac {-5 \ pm \ sqrt {37}} {-2} && \ text {Simplifier} \ \
x&=-0,54 \ text {ou} x=5,54 && \ text {Cette fonction quadratique possède deux racines (x-intercepts). } \ \ f (0) &=-0^ {2} +5 (0) +3 && \ text {y-interception, set} x=0 \ \ f (0) &=3 && \ text {y-interception} \ end {aligné} \)
Représentez graphiquement les quatre paires ordonnées et calculez d'autres paires ordonnées si nécessaire :\((2.5, 9.25)\)\((−.54, 0)\),,\((5.54, 0)\),\((0, 3)\).

- \(f(x) = 2x ^2 − 5x − 5\)
- \(f(x) = 0.5x ^2 − 6x + 21\)
- \(f(x) = −4x ^2 − 8x − 3\)
- \(f(x) = −4x^ 2 + 16x − 15\)
- \(f(x) = x^ 2 − 8x + 12\)
- \(f(x) = −7x^ 2 + 100x − 10\)
Fonctions cubiques et d'ordre supérieur
Une fonction cubique est une fonction polynomiale du troisième degré qui peut être écrite sous la forme générale suivante :
\(f(x) = a_3x^ 3 + a_2x^2 + a_1x + a_0\)
avec 3 comme degré de la fonction cubique. Les coefficients\(a_0\),,\(a_1\)\(a_2\),\(a_3\) sont des nombres réels avec un coefficient principal\(a_3 \neq 0\). Le domaine d'une fonction cubique est\((−\infty , \infty )\).
Factoriez si possible et représentez graphiquement la fonction en créant un tableau de solutions :
\(f(x) = x^3 − 4x^2 + 6x − 1\)
Solution
Ce polynôme est de degré 3 et est difficile à factoriser. Créez un tableau de solutions à représenter graphiquement.

| Tableau des solutions pour\(f(x) = x^3 − 4x^2 + 6x − 1\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^3 − 4(−2)^2 + 6(−2) − 1 = −37\) |
| -1 | \(f(−1) = (−1)^3 − 4(−1)^2 + 6(−1) − 1 = −12\) |
| 0 | \(f(0) = (0)^3 − 4(0)^2 + 6(0) − 1 = −1\) |
| 1 | \(f(1) = (1)^3 − 4(1)^2 + 6(1) − 1 = 2\) |
| 2 | \(f(2) = (2)^3 − 4(2)^2 + 6(2) − 1 = 3\) |
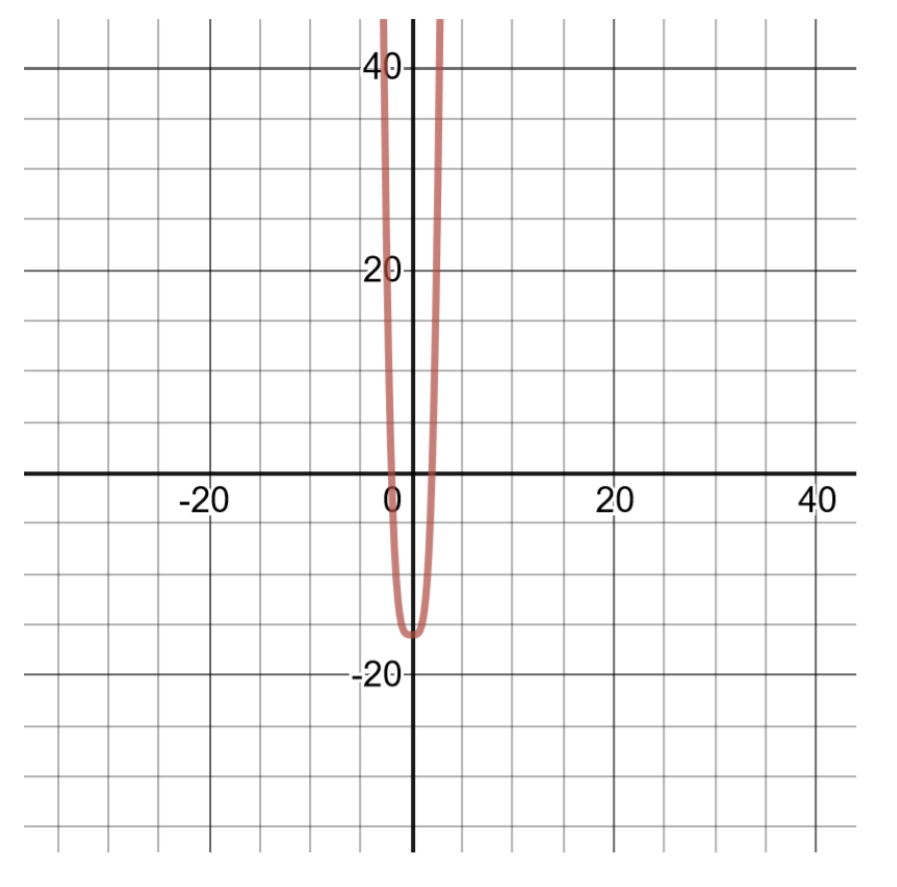
Factoriez si possible et représentez graphiquement la fonction en créant un tableau de solutions :
\(g(x)=x^4-16\)
Solution
Ce polynôme est de degré 4 et, comme il s'agit d'une différence de carrés, il peut être pris en compte dans un produit de binômes pour trouver les zéros du polynôme. Créez un tableau de solutions à représenter graphiquement.
\(\begin{aligned} g(x)&=\left(x^{2}-4\right)\left(x^{2}+4\right) && \text{Factoring into the sum and difference of binomials.} \\ g(x)&=(x-2)(x+2)\left(x^{2}+4\right) && \text{Further factoring. Set each binomial equal to zero to find the real number zeroes of the polynomial.} \\ x-2&=0, x=2 && \text{The first real number zero of the polynomial, }(2,0) \\ x+2&=0, x=-2 &&\text{The second real number zero of the polynomial, } (2,0) \\ x^{2}+4&=0, x^{2}=-4 && \text{The third binomial factor does not produce real number zeroes, } \\ & &&\text{because no number squared can result in a negative value.} \end{aligned}\)
| Tableau des solutions pour\(g(x)=x^4-16\) | |
| \(x\) | \(g(x)\) |
| -2 | \(g(−2) = (−2)^4 − 16 = 16 − 16 = 0\) |
| -1 | \(g(−1) = (−1)^4 − 16 = 1 − 16 = −15\) |
| 0 | \(g(0) = (0)^4 − 16 = 0 − 16 = −16\) |
| 1 | \(g(1) = g(1) = (1)^4 − 16 = 1 − 16 = −15\) |
| 2 | \(g(2) = g(2) = (2)^4 − 16 = 16 − 16 = 0\) |
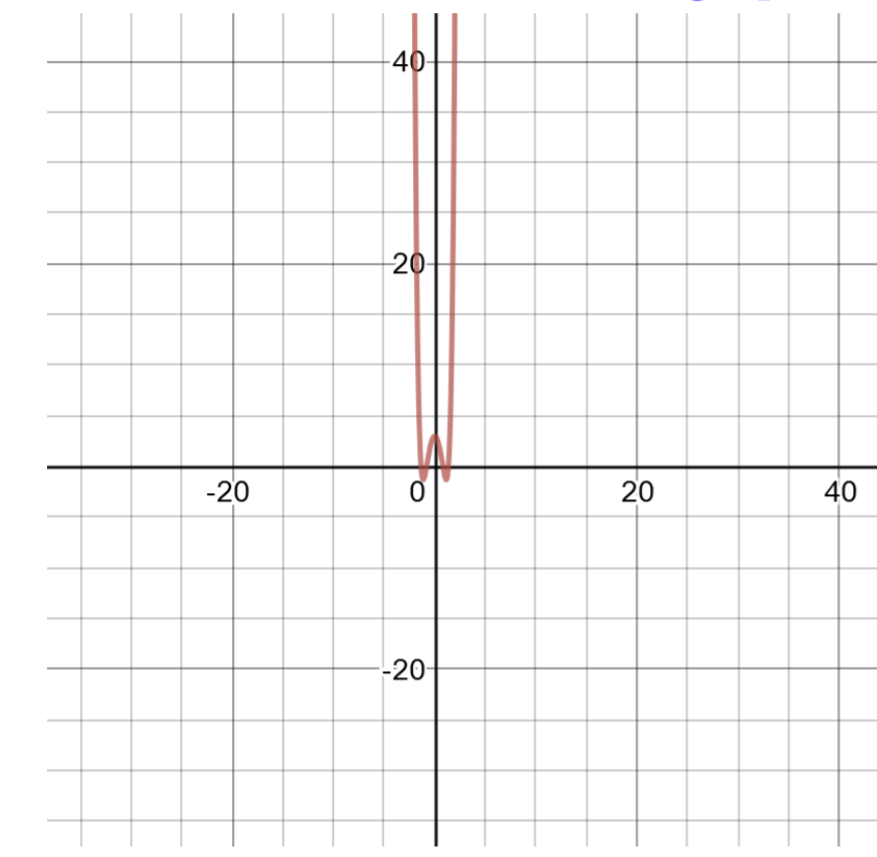
Factoriez si possible et représentez graphiquement la fonction en créant un tableau de solutions :
\(f(x) = x ^6 − 5x ^2 + 3\)
Solution
Ce polynôme est de degré 6 et est difficile à factoriser. Créez un tableau de solutions à représenter graphiquement.
| Tableau des solutions pour\(f(x) = x ^6 − 5x ^2 + 3\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^6 − 5(−2)^2 + 3 = 47\) |
| -1 | \(f(−1) = (−1)^6 − 5(−1)^2 + 3 = −1\) |
| 0 | \(f(0) = (0)^6 − 5(0)^2 + 3 = 3\) |
| 1 | \(f(1) = (1)^6 − 5(1)^2 + 3 = −1\) |
| 2 | \(f(2) = (2)^6 − 5(2)^2 + 3 = 47\) |
- \(f(x) = x^3 − 27\)
- \(g(x) = 81x ^4 − 16\)
- \(h(x) = 2x ^5 − 4x ^2 − 6x + 3\)
- \(f(x) = 5x ^6 − 6x ^4 + 5\)
Fonctions rationnelles
Une fonction rationnelle est une fonction qui peut être écrite sous la forme d'un quotient de polynômes.
\(f(x) = \dfrac{P (x) }{Q(x) }\),\(Q(x) \neq 0\)
où\(P(x)\) et\(Q(x)\) sont des polynômes dans une variable\(x\). Le domaine est l'ensemble de tous les nombres réels tels que\(Q(x) \neq 0\).
Pour la fonction,\(f(x) = \dfrac{9 }{x − 3}\) :
- Tracez la fonction
- Évaluez la fonction pour\(x = 0\) et\(x = 2\)
Solution
Faites attention au domaine de cette fonction. La division par zéro n'étant pas définie, le ou les nombres qui feront du dénominateur 0 doivent être exclus du domaine.
Dans ce problème,\(x − 3\) se trouve dans le dénominateur de la fonction. Définissez\(x − 3 = 0\) et résolvez pour\(x\). Si\(x = 3\) la division n'est pas définie, excluez le numéro 3 du domaine de la fonction. Considérez cela comme toujours en commençant par tous les nombres réels,\((−\infty , \infty )\) puis en supprimant les valeurs qui provoqueront une division indéfinie.
Le domaine de cette fonction est\((−\infty , 3) \cup (3, \infty )\).
Les fonctions rationnelles présentent souvent des asymptotes, c'est-à-dire une droite qui s'approche continuellement d'une courbe donnée mais ne la rejoint à aucune distance finie. Vous découvrirez les asymptotes dans la section Curve Sketching de Math 162.
Le graphique de cette fonction peut être trouvé en faisant un tableau de solutions :

| Tableau des solutions pour\(f(x) = \dfrac{9 }{x − 3}\) | Domaine :\((−\infty , 3) \cup (3, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | \(-\dfrac{9}{7}\) |
| -3 | \(-\dfrac{3}{2}\) |
| -2 | \(-\dfrac{9}{5}\) |
| -1 | \(-\dfrac{9}{4}\) |
| 0 | \(-3\) |
| 1 | \(-\dfrac{9}{2}\) |
| 2 | \(-9\) |
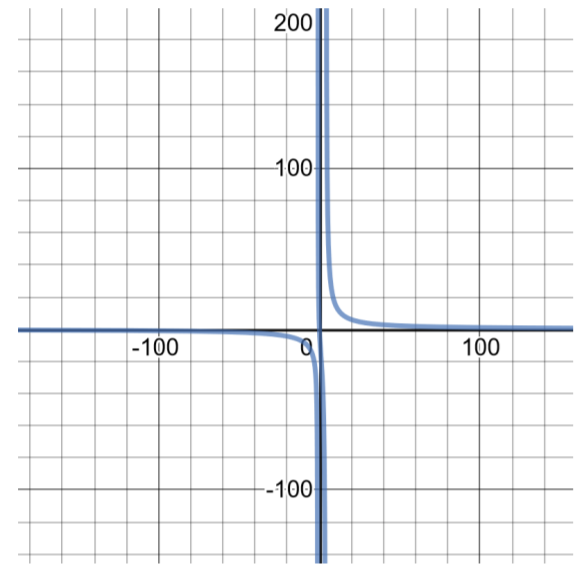
Pour la fonction,\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\)
- Tracez la fonction
- Évaluez la fonction pour\(x = −1\) et\(x = 3\)
Solution
Faites attention au domaine de cette fonction. La division par zéro n'étant pas définie, le ou les nombres qui feront du dénominateur 0 doivent être exclus du domaine.
Dans ce problème,\(x^2 − 3x − 4\) se trouve dans le dénominateur de la fonction. Factoriez l'expression quadratique pour obtenir\((x − 4)(x + 1)\) et définir chaque facteur égal à zéro et résolvez\(x\) :\(x − 4 = 0\), so\(x = 4\) ;\(x + 1 = 0\), so\(x = −1\). Si\(x = 4\) oui\(x = −1\), la division n'est pas définie, excluez donc les nombres 4 et -1 du domaine de la fonction. Considérez cela comme toujours en commençant par tous les nombres réels,\((−\infty , \infty )\) puis en supprimant les valeurs qui entraîneront une division indéfinie.
Le domaine de cette fonction est\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\). Le graphique de cette fonction peut être trouvé en faisant un tableau de solutions :
| Tableau des solutions pour\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\) | Domaine :\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | −16,67 |
| -3 | −21 429 |
| -2 | −33 333 |
| -1 | indéfini |
| 0 | 0 |
| 1 | −16,67 |
| 2 | −33 333 |
| 3 | -75 |
| 4 | indéfini |
- \(f(x) = \dfrac{3x + 6 }{x − 1}\)
- \(f(x) = \dfrac{9 }{x^2 − 9}\)
- \(f(x) = \dfrac{x^ 2 − 4 }{x^2 − 4x}\)


