11.E：粒子物理学和宇宙学（练习）

Last updated
Save as PDF

Page ID: 201940

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

概念性问题

11.1 粒子物理学概论

1。四种基本力量是什么？简要描述它们。

2。使用不可分辨性和交换对称性的概念区分费密子和玻色子。

3。列出夸克和轻子家族

4。区分基本粒子和反粒子。描述他们的互动。

11.2 粒子保护定律

5。什么是六粒子守恒定律？简要描述它们。

6。总的来说，我们如何确定是否发生了粒子反应或衰变？

7。为什么检测违反既定粒子保护定律的粒子相互作用对科学家来说是一件好事？

11.3 夸克

8。已知的六个夸克是什么？总结它们的属性。

9。重子的一般夸克成分是多少？介子的？

10。 有哪些证据证明夸克的存在？

11。 为什么夸克成分相同的重子的静止质量能量有时会有所不同？

11.4 粒子加速器和探测器

12。 简要比较一下 Van de Graaff 加速器、线性加速器、回旋加速器和同步加速器加速器。

13。 描述典型碰撞梁机的基本组件和功能。

14。 紧凑型介子螺线管实验的子探测器有哪些？简要描述它们。

15。 碰撞光束加速器与向固定目标发射粒子的加速器相比有什么优势？

16。 电子出现在 CMS 的μ子探测器中。这怎么可能？

11.5 标准模型

17。 什么是标准模型？用四种基本力和交换粒子来表达你的答案。

18。 画一张费曼图，表示电子和正电子被歼灭成光子。

19。 大统一理论背后的动机是什么？

20。 如果开发出一种理论将所有四种力统一起来，那么说月球的轨道是由引力决定的，还是正确的吗？解释原因。

21。 如果希格斯玻色子被发现并发现有质量，它会被视为弱力的终极载体吗？解释你的回应。

22。 常见的衰减模式之一\(\displaystyle Λ^0\)是\(\displaystyle Λ^0→π^−+p\). 尽管只有强子参与了这种衰变，但它是通过弱核力量发生的。我们怎么知道这种衰变不是通过强大的核力量发生的？

11.6 宇宙大爆炸

23。 宇宙学扩张是什么意思？用哈勃图和遥远星光的红移来表达你的答案。

24。 描述宇宙学扩张的气球类比。解释一下为什么我们似乎只处于宇宙扩张的中心。

25。 与局部星系的距离是通过测量恒星的亮度（称为 Cepheid 变量）来确定的，这些恒星可以单独观测，并且在众所周知的标准距离下具有绝对亮度。解释与绝对亮度相比，测得的亮度将如何随距离而变化。

11.7 早期宇宙的演变

26。 “早期宇宙的宇宙学模型” 是什么意思？用四种基本力简要描述这个模型。

27。 描述支持宇宙大爆炸模型的两个证据。

28。 正如牛顿曾经说过的那样，从什么意义上说，我们是 “一个在海边玩耍的男孩”？用暗物质和暗能量的概念来表达你的答案。

29。 如果发现了某种未知的红移原因，例如光线在空旷空间中长途旅行变得 “疲倦”，那会对宇宙学产生什么影响？

30。 过去，许多科学家认为宇宙是无限的。但是，如果宇宙是无限的，那么任何视线最终都应该落在恒星的表面，夜空应该非常明亮。在现代宇宙学中，这个悖论是如何解决的？

问题

11.1 粒子物理学概论

31。 当静止的电子和正电子相互消灭时，会释放出多少能量？（有关粒子质量，请参见表 11.1。）

32。 如果\(\displaystyle 1.0×10^{30}MeV\)在消灭物质球和反物质时释放了能量，而这些球体的质量相等，那么球体的质量是多少？

33。 当电子和正电子都处于静止状态时，它们可以根据反应相互消灭\(\displaystyle e^−+e^+→γ+γ\)。在这种情况下，每个光子的能量、动量和频率是多少？

34。 随后的衰变粒子带走的总动能是多少？

(a)\(\displaystyle π^0→γ+γ\)

(b)\(\displaystyle K^0→π^++π^−\)

(c)\(\displaystyle \sum{}^+→n+π^+\)

(d)\(\displaystyle \sum{}^0→Λ^0+γ\)。

11.2 粒子保护定律

35。 以下哪种衰变不会因为违反轻子数守恒定律而发生？

(a)\(\displaystyle n→p+e^−\)

(b)\(\displaystyle μ^+→e^++\bar{\nu_e}\)

(c)\(\displaystyle π^+→e^++\nu_e+\bar{\nu_μ}\)

(d)\(\displaystyle p→n+e^++\nu_e\)

(e)\(\displaystyle π^−→e^−+\bar{\nu_e}\)

(f)\(\displaystyle μ^−→e^−+\bar{\nu_e}+\nu_μ\)

(g)\(\displaystyle Λ^0→π^−+p\)

(h)\(\displaystyle K^+→μ^++\nu_μ\)

36。 以下哪种反应不能，因为违反了保护陌生感的法则？

(a)\(\displaystyle p+n→p+p+π^−\)

(b)\(\displaystyle p+n→p+p+K^−\)

(c)\(\displaystyle K^−+p→K^−+\sum{}^+\)

(d)\(\displaystyle π^−+p→K^++\sum{}^−\)

(e)\(\displaystyle K^−+p→Ξ^0+K^++π^−\)

(f)\(\displaystyle K^−+p→Ξ^0+π^−+π^−\)

(g)\(\displaystyle π^++p→\sum{}^++K^+\)

(h)\(\displaystyle π^−+n→K^−+Λ^0\)

37。 确定以下每种反粒子的一种可能的衰变：

(a)\(\displaystyle \bar{n}\)，

(b)\(\displaystyle \bar{Λ^0}\)，

(c)\(\displaystyle Ω^+\)，

(d)\(\displaystyle K^−\)，以及

(e)\(\displaystyle \bar{\sum{}}\)。

38。 禁止以下每种强烈的核反应。确定每项法律中违反的保护法。

(a)\(\displaystyle p+\bar{p}→p+n+\bar{p}\)

(b)\(\displaystyle p+n→p+\bar{p}+n+π^+\)

(c)\(\displaystyle π^−+p→\sum{}^++K^−\)

(d)\(\displaystyle K^−+p→Λ^0+n\)

11.3 夸克

39。 根据质子的夸克构成，证明它的电荷是\(\displaystyle +1\)。

40。 根据中子的夸克成分，显示电荷为 0。

41。 争辩说，表 11.5 中给出的正 kaon 的夸克成分与这个重子的已知电荷、自旋和陌生感一致。

42。 介子由以下夸克组合组成（下标表示颜色和\(\displaystyle (AR=antired): (d_R,\bar{d_{AR}}), (s_G,\bar{u_{AG}})\)、和\(\displaystyle (s_R,\bar{s_{AR}})\)。

(a) 确定每种组合的电荷和奇异性。

(b) 识别每个 quark-antiquark 组合形成的一个或多个介子。

43。 为什么下面显示的任何一组夸克都不能形成强子？

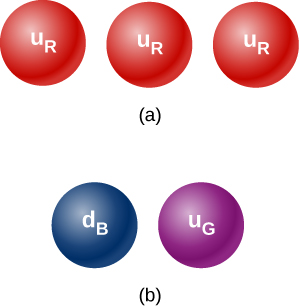
图 a 有三个红色圆圈，每个都标有 u 下标 R。图 b 有一个标有 d 下标 B 的蓝色圆圈和一个标有 u 下标 G 的紫色圆圈

44。 实验结果表明，一个带电荷的分离粒子\(\displaystyle +2/3\) ——一个孤立的夸克。这可能是什么夸克？为什么这个发现很重要？

45。 用夸克的\(\displaystyle β\)衰变\(\displaystyle n→p+e^−+\bar{\nu}\)和\(\displaystyle p→n+e^++\nu\)\(\displaystyle β\)衰变来表达。看看夸克\(\displaystyle β\)衰变是否满足了电荷、轻子数和重子数的保护法规。

11.4 粒子加速器和探测器

46。 2.0-T 磁场中的带电粒子在半径为 75 cm 的圆中弯曲。粒子的动量是多少？

47。 质子轨道穿过半径为 50 cm 的磁场。磁场强度为 1.5 T 质子的总能量是多少？

48。 \(\displaystyle p=0.3Br\)使用向心加速度（二维和三维运动）和相对论动量（相对论）的概念推导方程

49。 假设电子-正电子对撞机的光束能量约为 4.73 GeV。在这个对撞机中消灭电子和正电子时产生的粒子的总质量（W）是多少？可能会产生什么介子？

50。 在满能量下，直径为2.00千米的费米实验室同步加速器中的质子以几乎光速传播，因为它们的能量约为其剩余质量能量的1000倍。

(a) 质子完成一次旅行需要多长时间？

(b) 它每秒会穿过目标区域多少次？

51。 假设在粒子探测器中\(\displaystyle W^−\)创建的可以存活\(\displaystyle 5.00×10^{−25}s\)。如果它以0.900c的速度行驶，它在这段时间内会移动多远？（请注意，时间比给定的\(\displaystyle W^−\)寿命长，这可能是由于衰减或时间膨胀的统计性质造成的。）

52。 如果在 0.100 摄氏度的气泡室中\(\displaystyle π^+\)行驶并存活，它会在气泡室中留下多长度的轨道\(\displaystyle 2.60×10^{−8}s\)？（移动速度更快或寿命更长的人可能会在腐烂之前逃离探测器。）

53。 3.20 千米长的 SLAC 会产生一束 50.0 GeV 的电子束。如果有 15,000 个加速管，它们之间的间隙必须有多大的平均电压才能获得这种能量？

11.5 标准模型

54。 使用海森堡不确定性原理，如果该力是通过交换 Z 玻色子产生的，则确定弱力的范围。

55。 使用海森堡不确定性原理来估计涉及引力子的弱核衰变的范围。

56。 (a) 以下衰变由电弱力介导:\(\displaystyle p→n+e^++\nu_e\). 绘制衰变的费曼图。

(b) 以下散射由电弱力介导:\(\displaystyle \nu_e+e^−→\nu_e+e^−\). 绘制散射的费曼图。

57。 假设动量守恒，在反应中，中性离子在静止时衰变所产生的每条\(\displaystyle γ\)射线的能量是\(\displaystyle π^0→γ+γ\)多少？

58。 在 SLAC 产生的 50 GeV 电子的波长是多少？这让人们了解了它可以探测的细节的极限。

59。 负介子的主要衰减模式为\(\displaystyle π^−→μ^−+\bar{\nu_μ}\).

(a) 这次衰变中以兆电子伏为单位释放的能量是多少？

(b) 使用动量守恒法，假设衰变产物在衰变时\(\displaystyle π^−\)处于静止状态，每种衰变产物会获得多少能量？你可能会假设 muon antineutrino 是无质量的\(\displaystyle p=E/c\)，有动量，就像光子一样。

60。 假设你正在设计质子衰变实验，你可以在水箱中检测到 50% 的质子衰变。

(a) 假设寿命为\(\displaystyle 10^{31}\) y，你需要多少千克水才能看到每月一次腐烂？

(b) 这是多少立方米的水？

11.6 宇宙大爆炸

61。 如果遥远星系的速度为0.99 c，那么该星系与地球观测者的距离是多少？

62。 星系与太阳系的距离为 10 Mpc。

(a) 银河系的衰退速度是多少？

(b) 来自这个星系的星光是多少（也就是说，它的 z 值是多少）？

63。 如果一个星系离我们有 153 Mpc 的距离，我们预计它会移动多快，朝哪个方向移动？

64。 平均而言，以光速的\(\displaystyle 2.0%\)百分比离开我们的星系距离有多远？

65。 我们的太阳系绕银河系的中心运行。假设圆形轨道半径为 30,000 ly，轨道速度为 250 km/s，那么一圈需要多少年？请注意，这是近似值，假设速度恒定，轨道为环形轨道，但它代表了我们的系统和局部恒星绕银河系旋转一圈的时间。

66。 (a) 在已知宇宙边缘附近，距离大约 10 Gly 的星系相对于我们的大概速度是多少？

(b) 这是光速的多少？请注意，我们已经观察到星系在大于 0.9 摄氏度的温度下从我们身边移动。

67。 (a) 根据哈勃常数的平均值计算宇宙的大概年龄,\(\displaystyle H_0=20km/s⋅Mly\). 为此，请计算以 20 km/s 的恒定膨胀速率行驶 0.307 Mpc 所需的时间。

(b) 如果以某种方式发生加速，宇宙的实际年龄会大于还是小于这里发现的年龄？解释一下。

68。 仙女座星系是最近的大星系，肉眼可以看见。估计它相对于太阳的亮度，假设它的亮度\(\displaystyle 10^{12}\)乘以太阳的亮度并且距离太阳0.613 Mpc。

69。 证明一颗恒星在圆形轨道上绕其星系运行的速度与其轨道半径的平方根成反比，假设其轨道内恒星的质量就像银河系中心的单个质量一样。你可以使用上一章中的方程来支持你的结论，但你必须证明其用法是合理的，并定义所有使用的术语。

其他问题

70。 实验结果表明，μ子会衰变为电子和光子。这怎么可能？

71。 以下每种反应都缺少一个粒子。找出每次反应中缺失的颗粒。

(a)\(\displaystyle p+\bar{p}→n+?\)

(b)\(\displaystyle p+p→p+Λ^0+?\)

(c)\(\displaystyle π^{−}+p→\sum{}^−+?\)

(d)\(\displaystyle K^−+n→Λ^0+?\)

(e)\(\displaystyle τ^+→e^++\nu_e+?\)

(f)\(\displaystyle \bar{\nu_e}+p→n+?\)

72。 由于欧洲核子研究组织大型强子对撞机中的同步加速器辐射造成的能量损失，在绕主环的每次旋转中，每个质子的能量仅增加5.00兆电子伏。如果注入的初始能量为 8.00 GeV，则产生 7.00-TeV（7000 GeV）质子需要多少转？

73。 质子和反质子正面碰撞，各自的动能为7.00 TeV（例如在欧洲核子研究组织的大型强子对撞机中）。考虑到两个质量的毁灭，有多少碰撞能量可用？（请注意，这并不明显高于极其相对论的动能。）

74。 当电子和正电子在 SLAC 设施碰撞时，它们各自具有 50.0-GeV 的动能。考虑到歼灭能量，可用的总碰撞能量是多少？请注意，歼灭能量微不足道，因为电子是高度相对论的。

75。 恒星的核心在超新星期间崩溃，形成中子星。核心的角动量是保守的，因此中子星会快速旋转。如果初始核心半径为\(\displaystyle 5.0×10^5km\)并且它崩溃到10.0 km，则找出中子星的角速度（以每秒转数为单位），因为中子星的角速度最初为每 30.0 天 1 转。

76。 使用前一个问题的解决方案，找出旋转动能的增加，因为核心的质量是我们太阳的1.3倍。动能的增加从何而来？

77。 (a) 哪个哈勃常数对应于\(\displaystyle 10^{10}\) y 宇宙的大致年龄？要获得近似值，请假设膨胀率恒定，然后计算两个星系在 y 时间内必须分开才能被 1 Ml\(\displaystyle 10^{10}\) y（当前平均银河分离）分开的速度。

(b) 同样，哈勃常数对应于大约\(\displaystyle 2×10^{10}\)几年的宇宙？

挑战问题

78。 电子和正电子在圆形加速器中碰撞。推导出粒子质心能量的表达式。

79。 宇宙射线辐射的强度随着能量的增加而迅速降低，但偶尔会有高能的宇宙射线，它们通过撞击大气中的原子核而产生的所有粒子产生一阵辐射。假设一个能量为的宇宙射线粒子将其能量\(\displaystyle 10^{10}GeV\)转换为质量平均值的粒子\(\displaystyle 200MeV/c^2\)。

(a) 产生了多少粒子？

(b) 如果颗粒降落在某个\(\displaystyle 1.00-km^2\)区域，则每平方米有多少颗粒？

80。 (a) 计算费米实验室产生的1.00-TEV质子的相对论量\(\displaystyle γ=1\frac{1}{\sqrt{1−v^2/c^2}}\)。

(b) 如果这样的质子\(\displaystyle π^+\)产生了速度相同的质子，它在实验室中的寿命会持续多久？

81。 为了研究强力，计划使用一种能产生二次K介子束从原子核散射的加速器，要求它们的动能为500兆电子伏。

(a) 这些粒子的相对论量\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\)是多少？

(b) 它们在实验室中的平均寿命会有多长？

82。 在超新星中，大量产生中微子。它们是从麦哲伦云中的1987A超新星中发现的，麦哲伦云距离地球约12万光年（相对靠近我们的银河系）。如果中微子有质量，它们就无法以光速传播，但是如果它们的质量很小，它们的速度将几乎等于光的速度。

(a) 假设具有\(\displaystyle 7-eV/c^2\)质量的中微子的动能为 700 keV。找到它的相对论量\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\)。

(b) 如果中微子与光子同时离开 1987A 的超新星并且两者都进入地球，那么光子会早多久到达？这不是一个很大的时差，因为不可能知道哪个中微子还剩下哪个光子，而且中微子探测器的效率很差。因此，在超新星变亮后的几个小时内就观测到中微子这一事实只对中微子的质量设定了上限。（提示：你可能需要使用系列扩展才能为中微子找到 v，因为它\(\displaystyle γ\)太大了。）

83。 假设太阳绕银河系中心绕着圆形轨道，使用以下信息计算其轨道速度：银河系的质量等于太阳（或）的单质量\(\displaystyle 1.5×10^{11}\)乘以 30,000 ly 之外的太阳（或\(\displaystyle 3×10^{41}kg\)）。

84。 (a) 假设仙女座星系的总质量是我们太阳的质量并且像0.613 Mpc以外的单一质量一样起作用\(\displaystyle 10^{13}\)，那么由于仙女座星系，70公斤的人受到的重力大约是多少？

(b) 这种力量与人体重的比例是多少？请注意，仙女座是最近的大星系。

85。 (a) 粒子及其反粒子相对于观察者处于静止状态并消灭（完全摧毁两个质量），产生两条能量相等的\(\displaystyle γ\)射线。如果寻找质子\(\displaystyle γ\)-反质子毁灭的证据，你会寻找什么典型的射线能量？（很少观察到这种辐射这一事实证明宇宙中几乎没有反物质。）

(b) 这与与电子正电子歼灭相关的0.511兆电子伏能量相比如何？

86。 CMBR 的峰值强度出现在 1.1 mm 的波长处。

(a) 1.1 mm 光子的能量（以 eV 为单位）是多少？

(b) 深空中每个大粒子大约有\(\displaystyle 10^9\)光子。计算\(\displaystyle 10^9\)此类光子的能量。

(d) 这是否意味着空间被 “物质主导”？简要解释一下。

87。 (a) 使用海森堡不确定性原理计算相应时间间隔内的能量不确定性\(\displaystyle 10^{−43}s\)。

(b) 将这种能量与\(\displaystyle 10^{19}GeV\)力量统一能量进行比较，并讨论它们为何相似。