1.E：光的本质（练习）

概念性问题

1.1 光的传播

1。 在什么条件下光可以像射线一样建模？ 像波浪一样？

2。 为什么折射率总是大于或等于 1？

3。 闪电发出的光在发出声音之前闪烁的事实是否证明光速非常大，还是仅仅证明光速大于声速？ 讨论如何使用此效果来估算光速。

4。 猜测哪种物理过程可能导致光在介质中的传播速度比在真空中传播得更慢。

1.2 反思定律

5。 使用反射定律，解释粉末如何去除人鼻子上的光泽。 光学效应的名字是什么？

1.3 折射

6。 本章描述了粗糙表面反射产生的扩散。 光也可以通过折射来扩散。 描述这种情况在特定情况下是如何发生的，例如光与碎冰相互作用。

7。 当光线从空气流向水时，它会朝向或远离垂直线的方向改变吗？ 水到玻璃杯？ 玻璃到空气？

8。 解释一下为什么水中物体的深度总是比实际要浅一些？

9。 解释为什么一个人在游泳池里涉水时双腿显得很短。 用一张射线图来证明你的解释是合理的，该射线图显示了射线从脚到出水的观察者的眼睛的路径。

10。 解释为什么部分浸入水中的桨会出现弯曲现象。

1.4 全内部反射

11。 镶有无色宝石的戒指掉入水中。 宝石在浸入水中时会变得隐身。 可以是钻石吗？ 解释一下。

12。 最常见的幻影类型是一种错觉，即来自遥远物体的光线会被实际上不存在的水池反射。 通常在沙漠中观察到幻影，那时地面附近有一层热空气。 鉴于温度较高时空气的空气折射率较低，请解释如何形成海市蜃楼。

13。 如何使用全内反射来估计介质的折射率？

1.5 分散

14。 全内反射有可能在彩虹中起作用吗？ 用折射指数和角度来解释，也许可以参考下图所示。 我们当中有些人已经看到了双彩虹的形成；物理上有可能观察到三重彩虹吗？ 一张双彩虹的照片。

15。 高质量的钻石可能非常透明和无色，几乎没有吸收力，可以透射所有可见波长。 解释一下它在白光照亮时如何闪烁着鲜艳的色彩。

1.6 惠更斯原理

16。 波浪效果如何取决于与波浪相互作用的物体的大小？ 例如，为什么声音在建筑物的拐角处弯曲，而光线却没有？

17。 惠更斯的原理是否适用于所有类型的波浪？

18。 如果观察到某种现象的衍射，则证明该现象是波浪。 反过来是否成立？ 也就是说，如果没有观察到衍射，这是否意味着这种现象不是波浪？

1.7 两极化

19。 空气中的声波可以偏振吗？ 解释一下。

20。 没有光线通过两个具有垂直轴的完美偏振滤光片。 但是，如果在原来的两个偏振滤光片之间放置第三个偏振滤光片，则一些光线可能会通过。 这是为什么？ 在什么情况下，大部分光线会通过？

21。 解释光携带的能量通过两个交叉的偏振滤光片会变暗，会发生什么情况。

22。 当散射光的粒子远小于其波长时，散射量与之成正比\(\displaystyle \frac{1}{λ}\)。 这是否意味着小散射\(\displaystyle λ\)比大散射多\(\displaystyle λ\)？ 这与天空是蓝色的事实有何关系？

23。 使用前面问题中给出的信息，解释为什么日落是红色的。

24。 当光线从光滑的表面以布鲁斯特的角度反射时，它会平行于表面\(\displaystyle 100%\)偏振。 部分光线将被折射到表面。 描述您将如何进行实验以确定折射光的偏振。 你预计两极分化会走向什么方向？你会期望它会走向什么方向\(\displaystyle 100%\)？

25。 如果你躺在沙滩上看水，头稍微向侧身倾斜，那么你的偏光太阳镜效果不佳。 为什么不呢？

问题

1.1 光的传播

26。 水中的光速是多少？ 在甘油中？

27。 空气中的光速是多少？ 在皇冠玻璃里？

28。 计算光速所在介质的折射率\(\displaystyle 2.012×10^8m/s\)，并根据表1.1确定最有可能的物质。

29。 表1.1中的哪种物质是光速\(\displaystyle 2.290×10^8m/s\)？

30。 在中世纪，一颗小行星与月球发生了重大碰撞。 英格兰坎特伯雷大教堂的僧侣们将其描述为月球上和月球周围的红色光芒。 在小行星撞击\(\displaystyle 3.84×10^5km\)离月球多久之后，光会首先到达地球？

31。 一些计算机的组件通过具有折射率的光纤相互通信\(\displaystyle n=1.55\)。 信号通过这种光纤传输 0.200 m 需要多长时间（纳秒）？

32。 比较一下光在地球表面和外太空传播 1000 米所花费的时间。

33。 在一段时间内，光能在水下传播多远\(\displaystyle 1.50×10^{−6}s\)？

1.2 反思定律

34。 假设一个人站在镜子前，如下所示。 他的眼睛高出地板1.65米，头顶高0.13米。 找到最小的镜子顶部和底部在地板上方的高度，在镜子里他可以看到头顶和脚的顶部。 这个距离与男人的身高有何关系？

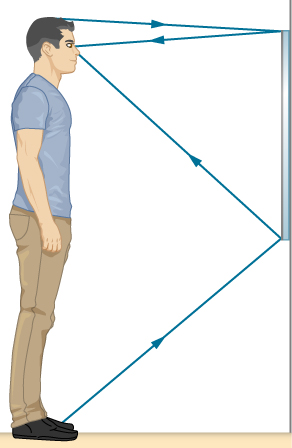
这幅画描绘了一个男人站在镜子前看着自己的形象。 镜子大约是男人的一半高，镜子的顶部在他的眼睛上方，但低于他的头顶。 他脚下的光线到达镜子底部，反射到他的眼睛。 来自他头顶的光线到达镜子的顶部，反射到他的眼睛。

35。 显示当光线从两个以直角相交的反射镜反射时，传出的光线与入射的光线平行，如下图所示。

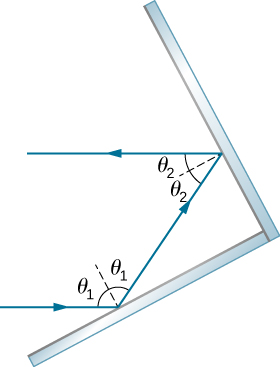
两面镜子以直角相遇。 入射的光线以 theta 与法线成一定角度照射一面镜子，以与 theta 相同的角度反射到法线的另一侧，然后以 theta 2 的角度击中另一面镜子，然后以与法线另一侧的 theta two 相同的角度反射，这样传出的射线与入射的射线平行。

36。 在月球表面，月球宇航员放置了一个角反射镜，激光束定期从上面反射出来。 到月球的距离是根据往返时间计算得出的。 需要多少百分比的校正才能解释由于地球大气中光线减速而导致的时间延迟？ 假设到月球的距离很精确\(\displaystyle 3.84×10^8m\)，地球的大气层（密度随海拔高度而变化）相当于一个厚度为30.0 km且折射率恒定的层\(\displaystyle n=1.000293\)。

37。 平面反射镜既不会聚也不会发散。 为了证明这一点，可以考虑两条来自同一点并以一定角度发散的射线\(\displaystyle θ\)（见下文）。 表明在撞击飞机镜子后，它们的方向之间的角度仍然存在\(\displaystyle θ\)。

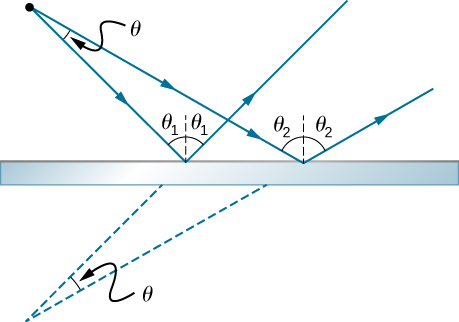
从某个点发散的光线成一定角度 theta，在两个不同的地方入射到镜子上，它们的反射光线会发散。 一条射线以与法线相差一的角度击中，并以相同的角度反射到法线的另一侧。 另一条射线以距离法线二的更大角度击中，并以相同的角度在法线的另一侧反射 theta two。 当反射光线从反射点向后延伸时，它们在镜子后面的某个点相遇，其角度与离开光源的角度相同。

1.3 折射

除非另有说明，否则对于问题 1 到 10，玻璃和水的折射指数应分别设为 1.50 和 1.333。

38。 空气中的光束在玻璃板表\(\displaystyle 35°\)面的入射角为。 反射和折射的角度是多少？

39。 空气中的光束入射到池塘表面，相对于池塘表面形成\(\displaystyle 20°\) 20°的角度。 反射和折射的角度是多少？

40。 当光线从水穿过玻璃时，它会以\(\displaystyle 30°\)相对于界面法线的角度出现。 它的入射角是多少？

41。 浸入水中的铅笔手电筒以入射角向地表发出光束\(\displaystyle 30°\)。 空气中的折射角度是多少？

42。 从水体表面下方观察时，来自太阳的光线会与垂直方向成\(\displaystyle 30°\)一定角度。 太阳在地平线上方的哪个角度？

43。 当光束进入矩形塑料块\(\displaystyle 22°\)时，其在空气中的路径从入射角变为折射角。\(\displaystyle 35°\) 塑料的折射率是多少？

44。 在游泳池里训练的水肺潜水员看着他的教练，如下所示。 在射线进入时，来自教练脸部的光线与垂直于水的光线会形成什么角度？ 水中的射线和垂直于水的射线之间的角度为\(\displaystyle 25.0°\)。

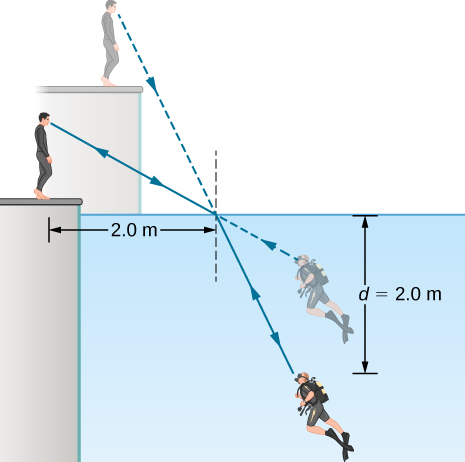
水肺潜水员和他的教练互相看着对方。 他们在直线推断到达眼睛的光线给出的位置互相看见。 在训练师看来，水肺潜水员的深度没有实际那么深，而对潜水员来说，训练师看起来比实际要高。 在训练师看来，水肺潜水员的脚似乎在两点零米的深度。 来自训练器的入射射线在距离训练器零米的两点水平距离处撞击水面。 潜水员的头部垂直距离为 d，等于水面以下零米处两点。

45。 (a) 使用前一问题中的信息，找出教师头部在水面之上的高度，注意你必须先计算入射角。

(b) 找到教练看到的潜水员头部在水下的表观深度。

1.4 全内部反射

46。 验证光从水流向空气的临界角度是否\(\displaystyle 48.6°\)如示例 1.4 末尾所述，即光在被空气包围的聚苯乙烯（一种塑料）管道中传播的临界角度。

47。 (a) 在示例 1.4 的末尾，有人说光从钻石到空气的临界角度为\(\displaystyle 24.4°\)。 验证一下。

(b) 光从锆石到空气的临界角度是多少？

48。 光纤使用覆盖有冠状玻璃的火石玻璃。 临界角度是多少？

49。 光在水中传播并从冰中反射出来，你能以什么最小角度获得完全的内部反射？

50。 假设您正在使用全内反射来制作高效的角反射镜。 如果外面有空气并且入射角为\(\displaystyle 45.0°\)，那么制作反射镜的材料的最小折射率必须是多少？

51。 您可以通过确定物质的临界角度来确定其折射率。

(a) 浸入水中\(\displaystyle 68.4°\)时具有临界角的物质的折射率是多少？ 根据表1.1，该物质是什么？

(b) 这种物质在空气中的临界角是多少？

52。 一束光线在未知液体的表面下发射，上面有空气，会经历完全的内部反射，如下所示。 液体的折射率及其可能的识别率是多少？

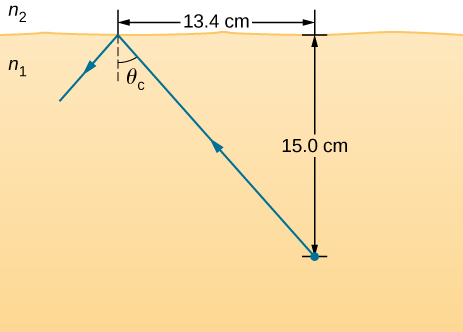
光线从放置在介质 n 1 中的物体传出，该物体位于水平界面下方 15.0 厘米处，介质 n 2。 这条光线完全在内部反射，以 theta c 作为临界角度。 物体和入射点之间的水平距离为 13.4 厘米。

53。 光线通常落在玻璃棱镜的垂直表面上（\(\displaystyle n=1.50\)如下所示）。

(a) 光线完全反射到倾斜面的最大值是多少？\(\displaystyle ϕ\)

(b) 如果棱镜浸入水中，则重复 (a) 部分的计算。

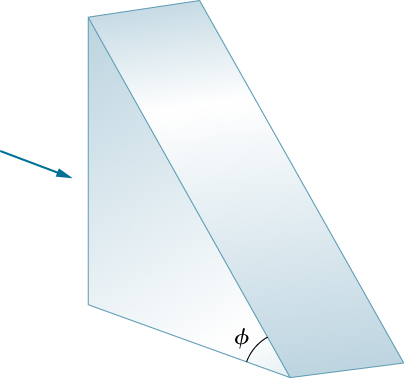
直角三角棱镜具有水平底座和垂直边。 三角形的斜边与水平底部形成了 phi 的角度。 水平光线通常入射到棱镜的垂直表面。

1.5 分散

54。 (a) 根据表 1.2，钻石中红光与紫光的速度之比是多少？

(b) 聚苯乙烯中的这个比例是多少？

(c) 哪个更分散？

55。 一束白光从空气进入水中，入射角为\(\displaystyle 75.0°\)。 光的红色（660 nm）和紫色（410 nm）部分在什么角度折射？

56。 在被空气包围的钻石中，红光（660 nm）和紫光（410 nm）的临界角度有何不同？

57。 (a) 包含黄色（580 nm）和绿色（550 nm）波长的窄光束从聚苯乙烯流向空气，以入\(\displaystyle 30.0°\)射角撞击表面。 当颜色出现时，它们之间的角度是多少？

(b) 它们必须走多远才能相隔1.00毫米？

58。 含有橙色（610 nm）和紫罗兰（410 nm）波长的平行光束从熔融石英流向水，以入\(\displaystyle 60.0°\)射角撞击它们之间的表面。 水中两种颜色之间的角度是多少？

59。 一束 610 纳米的光线从空气进入熔融石英，入射角为\(\displaystyle 55.0°\)。 470 nm 的光必须以什么入射角度进入火石玻璃才能获得相同的折射角度？

60。 包含红色（660 nm）和蓝色（470 nm）波长的窄光束从空气中穿过一块 1.00 厘米厚的扁平冠玻璃，然后再次返回空中。 光束以入\(\displaystyle 30.0°\)射角击中。

(a) 这两种颜色在什么角度出现？

(b) 当红色和蓝色出现时，它们之间的距离是多少？

61。 一束狭窄的白光以入\(\displaystyle 45.0°\)射角进入由皇冠玻璃制成的棱镜，如下所示。 光的红色（660 nm）和紫色（410 nm）成分在什么角度从棱镜中冒出来？\(\displaystyle θ_R\)\(\displaystyle θ_V\)

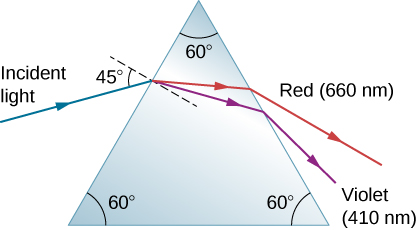
入射角等于法线45度的蓝色入射光线落在等边三角棱镜上，该棱镜的角均等于60度。 在第一个表面，光线折射并分裂成红色和紫色射线。 这些光线击中第二个表面并从棱镜中冒出来。 660 纳米的红光的弯曲度小于 410 纳米的紫光。

1.7 两极化

62。 偏振光的方向和偏振滤光片的轴线之间需要多大的角度才能将其强度减半？

63。 两个偏振滤光片的轴线之间的角度为\(\displaystyle 45.0°\)。 第二个滤镜会降低通过第一个滤镜的光的强度多少？

64。 两张偏振片\(\displaystyle P_1\)放在一起，它们的传输轴彼此成一定角度\(\displaystyle θ\)。\(\displaystyle P_2\) \(\displaystyle θ\)当只有\(\displaystyle 25%\)最大透射光强度通过它们时会怎样？

65。 假设在前面的问题中，入射的光\(\displaystyle P_1\)是非极化的。 在确定的值下\(\displaystyle θ\)，入射光中有多少部分通过组合？

66。 如果你有完全偏振的强度光\(\displaystyle 150W/m^2\)，那么经过偏振滤光片后，它的强度会是多少，其轴线与光的偏振方向成\(\displaystyle 89.0°\)一定角度？

67。 偏振滤光片的轴线需要与强度偏振光的方向形成什么角度\(\displaystyle 1.00kW/m^2\)才能将强度降低到\(\displaystyle 10.0W/m^2\)？

68。 在示例 1.7 的末尾，有人指出，通过偏振滤光片，偏振光\(\displaystyle 90.0%\)的轴线与偏振方向成一定角度，从而将偏振光的强度降低\(\displaystyle 18.4°\)到其原始值。 验证此陈述。

69。 表明，如果你有三个偏振滤镜，其中\(\displaystyle 45.0°\)第二个与第一个偏振滤镜成一定角度，第三个偏振滤镜与第一个偏振滤镜成一定角度，则第一个偏振滤镜通过的光强度将减小到\(\displaystyle 25.0%\)其值。\(\displaystyle 90.0°\) （这与只有第一个和第三个形成鲜明对比，后者会将强度降低到零，因此将第二个放在它们之间会增加透射光的强度。）

70。 将三张偏振片放置在一起，使得第二张偏振片的传输轴定向\(\displaystyle 25.0°\)到第一张片的轴线，而第三张偏振片的传输轴定向于\(\displaystyle 40.0°\)（从同样的意义上讲）与第一张片的轴线。 入射非极化光束的强度中有多少部分是由这种组合传输的？

71。 为了使线性偏振光束的偏振轴旋转\(\displaystyle 90.0°\)，学生将纸张\(\displaystyle P_1\)和\(\displaystyle P_2\)透射轴分别放在光束的偏振轴上\(\displaystyle 45.0°\)。\(\displaystyle 90.0°\)

(a) 入射光中有多少部分通过\(\displaystyle P_1\)，以及

(b) 通过组合？

(c) 对 (b) 部分重复计算，分别计算\(\displaystyle 30.0°\)和\(\displaystyle 90.0°\)的传输轴角度。

72。 研究发现，当水中传播的光线落在塑料块上时，布鲁斯特的角度是\(\displaystyle 50.0°\)。 塑料的折射率是多少？

73。 钻石反射的光在什么角度会完全偏振？

74。 布鲁斯特对皇冠玻璃反射出的光线在水中传播的角度是多少？

75。 水肺潜水员看到从水面反射的光线。 这种光将在什么角度完全偏振？

其他问题

76。 根据他的测量，罗默估计，光的传播距离等于地球绕太阳轨道直径的距离需要22分钟。

(a) 将该估计值与已知的地球轨道直径一起使用，得出光速的粗略值。

(b) 光线实际上需要 16.5 分钟才能传播这个距离。 使用这段时间来计算光速。

77。 Cornu 使用直径为 4.00 厘米、包含 180 颗齿的轮子对 Fizeau 进行了光速测量。 从车轮到镜子的距离为 22.9 km。 假设他准确地测量了光速，那么车轮的角速度是多少？

78。 假设你有一种未知的透明物质浸入水中，你想通过找到它的折射率来识别它。 你安排一束光束以一定角度进入它\(\displaystyle 45.0°\)，然后观察折射角度\(\displaystyle 40.3°\)。 该物质的折射率及其可能的身份是多少？

79。 下图显示的是从空气穿过皇冠玻璃进入水中的光线，例如进入鱼缸。 假设入射角为\(\displaystyle 40.0°\). 且玻璃厚度为 1.00 厘米\(\displaystyle (Δx)\)，计算光线被玻璃移位的量。

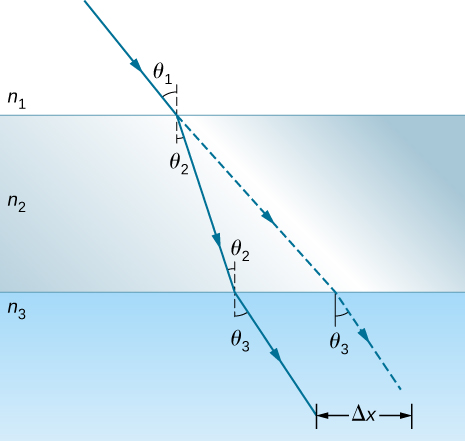
该图说明了光线从介质传播到中间介质\(\displaystyle n_1\)时发生的折射\(\displaystyle n_2\)。\(\displaystyle n_3\) 入射射线形成一个角度，在\(\displaystyle n_1\)和之间的\(\displaystyle θ_1\)交界处的入射点处绘制一个垂直线\(\displaystyle n_2\)。 进入的光线向垂直线\(\displaystyle n_2\)弯曲，使其在\(\displaystyle n_2\)侧面成一定角度\(\displaystyle θ_2\)。 射线到达介于该界面入射点处绘制的\(\displaystyle θ_2\)垂直线之间的\(\displaystyle n_2\)界面和垂直角度，透射的射线从垂直线弯曲，使\(\displaystyle n_3\)侧面与垂直线成三的角度。\(\displaystyle n_3\) 原始入射射线的直线外推显示为虚线。 这条线平行于第三个介质中的折射光线\(\displaystyle n_3\)，并且与折射光线偏移了一段距离 delta x 的距离。 外推的射线与折射光线在介质中\(\displaystyle n_3\)与垂直方向的角度是相同的 theta 3。

80。 考虑到前面的问题，证明\(\displaystyle θ_3\)这与不存在第二种媒介时的情况相同。

81。 当从水中反射时，皇冠玻璃内部的光会以什么角度完全偏振，就像在鱼缸里一样？

82。 \(\displaystyle 55.6°\)从窗户反射的光线完全偏振。 窗户的折射率是多少？它可能由什么物质构成？

83。 (a) 戒指\(\displaystyle 62.5°\)中宝石反射的光线完全偏振。 宝石可以是钻石吗？

(b) 如果宝石在水中，光线会以什么角度完全偏振？

84。 如果布鲁斯特的光从两种物质之间的界面顶部反射的角度\(\displaystyle θ_b\)是布鲁斯特的角度，\(\displaystyle θ'_b\)也是布鲁斯特从下方反射光的角度，那就证明这一点\(\displaystyle θ_b+θ'_b=90.0°\)。

85。 不合理的结果假设光从水传播到另一种物质，入射角\(\displaystyle 10.0°\)和折射角为\(\displaystyle 14.9°\)。

(a) 另一种物质的折射率是多少？

(b) 这个结果有什么不合理之处？

(c) 哪些假设不合理或不一致？

86。 不合理的结果从水流向宝石的光线以一定角度撞击表面，折射角度为\(\displaystyle 15.2°\)。\(\displaystyle 80.0°\)

(a) 宝石中的光速是多少？

(b) 这个结果有什么不合理之处？

(c) 哪些假设不合理或不一致？

87。 如果偏振滤光片将偏振光的强度降低到\(\displaystyle 50.0%\)其原始值，则电场和磁场会减少多少？

88。 假设你戴上了两副偏光太阳镜，它们的轴线成一定角度\(\displaystyle 15.0°\)。 与一副太阳镜相比，光线在你的眼睛中沉积一定量的能量需要多长时间？ 假设镜片除了偏光特性之外都是透明的。

89。 (a) 在阳光强度较高的日子\(\displaystyle 1.00kW/m^2\)，直径为0.200 m的圆形透镜将光聚焦在黑色烧杯中的水上。 两片偏光塑料片放置在镜头前面，它们的轴线成一定角度\(\displaystyle 20.0°\)。 假设阳光是非极化的，偏光镜是\(\displaystyle 100%\)有效的，那么假设它\(\displaystyle 80.0%\)被吸收了\(\displaystyle °C/s\)，水的初始加热速率是多少？ 铝制烧杯的质量为 30.0 克，含有 250 克水。

(b) 偏振滤光片会变热吗？ 解释一下。

挑战问题

90。 用激光上演的灯光秀使用移动的镜子摆动光束并创造出丰富多彩的效果。 显示当镜子旋转一定角度\(\displaystyle 2θ\)时，从镜子反射的光线会改变方向\(\displaystyle θ\)。

91。 假设阳光在日出和日落时分进入地球大气层，也就是说，以\(\displaystyle 90.0°\)入射角度。 假设几乎空旷的空间和大气之间的边界是突然的，计算阳光的折射角度。 这延长了日出和日落时太阳出现在地平线之上的时间。 现在构造一个问题，在该问题中，您可以确定不同大气模型的折射角度，例如不同密度的各个层。 教师不妨指导您考虑的复杂程度以及折射率如何随空气密度变化。

92。 进入被空气包围的光纤的光线首先被折射，然后反射，如下所示。 表明，如果纤维由冠状玻璃制成，则任何入射光线都将完全在内部反射。

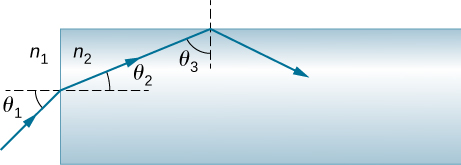
该图显示了来自矩形材料块左表面\(\displaystyle n_1\)并入射到其左面的光线\(\displaystyle n_2\)。 射线以入射角入射\(\displaystyle θ_1\)，相对于射线进入的表面的法线进行测量。 同样\(\displaystyle θ_2\)，折射角度是相对于表面法线的。 折射的光线落在方块的上表面上，并以入射角的\(\displaystyle θ_3\)形式在内部完全反射。

93。 光线以入射角落在棱镜的左面（见下文），新兴光束\(\displaystyle θ\)在右面有一个折射角度。\(\displaystyle θ\) 表明玻璃棱镜的折射率 n 由\(\displaystyle n=\frac{sin\frac{1}{2}(α+ϕ)}{sin\frac{1}{2}ϕ}\)棱镜的顶角和\(\displaystyle α\)光束偏离的角度给出。\(\displaystyle ϕ\) 如果\(\displaystyle α=37.0°\)和棱镜的基角都是\(\displaystyle 50.0°\)，那么 n 是什么？

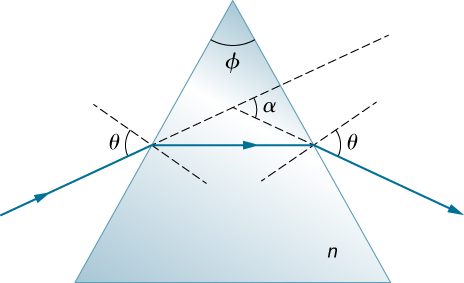
光线落在三角棱镜的左面，该棱镜的上顶角为 phi，折射率为 n。光线相对于左面法线的入射角为 theta。 光线在棱镜中折射。 折射的光线是水平的，平行于棱镜的底部。 折射的光线到达棱镜的右面，当它从棱镜出来时会折射。 新出现的射线形成一个 theta 的角度，法线向右面。

94。 如果上一个问题\(\displaystyle ϕ\)中的顶角是\(\displaystyle 20.0°\)和\(\displaystyle n=1.50\)，那么的值是多\(\displaystyle α\)少？

95。 入射在偏振片\(\displaystyle P_1\)上的光线\(\displaystyle 30.0°\)相对于的透射轴线呈线性偏振\(\displaystyle P_1\)。 片材\(\displaystyle P_2\)的放置使其轴线平行于入射光的偏振轴，也就是说，\(\displaystyle 30.0°\)相对于入射光的偏振轴也是如此\(\displaystyle P_1\)。

(a) 入射光中有多少部分通过\(\displaystyle P_1\)？

(b) 入射光中有多少部分是通过组合的？

(c) 通过旋转\(\displaystyle P_2\)，可获得最大透射强度。 这个最大强度\(\displaystyle 30.0°\)与透射光强度的比率\(\displaystyle P_2\)是\(\displaystyle P_1\)多少？

96。 证明如果 I 是两个偏振滤光片传输的光的强度，轴成一定角度，\(\displaystyle θ\)并且\(\displaystyle I'\)是轴成一定角度时的强度\(\displaystyle 90.0°−θ\)\(\displaystyle I+I'=I_0\)，那么就是原始强度。 （提示：使用三角恒\(\displaystyle cos90.0°−θ=sinθ\)等式和\(\displaystyle cos^2θ+sin^2θ=1\)。）