需求和供应曲线都显示了价格与需求或供应单位数量之间的关系。 价格弹性 需求的价格弹性 需求 数量的百分比变化除以价格的百分比变化。 供应的价格弹性等于供应
弹性可以有效地分为三大类:弹性、非弹性和单一性。 弹性需求 弹性供应 非弹性需求 非弹性供应 示,统一弹性
如果。。 那么。。 而且它被称为。。
\(\%\,change\,in\,quantity\,\gt\,\%\,change\,in\,price\) \(\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\,\gt\,1\) 弹性
\(\%\,change\,in\,quantity\,=\,\%\,change\,in\,price\) \(\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\,=\,1\) 单一制
\(\%\,change\,in\,quantity\,\lt\,\%\,change\,in\,price\) \(\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\,\lt\,1\) 无弹性
表 1:弹性、非弹性和单一性:三种弹性案例
注意
在我们深入探讨弹性的本质之前,请阅读这篇关于超级碗弹性和门票价格的文章。
为了计算弹性,经济学家没有使用数量和价格的简单百分比变化,而是使用数量和价格的平均百分比变化。 这称为弹性中点法,用以下方程表示:
\[\%\,change\,in\,quantity\,=\,\dfrac{Q_2-Q_1}{(Q_2+Q_1)/2}\,\times\,100\]
\[\%\,change\,in\,price\,=\,\dfrac{P_2-P_1}{(P_2+P_1)/2}\,\times\,100\]
is Midpoint 方法 的优势在于,无论价格上涨还是下降,都可以在两个价格点之间获得相同的弹性。 这是因为公式在两种情况下使用相同的基数。
计算需求的价格弹性
让我们计算图 1 所示点 A 和 B 之间以及点 G 和 H 之间的弹性。
计算需求的价格弹性
图 1:需求的价格弹性是通过数量变化百分比除以价格变动百分比计算得出的。 首先,当价格从B点的70美元降至A点的60美元时,应用该公式来计算弹性:
\[\%\,change\,in\,quantity\,=\,\dfrac{3000-2800}{(3000+2800)/2}\times100\]
\[=\,\dfrac{200}{2900}\times100\]
\[=\,6.9\]
\[\%\,change\,in\,price\,=\,\dfrac{60-70}{(60+70)/2}\times100\]
\[ =\,\dfrac{-10}{65}\times100\]
\[=\,-15.4\]
\[Price\,Elasticity\,of\,Demand=\,\dfrac{6.9\%}{-15.4%}\]
\[=0.45\]
因此,这两个点之间的需求弹性为\(\dfrac{6.9\%}{-15.4%}\) 0.45,小于1,这表明需求在此间隔内没有弹性。 需求的价格弹性总是 负的,因为需求的价格和数量总是朝相反的方向移动(在需求曲线上)。 按照惯例,我们总是将弹性说成正数。 因此,从数学上讲,我们取结果的绝对值。 从现在开始,我们将忽略这个细节,同时记得将弹性解释为正数。
这意味着,沿着B点和A点之间的需求曲线,如果价格变动1%,则需求量将变化0.45%。 价格的变化将导致需求数量的百分比变化较小。 例如,价格上涨 10%将仅导致需求量减少 4.5%。 价格下降 10%将导致需求量仅增加 4.5%。 需求的价格弹性是负数,表示需求曲线向下倾斜,但被视为绝对值。 以下 Work It Out 功能将引导您计算需求的价格弹性。
注意:寻找需求的价格弹性
使用图 1 中的数据计算需求的价格弹性,将价格从 G 提高到 H。弹性是增加还是减少了?
第 1 步。 我们知道:
\[Price\,Elasticity\,of\,Demand=\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\]
第 2 步。 从中点公式 中我们知道:
\[\%\,change\,in\,quantity\,=\,\dfrac{Q_2-Q_1}{(Q_2+Q_1)/2}\,\times\,100\]
\[\%\,change\,in\,price\,=\,\dfrac{P_2-P_1}{(P_2+P_1)/2}\,\times\,100\]
第 3 步。 因此,我们可以在每个方程中使用图中提供的值:
\[\%\,change\,in\,quantity\,=\,\dfrac{1600-1800}{(1600+1800)/2}\,\times\,100\]
\[=\,\dfrac{-200}{1700}\,\times\,100\]
\[=\,-11.76\]
\[\%\,change\,in\,price\,= \,\dfrac{130-120}{(130+120)/2}\,\times\,100\]
\[=\,\dfrac{10}{125}\,\times\,100\]
\[=\,8.0\]
第 4 步。 然后,这些值可用于确定需求的价格弹性:
\[Price\,Elasticity\,of\,Demand=\dfrac{ \%\,change\,in\,quantity }{ \%\,change\,in\,price}\]
\[=\dfrac{-11.76}{8}\]
\[=1.47\]
因此,需求弹性从G到H 1.47。 随着我们沿需求曲线 直线需求曲线的
计算供应的价格弹性
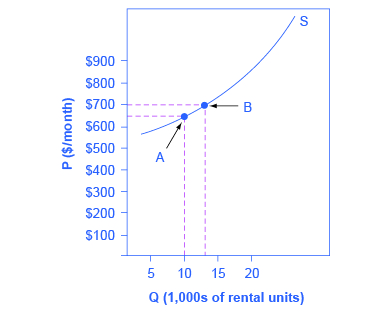
假设一套公寓的月租金为650美元,以该价格租用10,000套公寓,如图2所示。 当价格上涨到每月700美元时,将向市场供应13,000台。 公寓供应量增加了多少百分比? 价格敏感度是多少?
供应的价格弹性
图 2:供应的价格弹性是通过数量变化百分比除以价格变动百分比计算得出的。 使用中点法
\[\%\,change\,in\,quantity\,=\,\dfrac{13000-10000}{(13000+10000)/2}\,\times\,100\]
\[=\,\dfrac{3000}{11500}\,\times\,100\]
\[=\,26.1\]
\[\%\,change\,in\,price\,= \,\dfrac{\$700-\$600}{(\$700+\$600)/2}\,\times\,100\]
\[=\,\dfrac{50}{650}\,\times\,100\]
\[=\,7.69\]
\[Price\,Elasticity\,of\,Supply=\dfrac{26.1\%}{7.69\%}\]
\[=3.39\]
同样,与需求弹性一样,供应弹性不随任何单位而后。 弹性是一个百分比变化与另一个百分比变化的比率(仅此而已),被读为绝对值。 在这种情况下,价格上涨1%会导致供应量增加3.5%。 供应弹性大于一意味着供应数量的百分比变化将大于百分之一的价格变动。 如果你开始怀疑斜率的概念是否适合这个计算,请阅读下面的 Clear It Up 方框。
注意:弹性是斜率吗?
将供应或需求曲线的斜率与其弹性混淆是常见的错误。 斜率是沿曲线或上升/运行单位的变化率(y 在 x 变化中的变化)。 例如,在图 1 中,需求曲线上显示的每个点,价格下跌 10 美元,需求单位数量增加 200。 因此,整个需求曲线的斜率为 —10/200,并且没有变化。 但是,价格弹性沿曲线变化。 点 A 和 B 之间的弹性为 0.45,点 G 和 H 之间的弹性增加到 1.47。弹性是百分比 变化,它与斜率的计算方法不同,含义也不同。
当我们处于需求曲线的上端,价格高,需求量低时,需求量的微小变化,即使(比如)一个单位,按百分比计算,也是相当大的变化。 比如说,一美元的价格变化在百分比上将远不如需求曲线底部那么重要。 同样,在需求曲线的底部,需求量高时一个单位的变化百分比将很小。
因此,在需求曲线的一端,需求量有很大的百分比变化,而价格变化很小,弹性值会很高,或者需求将相对具有弹性。 即使价格变化相同,需求数量也发生相同变化,但在需求曲线的另一端,数量要高得多,价格要低得多,因此需求数量的百分比变化较小,价格的百分比变化要高得多。 这意味着在曲线的底部,我们在大分母上会有一个小分子,因此弹性测量值会低得多,或者没有弹性。
当我们沿着需求曲线移动时,数量和价格的值会上升或下降,这取决于我们的移动方向,因此(比如)1美元的价格差异或一个单位的数量差异的百分比也会发生变化,这意味着这些百分比的比率将发生变化。
关键概念和摘要
价格弹性衡量商品的需求或供应量对其价格变化的响应程度。 它的计算方法是需求(或供应)数量的百分比变化除以价格的百分比变化。 弹性可以描述为弹性(或反应非常灵敏)、单位弹性或非弹性(反应性不强)。 弹性需求或供应曲线表明,需求或供应的数量对价格变动的反应大于成比例。 非弹性需求或供应曲线是指给定的价格变化百分比将导致需求或供应数量的百分比变化较小的曲线。 统一弹性意味着给定的价格百分比变化会导致需求或供应数量的相同百分比变化。
词汇表
弹性需求
当需求弹性大于 1 时,表明需求或供应的数量对价格变动的反应很快
弹性供应
当任一供应的弹性大于一时,表明需求或供应的数量对价格变动反应良好
弹性
一种经济学概念,用于衡量一个变量对另一个变量变化的响应
非弹性需求
当需求弹性小于一时,表明消费者支付的价格上涨1%导致购买变化不到1%(反之亦然);这表明消费者对价格变动的反应不足
非弹性供应
当供应弹性小于一时,表示支付给公司的价格上涨1%将导致公司的产量增长不到1%;这表明公司对价格上涨的反应不足(如果价格下跌则反之亦然)
价格弹性
导致需求或供应数量相应百分比变化的价格变动百分比之间的关系
需求的价格弹性
商品或服务需求 数量的百分比变化除以价格变动百分比
供应的价格弹性
供应 数量的百分比变化除以价格变动百分比
单一弹性
当计算出的弹性等于 1 时,表示商品或服务价格的变化会导致需求或供应数量成比例的变化