26.5: 不断膨胀的宇宙
- Page ID
- 202875
学习目标
在本节结束时,您将能够:
- 描述一下随着宇宙的演变,星系之间的距离越来越远的发现
- 解释如何使用哈勃定律来确定与偏远星系的距离
- 描述不断膨胀的宇宙本质的模型
- 解释哈勃常数的变化
现在,我们来看看天文学有史以来最重要的发现之一——宇宙正在膨胀的事实。 在我们描述这一发现是如何做出之前,我们应该指出,星系研究的第一步是在光谱学技术也取得长足进步的时候采取的。 使用大型望远镜的天文学家可以在照相板上记录微弱的恒星或星系的光谱,引导他们的望远镜长时间指向同一个天体并收集更多的光。 由此产生的星系光谱包含有关银河系组成和这些伟大恒星系统速度的大量信息。
Slipher 的开创性观察
奇怪的是,宇宙扩张的发现始于寻找火星和其他太阳系。 1894年,备受争议(且富有)的天文学家珀西瓦尔·洛厄尔在亚利桑那州的弗拉格斯塔夫建立了一个天文台,以研究行星和寻找宇宙中的生命。 洛厄尔认为螺旋星云可能是正在形成的太阳系。 因此,他请天文台的一位年轻天文学家维斯托·斯利弗(Vesto M. Slipher\(\PageIndex{1}\))(图)拍摄一些螺旋星云的光谱,看看它们的光谱线是否会像新形成的行星所预期的那样显示出化学成分。

洛厄尔天文台的主要仪器是一台 24 英寸的折射望远镜,它根本不适合观测微弱的螺旋星云。 利用当时可用的技术,照相板必须曝光20到40个小时才能产生良好的光谱(线条的位置可以揭示星系的运动)。 这通常意味着要在几个晚上继续曝光同一张照片。 从1912年开始,Slipher在大约20年的时间里做出了英勇的努力,成功拍摄了40多个螺旋星云(原来都是星系)的光谱。
令他惊讶的是,大多数星系的光谱线显示出惊人的红移。 “红移” 是指光谱中的线向更长的波长(朝向可见光谱的红色端)移动。 回想一下关于辐射和光谱的章节,当波浪的源头从我们身边移开时,就会看到红移。 斯利弗的观察表明,大多数螺旋都在以极快的速度奔跑;他测得的最高速度为每秒 1800 千米。
事实证明,只有少数螺旋正在接近我们,例如仙女座星系和三角星系以及M81,所有这些螺旋现在都已知是我们的近邻。 所有其他星系都在离开。 Slipher 于 1914 年首次宣布了这一发现,早在哈勃证明这些天体是其他星系之前的几年,也没人知道它们有多远。 当时没有人完全知道这个发现该怎么做。
哈勃定律
Slipher 作品的深远影响直到 20 世纪 20 年代才显现出来。 乔治·勒迈特是一位比利时牧师和训练有素的天文学家。 1927 年,他在一本不起眼的比利时期刊上用法语发表了一篇论文,他在论文中暗示我们生活在一个不断膨胀的宇宙中。 该论文的标题(翻译成英文)是 “一个质量恒定、半径不断增长的同质宇宙,它解释了银河系外星云的径向速度。” 勒迈特发现爱因斯坦的相对论方程与不断膨胀的宇宙是一致的(1922年俄罗斯科学家亚历山大·弗里德曼独立也是如此)。 然后,勒迈特继续使用Slipher的数据来支持宇宙实际上在膨胀的假设并估计膨胀速度。 最初,科学家们很少关注这篇论文,这可能是因为比利时期刊尚未广泛发行。
同时,哈勃正在使用位于山上的2.5米望远镜对星系进行观测。 威尔逊,当时是世界上最大的公司。 哈勃与一位杰出人物米尔顿·胡马森合作进行了关键观测,米尔顿·胡马森八年级辍学,他的天文生涯始于驾驶一辆骡子列车沿着威尔逊山的小径前往天文台(图\(\PageIndex{2}\))。 在早期,补给品必须以这种方式运送;甚至天文学家也要徒步到山顶轮到望远镜看望远镜。 胡马森开始对天文学家的工作产生兴趣,在与天文台电工的女儿结婚后,在那里找到了一份看门人的工作。 过了一会儿,他成为了一名夜间助理,帮助天文学家运行望远镜并记录数据。 最终,他留下了如此深刻的印记,以至于他成为了天文台的正式天文学家。

到20世纪20年代末,Humason与哈勃合作,使用2.5米望远镜拍摄了微弱星系的光谱。 (那时,毫无疑问,螺旋星云实际上是星系。) 哈勃已经找到了提高螺旋星系距离估计精度的方法,而且他能够测量比斯利弗用小得多的望远镜所能观测到的更微弱、更远的星系。 当哈勃在测量衰退速度(星系离开的速度)旁边设定自己的距离估计值时,他发现了一些令人惊叹的东西:星系的距离和速度之间存在关系。 银河系越远,它从我们身边消退的速度就越快。
1931年,哈勃和胡马森共同发表了开创性的论文,他们在论文中比较了偏远星系以高达每秒20,000公里的速度离开我们的距离和速度,并得以证明星系的衰退速度与它们与我们的距离成正比(图\(\PageIndex{3}\)),正如勒迈特所建议的那样。
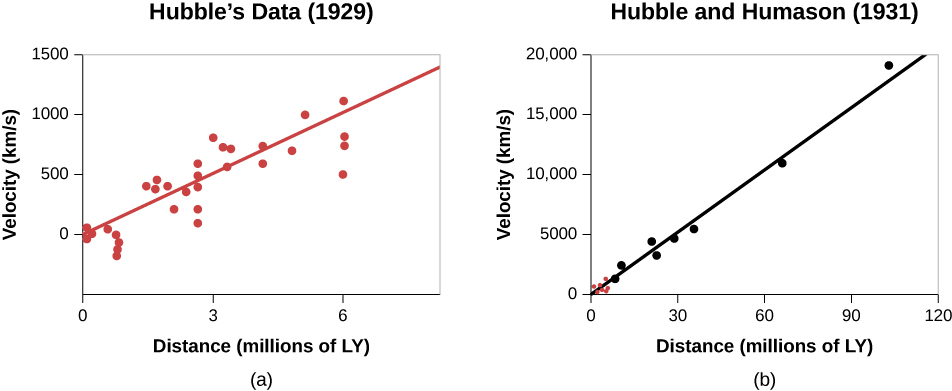
我们现在知道,除了几个最近的星系之外,这种关系适用于每个星系。 事实证明,几乎所有接近我们的星系都是银河系自己的星系群的一部分,这些星系有自己的单独运动,就像成群飞行的鸟类可能会以略有不同的方向飞行,尽管整群在太空中飞行一起。
用公式写成,速度和距离之间的关系是
\[v=H \times d \nonumber\]
哪里\(v\)是衰退速度,\(d\)是距离,\(H\)是一个叫做哈勃常数的数字。 这个方程现在被称为哈勃定律。
比例常数
诸如哈勃定律之类的数学关系在生活中很常见。 举一个简单的例子,假设你的学院或大学雇用你打电话给富有的校友并要求捐款。 每次通话可获得2.50美元的报酬;在学习天文学和其他课程之间可以拨打的电话越多,带回家的钱就越多。 我们可以设置一个公式来连接\(p\)您的工资和\(n\)通话次数
\[p=A \times n \nonumber\]
校友常数在\(A\)哪里,值为2.50美元。 如果你拨打20个电话,你将获得2.50美元乘以20或50美元。
假设你的老板忘记告诉你每次通话你将获得多少报酬。 你可以通过跟踪你打了多少电话并记下你每周的总工资来计算控制你薪水的校友常数。 如果您在第一周拨打100个电话并获得250美元的报酬,则可以推断出常数为2.50美元(以每次通话的美元为单位)。 当然,哈勃没有 “boss” 可以告诉他他的常数是多少 —— 他必须根据距离和速度的测量值来计算常数的值。
天文学家以单位表示哈勃常数的值,这些单位与他们如何测量星系的速度和速度有关。 在本书中,我们将使用每百万光年的千米每秒作为该单位。 多年来,对哈勃常数值的估计值一直在每百万光年每秒 15 到 30 千米之间。最近的研究似乎趋于接近每百万光年 22 千米/秒 If\(H\) 是每百万光年 22 千米/秒-年,一个星系每距离一百万光年就以每秒 22 千米的速度离开我们。 举个例子,一亿光年以外的星系正在以每秒 2200 千米的速度离开我们。
哈勃定律告诉我们一些关于宇宙的基本知识。 由于除了最近的星系以外的所有星系似乎都在远离我们的运动中,而最远的星系移动速度最快,因此我们必须生活在一个不断扩大的宇宙中。 我们将在不久以及本文的最后章节中探讨这个想法的含义。 现在,我们只想说哈勃的观察是我们所有关于宇宙起源和演变的理论的基础。
哈勃定律和距离
哈勃定律所表达的规律性有一个内在的好处:它为我们提供了一种确定与偏远星系距离的新方法。 首先,我们必须通过测量许多星系在多个方向上的距离和速度来可靠地建立哈勃常数,以确保哈勃定律确实是星系的普遍属性。 但是,一旦我们计算了这个常数的值并确信它适用于任何地方,就会有更多的宇宙空间可供确定距离。 基本上,如果我们能获得星系的光谱,我们就能立即分辨出它有多远。
程序是这样的。 我们使用光谱来测量星系远离我们的速度。 如果我们将这个速度和哈勃常数放入哈勃定律方程中,我们就可以求解距离。
示例\(\PageIndex{1}\):哈勃定律
哈勃定律 (\(v = H \times d\)) 允许我们计算到任何星系的距离。 以下是我们在实践中的使用方式。
我们测得的哈勃常数为每百万光年22 km/s。 这意味着,如果一个星系距离100万光年,它的移动速度将快22 km/s。 那么,如果我们发现一个以18,000 km/s的速度移动的星系,那么哈勃定律告诉我们与银河系的距离是什么?
解决方案
\[d = \frac{v}{H} = \frac{18,000 \text{ km/s}}{ \frac{22 \text{ km/s}}{1 \text{ million light-years}}} = \frac{18,000}{22} \times \frac{1 \text{ million light-years}{1} = 818 \text{ million light-years} \nonumber\]
注意我们是如何处理这里的单位的:分子和分母中的 km/s 抵消,在得到 8.18 亿光年的距离之前,必须正确除以常数分母中的百万光年系数。
练习\(\PageIndex{1}\)
使用22 km/s/百万光年作为哈勃常数,如果我们观测到一个5亿光年的星系,我们预计会发现多少衰退速度?
- 回答
-
\[v=d \times H = 500 \text{ million light-years} \times \frac{22 \text{ km/s}}{1 \text{ million light-years}} = 11,000 \text{ km/s} \nonumber\]
哈勃常数的变化
使用红移可能是确定距离的一种非常重要的技术,因为正如我们所看到的,我们确定星系距离的大多数方法都仅限于大约几亿光年(而且在这些距离上它们存在很大的不确定性)。 使用哈勃定律作为距离指示器只需要星系的光谱和对多普勒偏移的测量,而使用大型望远镜和现代光谱仪,可以对极其微弱的星系进行光谱。
但是,与科学界经常发生的情况一样,事情并不是那么简单。 当且仅当哈勃常数在宇宙的整个生命周期中一直保持不变时,这种技术才有效。 当我们在数十亿光年之外观察星系时,我们看到的是数十亿年前的星系。 如果哈勃的 “常数” 在数十亿年前有所不同怎么办? 在1998年之前,天文学家认为,尽管宇宙正在扩张,但扩张应该减慢或减速,因为宇宙中所有物质的总体引力将产生主导的、可测量的效应。 如果扩张正在减速,那么哈勃常数应该会随着时间的推移而降低。
Ia 型超新星是标准灯泡的发现为天文学家提供了观测极远星系和测量数十亿年前的膨胀速度所需的工具。 结果完全出乎意料。 事实证明,随着时间的推移,宇宙的扩张正在加速! 这个结果之所以如此令人震惊,是因为现有的物理理论无法解释这一观察。 虽然宇宙减速很容易用重力来解释,但天文学家所知道的宇宙中没有任何力量或特性可以解释加速的原因。 在《宇宙大爆炸》一章中,我们将更详细地研究导致这个完全出乎意料的结果的观测结果,并探讨它对宇宙终极命运的影响。
无论如何,如果当我们观察大跨度的空间和时间时,哈勃常数并不是一个真正的常数,那么使用哈勃常数计算星系距离就不准确了。 正如我们将在《大爆炸》一章中看到的那样,精确计算距离需要一个哈勃常数随时间变化的模型。 星系离得越远(而且我们看到的时间越长),将哈勃常数变化的影响包括在内就越重要。 但是,对于几十亿光年以内的星系,哈勃常数确实恒定的假设可以很好地估计距离。
膨胀宇宙的模型
起初,想想哈勃定律,成为哥白尼和哈洛·沙普利作品的粉丝,你可能会感到震惊。 所有的星系真的都在远离我们吗? 毕竟,我们在宇宙中的位置有什么特别之处吗? 不用担心;星系正在从我们身边消失,而且距离更远的星系的移动速度比附近的星系更快,这一事实仅表明宇宙正在均匀扩张。
均匀膨胀的宇宙是指在任何地方都以同样的速度扩张的宇宙。 在这样的宇宙中,我们和所有其他观察者,无论他们身在何处,都必须观察同等偏远星系的速度和距离之间的比例。 (在这里,我们忽略了这样一个事实,即哈勃常数并不是一直恒定的,但是如果在宇宙演变中的任何给定时间,哈勃常数在任何地方都有相同的值,那么这个论点仍然有效。)
要了解原因,首先想象一下用可拉伸的橡胶制成的尺子,每厘米处标出通常的线条。 现在假设有人用强壮的手臂抓住尺子的两端,然后慢慢地伸展它,比如说,它的长度在 1 分钟内翻了一番(图\(\PageIndex{4}\))。 假设一只聪明的蚂蚁坐在 2 厘米处的标记上,这个点既不在标尺的两端,也不在标尺的中间。 他测量坐在 4、7 和 12 厘米标记处的其他蚂蚁在尺子伸展时离开他的速度。

原本距离蚂蚁 2 厘米的距离 4 厘米的蚂蚁在 1 分钟内将其距离增加了一倍;因此,它以每分钟 2 厘米的速度移开。 原本距离蚂蚁 5 厘米的距离 7 厘米处的蚂蚁现在距离 10 厘米;因此,它必须以每分钟 5 厘米的速度移动。 始于 12 厘米大关的那个,距离正在计数的蚂蚁有 10 厘米的距离,现在已经有 20 厘米的距离了,这意味着它一定是以每分钟 10 厘米的速度跑开的。 不同距离的蚂蚁以不同的速度移开,它们的速度与它们的距离成正比(就像哈勃定律对星系所指出的那样)。 但是,请注意,在我们的例子中,统治者所做的只是均匀伸展。 另外,请注意,实际上没有一只蚂蚁是自行移动的,正是尺子的伸展使它们分开。
现在让我们重复分析,但要把聪明的蚂蚁放在另一个标记上,比如说,在 7 或 12 厘米处。 我们发现,只要标尺均匀伸展,这只蚂蚁还会发现其他所有蚂蚁都以与其距离成正比的速度移开。 换句话说,哈勃定律所表达的那种关系可以用蚂蚁 “世界” 的统一延伸来解释。 当标尺伸展时,我们简单图表中的所有蚂蚁都会看到其他蚂蚁从它们身边移开。
举个三维类比,让我们来看看 Figure 中的葡萄干面包\(\PageIndex{5}\)。 厨师不小心在面团里放了太多的酵母,当她把面包放出来时,它的大小在接下来的一个小时内会翻一番,导致所有的葡萄干相距更远。 在图中,我们再次选择一个具有代表性的葡萄干(不在面包的边缘或中心),并在图中(面包膨胀之前和之后)显示它与其他几个葡萄干的距离。
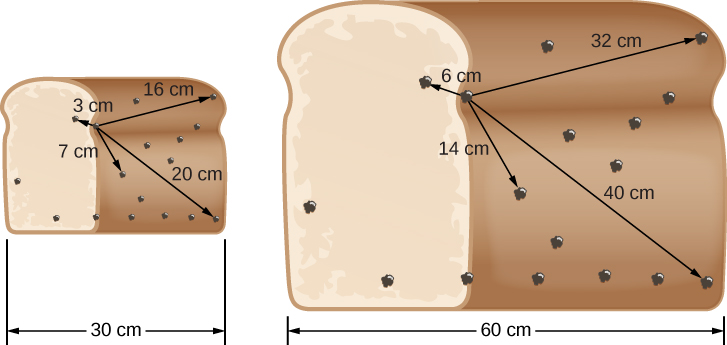
测量距离的增加,然后自己计算葡萄干面包的速度,就像我们为尺子做的那样。 你会看到,由于一小时内每个距离都会翻倍,因此每个葡萄干都会以与其距离成比例的速度离开我们选择的葡萄干。 不管你从哪个葡萄干开始,都是一样的。
我们的两个类比对于澄清我们的想法很有用,但你不能从字面上理解它们。 在尺子和葡萄干面包上,都有点在末端或边缘。 你可以用它们来精确定位尺子和面包的中间。 虽然我们的宇宙模型与统治者和面包的属性有些相似,但宇宙没有边界,没有边缘,也没有中心(我们将在后面的章节中讨论所有这些令人难以置信的想法)。
关于蚂蚁和葡萄干,值得注意的是,它们本身并没有 “引起” 它们的运动。 好像葡萄干没有决定彼此远离一段旅程然后跳上悬浮滑板逃脱。 不,在我们的两个类比中,正是媒介(尺子或面包)的拉伸使蚂蚁或葡萄干相距更远。 同样,我们将在《宇宙大爆炸》一章中看到,星系没有火箭发动机推动它们相互分离。 相反,他们是空间扩张的被动参与者。 随着空间的延伸,星系之间的距离越来越远,就像蚂蚁和葡萄干一样。 (如果这种太空 “拉伸” 的概念让你感到惊讶或困扰,那么现在是回顾《黑洞》和《曲线时空》中有关时空信息的好时机。 随着我们的讨论从星系扩展到整个宇宙,我们将进一步讨论这些想法。)
顺便说一句,宇宙的扩张并不意味着单个星系和星系团本身正在扩张。 用我们的比喻来说,葡萄干和蚂蚁的大小都不会随着面包的膨胀而变大。 同样,重力将星系和星系团凝聚在一起,随着宇宙的扩大,它们彼此之间的距离会越来越远,自身的大小不会改变。
摘要
宇宙正在膨胀。 观察表明,遥远星系的光谱线是红移的,它们的衰退速度与它们与我们的距离成正比,这种关系被称为哈勃定律。 衰退率被称为哈勃常数,约为每百万光年每秒22千米。 我们不是这次扩张的中心:任何其他星系中的观察者都会看到与我们相同的扩张模式。 最好将哈勃定律所描述的扩张理解为空间的延伸。
词汇表
- 哈勃常数
- 在将远程星系的速度与其距离联系起来的定律中,这是一个成比例的常数
- 哈勃定律
- 一条规则,即偏远星系的径向速度与它们与我们的距离成正比
- 红移
- 当光谱中的线向更长的波长(朝向可见光谱的红色端)移动时


