17.1: 星星的亮度

Last updated
Save as PDF

Page ID: 202639

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释亮度和表观亮度之间的区别
了解天文学家如何用量级指定亮度

亮度

也许恒星最重要的特征是它的亮度，即它每秒发射的所有波长下的总能量。早些时候，我们看到太阳每秒钟消耗大量的能量。（还有比太阳更亮的恒星。）为了便于在恒星之间进行比较，天文学家用太阳的亮度来表达其他恒星的亮度。例如，天狼星的亮度大约是太阳的25倍。我们使用符号 L _Sun 来表示太阳的亮度；因此，Sirius 的亮度可以写成 25 L S _un。在后面的章节中，我们将看到，如果我们能够测量一颗恒星发出的能量并知道它的质量，那么我们就可以计算出它在耗尽核能并开始死亡之前能持续发光多长时间。

表观亮度

天文学家谨慎区分恒星的亮度（总能量输出）和碰巧到达我们眼睛或地球上望远镜的能量。恒星在产生辐射的方式上是民主的；它们在太空的各个方向发射相同数量的能量。因此，恒星释放的能量中只有一小部分实际到达地球上的观察者手中。我们将地球上每秒到达给定区域（比如一平方米）的恒星能量称为表观亮度。如果你看夜空，你会看到星空中有各种各样的明显亮度。事实上，大多数恒星都很暗，你需要一台望远镜来探测它们。

如果所有恒星的亮度都一样——如果它们像标准灯泡一样具有相同的光输出——我们可以利用它们表观亮度的差异来告诉我们一些我们非常想知道的事情：它们有多远。想象一下，你在一个黑暗的大音乐厅或宴会厅里，除了在墙壁周围的灯具中放了几十个 25 瓦的灯泡。由于它们都是25瓦的灯泡，因此它们的亮度（能量输出）是相同的。但是从你站在一个角落的位置来看，它们的表面亮度并不相同。那些靠近你的人看起来更亮（更多的光线到达你的眼睛），而那些在你身边的人看起来更暗一些（它们的光线在到达你之前已经散开得更多）。通过这种方式，你可以分辨出哪些灯泡离你最近。同样，如果所有的恒星都具有相同的亮度，我们可以立即推断出最亮的恒星就在附近，而最暗的恒星则在很远的地方。

为了更准确地确定这个想法，回想一下《辐射与光谱》一章，我们确切地知道光是如何随着距离的增加而消失的。我们获得的能量与距离的平方成反比。例如，如果我们有两颗亮度相同的恒星，其中一颗的距离是另一颗的两倍，那么它看起来会比近的恒星暗四倍。如果它远三倍，它看起来会暗九倍（三平方），依此类推。

唉，星星的亮度并不相同。（实际上，我们对此感到非常高兴，因为拥有许多不同类型的恒星会使宇宙变得更加有趣。）但这意味着，如果一颗恒星在天空中看起来很暗，我们就无法分辨它看起来很暗是因为它的亮度较低但相对较近，还是因为它的亮度很高但距离很远。为了测量恒星的亮度，我们必须首先补偿距离对光线的暗淡影响，要做到这一点，我们必须知道它们有多远。距离是所有天文测量中最困难的测量之一。在我们了解了更多关于恒星的知识之后，我们将回到如何确定恒星的过程。现在，我们将描述天文学家如何确定恒星的表观亮度。

幅度等级

测量恒星表观亮度的过程称为光度测量（来自希腊照片的意思是 “光”，—metry 的意思是 “测量”）。当我们看到《观测天空：天文学的诞生》时，天文光度测量始于希帕丘斯。大约在公元前150年，他在地中海的罗得岛上建立了一个天文台。他在那里准备了将近1000颗恒星的目录，其中不仅包括它们的位置，还包括对它们表面亮度的估计。

Hipparchus 没有望远镜或任何可以精确测量视觉亮度的仪器，所以他只是用眼睛做了估计。他将恒星分为六个亮度类别，他称之为量级。他将目录中最亮的恒星称为一级恒星，而那些如此微弱以至于几乎看不见的恒星是六级恒星。在十九世纪，天文学家试图通过准确确定六级恒星的表观亮度与一级恒星的表观亮度有多大不同来使比例更加精确。测量结果表明，我们从一级恒星获得的光是来自六级恒星的100倍左右。根据这一测量结果，天文学家随后定义了一个精确的幅度系统，其中五个量级的差异恰好对应于 100:1 的亮度比。此外，恒星的大小是十进制的；例如，一颗恒星不只是 “二级恒星”，它的星级为2.0（或2.1、2.3等）。那么，当乘以五次时，这个系数是多少？在你的计算器上玩游戏，看看你能不能拿到它。答案约为 2.5，这是 100 的第五个根。这意味着一颗1.0级的恒星和一颗2.0级的恒星的亮度相差约为2.5倍。同样，我们从2.0级恒星获得的光大约是来自3.0级恒星的2.5倍。那么 1.0 级的恒星和 3.0 级的恒星有什么区别呢？由于每个 “步长” 的差异为2.5倍，因此亮度的总差异为2.5×2.5 = 6.25倍。

以下是一些经验法则，可能会对刚接触该系统的人有所帮助。如果两颗恒星相差0.75个星级，则它们的亮度相差约为2倍。如果它们相距 2.5 个量级，则它们的亮度相差为 10 倍，而 4 级差异对应于 40 倍的亮度差。此时你可能会对自己说：“为什么天文学家继续使用 2000 多年前的这个复杂系统？” 这是一个很好的问题，正如我们将要讨论的那样，今天的天文学家可以使用其他方式来表达恒星的亮度。但是由于这个系统仍在许多书籍、星图和计算机应用程序中使用，我们觉得我们必须向学生介绍它（尽管我们很想把它排除在外）。

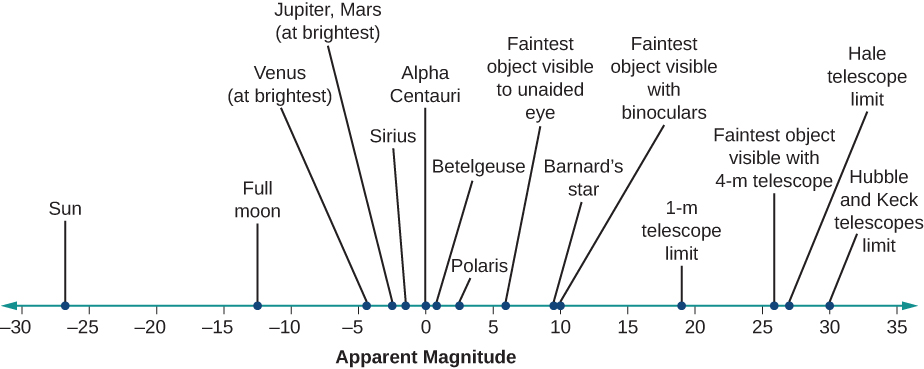
最亮的恒星，即传统上被称为一级恒星的恒星，实际上（如果精确测量）的亮度并不相同。例如，天空中最亮的恒星小天狼星向我们发出的光大约是普通一级恒星的10倍。在现代震级尺度上，视觉震级最亮的恒星小天狼星被分配了−1.5的星级。天空中的其他物体可能看起来更亮。金星最亮的幅度为−4.4，而太阳的震级为−26.8。该图\(\PageIndex{1}\)显示了观测到的从最亮到最微弱的幅度范围，以及几个已知物体的实际幅度。在使用幅度时要记住的重要事实是，系统会向后移动：幅度越大，所观察的物体就越微弱。

alt — 图\(\PageIndex{1}\)：已知物体的表观幅度。还显示了肉眼、双筒望远镜和大型望远镜可以探测到的最微弱的震级。

示例\(\PageIndex{1}\)：幅度方程

即使是科学家也无法计算出脑海中的第五个根，因此天文学家将上述讨论总结为一个方程式，以帮助计算不同大小的恒星的亮度差异。如果 m 1 和 m 2 是两颗恒星的大小，那么我们可以\(\left( \frac{b_2}{b_1} \right)\)使用以下方程计算它们的亮度之比：

\[m_1−m_2=2.5 \log \left( \frac{b_2}{b_1} \right) \text{ or } \frac{b_2}{b_1}=2.5^{m_1−m_2} \nonumber\]

这是写这个方程的另一种方法：

\[\frac{b_2}{b_1}= \left( 100^{0.2} \right)^{m_1−m_2} \nonumber\]

让我们举一个真实的例子，只是为了展示它是如何工作的。想象一下，一位天文学家发现了一颗昏暗的恒星（8.5 级）的特别之处，她想告诉学生这颗恒星比小天狼星暗多少。方程中的星星1将是我们的暗星，而星星2将是小天狼星。

解决方案

请记住，小天狼星的大小为 −1.5。在这种情况下：

\[\begin{aligned} \frac{b_2}{b_1} & = \left( 100^{0.2} \right)^{8.5−(−1.5)} =\left( 100^{0.2} \right)^{10} \\ ~ & =(100)^2=100×100=10,000 \end{aligned} \nonumber\]

练习\(\PageIndex{1}\)

人们普遍误解北极星（星级 2.0）是天空中最亮的恒星，但是，正如我们所见，这种区别实际上属于天狼星（星级 −1.5）。天狼星的表观亮度与北极星的表观亮度相比如何？

回答

\[ \frac{b_{\text{Sirius}}}{b_{\text{Polaris}}} = \left( 100^{0.2} \right)^{2.0−(−1.5)} = \left( 100^{0.2} \right)^{3.5} =100^{0.7}=25 \nonumber\]

（提示：如果你只有一个基本的计算器，你可能想知道如何用 100 到 0.7 次方。但这是你可以要求谷歌做的事情。谷歌现在接受数学问题并会回答。所以自己尝试一下。问问谷歌，“100 到 0.7 次的力量是多少？”）

我们的计算表明，天狼星的视在亮度是北极星视在亮度的25倍。

其他亮度单位

尽管震级尺度仍用于视觉天文学，但在该领域的新分支中根本没有使用它。例如，在射电天文学中，没有定义与幅度系统的等效物。相反，射电天文学家测量射电望远镜每平方米每秒收集的能量，并用每平方米瓦特等单位表示每个光源的亮度。

同样，红外、X射线和伽玛射线天文学领域的大多数研究人员使用每秒面积的能量而不是量级来表示测量结果。尽管如此，所有领域的天文学家都谨慎区分光源的亮度（即使这种亮度全部在 X 射线中）和碰巧到达地球上的能量。毕竟，亮度是一个非常重要的特征，它可以告诉我们有关物体的很多信息，而到达地球的能量则是宇宙地理学的意外。

为了便于比较恒星，在本文中，我们尽可能避免使用量级，而是用太阳的亮度来表示其他恒星的亮度。例如，天狼星的亮度是太阳的25倍。我们用这个符号\(L_{Sun}\)来表示太阳的亮度；因此，小天狼星的亮度可以写成 25\(L_{Sun}\)。

摘要

恒星每秒发射的总能量称为其亮度。从地球的角度来看，恒星的亮度是它的表观亮度。恒星的表观亮度既取决于它的亮度，也取决于它与地球的距离。因此，确定视在亮度和测量与恒星的距离可以提供足够的信息来计算其亮度。恒星的表观亮度通常用量级来表示，这是一个基于人类视觉如何解释相对光强的旧系统。

词汇表

表观亮度: 衡量地球从恒星或其他物体接收的光量，即物体在天空中的亮度与其亮度形成鲜明对比

发光: 恒星或其他物体向空间发射电磁能量的速率；物体的总功率输出

幅度: 测量我们从恒星或其他发光物体接收的光量的较旧系统；幅度越大，我们从物体接收的辐射就越少