Skip to main content
Global

11.4: الكواركات

  1. Last updated
  2. Save as PDF
  • Page ID
    196460

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • قارن وقارن بين الكواركات الستة المعروفة
    • استخدم تركيبة الكوارك للهيدرونات لتحديد الشحنة الكلية لهذه الجسيمات
    • شرح الدليل الأساسي لوجود الكواركات

    في الستينيات، بدأ علماء فيزياء الجسيمات يدركون أن الهادرونات ليست جزيئات أولية ولكنها مصنوعة من جزيئات تسمى الكواركات. (ابتكر الفيزيائي موراي جيل مان اسم «كوارك»، من عبارة في رواية جيمس جويس Finnegans Wake.) في البداية، كان يُعتقد أن هناك ثلاثة أنواع فقط من الكواركات، تسمى الأعلى (u) والأسفل (d) والغريبة (الغريبة). ومع ذلك، سرعان ما ارتفع هذا الرقم إلى ستة - ومن المثير للاهتمام أنه نفس عدد الليبتونات - ليشمل charmed (c) والأسفل (b) والعلوي (t).

    جميع الكواركات عبارة عن فرميونات\((s = 1/2)\) نصف دوارة ولها شحنة\(2/3 e)\) كسرية\((1/3\) أو لها رقم باريتون \(B = 1/3\). يحتوي كل كوارك على كوارك مضاد له نفس الكتلة ولكن بالشحنة المقابلة ورقم الباريون. يتم سرد أسماء وخصائص الكواركات الستة في الجدول.

    الجدول\(\PageIndex{1}\): باريتون كواركات
    كوارك الشحنة (وحدات من e) إسبانيا (إسبانيا) رقم باريون رقم الغرابة
    داون (د) - 1/3 1/2 1/3 0
    أعلى (يو) + 2/3 1/2 1/3 0
    غريب (س) - 1/3 1/2 1/3 - 1
    سحر (ج) + 2/3 1/2 1/3 0
    الجزء السفلي (ب) - 1/3 1/2 1/3 0
    أعلى (تي) + 2/3 1/2 1/3 0

    مجموعات كوارك

    كما ذكرنا سابقًا، ترتبط الكواركات معًا في مجموعات من اثنين أو ثلاثة لتشكيل الهادرونات. تتكون الباريونات من ثلاثة كواركات. وترد نماذج الباريونات، بما في ذلك محتوى الكوارك وخصائصه، في الجدول. ومن المثير للاهتمام أن الدلتا plus (\(\Delta^+\)) الباريون تتكون من نفس الكواركات الثلاثة التي يتكون منها البروتون، لكن الدوران الكلي للجسيم هو 3/2 بدلاً من 1/2. وبالمثل، فإن كتلة \(\Delta^+\) مع الدوران 3/2 تساوي 1.3 مرة كتلة البروتون، وباريون دلتا صفر (\(\Delta^0\)) ذو الدوران 3/2 يساوي 1.3 مرة كتلة النيوترون. من الواضح أن الطاقة المرتبطة بالدوران (أو الزخم الزاوي) للجسيم تساهم في طاقة كتلته. ومن المثير للاهتمام أيضًا أنه لا يُعتقد وجود باريونات في الكواركات العلوية، لأن الكواركات العلوية تتحلل بسرعة كبيرة بحيث لا يمكن ربطها بالكواركات الأخرى في إنتاجها.

    الجدول\(\PageIndex{2}\): باريتون كواركات
    اسم الرمز الكواركات الشحنة (وحدة إلكترونية) إسبانيا (إسبانيا) الكتلة \((GeV/c^2)\)
    بروتون ص يو يو دي 1 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 0.938
    نيوترون ن يو دي دي 0 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 0.940
    دلتا بلس بلس \(\Delta^{++}\) يو يو يو 2 3/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.232
    دلتا بلس \(\Delta^+\) يو يو دي 1 3/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.232
    دلتا زيرو \(\Delta^0\) يو دي دي 0 3/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.232
    دلتا ناقص \(\Delta^-\) د د د -1 3/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.232
    لامدا زيرو \(\Lambda^0\) يو دي إس 0 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.116
    سيغما إيجابية \(\Sigma^+\) يو يو إس 1 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.189
    سيغما محايدة \(\Sigma^0\) يو دي إس 0 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.192
    حادي عشر سلبي \(\Xi^-\) كما أفعل ذلك -1 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.321
    حادي عشر محايد \(\Xi_0\) كما هو الحال 0 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.315
    أوميغا ناقص \(\Omega^-\) كما هو الحال -1 3/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 1.672
    لامدا المسحورة \(\Lambda_{C+}\) يو دي سي 1 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 2.281
    قاع مسحور \(\Lambda_{b0}\) يو دي بي 0 1/2 \ (GEV/C^2)\)» النمط = «محاذاة النص: المركز؛» class="lt-phys-4557"> 5.612

    يتكون الميزون من كواركين - زوج من الكوارك والكوارك العتيق. يتم إعطاء عينات الميسونات، بما في ذلك محتوى الكوارك وخصائصه، في الجدول \(\PageIndex{3}\). ضع في اعتبارك تكوين البيون (\ (\ pi^+ = u\ الخط العلوي {d}\)). بناءً على محتواه من الكوارك، فإن شحنة الأسد هي

    \[\dfrac{2}{3}e + \dfrac{1}{3}e = e. \nonumber \]

    كلا الكواركات عبارة عن نصف دوران (\(s = \dfrac{1}{2}\))، وبالتالي فإن الدوران الناتج يكون إما 0 أو 1. دوران\((\pi^+)\) الميزون هو 0. نفس تركيبة الكوارك-أنتيكوارك تعطي الميزون rho (\(\rho\)) مع spin 1. تبلغ كتلة هذا الميزون حوالي 5.5 مرة من كتلة\(\pi^+\) الميزون.

    مثال\(\PageIndex{1}\): Quark Structure

    أظهر أن تركيبة الكوارك الواردة في الجدول\(\PageIndex{2}\) لـ\(\Xi^0\) تتوافق مع الشحنة والدوران والغرابة المعروفة لهذا الباريون.

    إستراتيجية

    \(\Xi^0\)يتكون من كواركين غريبين وكوارك علوي (s u s). يمكننا جمع خصائص الكواركات معًا للتنبؤ بالخصائص الناتجة\(\Xi^0\) للباريون.

    الحل

    شحنة الكوارك هي\(-e/3\) وشحنة الكوارك u هي 2 e /3. وبالتالي، لا توجد رسوم صافية على المجموعة (المجموعات)، بما يتفق مع التكلفة المعروفة لـ \(\Xi^0\). نظرًا لأن ثلاثة\(-1/2\) كواركات دونية يمكن أن تتحد لإنتاج جسيم يبلغ دورانه إما 1/2 أو 3/2، فإن تركيبة الكوارك تتوافق مع الدوران المعروف (\(s = 1/2\)) لـ\(\Xi^0\). أخيرًا، الغرابة الصافية لمجموعة (s u s) هي\ ((-1) + 0 + (-1) = -2\)، والتي تتوافق أيضًا مع التجربة.

    الأهمية

    يمكن تحديد شحنة\(\Xi^0\) الجسيم ودورانه وغرابته من خلال خصائص الكواركات المكونة له. يمكن إرجاع التنوع الكبير للباريونات والميزون إلى خصائص ستة كواركات فقط: أعلى وأسفل وشحنة وغريبة وأعلى وأسفل.

    التمارين الرياضية\(\PageIndex{1}\)

    ما هو رقم الباريون لبيون؟

    إجابة

    0

    الجدول\(\PageIndex{3}\): ميزون كواركات
    اسم الرمز الكواركات الشحنة (الإلكترونية) سبين الكتلة\((GeV/c^2)\)
    أسد إيجابي \(\pi^+\) \(u\overline{d}\) 1 0 \ ((GEV/C^2)\) ">0.140
    روح إيجابية \(\rho^+\) \(u\overline{d}\) 1 1 \ ((GEV/C^2)\) ">0.768
    بيون سالب \(\pi^-\) \(\overline{u}d\) -1 0 \ ((GEV/C^2)\) ">0.140
    خطأ سلبي \(\rho^-\) \(\overline{u}d\) -1 1 \ ((GEV/C^2)\) ">0.768
    أسد محايد \(\pi^0\) \(\overline{u}u\)أو \(\overline{d}d\) 0 0 \ ((GEV/C^2)\) ">0.135
    شاي محايد \(\eta^0\) \ (\ الخط العلوي {u} u،\، \ الخط العلوي {d} d\) أو\(\overline{s}s\) 0 0 \ ((GEV/C ^2)\) ">0.547
    سبب إيجابي \(K^+\) \(u\overline{s}\) 1 0 \ ((GEV/C^2)\) ">0.494
    كاون محايد \(K^0\) \(d\overline{s}\) 0 0 \ ((GEV/C^2)\) ">0.498
    كاون سالب \(K^-\) \(\overline{u}s\) -1 0 \ ((GEV/C^2)\) ">0.494
    جيه لكل بوصة مربعة \(J/\psi\) \(\overline{c}c\) 0 1 \ ((GEV/C^2)\) ">3.10
    شاي مسحور \(\eta_0\) \(c\overline{c}\) 0 0 \ ((GEV/C^2)\) ">2.98
    حرف D محايد \(D^0\) \(\overline{u}c\) 0 0 \ ((GEV/C^2)\) ">1.86
    حرف D محايد \(D^{*0}\) \(\overline{u}c\) 0 1 \ ((GEV/C^2)\) ">2.01
    معرف إيجابي \(D^+\) \(\overline{d}c\) 1 0 \ ((GEV/C^2)\) ">1.87
    محايد ب \(B^0\) \(\overline{d}b\) 0 0 \ ((GEV/C^2)\) ">5.26
    أبسيلون \(\Upsilon\) \(b\overline{b}\) 0 1 \ ((GEV/C^2)\) ">9.46

    اللون

    الكواركات هي فرميونات تخضع لمبدأ باولي للاستبعاد، لذلك قد يكون من المفاجئ معرفة أن الكواركات الثلاثة يمكن أن تتحد معًا داخل النواة. على سبيل المثال، كيف يمكن أن يوجد كوارك مزدوج في نفس المنطقة الصغيرة من الفضاء داخل البروتون؟ الحل هو ابتكار خاصية جديدة ثالثة لتمييزها. هذه الخاصية تسمى اللون، وتلعب نفس الدور في التفاعل النووي القوي مثل الشحنة في التفاعلات الكهرومغناطيسية. لهذا السبب، يُطلق على لون الكوارك أحيانًا اسم «الشحنة القوية».

    تأتي الكواركات بثلاثة ألوان: الأحمر والأخضر والأزرق. (هذه مجرد ملصقات - الكواركات ليست ملونة فعليًا.) \((u, \, d, \, c, \, s, \, b, \, t)\)يمكن أن يمتلك كل نوع من أنواع الكوارك أي ألوان أخرى. على سبيل المثال، توجد ثلاثة كواركات غريبة: كوارك أحمر غريب وكوارك غريب أخضر وكوارك أزرق غريب. مضادات الكواركات لها لون مضاد. يجب أن تكون الكواركات التي تتجمع معًا لتكوين الهادرونات ( الباريونات والميزون) محايدة اللون أو عديمة اللون أو «بيضاء». وبالتالي، يجب أن يحتوي الباريتون على كوارك أحمر وأزرق وأخضر. وبالمثل، يحتوي الميزون إما على زوج كوارك باللون الأحمر أو الأحمر أو الأزرق المضاد للأزرق أو الأخضر-المضاد للأخضر. وهكذا، يمكن العثور على الكواركات في نفس حالة الدوران في الهادرون، دون انتهاك مبدأ باولي للاستبعاد، لأن ألوانها مختلفة.

    حبس الكوارك

    أول دليل قوي على وجود الكواركات جاء من سلسلة من التجارب التي أجريت في مركز ستانفورد للمسرع الخطي (SLAC) وفي CERN حوالي عام 1970. تم تصميم هذه التجربة لاستكشاف بنية البروتون، مثلما درس رذرفورد البنية داخل الذرة من خلال تجاربه \(\alpha\) في تشتت الجسيمات. اصطدمت الإلكترونات بالبروتونات بطاقة تزيد عن 20 GeV. عند هذه الطاقة،\ (E \ تقريبًا pc\)، يكون طول موجة دي برولي للإلكترون هو

    \ [\ لامدا =\ dfrac {h} {p} =\ dfrac {hc} {E}\ تقريبًا 6\ مرات 10 ^ {-17} م.\ لا رقم\]

    الطول الموجي للإلكترون أصغر بكثير من قطر البروتون (حوالي\(10^{-15} m)\). وهكذا، مثل سيارة تسير عبر سلسلة جبال صخرية، يمكن استخدام الإلكترونات لاستكشاف بنية النواة.

    وجدت تجارب SLAC أن بعض الإلكترونات انحرفت بزوايا كبيرة جدًا، مما يشير إلى مراكز تشتت صغيرة داخل البروتون. كان توزيع التشتت متسقًا مع تشتت الإلكترونات من المواقع ذات الدوران 1/2، وهو دوران الكواركات. استخدمت التجارب في CERN النيوترينوات بدلاً من الإلكترونات. وجدت هذه التجربة أيضًا أدلة على مراكز التشتت الصغيرة. في كلتا التجربتين، أشارت النتائج إلى أن شحنات الجسيمات المتناثرة كانت إما\(+2/3e\) أو\(-1/3 e\) متوافقة مع نموذج الكوارك.

    ما هي الكواركات؟ إصدار السكر!

    شاهد هذا الفيديو لمعرفة المزيد عن الكواركات.

    تتكون البروتونات والنيوترونات من ثلاثة كواركات، أليس كذلك؟ خطأ! استكشف الجسيم الذي كان يجب أن يخبروك به عندما كنت طفلاً!

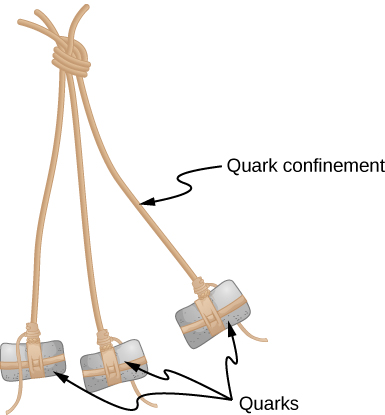
    كان نموذج الكوارك ناجحًا للغاية في تنظيم العالم المعقد للجسيمات دون الذرية. ولكن من المثير للاهتمام أنه لم تنتج أي تجربة كوارك معزول. تحتوي جميع الكواركات على شحنة كسرية وبالتالي يجب تمييزها بسهولة عن الجسيمات الأولية المعروفة، والتي تكون شحناتها كلها عددًا صحيحًا مضاعفًا لـ e. لماذا لا يتم ملاحظة الكواركات المعزولة؟ في النماذج الحالية لتفاعلات الجسيمات، يتم التعبير عن الإجابة من حيث حصر الكوارك. يشير حصر الكواركات إلى حصر الكواركات في مجموعات من اثنين أو ثلاثة في منطقة صغيرة من الفضاء. والكواركات حرة تمامًا في التحرك في هذا الفضاء وإرسال واستقبال الجلوونات (حاملات القوة القوية). ومع ذلك، إذا ابتعدت هذه الكواركات كثيرًا عن بعضها البعض، فإن القوة القوية تسحبها إلى الخلف. يُشبه هذا الإجراء بالبولا، وهو سلاح يستخدم للصيد (الشكل\(\PageIndex{1}\)). يتم ربط الأحجار بنقطة مركزية بواسطة خيط، لذلك لا يمكن لأي من الصخور أن تتحرك بعيدًا جدًا عن الصخور الأخرى. تتطابق البولا مع الباريون، وتتوافق الأحجار مع الكواركات، وتتوافق السلسلة مع الغلوونات التي تربط النظام معًا.

    يتم ربط ثلاث سلاسل معًا في أحد طرفيها. يتم ربط الوزن بالطرف الآخر من كل منهما. يُطلق على الأوتار اسم «حبس الكوارك». يتم تسمية الأوزان بالكواركات.
    الشكل\(\PageIndex{1}\): الباريون يشبه البولا، وهو سلاح يستخدم للصيد. تتطابق الصخور في هذه الصورة مع كواركات الباريون. والكواركات حرة في التحرك ولكن يجب أن تظل قريبة من الكواركات الأخرى.