10.7: الاندماج النووي
- Page ID
- 196729
في نهاية هذا القسم، ستكون قادرًا على:
- وصف عملية الاندماج النووي من حيث منتجها ومفاعلاتها
- احسب طاقات الجسيمات الناتجة عن تفاعل الاندماج
- شرح مفهوم الانشطار في سياق القنابل الاندماجية، وإنتاج الطاقة من الشمس، والتركيب النووي
تسمى عملية الجمع بين النوى الأخف لصنع نوى أثقل بالاندماج النووي. كما هو الحال مع تفاعلات الانشطار، تكون تفاعلات الاندماج طاردة للحرارة - فهي تطلق الطاقة. لنفترض أننا ندمج نوى الكربون والهيليوم لإنتاج الأكسجين:
\[\ce{_6^{12}C + _2^4He \rightarrow _8^{16}O + \gamma.} \nonumber \]
يمكن فهم تغيرات الطاقة في هذا التفاعل باستخدام رسم بياني لطاقة الربط لكل نواة. وبمقارنة طاقة الربط لكل نواة للأكسجين والكربون والهيليوم، تكون نواة الأكسجين أكثر ارتباطًا من نوى الكربون والهيليوم، مما يشير إلى أن التفاعل ينتج انخفاضًا في طاقة النظام. يتم إطلاق هذه الطاقة في شكل أشعة جاما. يُقال إن تفاعلات الاندماج تكون طاردة للحرارة عندما تكون كمية الطاقة المنبعثة (المعروفة باسم قيمة Q) في كل تفاعل أكبر من الصفر\((Q > 0)\).
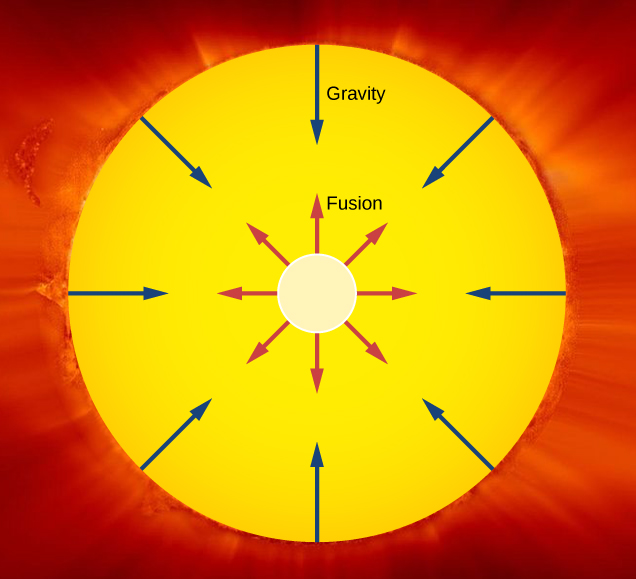
من الأمثلة المهمة للاندماج النووي في الطبيعة إنتاج الطاقة في الشمس. في عام 1938، اقترح هانز بيث أن تنتج الشمس الطاقة عندما تندمج نوى الهيدروجين (\(\ce{^1H}\)) في نوى الهيليوم المستقرة (\(\ce{^{4}He}\)) في قلب الشمس (الشكل\(\PageIndex{1}\)). يتم تلخيص هذه العملية، التي تسمى سلسلة البروتون-البروتون، من خلال ثلاثة تفاعلات:
\[ \begin{align} \ce{_1^1H + _1^1H} & \rightarrow \ce{_1^2H + _1^0e + \nu + Q,} \\[4pt] \ce{_1^1H + _1^2H} &\rightarrow \ce{_2^3He + \gamma + Q,} \\[4pt] \ce{_2^3He + _2^3He} &\rightarrow \ce{_2^4He + _1^1H + _1^1H + Q.} \end{align} \nonumber \]
وهكذا، تتشكل نواة هيليوم مستقرة من اندماج نوى ذرة الهيدروجين. يمكن تلخيص ردود الفعل الثلاثة هذه من خلال
\[\ce{4_1^1H \rightarrow _2^4He + 2_1^0e + 2\gamma + 2\nu + Q.} \nonumber \]
تبلغ قيمة Q الصافية حوالي 26 MeV. ينتج عن إطلاق هذه الطاقة ضغط غاز حراري خارجي يمنع الشمس من الانهيار الجاذبي. يجد علماء الفيزياء الفلكية أن اندماج الهيدروجين يوفر الطاقة التي تحتاجها النجوم للحفاظ على توازن الطاقة طوال معظم فترة حياة النجم.
تخليق نووي
يعتقد العلماء الآن أن العديد من العناصر الثقيلة الموجودة على الأرض وفي جميع أنحاء الكون تم تصنيعها في الأصل عن طريق الاندماج داخل النوى الساخنة للنجوم. تُعرف هذه العملية بالتخليق النووي. على سبيل المثال، في النجوم الأخف، يتحد الهيدروجين لتكوين الهيليوم من خلال سلسلة البروتون-البروتون. بمجرد استنفاد وقود الهيدروجين، يدخل النجم المرحلة التالية من حياته ويدمج الهيليوم. مثال على سلسلة التفاعل النووي التي يمكن أن تحدث هو:
\[\ce{_2^4He + _2^4He \rightarrow _4^8Be + \gamma,} \nonumber \]
\[\ce{_4^8Be + _2^4He \rightarrow _6^{12}C + \gamma,} \nonumber \]
\[\ce{_6^{12}C + _2^4He \rightarrow _8^{16}O + \gamma.} \nonumber \]
تصل نوى الكربون والأكسجين المنتجة في مثل هذه العمليات في النهاية إلى سطح النجم بالحمل الحراري. قرب نهاية عمره، يفقد النجم طبقاته الخارجية في الفضاء، مما يثري الوسط بين النجوم بنواة العناصر الثقيلة (الشكل\(\PageIndex{2}\)).
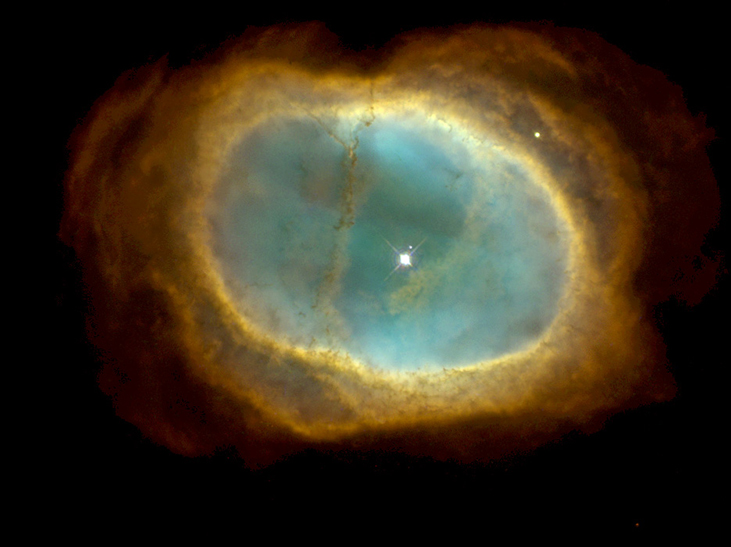
لا تصبح النجوم المشابهة في الكتلة للشمس ساخنة بدرجة كافية لدمج نوى ثقيلة (أو أثقل) من نوى الأكسجين. ومع ذلك، في النجوم الضخمة التي تصبح نواتها أكثر سخونة\((T > 6 \times 10^8 \, K)\)، يتم إنتاج نوى أكثر تعقيدًا. بعض ردود الفعل التمثيلية هي
\[\ce{_6^{12}C + _6^{12}C \rightarrow _{11}^{23}Na + _1^1H,} \nonumber \]
\[\ce{_6^{12}C + _6^{12}C \rightarrow _{12}^{24}Mg + \gamma,} \nonumber \]
\[\ce{_6^{12}C + _8^{16}O \rightarrow _{14}^{28}Si + \gamma.} \nonumber \]
يستمر التخليق النووي حتى يتكون اللب بشكل أساسي من معدن الحديد والنيكل. الآن، يمتلك الحديد خاصية مميزة تتمثل في أن أي تفاعل اندماج أو انشطار يشمل نواة الحديد هو ماص للحرارة، مما يعني أن الطاقة يتم امتصاصها بدلاً من إنتاجها. وبالتالي، لا يمكن توليد الطاقة النووية في نواة غنية بالحديد. نظرًا لعدم وجود ضغط خارجي من تفاعلات الاندماج، يبدأ النجم في الانقباض بسبب الجاذبية. تقوم هذه العملية بتسخين النواة إلى درجة حرارة بالترتيب\(5 \times 10^9K\). تتسبب موجات الصدمة المتسعة المتولدة داخل النجم بسبب الانهيار في انفجار النجم بسرعة. يمكن أن يزداد لمعان النجم مؤقتًا إلى ما يقرب من مجرة بأكملها. خلال هذا الحدث، يتفاعل تدفق النيوترونات النشطة مع الحديد والنواة الأخرى لإنتاج عناصر أثقل من الحديد. يتم إخراج هذه العناصر، إلى جانب جزء كبير من النجم، إلى الفضاء بسبب الانفجار. تلعب المستعرات الأعظمية وتشكيل السديم الكوكبية معًا دورًا رئيسيًا في تشتت العناصر الكيميائية في الفضاء.
في نهاية المطاف، يتم جمع الكثير من المواد التي فقدتها النجوم معًا من خلال قوة الجاذبية، وتتكثف لتصبح جيلًا جديدًا من النجوم والكواكب المصاحبة. تقدم الصور الحديثة من تلسكوب هابل الفضائي لمحة عن هذه العملية الرائعة التي تجري في كوكبة Serpens (الشكل\(\PageIndex{3}\)). يبدأ الجيل الجديد من النجوم عملية التخليق النووي من جديد، مع نسبة أعلى من العناصر الثقيلة. وبالتالي، فإن النجوم هي «مصانع» للعناصر الكيميائية، والعديد من الذرات في أجسامنا كانت ذات يوم جزءًا من النجوم.

يبلغ خرج الطاقة من الشمس تقريبًا\(3.8 \times 10^{26} J/s\). يتم إنتاج معظم هذه الطاقة في قلب الشمس من خلال سلسلة البروتون-البروتون. تنتقل هذه الطاقة إلى الخارج من خلال عمليات الحمل الحراري والإشعاع.
- ما عدد تفاعلات الاندماج هذه في الثانية التي يجب أن تحدث لتوفير الطاقة التي تشعها الشمس؟
- ما معدل انخفاض كتلة الشمس؟
- في حوالي خمسة مليارات سنة، سيتم استنفاد النواة المركزية للشمس من الهيدروجين. ما النسبة المئوية التي ستنخفض بها كتلة الشمس عن قيمتها الحالية عند استنفاد النواة من الهيدروجين؟
إستراتيجية
يتم إعطاء إجمالي إنتاج الطاقة في الثانية في بيان المشكلة. إذا عرفنا الطاقة المنبعثة في كل تفاعل اندماج، يمكننا تحديد معدل تفاعلات الاندماج. إذا كان فقدان الكتلة لكل تفاعل اندماج معروفًا، فإن معدل فقدان الكتلة معروف. ضرب هذا المعدل في خمسة مليارات سنة يعطي الكتلة الكلية التي فقدتها الشمس. يتم تقسيم هذه القيمة على الكتلة الأصلية للشمس لتحديد النسبة المئوية لكتلة الشمس المفقودة عند استنفاد وقود الهيدروجين.
الحل
- الانخفاض في الكتلة لتفاعل الاندماج هو الطاقة\[\begin{align*} \Delta m &= 4m (_1^1H) - m(_2^4He) - 2m(_1^0e) \\[4pt] &= 4(1.007825 \, u) - 4.002603 \, u = 2(0.000549 \, u) \\[4pt] &= 0.0276 \, u. \end{align*} \nonumber \] المنبعثة لكل تفاعل اندماج،\[Q = (0.0276 \, u)(931.49 \, MeV/u) = 25.7 \, MeV. \nonumber \] وبالتالي، للتزويد\(3.8 \times 10^{26} J/s = 2.38 \times 10^{39} MeV/s\)، يجب أن يكون هناك\[\frac{2.38 \times 10^{39} MeV/s}{25.7 \, MeV/reaction} = 9.26 \times 10^{37} \, reaction/s. \nonumber \]
- تنخفض كتلة الشمس بمقدار\(0.0276 \, u = 4.58 \times 10^{-29}kg\) كل تفاعل اندماج، وبالتالي فإن معدل انخفاض كتلتها هو\[(9.26 \times 10^{37} reaction/s)(4.58 \times 10^{-29} kg/reaction) = 4.24 \times 10^9 kg/s. \nonumber \]
- وبالتالي ستنخفض كتلة الشمس بمقدار الكتلة الحالية\[ \begin{align*} \Delta M &= (4.24 \times 10^9 kg/s)(1.6 \times 10^{17}s) \\[4pt] &= 6.8 \times 10^{26}kg.\end{align*} \nonumber \] للشمس تقريبًا\(2.0 \times 10^{30} kg\)، وبالتالي فإن النسبة المئوية للانخفاض في كتلتها عند استنفاد وقود الهيدروجين ستكون\(5 \times 10^9 \, y = 1.6 \times 10^{17}s\)\[\left(\frac{6.8 \times 10^{26}kg}{2.0 \times 10^{30}kg}\right) \times 100\% = 0.034\%. \nonumber \]
الدلالة
بعد خمسة مليارات سنة، أصبحت الشمس تقريبًا نفس الكتلة التي هي عليها الآن. لا يفعل حرق الهيدروجين سوى القليل لتغيير كتلة الشمس. يفترض هذا الحساب أن تغير تحلل البروتون والبروتون فقط هو المسؤول عن خرج الطاقة من الشمس.
من أين تأتي الطاقة من الشمس؟
- إجابة
-
تحويل الكتلة إلى طاقة
القنبلة الهيدروجينية
في عام 1942، اقترح روبرت أوبنهايمر أنه يمكن استخدام درجة الحرارة المرتفعة للغاية للقنبلة الذرية لتحفيز تفاعل الاندماج بين الديوتيريوم والتريتيوم، وبالتالي إنتاج قنبلة انصهار (أو هيدروجينية). يتم إعطاء التفاعل بين الديوتيريوم والتريتيوم، وكلاهما نظير للهيدروجين، بواسطة
\[\ce{_1^2H + _1^3H \rightarrow _2^4He + _0^1n} + 17.6 \, MeV. \nonumber \]
الديوتيريوم وفير نسبيًا في مياه المحيط، لكن التريتيوم نادر. ومع ذلك، يمكن توليد التريتيوم في مفاعل نووي من خلال تفاعل يشمل الليثيوم. تتسبب النيوترونات من المفاعل في التفاعل
\[\ce{_0^1n + _3^7Li \rightarrow _2^4He + _1^3H + _0^1n}, \nonumber \]
لإنتاج التريتيوم المطلوب. تم تفجير أول قنبلة هيدروجينية في عام 1952 في جزيرة إنيويتوك النائية في جزر مارشال. لم يتم استخدام قنبلة هيدروجينية في الحرب. تعد القنابل الهيدروجينية الحديثة أقوى بحوالي 1000 مرة من القنابل الانشطارية التي أسقطت على هيروشيما وناغازاكي في الحرب العالمية الثانية.
مفاعل فيوجن
يُعتقد أن سلسلة الاندماج الأكثر عملية للاستخدام في مفاعل الاندماج النووي هي العملية التالية المكونة من خطوتين:
\[\ce{_1^2H + _1^2H \rightarrow _1^3H + _1^1H}, \nonumber \]
\[\ce{_1^2H + _1^3H \rightarrow _2^4He + _0^1n}. \nonumber \]
تنتج هذه السلسلة، مثل سلسلة البروتون-البروتون، الطاقة دون أي منتج ثانوي مشع. ومع ذلك، هناك مشكلة صعبة للغاية يجب التغلب عليها قبل استخدام الاندماج لإنتاج كميات كبيرة من الطاقة:\((\approx 10^7 \, K)\) هناك حاجة إلى درجات حرارة عالية للغاية لدفع عملية الاندماج. ولمواجهة هذا التحدي، يجري تطوير مفاعلات الاندماج الاختباري لتحمل درجات حرارة تزيد 20 مرة عن درجة حرارة الشمس الأساسية. ومن الأمثلة على ذلك الجولات الأوروبية المشتركة (JET) الموضحة في الشكل\(\PageIndex{4}\). لا يزال هناك الكثير من العمل الذي يتعين القيام به في مجال تكنولوجيا مفاعل الاندماج، لكن العديد من العلماء يتوقعون أن طاقة الاندماج ستزود مدن العالم بالطاقة بحلول نهاية القرن العشرين.



