6.7: ثنائية الموجة والجسيمات
- Page ID
- 196582
في نهاية هذا القسم، ستكون قادرًا على:
- حدد الظواهر التي تتصرف فيها الموجات الكهرومغناطيسية مثل شعاع من الفوتونات وتتصرف الجسيمات مثل الموجات
- وصف المبادئ الفيزيائية وراء الفحص المجهري الإلكتروني
- تلخيص تطور الفكر العلمي الذي أدى إلى تطوير ميكانيكا الكم
تأتي طاقة الإشعاع المكتشفة بواسطة هوائي استقبال الإشارات الراديوية كطاقة للموجة الكهرومغناطيسية. تأتي نفس طاقة الإشعاع المكتشفة بواسطة التيار الضوئي في التأثير الكهروضوئي كطاقة لجسيمات الفوتون الفردية. لذلك، يطرح السؤال حول طبيعة الإشعاع الكهرومغناطيسي: هل الفوتون موجة أم أنه جسيم؟ قد يتم طرح أسئلة مماثلة حول أشكال الطاقة المعروفة الأخرى. على سبيل المثال، يتصرف الإلكترون الذي يشكل جزءًا من تيار كهربائي في الدائرة كجسيم يتحرك في انسجام مع إلكترونات أخرى داخل الموصل. يعمل الإلكترون نفسه كموجة عندما يمر عبر بنية بلورية صلبة ويشكل صورة حيود. هل الإلكترون موجة أم جسيم؟ يمكن توسيع نفس السؤال ليشمل جميع جزيئات المادة - الجسيمات الأولية، وكذلك الجزيئات المركبة - التي تسأل عن طبيعتها الفيزيائية الحقيقية. في حالة معرفتنا الحالية، لا تحتوي مثل هذه الأسئلة حول الطبيعة الحقيقية للأشياء على إجابات قاطعة. كل ما يمكننا قوله هو أن ثنائية الموجة والجسيمات موجودة في الطبيعة: في ظل بعض الظروف التجريبية، يبدو أن الجسيم يعمل كجسيم، وفي ظل ظروف تجريبية مختلفة، يبدو أن الجسيم يعمل كموجة. على العكس من ذلك، في بعض الظروف المادية، يعمل الإشعاع الكهرومغناطيسي كموجة، وفي ظل ظروف فيزيائية أخرى، يعمل الإشعاع كحزمة من الفوتونات.
هذا التفسير المزدوج ليس مفهومًا فيزيائيًا جديدًا أحدثته اكتشافات محددة في القرن العشرين. كانت موجودة بالفعل في نقاش بين إسحاق نيوتن وكريستيان هويغنز حول طبيعة الضوء، بدءًا من عام 1670. وفقًا لنيوتن، فإن شعاع الضوء عبارة عن مجموعة من جزيئات الضوء. وفقًا لـ Huygens، فإن الضوء عبارة عن موجة. فشلت الفرضية الجسيمية في عام 1803، عندما أعلن توماس يونغ عن تجربته للتداخل المزدوج مع الضوء (انظر الشكل\(\PageIndex{1}\))، والتي رسخت الضوء كموجة. في نظرية جيمس كليرك ماكسويل للكهرومغناطيسية (اكتملت بحلول عام 1873)، الضوء عبارة عن موجة كهرومغناطيسية. لا تزال رؤية ماكسويل الكلاسيكية للإشعاع كموجة كهرومغناطيسية صالحة اليوم؛ ومع ذلك، فهي غير قادرة على تفسير إشعاع الجسم الأسود والتأثير الكهروضوئي، حيث يعمل الضوء كشعاع من الفوتونات.
يوجد انقسام مماثل في تفسير الكهرباء. من ملاحظات بنجامين فرانكلين للكهرباء في عام 1751 حتى اكتشاف جي جي طومسون للإلكترون في عام 1897، كان يُنظر إلى التيار الكهربائي على أنه تدفق في وسط كهربائي مستمر. ضمن نظرية السائل الكهربائي هذه، تم تطوير النظرية الحالية للدوائر الكهربائية، وتم اكتشاف الكهرومغناطيسية والتحريض الكهرومغناطيسي. أظهرت تجربة طومسون أن وحدة الشحنة الكهربائية السالبة (الإلكترون) يمكن أن تنتقل في فراغ بدون أي وسيط لحمل الشحنة، كما هو الحال في الدوائر الكهربائية. أدى هذا الاكتشاف إلى تغيير الطريقة التي يتم بها فهم الكهرباء اليوم وأعطى الإلكترون حالة الجسيمات. في نظرية بوهر الكمومية المبكرة لذرة الهيدروجين، يعتبر كل من الإلكترون والبروتون جزيئات من المادة. وبالمثل، في تشتت كومبتون للأشعة السينية على الإلكترونات، يكون الإلكترون جسيمًا. من ناحية أخرى، في تجارب تشتت الإلكترون على الهياكل البلورية، يتصرف الإلكترون كموجة.
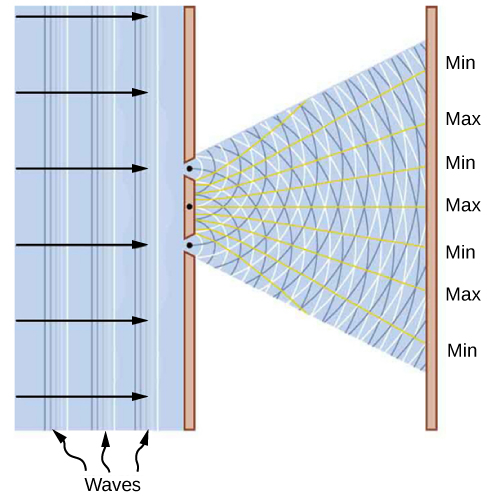
قد يثير أحد المتشككين سؤالًا مفاده أنه ربما لا يكون الإلكترون دائمًا أكثر من مجرد جسيم، وأن صور الحيود التي تم الحصول عليها في تجارب تشتت الإلكترون يمكن تفسيرها في بعض النماذج العيانية للبلورة والنموذج المجهري للإلكترونات القادمة إليها مثل مطر بينج بونج كرات. في الواقع، للتحقيق في هذا السؤال، لا نحتاج إلى نموذج معقد من البلورة ولكن فقط بضع شقوق بسيطة في شاشة غير شفافة بالنسبة للإلكترونات. بعبارة أخرى، لجمع أدلة مقنعة حول طبيعة الإلكترون، نحتاج إلى تكرار تجربة يونغ ذات الشق المزدوج مع الإلكترونات. إذا كان الإلكترون عبارة عن موجة، فيجب أن نلاحظ تكوين أنماط التداخل النموذجية للموجات، مثل تلك الموضحة في الشكل\(\PageIndex{1}\)، حتى عندما تمر الإلكترونات عبر الشقوق واحدة تلو الأخرى. ومع ذلك، إذا لم يكن الإلكترون موجة بل جسيمًا، فلن تتشكل أطراف التداخل.
أظهرت أول تجربة ذات شق مزدوج مع شعاع من الإلكترونات، أجراها كلاوس جونسون في ألمانيا عام 1961، أن شعاع الإلكترونات يشكل بالفعل نمط تداخل، مما يعني أن الإلكترونات تتصرف بشكل جماعي كموجة. تم إجراء أول تجارب الشق المزدوج مع إلكترونات مفردة تمر عبر الشقوق واحدة تلو الأخرى بواسطة جوليو بوزي في عام 1974 في إيطاليا وأكيرا تونومورا في عام 1989 في اليابان. وهي تُظهر أن أطراف التداخل تتشكل تدريجيًا، حتى عندما تمر الإلكترونات عبر الشقوق بشكل فردي. يوضح هذا بشكل قاطع أن صور حيود الإلكترون تتشكل بسبب الطبيعة الموجية للإلكترونات. يتم توضيح النتائج التي تظهر في تجارب الشق المزدوج مع الإلكترونات من خلال صور نمط التداخل في الشكل\(\PageIndex{2}\).

في إعداد تجريبي واحد لدراسة أنماط التداخل لموجات الإلكترون، يتم إنشاء شقين في غشاء السيليكون المطلي بالذهب. يبلغ عرض كل شق 62 نانومتر وطوله 4 ميكرومتر، والفصل بين الشقوق هو 272 نانومتر. يتم إنشاء شعاع الإلكترون في مسدس إلكتروني عن طريق تسخين عنصر التنغستن وتسريع الإلكترونات عبر جهد 600 فولت. يتم موازنة الشعاع لاحقًا باستخدام العدسات الكهرومغناطيسية، ويتم إرسال شعاع الإلكترونات الموازي عبر الشقوق. ابحث عن الموضع الزاوي للحافة الساطعة من الدرجة الأولى على شاشة العرض.
إستراتيجية
تذكر أن الموضع الزاوي للحافة الساطعة من الدرجة n التي تكونت في نمط التداخل ذي الشقين الخاص بيونغ (الذي تمت مناقشته في فصل سابق) مرتبط بفصل d بين الشقوق وبالطول الموجي،، للضوء الساقط بالمعادلة dsin = nλ، حيث n = 0،\(\pm 1\)،\(\pm 2\)،... يتم إعطاء الفصل وهو يساوي d = 272 نانومتر. بالنسبة لهامش الدرجة الأولى، نأخذ n = 1. الشيء الوحيد الذي نحتاجه الآن هو الطول الموجي لموجة الإلكترون الساقطة.
نظرًا لأن الإلكترون قد تسارع من السكون عبر فرق محتمل قدره ΔV = 600 فولت، فإن طاقته الحركية هي K = e ΔV = 600 eV. طاقة كتلة الراحة للإلكترون هي\(E_0\) = 511 kEV.
نحسب الطول الموجي لـ de Broglie باعتباره طول موجة إلكترون غير نسبي لأن طاقته الحركية K أصغر بكثير من طاقة الراحة\(E_0\)، K\(E_0\).
الحل
الطول الموجي للإلكترون هو
\[\lambda = \frac{h}{p} = \frac{h}{\sqrt{2m_eK}} = \frac{h}{\sqrt{2E_0/c^2K}} = \frac{hc}{\sqrt{2E_0K}} = \frac{1.241 \times 10^{-6} \, eV \cdot m}{\sqrt{2(511 \, keV)(600 \, eV)}} = 0.050 \, nm. \nonumber \]
يتم استخدام هذا ▼ للحصول على موضع الحافة الساطعة الأولى:
\[\sin \, \theta = \frac{1 \cdot \lambda}{d} = \frac{0.050 \, nm}{272 \, nm} = 0.000184 \Rightarrow θ = 0.010°. \nonumber \]
الدلالة
لاحظ أن هذه هي أيضًا الدقة الزاوية بين طرفين ساطعين متتاليين حتى حوالي n = 1000. على سبيل المثال، بين هامش الترتيب الصفري وهامش الدرجة الأولى، بين هامش الدرجة الأولى والمرتبة الثانية
بالنسبة للحالة الموضحة في المثال\(\PageIndex{1}\)، ابحث عن الموضع الزاوي للهامش الساطع من الدرجة الخامسة على شاشة العرض.
- إجابة
-
\(0.052^o\)
تعد الطبيعة المزدوجة للجسيمات الموجية لجسيمات المادة والإشعاع إعلانًا عن عدم قدرتنا على وصف الواقع المادي ضمن نظرية كلاسيكية موحدة لأنه لا يمكن لمقاربة الجسيمات الكلاسيكية ولا نهج الموجة الكلاسيكية تفسير الظواهر المرصودة بشكل كامل. تم تحقيق هذا القيد في النهج الكلاسيكي بحلول عام 1928، وتم وضع الأساس لنظرية إحصائية جديدة، تسمى ميكانيكا الكم، من قبل بوهر وإدوين شرودنغر وفيرنر هايزنبرغ وبول ديراك. تأخذ ميكانيكا الكم فكرة de Broglie عن موجات المادة باعتبارها الخاصية الأساسية لجميع الجسيمات وتعطيها تفسيرًا إحصائيًا. وفقًا لهذا التفسير، تحمل الموجة المرتبطة بالجسيم معلومات حول المواضع المحتملة للجسيم وعن خصائصه الأخرى. يُنظر إلى الجسيم الواحد على أنه حزمة موجة متحركة مثل تلك الموضحة في الشكل\(\PageIndex{3}\). يمكننا أن نشعر بشكل بديهي من هذا المثال أنه إذا كان الجسيم عبارة عن حزمة موجة، فلن نتمكن من قياس موضعه الدقيق بنفس المعنى حيث لا يمكننا تحديد موقع حزمة الموجة في سلسلة جيتار مهتزة. يرتبط عدم اليقين، Δx، في قياس موضع الجسيم بعدم اليقين، Δp، في القياس المتزامن لزخمه الخطي من خلال مبدأ عدم اليقين لهايزنبرغ:
\[\Delta x \Delta p \geq \frac{1}{2}\hbar. \label{6.63} \]
يعبر مبدأ هايزنبرغ عن قانون الطبيعة الذي يعتبر تصورنا محدودًا على المستوى الكمي. على سبيل المثال، إذا عرفنا الموضع الدقيق للجسم (مما يعني أن Δx = 0 في المعادلة\ ref {6.63}) في نفس الوقت لا يمكننا معرفة زخمه، لأن عدم اليقين في زخمه يصبح غير محدود (لأن Δp ≥ 0.5 /Δx في المعادلة\ ref {6.63}). يحدد مبدأ عدم اليقين في Heisenberg الحد الأقصى لدقة القياسات المتزامنة لموضع وزخم الجسيم؛ يُظهر أن أفضل دقة يمكننا الحصول عليها هي عندما تكون لدينا علامة تساوي (=) في المعادلة\ ref {6.63}، ولا يمكننا أن نفعل أفضل من ذلك، حتى مع الأفضل أدوات المستقبل. مبدأ هايزنبرغ هو نتيجة للطبيعة الموجية للجسيمات.

نحن نستخدم بشكل روتيني العديد من الأجهزة الإلكترونية التي تستغل ازدواجية الجسيمات الموجية دون أن ندرك حتى تطور الفيزياء الكامنة وراء تشغيلها. أحد الأمثلة على التكنولوجيا القائمة على خصائص الجسيمات للفوتونات والإلكترونات هو الجهاز المقترن بالشحن، والذي يستخدم للكشف عن الضوء في أي جهاز يتطلب بيانات رقمية عالية الجودة، كما هو الحال في الكاميرات الرقمية أو في أجهزة الاستشعار الطبية. والمثال الذي يتم فيه استغلال خصائص موجة الإلكترونات هو المجهر الإلكتروني.
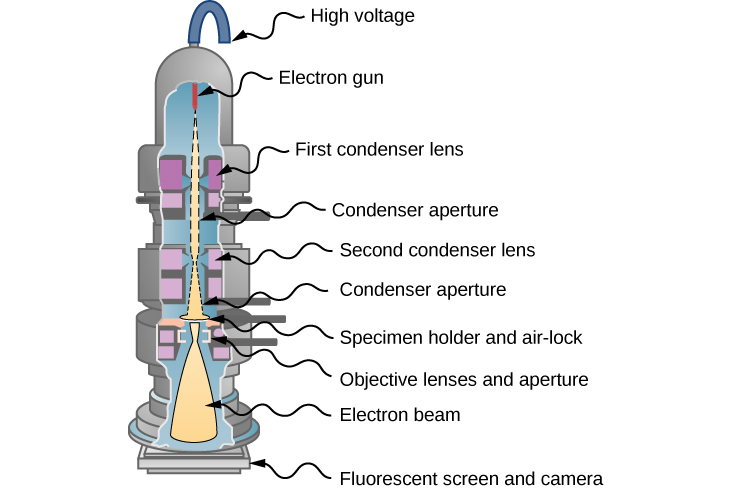
في عام 1931، قام الفيزيائي إرنست روسكا - بناءً على فكرة أن المجالات المغناطيسية يمكنها توجيه شعاع إلكتروني تمامًا كما يمكن للعدسات توجيه شعاع من الضوء في المجهر الضوئي - بتطوير أول نموذج أولي من المجهر الإلكتروني. نشأ هذا التطور في مجال الفحص المجهري الإلكتروني. في المجهر الإلكتروني للإرسال (TEM)، الموضح في الشكل\(\PageIndex{4}\)، يتم إنتاج الإلكترونات بواسطة عنصر التنغستن الساخن ويتم تسريعها من خلال فرق محتمل في مسدس الإلكترون، مما يمنحها ما يصل إلى 400 كيلو فولت من الطاقة الحركية. بعد مغادرة مسدس الإلكترون، يتم تركيز شعاع الإلكترون بواسطة العدسات الكهرومغناطيسية (نظام عدسات التكثيف) ويتم نقله من خلال عينة عينة ليتم عرضها. يتم إعادة بناء صورة العينة من شعاع الإلكترون المرسل. يمكن عرض الصورة المكبرة إما مباشرة على شاشة الفلورسنت أو بشكل غير مباشر عن طريق إرسالها، على سبيل المثال، إلى كاميرا رقمية أو شاشة كمبيوتر. يتم وضع الإعداد الكامل الذي يتكون من مسدس الإلكترون والعدسات والعينة وشاشة الفلورسنت في غرفة تفريغ لمنع فقدان الطاقة من الشعاع. دقة TEM محدودة فقط بالانحراف الكروي (تمت مناقشته في الفصل السابق). يمكن أن تتمتع النماذج الحديثة عالية الدقة من TEM بقدرة حل أكبر من 0.5 ومكبرات أعلى من 50 مليون مرة. للمقارنة، فإن أفضل قدرة حل تم الحصول عليها باستخدام الفحص المجهري الضوئي تبلغ حاليًا حوالي 97 نانومتر. يتمثل أحد قيود TEM في أن العينات يجب أن تكون بسمك حوالي 100 نانومتر وتتطلب العينات البيولوجية تحضيرًا خاصًا يتضمن «تثبيتًا» كيميائيًا لتثبيتها من أجل تقطيعها إلى شرائح رقيقة جدًا.
لا تظهر مثل هذه القيود في مجهر المسح الإلكتروني (SEM)، الذي اخترعه مانفريد فون أردين في عام 1937. في SEM، تصل الطاقة النموذجية لشعاع الإلكترون إلى 40 كيلو فولت ولا تنتقل الحزمة من خلال عينة ولكنها مبعثرة عن سطحها. تتم إعادة بناء الطوبوغرافيا السطحية للعينة من خلال تحليل الإلكترونات المتناثرة في الخلف والإلكترونات المرسلة والإشعاع المنبعث الناتج عن تفاعل الإلكترونات مع الذرات في العينة. قوة حل SEM أفضل من 1 نانومتر، ويمكن أن يكون التكبير أفضل بأكثر من 250 مرة من ذلك الذي تم الحصول عليه باستخدام المجهر الضوئي. يمكن أن تصل العينات الممسوحة ضوئيًا بواسطة SEM إلى عدة سنتيمترات ولكن يجب إعدادها خصيصًا، اعتمادًا على الخصائص الكهربائية للعينة.
تسمح لنا عمليات التكبير العالية لـ TEM و SEM برؤية الجزيئات الفردية. تسمح لنا قوى التحليل العالية لـ TEM و SEM برؤية التفاصيل الدقيقة، مثل تلك الموضحة في صورة SEM المجهرية لحبوب اللقاح في بداية هذا الفصل (الشكل 6.1.1).
إذا مر شعاع إلكتروني طوله ١٫٠ بيومترًا من TEM عبر فتحة دائرية مقدارها ٢٫٠ ميكرومتر، فما الزاوية بين مصدري النقاط القابلين للحل في هذا المجهر؟
الحل
يمكننا استخدام صيغة مباشرة لقوة التحليل\(Δθ\)، الخاصة بالمجهر عندما يكون الطول الموجي للإشعاع\(λ=1.0\, pm\) الساقط وقطر الفتحة هو\(D = 2.0\, μm\):
\[\Delta \theta = 1.22 \frac{\lambda}{D} = 1.22 \frac{1.0 \, pm}{2.0 \, \mu m} = 6.10 \times 10^{-7} rad = 3.50 \times 10.5^o. \nonumber \]
الدلالة
لاحظ أنه إذا استخدمنا مجهرًا تقليديًا بضوء 400 نانومتر، فستكون قوة التحليل 14 درجة فقط، مما يعني أن جميع التفاصيل الدقيقة في الصورة ستكون غير واضحة.
لنفترض أن قطر الفتحة في المثال\(\PageIndex{2}\) قد انخفض إلى النصف. كيف تؤثر على قوة الحل؟
- إجابة
-
يضاعف ذلك


