1.E: طبيعة الضوء (تمارين)
- Page ID
- 196659
أسئلة مفاهيمية
1.1 انتشار الضوء
1. تحت أي ظروف يمكن تصميم الضوء مثل الشعاع؟ مثل الموجة؟
2. لماذا يكون معامل الانكسار دائمًا أكبر من أو يساوي 1؟
3. هل حقيقة وصول وميض الضوء من البرق إليك قبل صوته تثبت أن سرعة الضوء كبيرة للغاية أم أنها ببساطة أكبر من سرعة الصوت؟ ناقش كيف يمكنك استخدام هذا التأثير للحصول على تقدير لسرعة الضوء.
4. تكهن بشأن العملية الفيزيائية التي قد تكون مسؤولة عن انتقال الضوء بشكل أبطأ في الوسط منه في الفراغ.
1.2 قانون التفكير
5. باستخدام قانون الانعكاس، اشرح كيف يزيل المسحوق لمعان أنف الشخص. ما اسم التأثير البصري؟
1.3 الانكسار
6. تم وصف الانتشار بالانعكاس من سطح خشن في هذا الفصل. يمكن أيضًا نشر الضوء عن طريق الانكسار. وصف كيفية حدوث ذلك في موقف معين، مثل تفاعل الضوء مع الثلج المجروش.
7. هل سيغير الضوء اتجاهه نحو العمودي أو بعيدًا عنه عندما ينتقل من الهواء إلى الماء؟ الماء إلى الزجاج؟ من الزجاج إلى الهواء؟
8. اشرح لماذا يبدو جسم ما في الماء دائمًا على عمق أكثر ضحالة مما هو عليه بالفعل؟
9. اشرح لماذا تبدو أرجل الشخص قصيرة جدًا عند الخوض في حمام السباحة. برر تفسيرك بمخطط شعاعي يوضح مسار الأشعة من القدمين إلى عين المراقب الذي خرج من الماء.
10. اشرح لماذا يبدو المجذاف المغمور جزئيًا في الماء منحنيًا.
1.4 الانعكاس الداخلي الكلي
11. يتم إسقاط خاتم به حجر كريم عديم اللون في الماء. تصبح الأحجار الكريمة غير مرئية عند غمرها. هل يمكن أن تكون ماسة؟ اشرح.
12. النوع الأكثر شيوعًا من السراب هو الوهم بأن الضوء المنبعث من الأجسام البعيدة ينعكس في بركة مياه غير موجودة بالفعل. يُلاحظ السراب عمومًا في الصحاري، عندما تكون هناك طبقة ساخنة من الهواء بالقرب من الأرض. إذا كان معامل انكسار الهواء أقل بالنسبة للهواء في درجات الحرارة المرتفعة، اشرح كيف يمكن تكوين السراب.
13. كيف يمكنك استخدام الانعكاس الداخلي الكلي لتقدير معامل انكسار الوسط؟
1.5 التشتت
14. هل من الممكن أن يلعب الانعكاس الداخلي الكلي دورًا في أقواس قزح؟ اشرح من حيث مؤشرات الانكسار والزوايا، ربما بالرجوع إلى ما هو موضح أدناه. لقد شهد البعض منا تشكيل قوس قزح مزدوج؛ هل من الممكن فعليًا مشاهدة قوس قزح ثلاثي؟ صورة لقوس قزح مزدوج.

15. قد يكون الماس عالي الجودة واضحًا تمامًا وعديم اللون، حيث ينقل جميع الأطوال الموجية المرئية مع القليل من الامتصاص. اشرح كيف يمكن أن تتألق مع ومضات ذات ألوان زاهية عند إضاءتها بالضوء الأبيض.
1.6 مبدأ هيغنز
16. كيف تعتمد تأثيرات الموجة على حجم الكائن الذي تتفاعل معه الموجة؟ على سبيل المثال، لماذا ينحني الصوت حول زاوية المبنى بينما لا ينحني الضوء؟
17. هل ينطبق مبدأ Huygens على جميع أنواع الموجات؟
18. إذا لوحظ الانحراف لبعض الظواهر، فهذا دليل على أن الظاهرة هي موجة. هل العكس صحيح؟ أي إذا لم يتم ملاحظة الحيود، فهل يعني ذلك أن الظاهرة ليست موجة؟
1.7 الاستقطاب
19. هل يمكن استقطاب موجة صوتية في الهواء؟ اشرح.
20. لا يمر أي ضوء من خلال مرشحين استقطابيين مثاليين بمحاور عمودية. ومع ذلك، إذا تم وضع مرشح استقطابي ثالث بين الإصدارين الأصليين، فقد يمر بعض الضوء. لماذا هذا؟ تحت أي ظروف يمر معظم الضوء؟
21. اشرح ما يحدث للطاقة التي يحملها الضوء والتي يتم تعتيمها عن طريق تمريرها عبر مرشحين استقطابيين متقاطعين.
22. عندما تكون الجسيمات التي تشتت الضوء أصغر بكثير من طوله الموجي، فإن مقدار التشتت يتناسب مع\(\displaystyle \frac{1}{λ}\). هل هذا يعني أن هناك المزيد من التشتت للصغار\(\displaystyle λ\) من الكبار\(\displaystyle λ\)؟ كيف يرتبط هذا بحقيقة أن السماء زرقاء؟
23. باستخدام المعلومات الواردة في السؤال السابق، اشرح سبب ظهور غروب الشمس باللون الأحمر.
24. عندما ينعكس الضوء بزاوية بروستر من سطح أملس، يتم\(\displaystyle 100%\) استقطابه بالتوازي مع السطح. سينكسر جزء من الضوء في السطح. وصف كيفية إجراء تجربة لتحديد استقطاب الضوء المنكسر. ما هو الاتجاه الذي تتوقع أن يتخذه الاستقطاب وهل تتوقع أن يكون\(\displaystyle 100%\)؟
25. إذا كنت مستلقيًا على الشاطئ وتنظر إلى الماء ورأسك يميل جانبًا قليلاً، فإن النظارات الشمسية المستقطبة لا تعمل جيدًا. لماذا لا؟
مشاكل
1.1 انتشار الضوء
26. ما سرعة الضوء في الماء؟ في الغليسيرين؟
27. ما سرعة الضوء في الهواء؟ في زجاج التاج؟
28. احسب معامل الانكسار لوسيط تكون فيه سرعة الضوء\(\displaystyle 2.012×10^8m/s\)، وحدِّد المادة الأكثر احتمالاً استنادًا إلى الجدول 1.1.
29. في أي مادة في الجدول 1.1 تمثل سرعة الضوء\(\displaystyle 2.290×10^8m/s\)؟
30. كان هناك تصادم كبير لكويكب مع القمر في العصور الوسطى. وقد وصفها الرهبان في كاتدرائية كانتربري في إنجلترا بأنها توهج أحمر على القمر وحوله. ما المدة التي سيستغرقها الكويكب بعد ارتطام الكويكب بالقمر\(\displaystyle 3.84×10^5km\) البعيد، هل سيصل الضوء أولاً إلى الأرض؟
31. تتواصل مكونات بعض أجهزة الكمبيوتر مع بعضها البعض من خلال الألياف الضوئية ذات معامل الانكسار\(\displaystyle n=1.55\). ما الوقت بالنانو ثانية اللازم للإشارة للانتقال لمسافة 0.200 متر عبر هذه الألياف؟
32. قارن الوقت الذي يستغرقه الضوء لقطع 1000 متر على سطح الأرض وفي الفضاء الخارجي.
33. إلى أي مدى ينتقل الضوء تحت الماء خلال فترة زمنية تبلغ\(\displaystyle 1.50×10^{−6}s\)؟
1.2 قانون التفكير
34. لنفترض أن الرجل يقف أمام المرآة كما هو موضح أدناه. يبلغ ارتفاع عيناه 1.65 مترًا فوق الأرض وأعلى رأسه 0.13 مترًا. ابحث عن الارتفاع فوق أرضية أعلى وأسفل أصغر مرآة يمكنه من خلالها رؤية قمة رأسه وقدميه. كيف ترتبط هذه المسافة بارتفاع الرجل؟
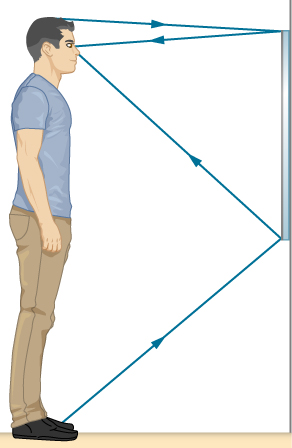
هذا الشكل عبارة عن رسم لرجل يقف أمام المرآة وينظر إلى صورته. يبلغ طول المرآة حوالي نصف طول الرجل، وأعلى المرآة فوق عينيه ولكن تحت قمة رأسه. تصل أشعة الضوء من قدميه إلى أسفل المرآة وتنعكس على عينيه. تصل الأشعة من أعلى رأسه إلى قمة المرآة وتنعكس على عينيه.
35. أظهر أنه عندما ينعكس الضوء من مرآتين تتقابلان بزاوية قائمة، يكون الشعاع الصادر موازيًا للشعاع الوارد، كما هو موضح أدناه.
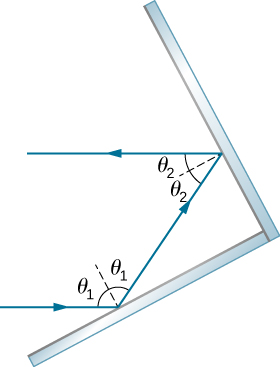
تلتقي مرآتان مع بعضهما البعض بزاوية قائمة. يصطدم شعاع الضوء الوارد بمرآة واحدة بزاوية ثيتا واحدة إلى وضعها الطبيعي، وينعكس في نفس زاوية ثيتا على الجانب الآخر من المعتاد، ثم يضرب المرآة الأخرى بزاوية ثيتا اثنين إلى الزاوية العادية وينعكس في نفس زاوية ثيتا اثنين على الجانب الآخر من الوضع الطبيعي، بحيث الشعاع الصادر موازٍ للشعاع الوارد.
36. على سطح القمر، وضع رواد الفضاء القمريون عاكسًا للزاوية، ينعكس عليه شعاع الليزر بشكل دوري. يتم حساب المسافة إلى القمر من وقت الذهاب والعودة. ما النسبة المئوية للتصحيح المطلوب لتفسير التأخير الزمني بسبب تباطؤ الضوء في الغلاف الجوي للأرض؟ افترض أن المسافة إلى القمر دقيقة\(\displaystyle 3.84×10^8m\) وأن الغلاف الجوي للأرض (الذي يختلف في الكثافة مع الارتفاع) يعادل طبقة يبلغ سمكها 30.0 كم مع معامل انكسار ثابت\(\displaystyle n=1.000293\).
37. المرآة المسطحة لا تتقارب ولا تتباعد. ولإثبات ذلك، ضع في اعتبارك شعاعين ينبعان من نفس النقطة ويختلفان بزاوية\(\displaystyle θ\) (انظر أدناه). أظهر أنه بعد الاصطدام بمرآة الطائرة، تبقى الزاوية بين اتجاهاتهما\(\displaystyle θ\).
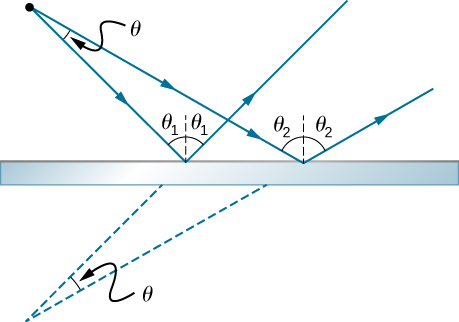
تسقط أشعة الضوء المتباينة من نقطة بزاوية ثيتا على مرآة في مكانين مختلفين وتتباعد أشعتها المنعكسة. يصطدم شعاع واحد بزاوية واحدة من الزاوية العادية، وينعكس في نفس الزاوية التي يعكسها شعاع واحد على الجانب الآخر من الشعاع. ويصطدم الشعاع الآخر بزاوية أكبر بمقدار درجتين من العادي، وينعكس في نفس الزاوية بمقدار درجتين على الجانب الآخر من المستقيم. عندما تمتد الأشعة المنعكسة للخلف من نقاط انعكاسها، فإنها تلتقي عند نقطة خلف المرآة، في نفس الزاوية التي تركت بها المصدر.
1.3 الانكسار
ما لم يتم تحديد خلاف ذلك، بالنسبة للمشاكل من 1 إلى 10، يجب اعتبار مؤشري انكسار الزجاج والماء 1.50 و 1.333 على التوالي.
38. شعاع الضوء في الهواء له زاوية سقوط\(\displaystyle 35°\) على سطح لوح زجاجي. ما زاويتا الانعكاس والانكسار؟
39. يسقط شعاع ضوئي في الهواء على سطح البركة، مما يجعل الزاوية\(\displaystyle 20°\) 20 درجة بالنسبة للسطح. ما زاويتا الانعكاس والانكسار؟
40. عندما ينتقل شعاع الضوء من الماء إلى الزجاج، فإنه يظهر\(\displaystyle 30°\) بزاوية تتعلق بالوضع الطبيعي للواجهة. ما زاوية الإصابة به؟
41. يرسل مصباح قلم رصاص مغمور في الماء شعاعًا ضوئيًا نحو السطح بزاوية سقوط قدرها\(\displaystyle 30°\). ما زاوية الانكسار في الهواء؟
42. تشكل أشعة الضوء الصادرة من الشمس\(\displaystyle 30°\) زاوية إلى الوضع الرأسي عند رؤيتها من تحت سطح جسم مائي. في أي زاوية فوق الأفق توجد الشمس؟
43. ينتقل مسار شعاع الضوء في الهواء من زاوية السقوط\(\displaystyle 35°\) إلى زاوية الانكسار\(\displaystyle 22°\) عند دخوله كتلة مستطيلة من البلاستيك. ما معامل انكسار البلاستيك؟
44. ينظر الغواص الذي يتدرب في حمام السباحة إلى مدربه كما هو موضح أدناه. ما الزاوية التي يصنعها الشعاع الصادر من وجه المعلم مع العمود العمودي على الماء عند النقطة التي يدخل منها الشعاع؟ الزاوية بين الشعاع في الماء والعمودي على الماء هي\(\displaystyle 25.0°\).
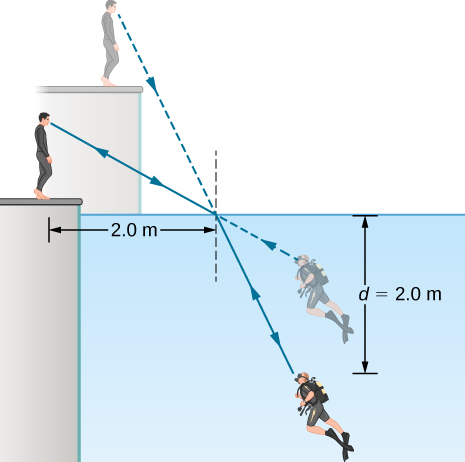
ينظر غواص السكوبا ومدربه إلى بعضهما البعض. يرون بعضهم البعض في المواقع التي يتم الحصول عليها من خلال استقراء الخط المستقيم للأشعة التي تصل إلى أعينهم. بالنسبة للمدرب، يبدو الغواص أقل عمقًا مما هو عليه بالفعل، وبالنسبة للغواص، يبدو المدرب أعلى مما هو عليه بالفعل. بالنسبة للمدرب، تبدو أقدام الغواص على عمق نقطتين صفرًا من الأمتار. يصطدم الشعاع الساقط من المدرب بسطح الماء على مسافة أفقية تبلغ نقطتين صفرًا من المدرب. رأس الغواص هو مسافة رأسية قدرها d تساوي نقطتين صفريتين تحت سطح الماء.
45. (أ) باستخدام المعلومات الواردة في المشكلة السابقة، ابحث عن ارتفاع رأس المدرب فوق الماء، مع ملاحظة أنه سيتعين عليك أولاً حساب زاوية السقوط.
(ب) ابحث عن العمق الظاهر لرأس الغواص تحت الماء كما يراه المدرب.
1.4 الانعكاس الداخلي الكلي
46. تحقق من أن الزاوية الحرجة للضوء المنتقل من الماء إلى الهواء\(\displaystyle 48.6°\)، كما تمت مناقشته في نهاية المثال 1.4، تتعلق بالزاوية الحرجة للضوء الذي ينتقل في أنبوب البوليسترين (نوع من البلاستيك) المحاط بالهواء.
47. (أ) في نهاية المثال 1.4، ذُكر أن الزاوية الحرجة للضوء المنتقل من الماس إلى الهواء هي\(\displaystyle 24.4°\). تحقق من ذلك.
(ب) ما الزاوية الحرجة للضوء المنتقل من الزركون إلى الهواء؟
48. تستخدم الألياف الضوئية زجاج الصوان المغطى بزجاج التاج. ما الزاوية الحرجة؟
49. ما هي الزاوية الدنيا التي ستحصل بها على انعكاس داخلي كلي للضوء المنتقل في الماء وينعكس من الجليد؟
50. لنفترض أنك تستخدم الانعكاس الداخلي الكلي لإنشاء عاكس زاوية فعال. إذا كان هناك هواء بالخارج وزاوية السقوط هي زاوية السقوط\(\displaystyle 45.0°\)، فما الحد الأدنى لمؤشر انكسار المادة التي صُنع منها العاكس؟
51. يمكنك تحديد معامل انكسار مادة من خلال تحديد الزاوية الحرجة لها.
(أ) ما معامل انكسار مادة لها زاوية حرجة\(\displaystyle 68.4°\) عند غمرها في الماء؟ ما هي المادة، بناءً على الجدول 1.1؟
(ب) ما هي الزاوية الحرجة لهذه المادة في الهواء؟
52. يخضع شعاع الضوء، المنبعث تحت سطح سائل غير معروف مع الهواء فوقه، لانعكاس داخلي كامل كما هو موضح أدناه. ما معامل انكسار السائل وتحديده المحتمل؟
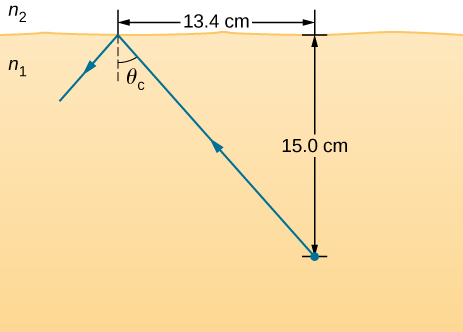
ينتقل شعاع ضوئي من جسم وُضع في وسط n 1 عند 15.0 سنتيمترًا أسفل الواجهة الأفقية مع وسيط n 2. ينعكس هذا الشعاع داخليًا تمامًا باستخدام theta c كزاوية حرجة. المسافة الأفقية بين الجسم ونقطة الإصابة هي 13.4 سم.
53. تسقط أشعة الضوء بشكل طبيعي على السطح الرأسي للمنشور الزجاجي (\(\displaystyle n=1.50\)كما هو موضح أدناه).
(أ) ما هي أكبر قيمة بحيث ينعكس الشعاع بالكامل على الوجه المائل؟\(\displaystyle ϕ\)
(ب) كرر حساب الجزء (أ) إذا كان المنشور مغمورًا في الماء.
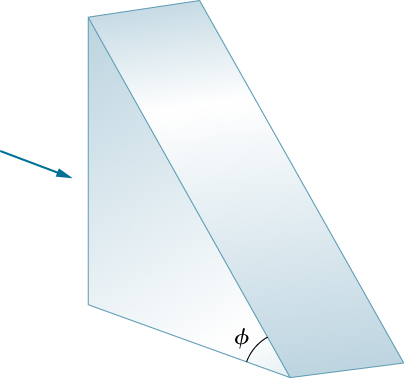
يحتوي المنشور الثلاثي ذو الزاوية اليمنى على قاعدة أفقية وجانب عمودي. يصنع وتر المثلث زاوية phi مع القاعدة الأفقية. تسقط أشعة الضوء الأفقية بشكل طبيعي على السطح الرأسي للمنشور.
1.5 التشتت
54. (أ) ما نسبة سرعة الضوء الأحمر إلى الضوء البنفسجي في الماس، استناداً إلى الجدول 1.2؟
(ب) ما هي هذه النسبة في البوليستيرين؟
(ج) أيهما أكثر تشتتًا؟
55. ينتقل شعاع الضوء الأبيض من الهواء إلى الماء بزاوية سقوط تبلغ\(\displaystyle 75.0°\). ما قياس زاوية انكسار أجزاء الضوء الحمراء (660 nm) والبنفسجية (410 nm) من الضوء؟
56. ما مقدار اختلاف الزوايا الحرجة للضوء الأحمر (660 نانومتر) والبنفسجي (410 نانومتر) في الماس المُحاط بالهواء؟
57. (أ) ينتقل شعاع ضيق من الضوء يحتوي على أطوال موجية صفراء (580 نانومترية) وأخضر (550 نانومتر) من البوليستيرين إلى الهواء، فيصطدم بالسطح\(\displaystyle 30.0°\) بزاوية سقوط. ما الزاوية بين الألوان عند ظهورها؟
(ب) إلى أي مدى سيتعين عليهم السفر حتى يفصل بينهم كيلومتر واحد؟
58. ينتقل شعاع متوازي من الضوء يحتوي على أطوال موجية برتقالية (610 نانومتر) وبنفسجية (410 نانومتر) من الكوارتز المنصهر إلى الماء، فيصطدم بالسطح بينهما\(\displaystyle 60.0°\) بزاوية سقوط. ما الزاوية بين اللونين في الماء؟
59. ينتقل شعاع من ضوء 610 نانومتر من الهواء إلى الكوارتز المنصهر بزاوية سقوط تبلغ\(\displaystyle 55.0°\). عند أي زاوية سقوط يجب أن يدخل ضوء ٤٧٠ نانومترًا زجاج الصوان للحصول على نفس زاوية الانكسار؟
60. ينتقل شعاع ضيق من الضوء يحتوي على أطوال موجية باللونين الأحمر (660 نانومتر) والأزرق (470 نانومتر) من الهواء عبر قطعة مسطحة من زجاج التاج بسمك 1.00 سم ويعود إلى الهواء مرة أخرى. يضرب\(\displaystyle 30.0°\) الشعاع بزاوية السقوط.
(أ) في أي زوايا يظهر اللونان؟
(ب) ما المسافة التي يفصل بها اللون الأحمر عن اللون الأزرق عند ظهورهما؟
61. يدخل شعاع ضيق من الضوء الأبيض إلى منشور مصنوع من زجاج التاج بزاوية سقوط\(\displaystyle 45.0°\)، كما هو موضح أدناه. في أي زاوية تخرج مكوّنات الضوء الحمراء (660 نانومتر) والبنفسجية (410 نانومتر) من المنشور؟\(\displaystyle θ_R\)\(\displaystyle θ_V\)
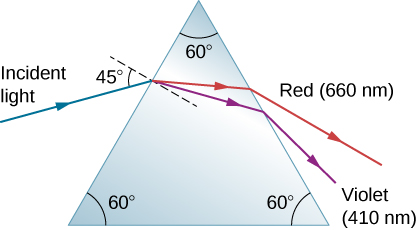
يسقط شعاع ضوئي أزرق بزاوية سقوط تساوي 45 درجة للزاوية العادية على منشور مثلث متساوي الأضلاع تكون جميع أركانه بزوايا تساوي 60 درجة. عند السطح الأول، ينكسر الشعاع وينقسم إلى أشعة حمراء وبنفسجية. تصطدم هذه الأشعة بالسطح الثاني وتخرج من المنشور. ينحني الضوء الأحمر الذي يبلغ 660 نانومترًا أقل من الضوء البنفسجي بـ 410 نانومتر.
1.7 الاستقطاب
62. ما الزاوية اللازمة بين اتجاه الضوء المستقطب ومحور المرشح المستقطب لخفض شدته إلى النصف؟
63. الزاوية بين محاور مرشحي الاستقطاب هي\(\displaystyle 45.0°\). ما مقدار ما يقلل الفلتر الثاني من شدة الضوء القادم من الأول؟
64. \(\displaystyle P_1\)ورقتان مستقطبتان\(\displaystyle P_2\) ويتم وضعهما معًا مع محاور الإرسال الموجهة بزاوية\(\displaystyle θ\) لبعضهما البعض. ماذا يحدث\(\displaystyle θ\) عندما تمر فقط\(\displaystyle 25%\) من الحد الأقصى لشدة الضوء المرسلة من خلالها؟
65. لنفترض أنه في المشكلة السابقة كان الضوء الساقط\(\displaystyle P_1\) غير مستقطب. ما الكسر الذي يمر عبر المجموعة من الضوء الساقط بالقيمة المحدَّدة؟\(\displaystyle θ\)
66. إذا كان لديك ضوء مستقطب تمامًا بكثافة\(\displaystyle 150W/m^2\)، فماذا ستكون شدته بعد المرور عبر مرشح استقطابي بحيث يكون محوره\(\displaystyle 89.0°\) بزاوية تصل إلى اتجاه استقطاب الضوء؟
67. ما الزاوية التي يحتاج محور المرشح المستقطب إلى تكوينها في اتجاه شدة الضوء المستقطب\(\displaystyle 1.00kW/m^2\) لتقليل الكثافة إليها\(\displaystyle 10.0W/m^2\)؟
68. في نهاية المثال 1.7، ذُكر أن شدة الضوء المستقطب تنخفض إلى\(\displaystyle 90.0%\) قيمته الأصلية بالمرور عبر مرشح استقطابي مع محوره بزاوية اتجاه الاستقطاب.\(\displaystyle 18.4°\) تحقق من صحة هذا البيان.
69. أظهر أنه إذا كان لديك ثلاثة فلاتر مستقطبة،\(\displaystyle 45.0°\) بحيث يكون الثاني بزاوية الأولى والثالث بزاوية الأولى، فإن شدة الضوء الذي يمر به الأول ستنخفض إلى\(\displaystyle 25.0%\) قيمته.\(\displaystyle 90.0°\) (هذا على عكس وجود الأول والثالث فقط، مما يقلل الكثافة إلى الصفر، بحيث يؤدي وضع الثانية بينهما إلى زيادة شدة الضوء المرسل.)
70. يتم وضع ثلاث أوراق مستقطبة معًا بحيث يتم توجيه محور الإرسال للورقة الثانية\(\displaystyle 25.0°\) إلى محور الأولى، بينما يتم توجيه محور الإرسال للورقة الثالثة\(\displaystyle 40.0°\) (بنفس المعنى) إلى محور الأولى. ما مقدار شدة الشعاع غير المستقطب الساقط الذي ينتقل عن طريق التركيبة؟
71. من أجل تدوير محور الاستقطاب لشعاع من الضوء المستقطب خطيًا\(\displaystyle 90.0°\)، يقوم الطالب بوضع الألواح\(\displaystyle P_1\)\(\displaystyle P_2\) ومحاور الإرسال الخاصة بها عند محور الاستقطاب الخاص بالشعاع،\(\displaystyle 45.0°\) وعلى\(\displaystyle 90.0°\) التوالي.
(أ) الجزء من الضوء الساقط الذي يمر من خلاله\(\displaystyle P_1\) و
(ب) من خلال الجمع؟
(ج) كرر حساباتك للجزء (ب) لزوايا محور الإرسال لـ\(\displaystyle 30.0°\) و\(\displaystyle 90.0°\)، على التوالي.
72. وجد أنه عندما يسقط الضوء المنتقل في الماء على كتلة بلاستيكية، تكون زاوية بروستر هي\(\displaystyle 50.0°\). ما معامل انكسار البلاستيك؟
73. في أي زاوية سيكون الضوء المنعكس من الماس مستقطبًا تمامًا؟
74. ما زاوية بروستر للضوء المنتقل في الماء المنعكس من زجاج التاج؟
75. يرى الغواص الضوء المنعكس من سطح الماء. في أي زاوية سيكون هذا الضوء مستقطبًا تمامًا؟
مشاكل إضافية
76. من خلال قياساته، قدّر رومر أن الضوء استغرق 22 دقيقة لقطع مسافة تساوي قطر مدار الأرض حول الشمس.
(أ) استخدم هذا التقدير إلى جانب القطر المعروف لمدار الأرض للحصول على قيمة تقريبية لسرعة الضوء.
(ب) يستغرق الضوء فعليًا 16.5 دقيقة لقطع هذه المسافة. استخدم هذا الوقت لحساب سرعة الضوء.
77. أجرى كورنو قياس Fizeau لسرعة الضوء باستخدام عجلة قطرها 4.00 سم تحتوي على 180 سنًا. كانت المسافة من العجلة إلى المرآة 22.9 كم. بافتراض أنه قام بقياس سرعة الضوء بدقة، فما السرعة الزاوية للعجلة؟
78. لنفترض أن لديك مادة صافية غير معروفة مغمورة في الماء، وترغب في التعرف عليها من خلال إيجاد معامل الانكسار. تقوم بالترتيب لإدخال شعاع من الضوء إليه بزاوية مقدارها\(\displaystyle 45.0°\)، وتراقب زاوية الانكسار\(\displaystyle 40.3°\). ما معامل انكسار المادة وهويتها المحتملة؟
79. يظهر أدناه شعاع من الضوء ينتقل من الهواء عبر زجاج التاج إلى الماء، مثل الذهاب إلى حوض أسماك. احسب مقدار إزاحة الشعاع بواسطة الزجاج\(\displaystyle (Δx)\)، علمًا أن زاوية السقوط تساوي تساوي\(\displaystyle 40.0°\) سُمك الزجاج ١٫٠٠ سم.
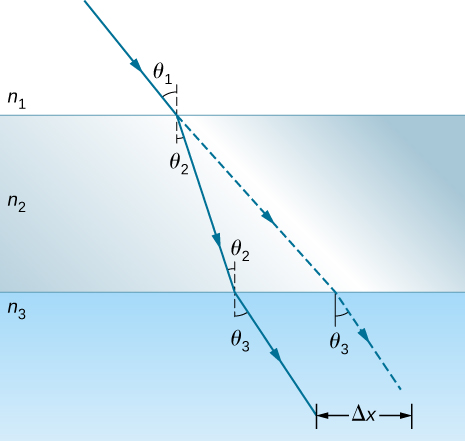
يوضح الشكل الانكسار الذي يحدث عندما ينتقل الضوء من متوسط\(\displaystyle n_1\) إلى\(\displaystyle n_3\) وسط متوسط\(\displaystyle n_2\). يصنع الشعاع الساقط زاوية\(\displaystyle θ_1\) برسم عمودي عند نقطة السقوط عند الواجهة بين\(\displaystyle n_1\) و\(\displaystyle n_2\). \(\displaystyle n_2\)ينحني شعاع الضوء الداخل نحو الخط العمودي مكونًا زاوية\(\displaystyle θ_2\) به على\(\displaystyle n_2\) الجانب. يصل الشعاع إلى الواجهة\(\displaystyle n_2\) بين\(\displaystyle n_3\) زاوية عمودية مرسومة عند نقطة السقوط عند هذه الواجهة، وينحني الشعاع المرسل بعيدًا عن العمودي، مما يجعل زاوية ثيتا ثلاثة على\(\displaystyle n_3\) العمود.\(\displaystyle θ_2\) يظهر استقراء الخط المستقيم للأشعة الساقطة الأصلية كخط منقط. ويتوازي هذا الخط الشعاع المنكسر في الوسط الثالث\(\displaystyle n_3\)، ويتم إزاحته مسافة دلتا x من الشعاع المنكسر. يقع الشعاع المُستقرَأ في نفس الزاوية الثلاثة المتعامدة في الوسط\(\displaystyle n_3\) مثل الشعاع المنكسر.
80. بالنظر إلى المشكلة السابقة، أظهر أنها ستكون\(\displaystyle θ_3\) هي نفسها كما لو لم تكن الوسيلة الثانية موجودة.
81. في أي زاوية يكون الضوء داخل زجاج التاج مستقطبًا تمامًا عند انعكاسه من الماء، كما هو الحال في حوض السمك؟
82. الضوء المنعكس\(\displaystyle 55.6°\) من النافذة مستقطب تمامًا. ما معامل انكسار النافذة والمادة المحتملة التي تُصنع منها؟
83. (أ) الضوء المنعكس\(\displaystyle 62.5°\) من الحجر الكريم في الحلقة مستقطب تمامًا. هل يمكن أن تكون الجوهرة ماسة؟
(ب) في أي زاوية سيكون الضوء مستقطبًا تمامًا إذا كانت الأحجار الكريمة في الماء؟
84. \(\displaystyle θ_b\)إذا كانت زاوية بروستر للضوء المنعكس من أعلى الواجهة بين مادتين،\(\displaystyle θ'_b\) وزاوية بروستر للضوء المنعكس من الأسفل، أثبت ذلك\(\displaystyle θ_b+θ'_b=90.0°\).
85. نتائج غير معقولة لنفترض أن الضوء ينتقل من الماء إلى مادة أخرى بزاوية سقوط\(\displaystyle 10.0°\) وزاوية انكسار قدرها\(\displaystyle 14.9°\).
(أ) ما معامل انكسار المادة الأخرى؟
(ب) ما هو الشيء غير المعقول في هذه النتيجة؟
(ج) ما هي الافتراضات غير المعقولة أو غير المتسقة؟
86. نتائج غير معقولة يضرب الضوء الذي ينتقل من الماء إلى الحجر الكريم السطح بزاوية\(\displaystyle 80.0°\) انكساره بزاوية انكسارها\(\displaystyle 15.2°\).
(أ) ما سرعة الضوء في الحجر الكريم؟
(ب) ما هو الشيء غير المعقول في هذه النتيجة؟
(ج) ما هي الافتراضات غير المعقولة أو غير المتسقة؟
87. إذا كان المرشح المستقطب يقلل من شدة الضوء المستقطب إلى\(\displaystyle 50.0%\) قيمته الأصلية، فما مقدار انخفاض المجالات الكهربائية والمغناطيسية؟
88. لنفترض أنك ارتديت زوجين من النظارات الشمسية المستقطبة بمحاورها بزاوية مقدارها\(\displaystyle 15.0°\). كم من الوقت سيستغرق الضوء لإيداع كمية معينة من الطاقة في عينك مقارنة بزوج واحد من النظارات الشمسية؟ افترض أن العدسات شفافة باستثناء خصائصها الاستقطابية.
89. (أ) في اليوم الذي تكون فيه شدة ضوء الشمس\(\displaystyle 1.00kW/m^2\)، تقوم عدسة دائرية قطرها 0.200 متر بتركيز الضوء على الماء في كوب أسود. يتم وضع لوحين مستقطبين من البلاستيك أمام العدسة مع محاورهما بزاوية\(\displaystyle 20.0°\). بافتراض أن ضوء الشمس غير مستقطب وأن المستقطبات\(\displaystyle 100%\) فعالة، ما هو المعدل الأولي لتسخين الماء\(\displaystyle °C/s\)، بافتراض أنه تم\(\displaystyle 80.0%\) امتصاصه؟ يبلغ وزن كوب الألمنيوم 30.0 جرامًا ويحتوي على 250 جرامًا من الماء.
(ب) هل تسخن المرشحات المستقطبة؟ اشرح.
مشاكل التحدي
90. تستخدم عروض الضوء التي يتم تنظيمها باستخدام الليزر المرايا المتحركة لتأرجح الحزم وإنشاء تأثيرات ملونة. أظهر أن شعاع الضوء المنعكس من المرآة يغير اتجاهه\(\displaystyle 2θ\) عندما يتم تدوير المرآة بزاوية\(\displaystyle θ\).
91. ضع في اعتبارك دخول ضوء الشمس إلى الغلاف الجوي للأرض عند شروق الشمس وغروبها - أي بزاوية السقوط.\(\displaystyle 90.0°\) إذا كان الحد الفاصل بين الفضاء الفارغ تقريبًا والغلاف الجوي مفاجئًا، فاحسب زاوية الانكسار لضوء الشمس. يؤدي هذا إلى إطالة الوقت الذي تبدو فيه الشمس فوق الأفق، عند شروق الشمس وغروبها. الآن قم بتكوين مشكلة تحدد فيها زاوية الانكسار لنماذج مختلفة من الغلاف الجوي، مثل الطبقات المختلفة ذات الكثافة المتغيرة. قد يرغب معلمك في إرشادك بشأن مستوى التعقيد الذي يجب مراعاته وكيفية اختلاف مؤشر الانكسار مع كثافة الهواء.
92. ينكسر شعاع الضوء الذي يدخل الألياف الضوئية المحاطة بالهواء أولاً ثم ينعكس كما هو موضح أدناه. أظهر أنه إذا كانت الألياف مصنوعة من زجاج التاج، فسوف ينعكس أي شعاع ساقط داخليًا تمامًا.
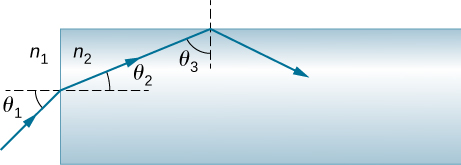
يوضِّح الشكل ضوءًا\(\displaystyle n_1\) ينتقل من الوجه الأيسر لكتلة مستطيلة من المواد ويسقط عليها\(\displaystyle n_2\). يسقط الشعاع بزاوية سقوط\(\displaystyle θ_1\)، ويتم قياسها بالنسبة للمستوى الطبيعي للسطح الذي يدخل منه الشعاع. تكون زاوية الانكسار\(\displaystyle θ_2\)، مرة أخرى، نسبة إلى المستوى الطبيعي للسطح. يسقط الشعاع المنكسر على الوجه العلوي للكتلة وينعكس داخليًا تمامًا بزاوية السقوط.\(\displaystyle θ_3\)
93. يسقط شعاع الضوء على الوجه الأيسر من المنشور (انظر أدناه) بزاوية السقوط التي يكون فيها\(\displaystyle θ\) للشعاع الناشئ زاوية انكسار\(\displaystyle θ\) في الوجه الأيمن. بيّن أن معامل الانكسار n للمنشور الزجاجي يُعطى من خلال\(\displaystyle n=\frac{sin\frac{1}{2}(α+ϕ)}{sin\frac{1}{2}ϕ}\) موضع\(\displaystyle ϕ\) زاوية رأس المنشور،\(\displaystyle α\) وهي الزاوية التي انحرف من خلالها الشعاع. إذا كانت\(\displaystyle α=37.0°\) كل زاوية من زوايا قاعدة المنشور تساوي كل منها\(\displaystyle 50.0°\)، فما قيمة n؟
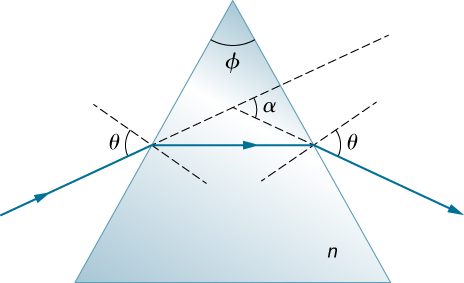
يسقط شعاع ضوئي على الوجه الأيسر لمنشور مثلثي يحتوي رأسه العلوي على زاوية phi ومؤشر انكساره هو n، وزاوية سقوط الشعاع بالنسبة إلى العادي على الوجه الأيسر هي ثيتا. ينكسر الشعاع في المنشور. الشعاع المنكسر أفقي، موازٍ لقاعدة المنشور. يصل الشعاع المنكسر إلى الوجه الأيمن للمنشور وينكسر عند خروجه من المنشور. يصنع الشعاع الناشئ زاوية الثيتا بحيث يكون الوجه الطبيعي على الوجه الأيمن.
94. إذا كانت زاوية\(\displaystyle ϕ\) الذروة في المشكلة السابقة هي\(\displaystyle 20.0°\) و\(\displaystyle n=1.50\)، فما قيمة\(\displaystyle α\)؟
95. \(\displaystyle P_1\)يتم استقطاب الضوء الساقط على الورقة المستقطبة خطيًا بزاوية تتعلق\(\displaystyle 30.0°\) بمحور الإرسال لـ\(\displaystyle P_1\). \(\displaystyle P_2\)يتم وضع الورقة بحيث يكون محورها موازيًا لمحور الاستقطاب للضوء الساقط، أي أيضًا\(\displaystyle 30.0°\) فيما يتعلق بـ\(\displaystyle P_1\).
(أ) ما هو الجزء من الضوء الساقط الذي يمر\(\displaystyle P_1\)؟
(ب) ما هو جزء الضوء الساقط الذي تمر به التركيبة؟
(ج) عن طريق الدوران\(\displaystyle P_2\)، يتم الحصول على الحد الأقصى لكثافة الإرسال. ما نسبة هذه الكثافة القصوى إلى شدة الضوء المرسل عندما يتعلق الأمر\(\displaystyle P_2\)\(\displaystyle 30.0°\) بـ AT\(\displaystyle P_1\)؟
96. أثبت أنه إذا كانت I هي شدة الضوء المنقول بواسطة مرشحين مستقطبين بمحاور بزاوية\(\displaystyle θ\) وكانت\(\displaystyle I'\) الكثافة عندما تكون المحاور بزاوية\(\displaystyle 90.0°−θ\)\(\displaystyle I+I'=I_0\)، فإن الكثافة الأصلية هي. (تلميح: استخدم الهويات المثلثية\(\displaystyle cos90.0°−θ=sinθ\) و\(\displaystyle cos^2θ+sin^2θ=1\).)


