Skip to main content
Global

10.3: عدم المساواة العقلانية

  1. Last updated
  2. Save as PDF
  • Page ID
    167182

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    يتضمن حل المتباينات النسبية إيجاد أصفار البسط والمقام، ثم استخدام هذه القيم للبحث في مناطق مجموعة الحلول على خط الأعداد.

    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/10:_عدم_المساواة/10.03:_عدم_المساواة_العقلانية), /content/body/section[1]/header/div/h5/span/span, line 1, column 17

    حل عدم المساواة واكتب مجموعات الحلول بتدوين الفاصل الزمني:

    1. \(\dfrac{x − 1}{x + 1} ≥ 0\)
    2. \(\dfrac{2x − 3}{x + 1} ≤ 0\)
    3. \(\dfrac{x + 2}{x − 2} ≥ 0\)
    الحل
    1. \(\begin{array} &&\dfrac{x − 1}{x + 1} ≥ 0 &\text{Example problem} \\ &\dfrac{x − 1}{x + 1} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).}\\ &x − 1 = 0،\؛ x = 1 &\ text {ابحث عن أصفار البسط}\\ &x + 1 = 0، x =\؛ −1 &\ text {ابحث عن أصفار المقام}\ النهاية {المصفوفة}\)
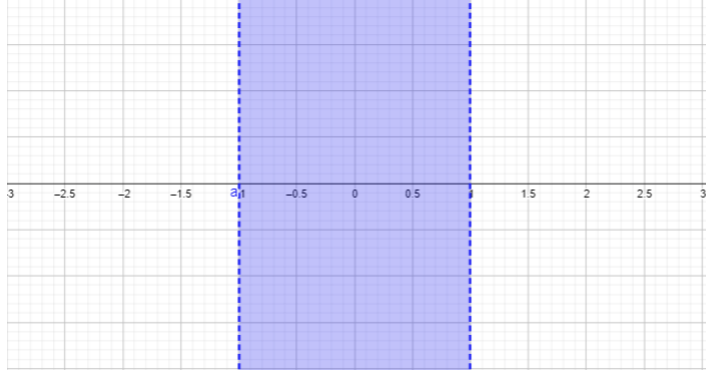
    clipboard_ec11760d50b919ddd83bc64d27535e4b7.png
    تقسم الأصفار خط الأرقام إلى\(3\) مناطق،\(x < −1\)،\(−1 < x < 1\)،\(x > 1\)

    \(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\;\dfrac{−2 − 1}{−2 + 1} = \dfrac{−3}{−1} = 3 ≥ 0 \\ &\text{Replacing \(-2\)للحصول على\(x\) نتائج في الإجابة\(3\)، والتي تكون أكبر من أو تساوي\(0\). تم تضمين\(x < −1\) هذه المنطقة في مجموعة الحلول.}\\ [0.25 بوصة] و\ text {For} −1 < x < 1،\ text {choose} x = 0.\؛\ dfrac {0 − 1} {0 + 1} =\ dfrac {−1} {1} = −1} = −1} = −1 < 0\\\ النص {استبدال\(0\)\(x\) النتائج في الإجابة\(-1\)، وهي أقل من\(0\)، غير محققة عدم المساواة المعطاة في المشكلة.}\\\\ النص {تم استبعاد هذه المنطقة\(−1 < x < 1\) من مجموعة الحلول.}\\ [0.25 بوصة] و\ text {لـ} x > 1،\ text {choose} x = 2.\;\;\ dfrac {2 − 1} {2} {2} {2} =\ dfrac {1} {3} ≥ 0\\\\ {استبدال\(2\) النص\(x\) بالنتائج في الإجابة\(\dfrac{1}{3}\)، والتي هو أكبر من أو يساوي\(0\). تم تضمين\(x > 1\) هذه المنطقة في مجموعة الحلول.}\\ [0.25 بوصة] & (−∞، −1) (1، ∞)\\ &\ text {الإجابة النهائية مكتوبة بتدوين فاصل زمني (راجع القسم الخاص بالتدوين الفاصل الزمني لمزيد من التفاصيل).} \ end {مصفوفة}\)

    1. \(\begin{array} &&\dfrac{2x − 3}{x + 1} ≤ 0 &\text{Example problem} \\ &\dfrac{2x − 3}{x + 1} ≤ 0 &\text{The quotient must be less than or equal to \(0\).}\\ &2x − 3 = 0،\؛ x = 1.5 &\ text {ابحث عن أصفار البسط}\\ &x + 1 = 0،\؛ x = −1 &\ text {ابحث عن أصفار المقام}\ النهاية {المصفوفة}\)
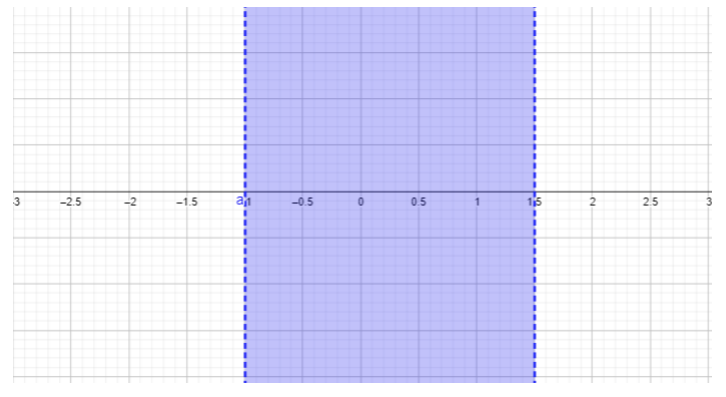
    clipboard_eb1a3fd2706ba7b03d6acdeb3ad51ec07.png
    تقسم الأصفار خط الأرقام إلى\(3\) مناطق،\(x < −1\)،\(−1 < x < 1.5\)،\(x > 1.5\)

    \(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\; \dfrac{2(−2) − 3}{−2 − 1} = \dfrac{−7}{−3} = \dfrac{7}{3} ≥ 0 \\ &\text{Replacing \(-2\)للحصول على\(x\) نتائج في الإجابة\(\dfrac{7}{3}\)، وهي أكبر من\(0\)، عدم تحقيق عدم المساواة المحددة في المشكلة.}\\ &\ text {تم استبعاد هذه المنطقة\(x < −1\) من مجموعة الحلول.}\\ [0.25in] &\ text {For} −1 < x < 1.5،\ text {choose} x = 0.\؛\\ dfrac {2 (0) - 3} {0 − 1} =\ dfrac {−3} {−1} = 3 ≥ 0\\ &\ text {استبدال\(0\)\(x\) النتائج في الإجابة\(3\)، التي تكون أكبر من أو تساوي\(0\)، وهو ليس ما تطلبه المشكلة.}\\ &\ text {تم استبعاد هذه المنطقة\(−1 < x < 1.5\) في مجموعة الحلول.}\\ [0.25 بوصة] &\ text {لـ } x > 1،\ text {choose} x = 2.\؛\؛\ dfrac {2 (2) − 3} {2 − 1} =\ dfrac {1} {1} = 1 ≥ 0\\\\ text {استبدال\(2\)\(x\) النتائج في الإجابة\(1\)، والتي تكون أكبر من أو تساوي\(0\). تم استبعاد\(x > 1\) هذه المنطقة في مجموعة الحلول.}\\ [0.25in] &\\\\ text {لا يوجد حل لهذه المشكلة. \(\dfrac{2x − 3}{x + 1}\)لن تكون أبدًا أقل من أو مساوية لـ\(0\).} \ end {مصفوفة}\)

    1. \(\begin{array} &&\dfrac{x + 2}{x − 2} ≥ 0 &\text{Example problem} \\ &\dfrac{x + 2}{x − 2} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).}\\ &x + 2 = 0,\;\;\; x = −2 &\ text {ابحث عن أصفار البسط}\\ &x − 2 = 0,\;\;\; x = 2 &\ النص {ابحث عن أصفار المقام}\ النهاية {المصفوفة}\)
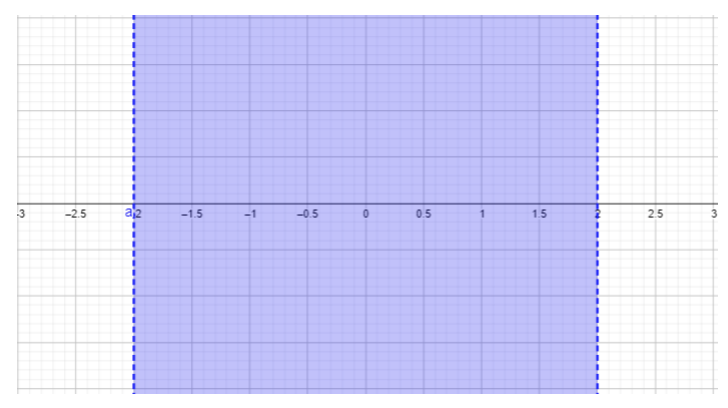
    clipboard_e3374fd2eab55feb8c3dfe2d5ebd8d557.png
    تقسم الأصفار خط الأرقام إلى\(3\) مناطق،\(x < −2\)،\(−2 < x < 2\)،\(x > 2\)

    \(\begin{array} &&\text{For } x < −2, \text{ choose } x = −3. \dfrac{−3 + 2}{−3 − 2} = \dfrac{−1}{−5} = \dfrac{1}{5} ≥ 0 \\ &\text{Replacing \(-3\)للحصول على\(x\) نتائج في الإجابة\(\dfrac{1}{5}\)، والتي تكون أكبر من أو تساوي\(0\). تم تضمين\(x < −2\) هذه المنطقة في مجموعة الحلول.}\\ [0.25 بوصة] و\ text {For} −2 < x < 2،\ text {choose} x = 0.\؛\ dfrac {0 + 2} {0 − 2} =\ dfrac {2} {2} = −1 < 0\\\\ النص {استبدال\(0\)\(x\) النتائج في الإجابة\(-1\)، وهي أقل من\(0\)، غير محققة عدم المساواة المعطاة في المشكلة.}\\\\ النص {هذه المنطقة\(−2 < x < 2\) غير مضمنة في مجموعة الحلول.}\\ [0.25 بوصة] و\ النص {لـ} x > 2،\ النص {اختر} x = 3.\؛\؛\ dfrac {3 + 2} {3 − 2} =\ dfrac {5} {1} = 5 ≥ 0\\\\\ النص {استبدال\(3\)\(x\) النتائج في الإجابة\(5\)، وهو أكبر من أو يساوي\(0\). تم تضمين\(x > 2\) هذه المنطقة في مجموعة الحلول.}\\ [0.25 بوصة] & (−∞، −2) (2، ∞)\\ &\ text {الإجابة النهائية مكتوبة بتدوين فاصل زمني (راجع القسم الخاص بالتدوين الفاصل الزمني لمزيد من التفاصيل).} \ end {مصفوفة}\)

    التمرين
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/10:_عدم_المساواة/10.03:_عدم_المساواة_العقلانية), /content/body/section[2]/header/div/h5/span/span, line 1, column 17
    1. \(\dfrac{x + 3}{x − 2} ≥ 0\)
    2. \(\dfrac{x − 2}{x − 1} ≤ 0\)
    3. \(\dfrac{2x − 1}{x + 2} ≤ 0\)
    4. \(\dfrac{2x − 3}{x + 1} ≥ 0\)