19.2: مسح النجوم

Last updated
Save as PDF

Page ID: 197272

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

فهم مفهوم تثليث المسافات إلى الأجسام البعيدة، بما في ذلك النجوم
اشرح لماذا تقدم الأقمار الصناعية الفضائية مسافات أكثر دقة من الأساليب الأرضية
ناقش جهود علماء الفلك لدراسة النجوم الأقرب إلى الشمس

إنها خطوة هائلة للانتقال من الكواكب إلى النجوم. على سبيل المثال، سافر مسبار Voyager 1، الذي تم إطلاقه في عام 1977، الآن بعيدًا عن الأرض أكثر من أي مركبة فضائية أخرى. كما هو مكتوب في عام 2016، يقع Voyager 1 على بعد 134 AU من الشمس. ¹ ومع ذلك، فإن أقرب نجم هو مئات الآلاف من AU من الأرض. ومع ذلك، يمكننا، من حيث المبدأ، مسح المسافات إلى النجوم باستخدام نفس الأسلوب الذي يستخدمه مهندس مدني لمسح المسافة إلى جبل أو شجرة يتعذر الوصول إليها - طريقة التثليث.

التثليث في الفضاء

مثال عملي على التثليث هو إدراك العمق الخاص بك. كما يسعدك أن تكتشف كل صباح عندما تنظر في المرآة، تقع عيناك على مسافة بعيدة. لذلك يمكنك مشاهدة العالم من وجهتي نظر مختلفتين، وهذا المنظور المزدوج هو الذي يسمح لك بالحصول على فكرة عامة عن مدى بُعد الأشياء.

لمعرفة ما نعنيه، خذ قلمًا وأمسكه بضع بوصات أمام وجهك. انظر إليها أولاً بإحدى العينين (أغلق الأخرى) ثم بدّل العينين. لاحظ كيف يبدو القلم وكأنه يتغير بالنسبة للأشياء في جميع أنحاء الغرفة. الآن أمسك القلم بطول الذراع: التغيير أقل. إذا لعبت بتحريك القلم لفترة من الوقت، ستلاحظ أنه كلما ابتعدت عن القلم، كلما قل احتمال نقله. يقوم عقلك تلقائيًا بإجراء مثل هذه المقارنات ويمنحك إحساسًا جيدًا بمدى بُعد الأشياء في منطقتك المباشرة.

إذا كانت ذراعيك مصنوعتان من المطاط، فيمكنك مد القلم بعيدًا بما يكفي عن عينيك بحيث يصبح التحول غير محسوس. هذا لأن إدراكنا للعمق يفشل في الأشياء التي تبعد أكثر من بضع عشرات من الأمتار. من أجل رؤية تحول كائن يقع على بعد كتلة مدينة أو أكثر منك، يجب أن تكون عيناك متباعدتين كثيرًا.

دعونا نرى كيف يستفيد المساحون من نفس الفكرة. لنفترض أنك تحاول قياس المسافة إلى شجرة عبر نهر عميق (الشكل\(\PageIndex{1}\)). قمت بإعداد محطتي مراقبة على بعد مسافة. هذه المسافة (الخط AB في الشكل\(\PageIndex{1}\)) تسمى خط الأساس. الآن يتم ملاحظة اتجاه الشجرة (C في الشكل) فيما يتعلق بخط الأساس من كل محطة. لاحظ أن C تظهر في اتجاهات مختلفة من المحطتين. هذا التغيير الواضح في اتجاه الكائن البعيد بسبب التغيير في وجهة نظر الراصد يسمى اختلاف المنظر.

بديل — الشكل:\(\PageIndex{1}\) التثليث. يتيح لنا التثليث قياس المسافات إلى الأشياء التي يتعذر الوصول إليها. من خلال الحصول على زاوية الشجرة من نقطتين مختلفتين، يمكننا حساب خصائص المثلث الذي تصنعه وبالتالي المسافة إلى الشجرة.

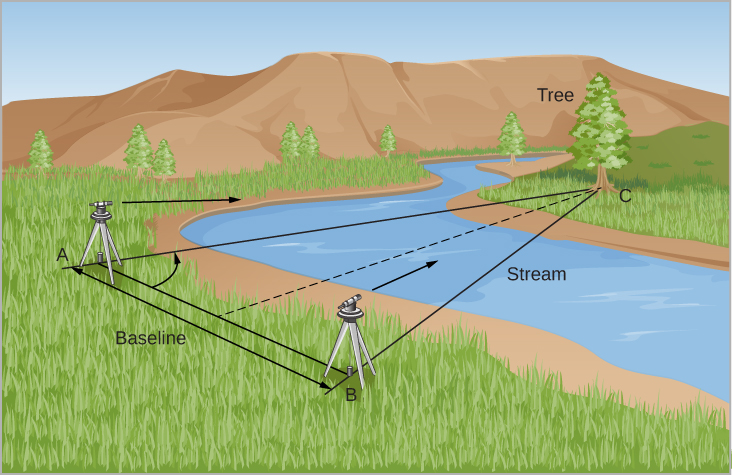
المنظر هو أيضًا الزاوية التي يصنعها الخطان AC و BC - من الناحية الرياضية، الزاوية المقابلة للخط الأساسي. تسمح معرفة الزوايا عند A و B وطول خط الأساس، AB، بحل المثلث ABC لأي من أبعاده - على سبيل المثال، المسافة AC أو BC. يمكن الوصول إلى الحل من خلال إنشاء رسم تخطيطي أو باستخدام علم المثلثات لإجراء حساب عددي. إذا كانت الشجرة بعيدة، فسيكون المثلث بأكمله أطول وأكثر نحافة، وستكون زاوية المنظر أصغر. وبالتالي، لدينا قاعدة عامة مفادها أنه كلما كان المنظر أصغر، يجب أن يكون الكائن الذي نقيسه أكثر بعدًا.

من الناحية العملية، تكون أنواع خطوط الأساس التي يستخدمها المساحون لقياس المسافات على الأرض عديمة الفائدة تمامًا عندما نحاول قياس المسافات في الفضاء. كلما كان الكائن الفلكي بعيدًا، كلما كان خط الأساس أطول لإعطائنا فرصة معقولة لإجراء القياس. لسوء الحظ، فإن جميع الكائنات الفلكية تقريبًا بعيدة جدًا. يتطلب قياس مسافاتها خطًا أساسيًا كبيرًا جدًا وقياسات زاوية دقيقة للغاية. القمر هو الكائن الوحيد القريب بما يكفي بحيث يمكن العثور على مسافته بدقة إلى حد ما من خلال القياسات التي تتم بدون تلسكوب. حدد بطليموس المسافة إلى القمر بشكل صحيح في حدود نسبة قليلة. استخدم دوران الأرض نفسه كأساس لقياس موقع القمر بالنسبة للنجوم في وقتين مختلفين من الليل.

بمساعدة التلسكوبات، تمكن علماء الفلك لاحقًا من قياس المسافات إلى الكواكب والكويكبات الأقرب باستخدام قطر الأرض كخط أساس. هذه هي الطريقة التي تم بها تأسيس الاتحاد الأفريقي لأول مرة. ومع ذلك، فإن الوصول إلى النجوم يتطلب خطًا أساسيًا أطول بكثير لعمليات التثليث والقياسات الحساسة للغاية. يتم توفير هذا الخط الأساسي من خلال رحلة الأرض السنوية حول الشمس.

المسافات إلى النجوم

عندما تنتقل الأرض من أحد جانبي مدارها إلى الآخر، فإنها تزودنا بلطف بخط أساس يبلغ 2 AU، أو حوالي 300 مليون كيلومتر. على الرغم من أن هذا خط الأساس أكبر بكثير من قطر الأرض، إلا أن النجوم بعيدة جدًا لدرجة أن تحول المنظر الناتج لا يزال غير مرئي للعين المجردة - ولا حتى لأقرب النجوم.

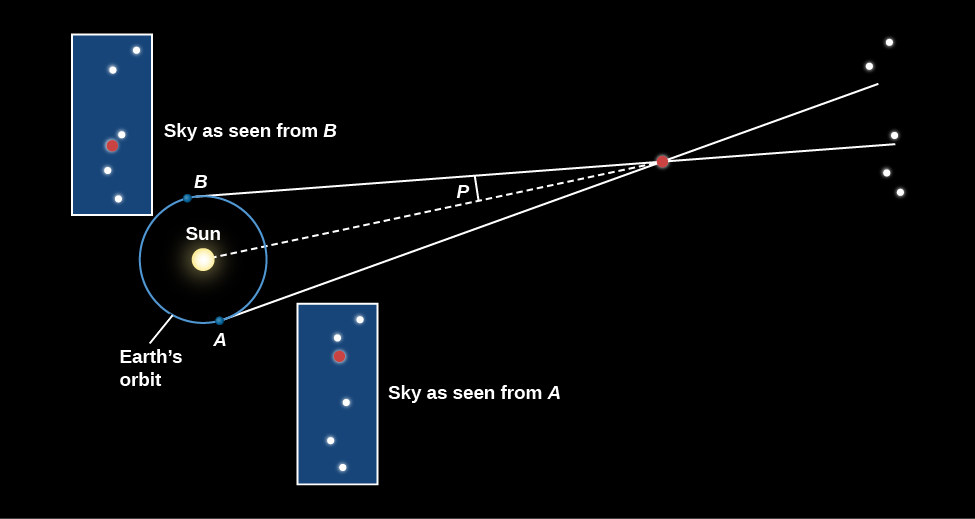
في الفصل الخاص بمراقبة السماء: ولادة علم الفلك، ناقشنا كيف أدت هذه المعضلة إلى حيرة الإغريق القدماء، الذين اقترح بعضهم بالفعل أن الشمس قد تكون مركز النظام الشمسي، مع تحرك الأرض حولها. لكن أرسطو وآخرون جادلوا بأن الأرض لا يمكن أن تدور حول الشمس. وقالوا إنه إذا كان الأمر كذلك، فسنلاحظ بالتأكيد اختلاف النجوم القريبة على خلفية الأجسام البعيدة بينما كنا نشاهد السماء من أجزاء مختلفة من مدار الأرض (الشكل\(\PageIndex{3}\)). قدم تايكو براهي (1546-1601) نفس الحجة الخاطئة بعد ما يقرب من 2000 عام، عندما لم تكشف قياساته الدقيقة للمواضع النجمية بالعين المجردة عن مثل هذا التحول.

لم يدرك هؤلاء المراقبون الأوائل مدى بُعد النجوم حقًا ومدى صغر التغيير في مواقعها، حتى مع وجود مدار الأرض بأكمله كخط أساس. كانت المشكلة أنهم لم يكن لديهم أدوات لقياس تحولات المنظر الصغيرة جدًا بحيث لا يمكن رؤيتها بالعين البشرية. بحلول القرن الثامن عشر، عندما لم يعد هناك شك جدي حول ثورة الأرض، أصبح من الواضح أن النجوم يجب أن تكون بعيدة للغاية. بدأ علماء الفلك المجهزون بالتلسكوبات في ابتكار أدوات قادرة على قياس التحولات الصغيرة للنجوم القريبة بالنسبة لخلفية الأجسام السماوية الأكثر بعدًا (وبالتالي عدم الحركة).

كان هذا تحديًا تقنيًا كبيرًا، لأنه حتى بالنسبة لأقرب النجوم، عادة ما تكون زوايا المنظر جزءًا من الثانية فقط من القوس. تذكر أن ثانية واحدة من القوس (arcsec) هي زاوية 1/3600 فقط من الدرجة. يبدو أن عملة بحجم ربع دولار أمريكي يبلغ قطرها 1 قوس ثانية إذا كنت تشاهدها من مسافة حوالي 5 كيلومترات (3 أميال). فكر في مدى صغر هذه الزاوية. لا عجب أن الأمر استغرق علماء الفلك وقتًا طويلاً قبل أن يتمكنوا من قياس مثل هذه التحولات الصغيرة.

كانت أولى الاكتشافات الناجحة لاختلاف المنظر النجمي في عام 1838، عندما قام فريدريش بيسيل في ألمانيا (الشكل\(\PageIndex{2}\))، وتوماس هندرسون، عالم الفلك الاسكتلندي الذي يعمل في رأس الرجاء الصالح، وفريدريك ستروف في روسيا بشكل مستقل بقياس مناظر النجوم 61 Cygni و Alpha Centauri، وفيغا، على التوالي. حتى النجم الأقرب، Alpha Centauri، أظهر نزوحًا إجماليًا يبلغ حوالي 1.5 ثانية فقط خلال العام.

\(\PageIndex{3}\)يوضح الشكل كيفية عمل هذه القياسات. عند رؤيته من جوانب متقابلة من مدار الأرض، يغير النجم القريب موضعه عند مقارنته بنمط النجوم الأكثر بعدًا. يعرّف علماء الفلك في الواقع اختلاف المنظر على أنه نصف الزاوية التي يحركها النجم عند رؤيته من جوانب متقابلة من مدار الأرض (الزاوية المسماة P في الشكل\(\PageIndex{3}\)). سبب هذا التعريف هو أنهم يفضلون التعامل مع خط الأساس لـ 1 AU بدلاً من 2 AU.

وحدات المسافة النجمية

باستخدام خط الأساس الخاص بوحدة AU واحدة، إلى أي مدى يجب أن يكون النجم بعيدًا حتى يكون له اختلاف قدره 1 قوس ثانية؟ تبين أن الإجابة هي 206,265 AU، أو 3.26 سنة ضوئية. هذا يساوي 3.1 × 10 ¹³ كيلومترًا (بمعنى آخر، 31 تريليون كيلومتر). نطلق على هذه الوحدة اسمًا خاصًا، وهو parsec (pc) - مشتق من «المسافة التي لدينا فيها تساوي ثانية واحدة». المسافة (\(D\)) للنجم في الفرس هي مجرد مقلوب اختلاف المنظر (p) بالثواني القوسمية؛ أي،

\[D=\frac{1}{p} \nonumber\]

وهكذا، يمكن العثور على نجمة ذات اختلاف المنظر بمقدار 0.1 قوس ثانية على مسافة 10 أجزاء، والنجمة التي لها اختلاف المنظر بمقدار 0.05 قوس من الثانية ستكون على بعد 20 فرسخ.

في الأيام التي كانت فيها معظم مسافاتنا تأتي من قياسات المنظر، كان الفرسك وحدة مفيدة للمسافة، ولكنه ليس بديهيًا مثل السنة الضوئية. تتمثل إحدى مزايا السنة الضوئية كوحدة في أنها تؤكد على حقيقة أننا، عندما ننظر إلى الفضاء، ننظر أيضًا إلى الزمن إلى الوراء. الضوء الذي نراه من نجم على بعد 100 سنة ضوئية ترك هذا النجم قبل 100 عام. ما ندرسه ليس النجم كما هو الآن، بل كما كان في الماضي. الضوء الذي يصل إلى التلسكوبات الخاصة بنا اليوم من المجرات البعيدة تركها قبل وجود الأرض.

في هذا النص، سنستخدم السنوات الضوئية كوحدة للمسافة، لكن العديد من علماء الفلك لا يزالون يستخدمون الفرسيكات عند كتابة الأوراق الفنية أو التحدث مع بعضهم البعض في الاجتماعات. للتحويل بين وحدتي المسافة، ضع في اعتبارك: 1 بارسيك = 3.26 سنة ضوئية، و 1 سنة ضوئية = 0.31 بارسيك.

مثال\(\PageIndex{1}\): كم تبعد السنة الضوئية؟

السنة الضوئية هي المسافة التي يقطعها الضوء في عام واحد. إذا كان الضوء ينتقل بسرعة 300,000 كم/ثانية، فما عدد الكيلومترات الموجودة في السنة الضوئية؟

الحل

لقد تعلمنا سابقًا أن السرعة = المسافة/الوقت. يمكننا إعادة ترتيب هذه المعادلة بحيث\(\text{distance } = \text{ velocity } \times \text{ time }\). الآن، نحتاج إلى تحديد عدد الثواني في السنة.

هناك ما يقرب من 365 يومًا في عام واحد. لتحديد عدد الثواني، يجب علينا تقدير عدد الثواني في يوم واحد.

يمكننا تغيير الوحدات على النحو التالي (لاحظ كيفية إلغاء الوحدات الزمنية):

\[ 1 \text{ day } \times 24 \text{ hr/day } \times 60 \text{ min/hr } \times 60 \text{ s/min } = 86,400 \text{ s/day} \nonumber\]

بعد ذلك، للحصول على عدد الثواني في السنة:

\[ 365 \text{ days/year } \times 86,400 \text{ s/day } = 31,536,000 \text{ s/year} \nonumber\]

يمكننا الآن ضرب سرعة الضوء بعدد الثواني في السنة للحصول على المسافة التي يقطعها الضوء في عام واحد:

\[ \begin{aligned} \text{distance } & = \text{ velocity } \times \text{ time} \\ & = 300,000 \text{ km/s } \times 31,536,000 \text{ s} \\ & =9.46 \times 10^{12} \text{ km} \end{aligned} \nonumber\]

هذا ما يقرب من 10,000 مليون كيلومتر يغطيه الضوء في السنة. لمساعدتك على تخيل طول هذه المسافة، سنذكر أن سلسلة طولها سنة ضوئية واحدة يمكن أن تناسب محيط الأرض 236 مليون مرة.

التمارين\(\PageIndex{1}\)

الرقم أعلاه كبير حقًا. ماذا يحدث إذا وضعناها بعبارات قد تكون أكثر قابلية للفهم، مثل قطر الأرض؟ يبلغ قطر الأرض حوالي 12700 كم.

إجابة

\[ \begin{aligned} 1 \text{ light-year } & = 9.46 \times 10^{12} \text{ km} \\ & =9.46 \times 10^{12} \text{ km } \times \frac{1 \text{ Earth diameter}}{12,700 \text{ km}} \\ & =7.45 \times 10^8 \text{ Earth diameters} \end{aligned} \nonumber\]

وهذا يعني أن السنة الضوئية الواحدة تبلغ حوالي 745 مليون مرة من قطر الأرض.

تسمية النجوم

قد تتساءل لماذا تمتلك النجوم مثل هذه المجموعة المربكة من الأسماء. ما عليك سوى إلقاء نظرة على النجوم الثلاثة الأولى التي تم قياس اختلافاتها: 61 Cygni و Alpha Centauri و Vega. يأتي كل اسم من هذه الأسماء من تقليد مختلف لتسمية النجوم.

النجوم الأكثر سطوعًا لها أسماء مشتقة من القدماء. بعضها من اليونانية، مثل سيريوس، والتي تعني «المحروقة» - إشارة إلى تألقها. بعضها من اللاتينية، ولكن العديد من الأسماء الأكثر شهرة هي من اللغة العربية لأنه، كما تمت مناقشته في «رصد السماء: ولادة علم الفلك»، تم «إعادة اكتشاف» الكثير من علم الفلك اليوناني والروماني في أوروبا بعد العصور المظلمة عن طريق الترجمات العربية. فيجا، على سبيل المثال، تعني «النسر المنقضاض»، بينما تعني كلمة بيتلجيوز (التي تُلفظ «عصير الخنفساء») «اليد اليمنى للوسط».

في عام 1603، قدم عالم الفلك الألماني يوهان باير (1572-1625) نهجًا أكثر انتظامًا لتسمية النجوم. بالنسبة لكل كوكبة، خصص حرفًا يونانيًا للنجوم الأكثر سطوعًا، بترتيب السطوع تقريبًا. في كوكبة أوريون، على سبيل المثال، يعتبر Betelgeuse هو النجم الأكثر سطوعًا، لذلك حصل على الحرف الأول في الأبجدية اليونانية - ألفا - ويعرف باسم Alpha Orionis. («Orionis» هو شكل الملكية لـ Orion، لذا فإن Alpha Orionis تعني «أول أوريون».) يُطلق على النجم المسمى Rigel، وهو ثاني ألمع نجم في تلك الكوكبة، اسم Beta Orionis (الشكل\(\PageIndex{4}\)). نظرًا لوجود 24 حرفًا في الأبجدية اليونانية، يسمح هذا النظام بوضع علامات على 24 نجمة في كل كوكبة، لكن الأبراج تحتوي على نجوم أكثر من ذلك بكثير.

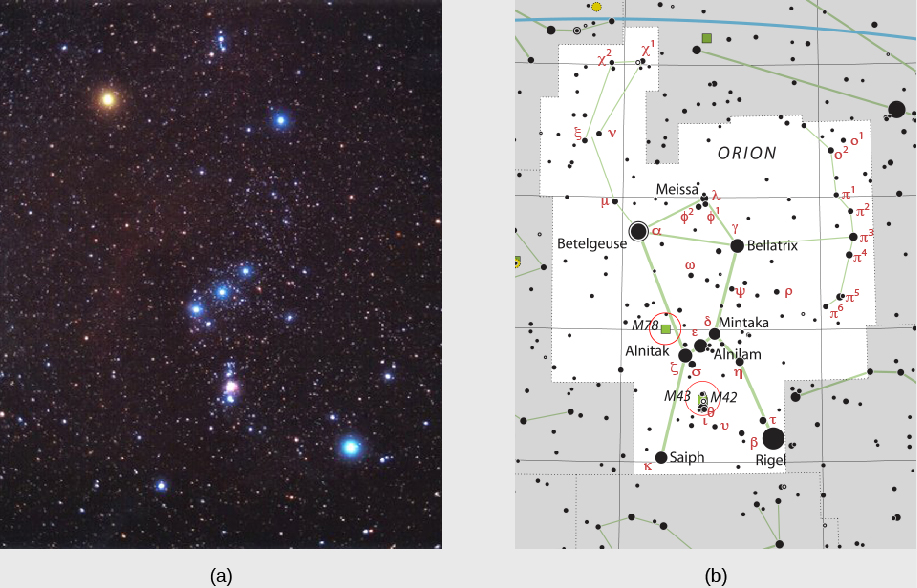
في عام 1725، قدم عالم الفلك الإنجليزي رويال جون فلامستيد نظامًا آخر، حيث حصلت النجوم الأكثر إشراقًا في النهاية على رقم في كل كوكبة بترتيب موقعها في السماء أو، بشكل أدق، صعودها الصحيح. (تمت مناقشة نظام إحداثيات السماء الذي يتضمن الصعود الأيمن في الأرض والقمر والسماء.) في هذا النظام، يُطلق على Betelgeuse اسم 58 Orionis و 61 Cygni هو النجم 61 في كوكبة Cygnus، البجعة.

الأمر يزداد سوءًا. عندما بدأ علماء الفلك في فهم المزيد والمزيد عن النجوم، وضعوا سلسلة من كتالوجات النجوم المتخصصة، وبدأ عشاق تلك الكتالوجات في الاتصال بالنجوم من خلال أرقام الكتالوج الخاصة بهم. إذا نظرت إلى الملحق الأول - قائمتنا لأقرب النجوم (العديد منها خافت جدًا بحيث لا يمكن الحصول على اسم قديم أو حرف Bayer أو رقم Flamsteed) - سترى مراجع لبعض هذه الكتالوجات. ومن الأمثلة على ذلك مجموعة من النجوم تحمل رقم BD، لـ «Bonner Durchmusterung». كان هذا كتالوجًا ضخمًا يضم أكثر من 324 ألف نجم في سلسلة من المناطق في السماء، وقد تم تنظيمه في مرصد بون في خمسينيات وستينيات القرن التاسع عشر. ضع في اعتبارك أن هذا الكتالوج تم إعداده قبل استخدام التصوير الفوتوغرافي أو أجهزة الكمبيوتر، لذلك كان يجب قياس موضع كل نجمة (مرتين على الأقل) بالعين، وهي مهمة شاقة.

هناك أيضًا نظام مختلف تمامًا لتتبع النجوم التي يختلف لمعانها، ونظام آخر للنجوم التي تضيء بشكل متفجر في أوقات غير متوقعة. لقد اعتاد علماء الفلك على العديد من أنظمة تسمية النجوم المختلفة، لكن الطلاب غالبًا ما يجدونها محيرة ويتمنون أن يستقر علماء الفلك على واحدة. لا تحبس أنفاسك: في علم الفلك، كما هو الحال في العديد من مجالات الفكر الإنساني، تتمتع التقاليد بجاذبية قوية. ومع ذلك، مع قواعد بيانات الكمبيوتر عالية السرعة لمساعدة الذاكرة البشرية، قد تصبح الأسماء أقل أهمية. غالبًا ما يشير علماء الفلك اليوم إلى النجوم من خلال مواقعها الدقيقة في السماء بدلاً من أسمائها أو أرقام الكتالوج المختلفة.

أقرب النجوم

لا يوجد نجم معروف (بخلاف الشمس) في غضون سنة ضوئية واحدة أو حتى جزء واحد من الأرض. الجيران النجميون الأقرب إلى الشمس هم ثلاثة نجوم في كوكبة Centaurus. بالنسبة للعين المجردة، فإن ألمع هذه النجوم الثلاثة هو Alpha Centauri، الذي يبعد 30 درجة فقط عن القطب السماوي الجنوبي وبالتالي لا يمكن رؤيته من البر الرئيسي للولايات المتحدة. يعد Alpha Centauri نفسه نجمًا ثنائيًا - نجمان في ثورة متبادلة - قريبان جدًا من بعضهما البعض بحيث لا يمكن تمييزهما بدون تلسكوب. يقع هذان النجمان على بعد 4.4 سنة ضوئية منا. في الجوار توجد نجمة خافتة ثالثة تُعرف باسم Proxima Centauri. بروكسيما، بمسافة 4.3 سنة ضوئية، أقرب إلينا قليلاً من النجمين الآخرين. إذا كانت Proxima Centauri جزءًا من نظام النجوم الثلاثية مع نظام Alpha Centauri الثنائي، كما يبدو مرجحًا، فقد تكون فترته المدارية أطول من 500,000 عام.

Proxima Centauri هو مثال على أكثر أنواع النجوم شيوعًا، والنوع الأكثر شيوعًا لدينا من الجيران النجميين (كما رأينا في Stars: A Celestial Census.) تشكل أقزام M الحمراء منخفضة الكتلة حوالي 70٪ من جميع النجوم وتهيمن على تعداد النجوم في حدود 10 أجزاء من الشمس. أحصت أحدث دراسة استقصائية للحي الشمسي 357 نجمًا وأقزامًا بنية في غضون 10 فرسخ، و248 منها من الأقزام الحمراء. ومع ذلك، إذا كنت ترغب في رؤية قزم M بعينك المجردة، فلن يحالفك الحظ. تنتج هذه النجوم جزءًا صغيرًا فقط من ضوء الشمس، وتتطلب جميعها تقريبًا تلسكوبًا ليتم اكتشافه.

أقرب نجم مرئي بدون تلسكوب من معظم الولايات المتحدة هو النجم الأكثر سطوعًا بين جميع النجوم، سيريوس، الذي تبلغ مسافته أكثر بقليل من 8 سنوات ضوئية. إنه أيضًا نظام ثنائي، يتكون من قزم أبيض خافت يدور حول نجم تسلسلي رئيسي أبيض مزرق. من قبيل المصادفة المثيرة للأرقام أن الضوء يصل إلينا من الشمس في حوالي 8 دقائق ومن النجم التالي الأكثر سطوعًا في السماء في حوالي 8 سنوات.

مثال\(\PageIndex{2}\): حساب قطر الشمس

بالنسبة للنجوم القريبة، يمكننا قياس التحول الواضح في مواقعها عندما تدور الأرض حول الشمس. لقد كتبنا سابقًا أن الكائن يجب أن يكون على بعد 206,265 AU حتى يكون له اختلاف في ثانية واحدة من القوس. يجب أن يبدو هذا رقمًا غريبًا جدًا، ولكن يمكنك معرفة سبب كون هذه هي القيمة الصحيحة. سنبدأ بتقدير قطر الشمس ثم نطبق نفس الفكرة على نجمة ذات اختلاف قدره 1 قوس ثانية. ارسم رسمًا يحتوي على دائرة مستديرة لتمثيل الشمس، ثم ضع الأرض على بُعد مسافة، ثم ضع راصدًا عليها. ارسم سطرين من النقطة التي يقف فيها الراصد، أحدهما على كل جانب من جوانب الشمس. ارسم دائرة متمركزة على الأرض ومحيطها يمر عبر مركز الشمس. الآن فكر في النسب. تمتد الشمس حوالي نصف درجة في السماء. تحتوي الدائرة الكاملة على 360○. يتم تحديد محيط الدائرة التي تتمركز على الأرض والتي تمر عبر الشمس من خلال:

\[\text{circumference } =2 \pi \times 93,000,000 \text{ miles} \nonumber\]

ثم تتساوى النسبتان التاليتان:

\[\frac{0.5^{\circ}}{360^{\circ}} = \frac{\text{diameter of Sun}}{2 \pi \times 93,000,000} \nonumber\]

احسب قطر الشمس. كيف تقارن إجابتك بالقطر الفعلي؟

الحل

لحل قطر الشمس، يمكننا تقييم التعبير أعلاه.

\ [\ ابدأ {محاذاة}\ النص {قطر الشمس} و =\ frac {0.5^ {\\ circ} {360 ^ {\ circ}}
\ مرات 2\ pi\ مرات 93,000,000\ نص {أميال}\ =811,577\ نص {أميال}\\ نهاية {محاذاة}\ لا رقم\]

هذا قريب جدًا من القيمة الحقيقية لحوالي 848,000 ميل.

التمارين\(\PageIndex{2}\)

الآن قم بتطبيق هذه الفكرة لحساب المسافة إلى نجمة لها اختلاف قدره 1 arcsec. ارسم صورة مشابهة لتلك التي اقترحناها أعلاه واحسب المسافة في AU. (تلميح: تذكر أن زاوية اختلاف المنظر محددة بـ 1 AU، وليس 2 AU، وأن 3600 قوس ثانية = 1 درجة.)

إجابة: 206,265 دولار أسترالي

قياس أوجه التباين في الفضاء

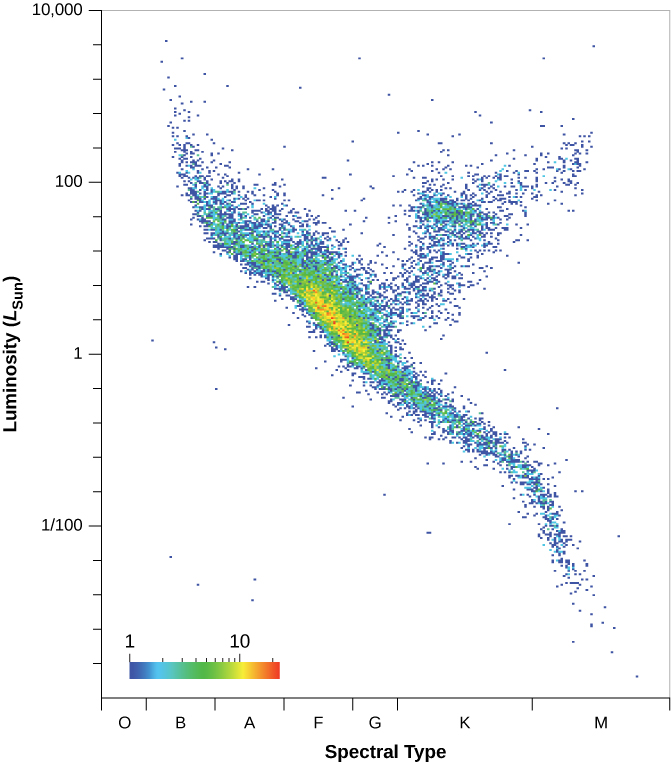
أحدثت قياسات المنظر النجمي ثورة من خلال إطلاق المركبة الفضائية Hipparcos في عام 1989، والتي قاست مسافات آلاف النجوم حتى حوالي 300 سنة ضوئية بدقة تتراوح من 10 إلى 20٪ (انظر الشكل\(\PageIndex{5}\) والميزة في Parallax وعلم الفلك الفضائي أدناه). ومع ذلك، حتى 300 سنة ضوئية تقل عن 1٪ من حجم القرص الرئيسي لجهاز Galaxy.

في ديسمبر 2013، تم إطلاق خليفة هيباركوس، المسمى Gaia، من قبل وكالة الفضاء الأوروبية. تقوم Gaia بقياس الموقع والمسافات إلى ما يقرب من مليار نجم بدقة تبلغ بضعة ملايين من الثانية القوسية. سيمتد الحد الأقصى لمسافة Gaia إلى ما وراء Hipparcos، حيث سيدرس النجوم حتى 30000 سنة ضوئية (أبعد 100 مرة من هيباركوس، ويغطي ما يقرب من 1/3 من قرص المجرة). ستكون Gaia أيضًا قادرة على قياس الحركات المناسبة ² لآلاف النجوم في هالة درب التبانة - وهو أمر لا يمكن القيام به إلا لألمع النجوم في الوقت الحالي. في نهاية مهمة Gaia، لن يكون لدينا فقط خريطة ثلاثية الأبعاد لجزء كبير من مجرة درب التبانة الخاصة بنا، ولكن سيكون لدينا أيضًا رابط قوي في سلسلة المسافات الكونية التي نناقشها في هذا الفصل. ومع ذلك، لتوسيع هذه السلسلة بعيدًا عن متناول Gaia واستكشاف المسافات إلى المجرات القريبة، نحتاج إلى بعض التقنيات الجديدة تمامًا.

اختلاف المنظر وعلم الفلك الفضائي

من أصعب الأمور في القياس الدقيق للزوايا الدقيقة لتحولات المنظر من الأرض أنه يجب عليك مراقبة النجوم من خلال الغلاف الجوي لكوكبنا. كما رأينا في مجلة الآلات الفلكية، فإن تأثير الغلاف الجوي هو نشر نقاط ضوء النجوم إلى أقراص غامضة، مما يجعل القياسات الدقيقة لمواقعها أكثر صعوبة. لطالما حلم علماء الفلك بالقدرة على قياس التباينات من الفضاء، وقد حوّل مرصدان مداريان هذا الحلم إلى حقيقة.

إن اسم القمر الصناعي Hipparcos، الذي أطلقته وكالة الفضاء الأوروبية في عام 1989، هو اختصار لساتل Parallax Collecting Satellax عالي الدقة وتكريمًا لهيبارخوس، عالم الفلك اليوناني الرائد الذي ناقشنا عمله في «مراقبة السماء: ولادة علم الفلك». تم تصميم القمر الصناعي لإجراء قياسات المنظر الأكثر دقة في التاريخ، من 36000 كيلومتر فوق الأرض. ومع ذلك، فشل محرك الصواريخ الموجود على متن الطائرة في إطلاق النار، مما يعني أنه لم يحصل على الدفعة اللازمة للوصول إلى الارتفاع المطلوب. انتهى الأمر بقضاء هيباركوس عمرها 4 سنوات في مدار بيضاوي يتراوح ارتفاعه من 500 إلى 36000 كيلومتر. في هذا المدار، سقط القمر الصناعي في أحزمة الإشعاع الأرضية كل 5 ساعات أو نحو ذلك، مما أثر أخيرًا على الألواح الشمسية التي توفر الطاقة لتشغيل الأدوات.

ومع ذلك، كانت المهمة ناجحة، مما أدى إلى كتالوجين. يعطي أحد المواضع التي تساوي 120,000 نجمة بدقة تصل إلى جزء من ألف من الثانية القوسية، أي حوالي قطر كرة الغولف في نيويورك كما تُرى من أوروبا. يحتوي الكتالوج الثاني على معلومات لأكثر من مليون نجم، تم قياس مواقعها بثلاثين ألف من الثانية القوسية. لدينا الآن قياسات تشابه دقيقة للنجوم حتى مسافات تبلغ حوالي 300 سنة ضوئية. (باستخدام التلسكوبات الأرضية، كانت القياسات الدقيقة ممكنة حتى حوالي 60 سنة ضوئية فقط.)

من أجل البناء على نجاح Hipparcos، في عام 2013، أطلقت وكالة الفضاء الأوروبية قمرًا صناعيًا جديدًا يسمى Gaia. من المقرر أن تستمر مهمة Gaia لمدة 5 سنوات. نظرًا لأن Gaia يحمل تلسكوبات أكبر من Hipparcos، فإنه يمكنه مراقبة النجوم الخافتة وقياس مواقعها بدقة أكبر 200 مرة. الهدف الرئيسي من مهمة Gaia هو عمل خريطة دقيقة ثلاثية الأبعاد لهذا الجزء من المجرة في غضون حوالي 30000 سنة ضوئية من خلال مراقبة مليار نجم 70 مرة لكل منها، وقياس مواقعها وبالتالي التباينات وكذلك سطوعها.

لفترة طويلة، كان قياس التباينات والمواقع النجمية الدقيقة بمثابة مصدر رزق للبحث الفلكي - ويرجع ذلك أساسًا إلى أن دقة القياسات لم تتحسن كثيرًا لمدة 100 عام تقريبًا. ومع ذلك، فإن القدرة على إجراء القياسات من الفضاء أحدثت ثورة في هذا المجال من علم الفلك وستستمر في توفير رابط حاسم في سلسلة المسافات الكونية لدينا.

تحتفظ وكالة الفضاء الأوروبية (ESA) بموقع إلكتروني لمهمة Gaia حيث يمكنك معرفة المزيد عن مهمة Gaia والحصول على آخر الأخبار حول ملاحظات Gaia.

لمعرفة المزيد عن هيباركوس، استكشف صفحة وكالة الفضاء الأوروبية هذه مع بودكاست وكالة الفضاء الأوروبية Charting the Galaxy - من Hipparcos إلى Gaia.

ملخص

بالنسبة للنجوم القريبة نسبيًا، يمكننا «تحديد» المسافات من خط الأساس الناتج عن الحركة السنوية للأرض حول الشمس. يُطلق على نصف التحول في موضع نجم قريب بالنسبة لنجوم خلفية بعيدة جدًا، كما يُرى من الجوانب المقابلة لمدار الأرض، اسم اختلاف المنظر لذلك النجم وهو مقياس لمسافته. الوحدات المستخدمة لقياس المسافة النجمية هي السنة الضوئية، والمسافة التي يقطعها الضوء في عام واحد، والبارسيك (pc)، ومسافة النجم مع اختلاف المنظر بمقدار 1 قوس ثانية (1 parsec = 3.26 سنة ضوئية). يقع أقرب نجم، وهو قزم أحمر، على بعد أكثر من 1 بارسيك. تم الإبلاغ عن القياسات الناجحة الأولى للاختلافات النجمية في عام 1838. تعتبر قياسات المنظر رابطًا أساسيًا في سلسلة المسافات الكونية. سمح لنا القمر الصناعي Hipparcos بقياس التباينات الدقيقة للنجوم حتى حوالي 300 سنة ضوئية، وستؤدي مهمة Gaia إلى حدوث اختلافات تصل إلى 30000 سنة ضوئية.

الحواشي

¹ للحصول على أساس للمقارنة، يدور الكوكب القزم بلوتو على مسافة متوسطة تبلغ 40 AU من الشمس، ويقع الكوكب القزم Eris حاليًا على بعد 96 AU تقريبًا من الشمس.

² الحركة الصحيحة (كما تمت مناقشتها في تحليل ضوء النجوم، هي حركة نجم عبر السماء (عموديًا على خط رؤيتنا.)

مسرد المصطلحات

إختلاف المنظر: نزوح واضح لنجم قريب ينتج عن حركة الأرض حول الشمس

بارسيك: وحدة مسافة في علم الفلك، تساوي 3.26 سنة ضوئية؛ على مسافة 1 فرسخ، يكون للنجم اختلاف قدره 1 قوس ثانية