Skip to main content
Global

19.2: גידול אוכלוסייה ורגולציה

  1. Last updated
  2. Save as PDF
  • Page ID
    208591

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    אקולוגים של אוכלוסיות עושים שימוש במגוון שיטות למודל דינמיקת האוכלוסייה. מודל מדויק אמור להיות מסוגל לתאר את השינויים המתרחשים באוכלוסייה ולחזות שינויים עתידיים.

    גידול אוכלוסייה

    שני המודלים הפשוטים ביותר של גידול האוכלוסייה משתמשים במשוואות דטרמיניסטיות (משוואות שאינן מתייחסות לאירועים אקראיים) כדי לתאר את קצב השינוי בגודל האוכלוסייה לאורך זמן. הראשון מבין המודלים הללו, צמיחה אקספוננציאלית, מתאר אוכלוסיות תיאורטיות הגדלות במספרים ללא כל הגבלה לצמיחתן. המודל השני, צמיחה לוגיסטית, מציג גבולות לצמיחת הרבייה ההולכים ומתעצמים ככל שגודל האוכלוסייה גדל. אף מודל לא מתאר כראוי אוכלוסיות טבעיות, אך הם מספקים נקודות השוואה.

    צמיחה מעריכית

    צ'ארלס דרווין, בפיתוח תיאוריית הברירה הטבעית שלו, הושפע מהכמורה האנגלי תומאס מלתוס. מלתוס פרסם את ספרו בשנת 1798 וקבע כי אוכלוסיות עם משאבי טבע בשפע גדלות במהירות רבה; עם זאת, הם מגבילים צמיחה נוספת על ידי דלדול המשאבים שלהם. הדפוס המוקדם של האצת גודל האוכלוסייה נקרא גידול מעריכי.

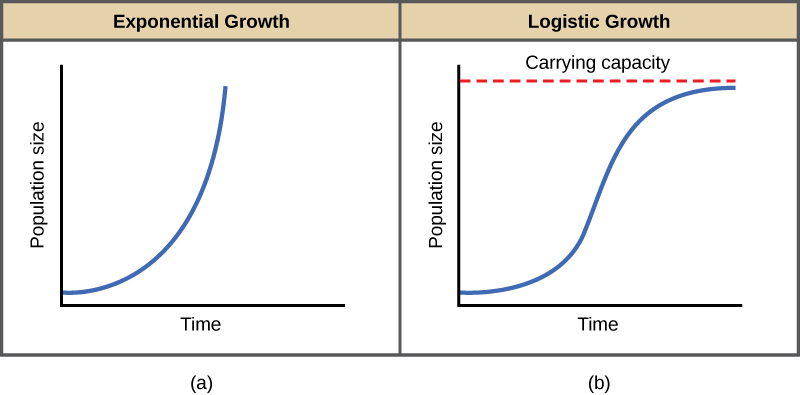
    הדוגמה הטובה ביותר לצמיחה מעריכית באורגניזמים נראית בחיידקים. חיידקים הם פרוקריוטים המתרבים בעיקר על ידי ביקוע בינארי. חלוקה זו אורכת כשעה עבור מיני חיידקים רבים. אם מניחים 1000 חיידקים בבקבוק גדול עם אספקה בשפע של חומרים מזינים (כך שהחומרים המזינים לא יתדלדלו במהירות), מספר החיידקים יוכפל מ -1000 ל -2000 לאחר שעה בלבד. בעוד שעה, כל אחד מ -2000 החיידקים יתחלק וייצר 4000 חיידקים. לאחר השעה השלישית, צריך להיות 8000 חיידקים בבקבוק. התפיסה החשובה של צמיחה מעריכית היא שקצב הגידול - מספר האורגניזמים שנוספו בכל דור רבייה - גדל בעצמו; כלומר, גודל האוכלוסייה גדל בקצב גדול יותר ויותר. לאחר 24 מהמחזורים הללו, האוכלוסייה הייתה גדלה מ -1000 ליותר מ -16 מיליארד חיידקים. כאשר גודל האוכלוסייה, N, משורטט לאורך זמן, נוצרת עקומת צמיחה בצורת J (איור \(\PageIndex{1}\) א).

    הדוגמה של חיידקים בבקבוק אינה מייצגת באמת את העולם האמיתי שבו המשאבים בדרך כלל מוגבלים. עם זאת, כאשר מין מוחדר לבית גידול חדש שנראה לו מתאים, הוא עשוי להראות צמיחה מעריכית לזמן מה. במקרה של החיידקים בבקבוק, חלק מהחיידקים ימותו במהלך הניסוי וכך לא יתרבו; לפיכך, קצב הגידול יורד מקצב מקסימלי בו אין תמותה. קצב הגידול של אוכלוסייה נקבע במידה רבה על ידי הפחתת שיעור התמותה, ד, (מספר אורגניזמים שמתים במרווח) משיעור הילודה, ב, (מספר אורגניזמים שנולדים במרווח). קצב הצמיחה יכול לבוא לידי ביטוי במשוואה פשוטה המשלבת את שיעורי הילודה והתמותה לגורם יחיד: r. זה מוצג בנוסחה הבאה:

    \[\text{Population growth} = rN \nonumber\]

    הערך של r יכול להיות חיובי, כלומר האוכלוסייה גדלה בגודלה (קצב השינוי חיובי); או שלילי, כלומר האוכלוסייה יורדת בגודלה; או אפס, ובמקרה זה גודל האוכלוסייה אינו משתנה, מצב המכונה גידול אוכלוסייה אפס.

    צמיחה לוגיסטית

    צמיחה מעריכית מורחבת אפשרית רק כאשר קיימים משאבי טבע אינסופיים; זה לא המקרה בעולם האמיתי. צ'ארלס דרווין זיהה עובדה זו בתיאורו של "מאבק הקיום", הקובע כי אנשים יתחרו (עם בני מינים משלהם או אחרים) על משאבים מוגבלים. המצליחים נוטים יותר לשרוד ולהעביר את התכונות שגרמו להם להצליח לדור הבא בקצב גדול יותר (ברירה טבעית). כדי לדגמן את המציאות של משאבים מוגבלים, אקולוגים של אוכלוסיות פיתחו את מודל הצמיחה הלוגיסטי.

    כושר נשיאה והמודל הלוגיסטי

    בעולם האמיתי, עם המשאבים המוגבלים שלו, הצמיחה האקספוננציאלית לא יכולה להימשך ללא הגבלת זמן. צמיחה אקספוננציאלית עשויה להתרחש בסביבות שבהן יש מעט פרטים ומשאבים בשפע, אך כאשר מספר הפרטים יגדל מספיק, המשאבים יתדלדלו וקצב הצמיחה יאט. בסופו של דבר, קצב הצמיחה יתיישר או יתיישר (איור \(\PageIndex{1}\) ב). גודל אוכלוסייה זה, הנקבע על פי גודל האוכלוסייה המרבי שסביבה מסוימת יכולה לקיים, נקרא כושר הנשיאה, או K. באוכלוסיות אמיתיות, אוכלוסייה הולכת וגדלה עולה לעתים קרובות על כושר הנשיאה שלה, ושיעור התמותה עולה מעבר לשיעור הילודה וגורם לגודל האוכלוסייה לרדת בחזרה לכושר הנשיאה או מתחתיו. רוב האוכלוסיות בדרך כלל משתנות סביב כושר הנשיאה בצורה גלית ולא קיימות ממש בה.

    הנוסחה המשמשת לחישוב צמיחה לוגיסטית מוסיפה את כושר הנשיאה ככוח ממתן בקצב הצמיחה. הביטוי "K - N" שווה למספר הפרטים שניתן להוסיף לאוכלוסייה בזמן נתון, ו- "K - N" חלקי "K" הוא החלק של כושר הנשיאה הזמין לצמיחה נוספת. לפיכך, מודל הצמיחה האקספוננציאלי מוגבל על ידי גורם זה ליצירת משוואת הצמיחה הלוגיסטית:

    \[\text{Population growth} = rN \left[\dfrac{K-N}{K}\right] \nonumber\]

    שימו לב שכאשר N כמעט אפס הכמות בסוגריים כמעט שווה ל- 1 (או K/K) והצמיחה קרובה לאקספוננציאלית. כאשר גודל האוכלוסייה שווה לכושר הנשיאה, או N = K, הכמות בסוגריים שווה לאפס והצמיחה שווה לאפס. גרף של משוואה זו (צמיחה לוגיסטית) מניב את העקומה בצורת S (איור \(\PageIndex{1}\) ב). זהו מודל מציאותי יותר של גידול אוכלוסייה מאשר גידול מעריכי. ישנם שלושה חלקים שונים לעקומה בצורת S. בתחילה, הצמיחה היא אקספוננציאלית מכיוון שיש מעט אנשים ומשאבים רבים זמינים. ואז, ככל שהמשאבים מתחילים להיות מוגבלים, קצב הצמיחה יורד. לבסוף, קצב הגידול מתיישר בכושר הנשיאה של הסביבה, עם מעט שינוי במספר האוכלוסייה לאורך זמן.

    גם הגרפים (א) וגם (ב) משרטטים את גודל האוכלוסייה לעומת הזמן. בגרף (א), צמיחה אקספוננציאלית גורמת לעקומה שהופכת תלולה יותר ויותר, וכתוצאה מכך צורת J. בגרף (ב), צמיחה לוגיסטית מביאה לעקומה שהופכת תלולה יותר ויותר, ואז יורדת כאשר מגיעים לכושר הנשיאה, וכתוצאה מכך צורת S.
    איור\(\PageIndex{1}\): כאשר המשאבים אינם מוגבלים, אוכלוסיות מציגות (א) צמיחה מעריכית, המוצגת בעקומה בצורת J. כאשר המשאבים מוגבלים, אוכלוסיות מציגות (ב) צמיחה לוגיסטית. בצמיחה לוגיסטית, התרחבות האוכלוסייה פוחתת ככל שהמשאבים נעשים נדירים, והיא מתיישרת כאשר מגיעים לכושר הנשיאה של הסביבה. עקומת הצמיחה הלוגיסטית היא בצורת S.

    תפקיד התחרות הבין-ספציפית

    המודל הלוגיסטי מניח שלכל פרט בתוך אוכלוסייה תהיה גישה שווה למשאבים, ובכך סיכוי שווה להישרדות. עבור צמחים, כמות המים, אור השמש, החומרים המזינים והמרחב לגדול הם המשאבים החשובים, בעוד שבבעלי חיים, משאבים חשובים כוללים מזון, מים, מחסה, מרחב קינון ובני זוג.

    בעולם האמיתי, שונות פנוטיפית בין פרטים בתוך אוכלוסייה פירושה שאנשים מסוימים יותאמו טוב יותר לסביבתם מאחרים. התחרות המתקבלת על משאבים בקרב בני אוכלוסייה מאותו מין נקראת תחרות תוך-ספציפית. תחרות בין-ספציפית עשויה שלא להשפיע על אוכלוסיות הנמצאות הרבה מתחת לכושר הנשיאה שלהן, מכיוון שהמשאבים נמצאים בשפע וכל הפרטים יכולים להשיג את מה שהם צריכים. עם זאת, ככל שגודל האוכלוסייה גדל, התחרות הזו מתעצמת. בנוסף, הצטברות מוצרי פסולת יכולה להפחית את כושר הנשיאה בסביבה.

    דוגמאות לצמיחה לוגיסטית

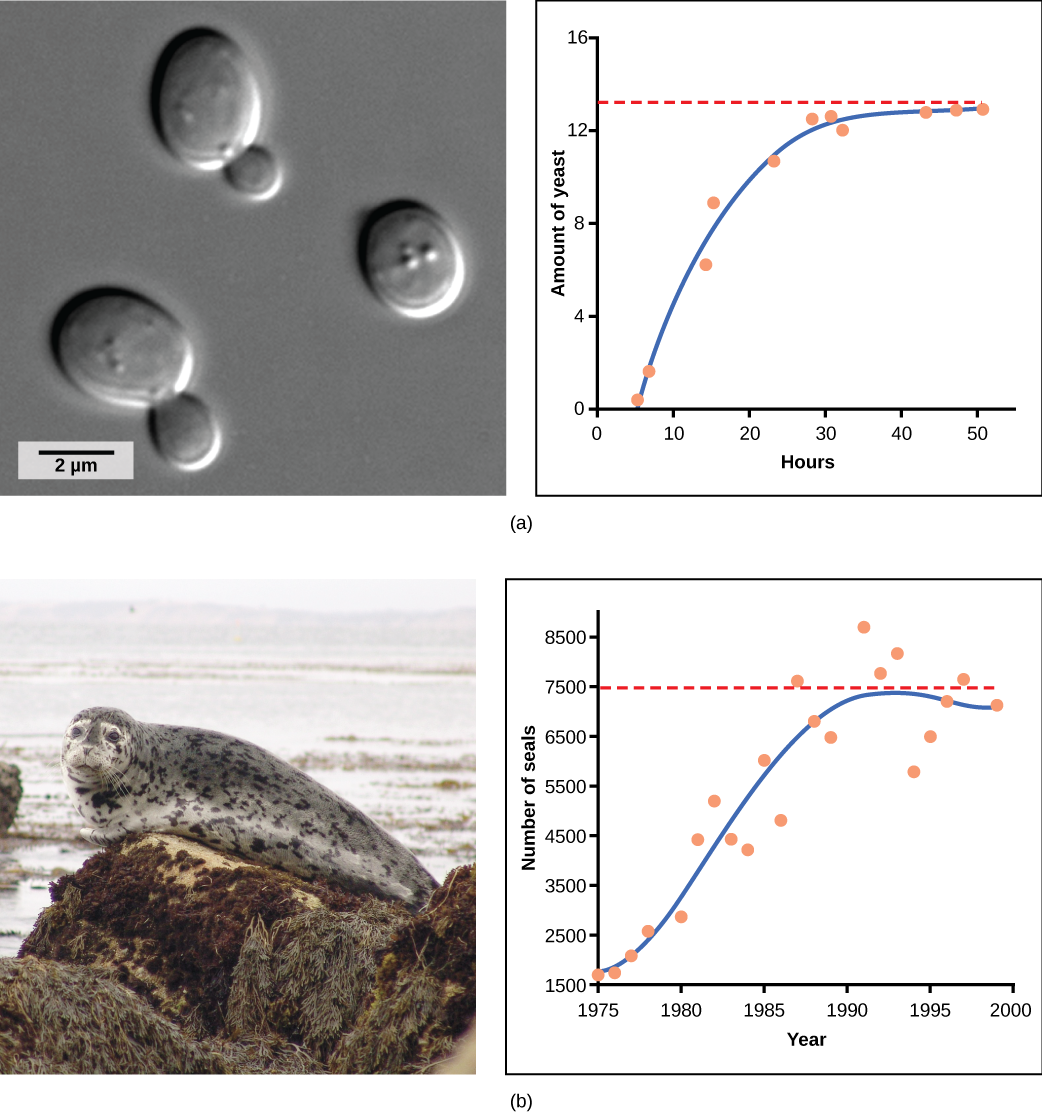
    שמרים, פטרייה מיקרוסקופית המשמשת לייצור לחם ומשקאות אלכוהוליים, מציגה את העקומה הקלאסית בצורת S כאשר היא גדלה במבחנה (איור \(\PageIndex{2}\) א). הצמיחה שלו יורדת ככל שהאוכלוסייה מדלדלת את החומרים המזינים הדרושים לצמיחתה. בעולם האמיתי, לעומת זאת, יש וריאציות לעקומה האידיאלית הזו. דוגמאות באוכלוסיות בר כוללות כבשים וכלבי ים (איור \(\PageIndex{2}\) ב). בשתי הדוגמאות, גודל האוכלוסייה עולה על כושר הנשיאה לפרקי זמן קצרים ואז נופל מתחת לכושר הנשיאה לאחר מכן. תנודה זו בגודל האוכלוסייה ממשיכה להתרחש כאשר האוכלוסייה מתנדנדת סביב כושר הנשיאה שלה. ובכל זאת, אפילו עם תנודה זו, המודל הלוגיסטי מאושר.

    חיבור אמנות

    גרף (א) משרטט את כמות השמרים לעומת זמן הצמיחה בשעות. העקומה עולה בתלילות, ואז מישורית בכושר הנשיאה. נקודות נתונים עוקבות בחוזקה אחר העקומה. גרף (ב) משרטט את מספר חותמות הנמל לעומת הזמן בשנים. שוב, העקומה עולה בתלילות ואז מישורית בכושר הנשיאה, אך הפעם יש הרבה יותר פיזור בנתונים. מיקרוגרף של תאי שמרים, שהם בצורת אליפסה, ותצלום של חותם נמל מוצגים.
    איור\(\PageIndex{2}\): (א) שמרים הגדלים בתנאים אידיאליים במבחנה מציגים עקומת צמיחה לוגיסטית קלאסית בצורת S, ואילו (ב) אוכלוסייה טבעית של כלבי ים מציגה תנודות בעולם האמיתי. השמרים מדמיינים באמצעות מיקרוגרפיה של אור ניגודיות הפרעות דיפרנציאליות. (אשראי א: נתוני סרגל קנה מידה מאת מאט ראסל)

    אם מקור המזון העיקרי של כלבי הים יורד עקב זיהום או דיג יתר, איזה מהבאים צפוי להתרחש?

    1. כושר הנשיאה של כלבי הים יקטן, וכך גם אוכלוסיית החותמות.
    2. כושר הנשיאה של כלבי הים יקטן, אך אוכלוסיית כלבי הים תישאר זהה.
    3. מספר מקרי המוות של כלבי הים יגדל, אך גם מספר הלידות יגדל, כך שגודל האוכלוסייה יישאר זהה.
    4. כושר הנשיאה של כלבי הים יישאר זהה, אך אוכלוסיית כלבי הים תפחת.

    דינמיקת אוכלוסייה ורגולציה

    המודל הלוגיסטי של גידול האוכלוסייה, למרות שהוא תקף באוכלוסיות טבעיות רבות ומודל שימושי, הוא פישוט של דינמיקת האוכלוסייה בעולם האמיתי. המשתמע במודל הוא שיכולת הנשיאה של הסביבה אינה משתנה, וזה לא המקרה. כושר הנשיאה משתנה מדי שנה. לדוגמה, חלק מהקיצים חמים ויבשים ואילו אחרים קרים ורטובים; באזורים רבים כושר הנשיאה במהלך החורף נמוך בהרבה מאשר בקיץ. כמו כן, אירועים טבעיים כמו רעידות אדמה, הרי געש ושריפות יכולים לשנות סביבה ומכאן כושר הנשיאה שלה. בנוסף, אוכלוסיות בדרך כלל אינן קיימות בבידוד. הם חולקים את הסביבה עם מינים אחרים, ומתחרים בהם על אותם משאבים (תחרות בין-ספציפית). גורמים אלה חשובים גם להבנת האופן שבו אוכלוסייה ספציפית תגדל.

    גידול האוכלוסייה מוסדר במגוון דרכים. אלה מקובצים לגורמים תלויי צפיפות, בהם צפיפות האוכלוסייה משפיעה על קצב הגידול והתמותה, וגורמים בלתי תלויים בצפיפות, הגורמים לתמותה באוכלוסייה ללא קשר לצפיפות האוכלוסייה. ביולוגים של חיות בר, במיוחד, רוצים להבין את שני הסוגים מכיוון שזה עוזר להם לנהל אוכלוסיות ולמנוע הכחדה או אוכלוסיית יתר.

    תקנה תלויה בצפיפות

    רוב הגורמים התלויים בצפיפות הם ביולוגיים באופיים וכוללים טריפה, תחרות בין-תוך-ספציפית וטפילים. בדרך כלל, ככל שהאוכלוסייה צפופה יותר, כך שיעור התמותה שלה גדול יותר. לדוגמה, במהלך תחרות תוך-ובין-ספציפית, שיעורי הרבייה של המינים יהיו בדרך כלל נמוכים יותר, מה שמפחית את קצב הגידול של אוכלוסייתם. בנוסף, צפיפות טרף נמוכה מגדילה את התמותה של הטורף שלו מכיוון שהוא מתקשה יותר לאתר את מקור המזון שלו. כמו כן, כאשר האוכלוסייה צפופה יותר, מחלות מתפשטות במהירות רבה יותר בקרב בני האוכלוסייה, המשפיעות על שיעור התמותה.

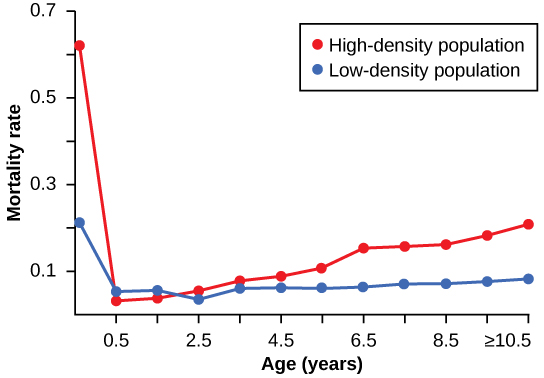
    ויסות תלוי צפיפות נחקר בניסוי טבעי עם אוכלוסיות חמורי בר בשני אתרים באוסטרליה. 1 באתר אחד האוכלוסייה צומצמה על ידי תוכנית לבקרת אוכלוסין; האוכלוסייה באתר השני לא קיבלה שום הפרעה. העלילה בצפיפות גבוהה הייתה צפופה פי שניים מהעלילה בצפיפות נמוכה. בין השנים 1986 ל -1987 העלילה בצפיפות גבוהה לא ראתה שינוי בצפיפות החמור, ואילו העלילה בצפיפות נמוכה ראתה עלייה בצפיפות החמור. ההבדל בשיעורי הגידול של שתי האוכלוסיות נגרם כתוצאה מתמותה, ולא מהבדל בשיעורי הילודה. החוקרים מצאו שמספר הצאצאים שנולדו על ידי כל אם לא הושפע מצפיפות. שיעורי הגידול בשתי האוכלוסיות היו שונים בעיקר בגלל תמותת נעורים שנגרמה כתוצאה מתת תזונה של האם עקב מזון דל באיכות גבוהה באוכלוסייה הצפופה. איור \(\PageIndex{3}\) מראה את ההבדל בתמותה ספציפית לגיל בשתי האוכלוסיות.

    גרף עם שיעור תמותה מ 0 עד 0.7 על ציר Y וגיל בשנים מ 0 עד גדול או שווה ל 10.5 על ציר X. שיעור התמותה של האוכלוסייה בצפיפות גבוהה מתחיל בערך 0.6 בגיל 0 (סמוך ללידה) ואז יורד באופן דרמטי לכ -0.03 בגיל שישה חודשים, ואז מטפס בקו כמעט ישר ומגיע לכ -0.2 בגיל 10.5 שנים. שיעור התמותה באוכלוסייה בצפיפות נמוכה מתחיל בערך 0.2 בגיל 0 (סמוך ללידה) ואז יורד לכ -0.06 בגיל שישה חודשים, ואז מטפס בהדרגה רק בכמות קטנה ומגיע לכ 0.1 בגיל 10.5 שנים.
    איור\(\PageIndex{3}\): גרף זה מציג את שיעורי התמותה הספציפיים לגיל עבור חמורי בר מאוכלוסיות בצפיפות גבוהה ונמוכה. תמותת הנעורים גבוהה בהרבה באוכלוסייה בצפיפות גבוהה בגלל תת תזונה אימהית הנגרמת על ידי מחסור במזון איכותי.

    ויסות בלתי תלוי בצפיפות ואינטראקציה עם גורמים תלויי צפיפות

    גורמים רבים שהם בדרך כלל פיזיים באופיים גורמים לתמותה של אוכלוסייה ללא קשר לצפיפותה. גורמים אלה כוללים מזג אוויר, אסונות טבע וזיהום. צבי בודד ייהרג בשריפת יער ללא קשר לכמה צבאים נמצאים באזור זה. סיכויי ההישרדות שלה זהים בין אם צפיפות האוכלוסייה גבוהה או נמוכה. הדבר נכון גם לגבי מזג אוויר חורפי קר.

    במצבים אמיתיים, ויסות האוכלוסייה מסובך מאוד וגורמים תלויי צפיפות ועצמאיים יכולים לקיים אינטראקציה. אוכלוסייה צפופה הסובלת מתמותה מסיבה בלתי תלויה בצפיפות תוכל להתאושש באופן שונה מאוכלוסייה דלילה. לדוגמה, אוכלוסיית צבאים שנפגעו מחורף קשה תתאושש מהר יותר אם יישארו עוד צבאים להתרבות.

    אבולוציה בפעולה: מדוע הממותה הצמרית נכחדה?

    תמונה (א) מציגה ציור של ממותות שהולכות בשלג. תמונה (ב) מציגה ממותה ממותה יושבת בתוך ויטרינה במוזיאון. תמונה (ג) מציגה ממותה תינוקת חנוטה, גם היא בוויטרינה.
    איור\(\PageIndex{4}\): שלוש התמונות כוללות: (א) ציור קיר משנת 1916 של עדר ממותה מהמוזיאון האמריקאי להיסטוריה של הטבע, (ב) הממותה הממולאת היחידה בעולם נמצאת במוזיאון לזואולוגיה הממוקם בסנט פטרסבורג, רוסיה, ו- (ג) ממותה תינוקת בת חודש, בשם ליובה, שהתגלתה בסיביר בשנת 2007. (אשראי א: שינוי עבודה מאת צ'ארלס ר 'נייט; קרדיט ב: שינוי עבודה על ידי "Tanapon" /Flickr; אשראי ג: שינוי העבודה על ידי מאט האורי)

    ממותות צמר החלו להיכחד לפני כ -10,000 שנה, זמן קצר לאחר שהפליאונטולוגים מאמינים שבני אדם המסוגלים לצוד אותם החלו ליישב את צפון אמריקה וצפון אירואסיה (איור). \(\PageIndex{4}\) אוכלוסיית ממותה שרדה באי ורנגל, בים הסיבירי המזרחי, והייתה מבודדת ממגע אנושי עד לאחרונה בשנת 1700 לפני הספירה. אנו יודעים הרבה על בעלי חיים אלה מפגרים שנמצאו קפואים בקרח סיביר ובאזורים צפוניים אחרים.

    מקובל לחשוב ששינויי אקלים וציד אנושי הובילו להכחדתם. מחקר משנת 2008 העריך כי שינויי האקלים הפחיתו את טווח הממותה מ -3,000,000 קילומטרים רבועים לפני 42,000 שנה ל -310,000 קילומטרים רבועים לפני 6,000 שנה. 2 באמצעות עדויות ארכיאולוגיות לאתרי הרג, מתועד היטב שבני אדם צדו את החיות הללו. מחקר שנערך בשנת 2012 הגיע למסקנה כי אף גורם אחד אינו אחראי באופן בלעדי להכחדת היצורים המפוארים הללו. 3 בנוסף לשינויי האקלים וצמצום בתי הגידול, מדענים הוכיחו גורם חשוב נוסף בהכחדת הממותה היה נדידת ציידים אנושיים על פני מיצר ברינג לצפון אמריקה בתקופת הקרח האחרונה לפני 20,000 שנה.

    שמירה על אוכלוסיות יציבות הייתה ומורכבת מאוד, כאשר גורמים רבים באינטראקציה קובעים את התוצאה. חשוב לזכור שגם בני האדם הם חלק מהטבע. פעם תרמנו לירידה של מין באמצעות טכנולוגיית ציד פרימיטיבית בלבד.

    מודלים של אוכלוסייה מבוססת דמוגרפיה

    אקולוגים של אוכלוסיות שיערו כי חבילות מאפיינים עשויות להתפתח במינים המובילים להתאמות מסוימות לסביבתם. התאמות אלה משפיעות על סוג גידול האוכלוסייה שהמינים שלהם חווים. מאפייני היסטוריית החיים כמו שיעורי ילודה, גיל בהתרבות ראשונה, מספר הצאצאים ואפילו שיעורי התמותה מתפתחים בדיוק כמו אנטומיה או התנהגות, מה שמוביל להתאמות המשפיעות על גידול האוכלוסייה. אקולוגים של אוכלוסיות תיארו רצף של "אסטרטגיות" היסטוריות חיים עם מינים שנבחרו K בקצה אחד ומינים נבחרים r בצד השני. K -מינים נבחרים מותאמים לסביבות יציבות וצפויות. אוכלוסיות של מינים נבחרים K נוטות להתקיים קרוב ליכולת הנשיאה שלהן. מינים אלה נוטים להיות בעלי צאצאים גדולים יותר, אך פחותים, ותורמים כמויות גדולות של משאבים לכל צאצא. פילים יהיו דוגמה למין שנבחר K. מינים נבחרים r מותאמים לסביבות לא יציבות ובלתי צפויות. יש להם מספר גדול של צאצאים קטנים. בעלי חיים שנבחרו r אינם מספקים משאבים רבים או טיפול הורי לצאצאים, והצאצאים עצמאיים יחסית בלידה. דוגמאות למינים שנבחרו r הם חסרי חוליות ימיים כגון מדוזות וצמחים כגון שן הארי. שתי האסטרטגיות הקיצוניות נמצאות בשני קצוות של רצף שעליו יתקיימו היסטוריות חיים של מינים אמיתיים. בנוסף, אסטרטגיות היסטוריית החיים אינן צריכות להתפתח כסוויטות, אלא יכולות להתפתח ללא תלות זו בזו, כך שלכל מין עשויים להיות מאפיינים מסוימים המתמקדים בקיצוניות כזו או אחרת.

    סיכום המדור

    אוכלוסיות עם משאבים בלתי מוגבלים גדלות באופן אקספוננציאלי - עם קצב צמיחה מואץ. כאשר המשאבים הופכים מגבילים, אוכלוסיות עוקבות אחר עקומת גידול לוגיסטית שבה גודל האוכלוסייה יתיישר בכושר הנשיאה.

    אוכלוסיות מוסדרות על ידי מגוון גורמים תלויי צפיפות ובלתי תלויים בצפיפות. מאפייני היסטוריית חיים, כגון גיל בהתרבות ראשונה או מספר צאצאים, הם מאפיינים המתפתחים באוכלוסיות בדיוק כפי שאנטומיה או התנהגות יכולים להתפתח עם הזמן. המודל של r - ו- K -selection מצביע על כך שתווים, ואולי סוויטות של תווים, עשויים לפתח התאמות ליציבות האוכלוסייה בסמוך ליכולת הנשיאה (K -selection) או גידול והתמוטטות אוכלוסייה מהירה (r -בחירה). מינים יציגו התאמות איפשהו על רצף בין שני הקצוות הללו.

    תרגיל אמנות

    איור\(\PageIndex{2}\): אם מקור המזון העיקרי של כלבי הים יורד עקב זיהום או דיג יתר, איזה מהבאים צפוי להתרחש?

    1. כושר הנשיאה של כלבי הים יקטן, וכך גם אוכלוסיית החותמות.
    2. כושר הנשיאה של כלבי הים יקטן, אך אוכלוסיית כלבי הים תישאר זהה.
    3. מספר מקרי המוות של כלבי הים יגדל, אך גם מספר הלידות יגדל, כך שגודל האוכלוסייה יישאר זהה.
    4. כושר הנשיאה של כלבי הים יישאר זהה, אך אוכלוסיית כלבי הים תפחת.
    תשובה

    ת: כושר הנשיאה של כלבי הים יקטן, וכך גם אוכלוסיית החותמות.

    הערות שוליים

    1. 1 דיוויד צ'וקנו, "צמיחה תלויה בצפיפות, מצב גוף ודמוגרפיה בחמורים פראיים: בדיקת השערת המזון" אקולוגיה 72, מס '3 (יוני 1991): 805—813.
    2. 2 דיוויד נוגה-בראבו ואח ', "שינויי אקלים, בני אדם והכחדת הממותה הצמרית." פלוס ביול 6 (אפריל 2008): e79, דוי:10.1371/יומן. pbio.0060079.
    3. 3 GM מקדונלד ואח ', "דפוס ההכחדה של הממותה הצמרית בברינגיה". תקשורת טבע 3, מס '893 (יוני 2012), דוי:10.1038/ncomms1881.

    רשימת מילים

    שיעור הילודה
    מספר הלידות בתוך אוכלוסייה בנקודת זמן מסוימת
    כושר נשיאה
    המספר המרבי של פרטים באוכלוסייה שניתן לתמוך במשאבים המוגבלים של בית גידול
    שיעור תמותה
    מספר מקרי המוות בתוך אוכלוסייה בנקודת זמן מסוימת
    ויסות תלוי צפיפות
    ויסות האוכלוסייה שבה שיעורי הילודה והתמותה תלויים בגודל האוכלוסייה
    תקנה בלתי תלויה בצפיפות
    הסדרת האוכלוסייה שבה שיעור התמותה אינו תלוי בגודל האוכלוסייה
    צמיחה מעריכית
    דפוס צמיחה מואץ שנראה באוכלוסיות בהן המשאבים אינם מגבילים
    תחרות לא ספציפית
    התחרות בין בני אותו המין
    עקומת צמיחה בצורת J
    צורה של עקומת צמיחה אקספוננציאלית
    K -מינים נבחרים
    מין המתאים לסביבות יציבות המייצרות כמה צאצאים גדולים יחסית ומספקים טיפול הורי
    צמיחה לוגיסטית
    פילוס הצמיחה האקספוננציאלית עקב הגבלת משאבים
    r -מינים נבחרים
    מין המתאים לסביבות משתנות המייצרות צאצאים רבים ומספקים טיפול הורי מועט או ללא טיפול הורי
    עקומת צמיחה בצורת S
    צורת עקומת צמיחה לוגיסטית
    גידול אוכלוסייה אפסי
    גודל האוכלוסייה היציב שבו שיעורי הילודה ושיעורי התמותה שווים

    תורמים וייחוסים