1.4: בעיות סיכום

Last updated
Save as PDF

Page ID: 208303

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

1.4 בעיות סיכום

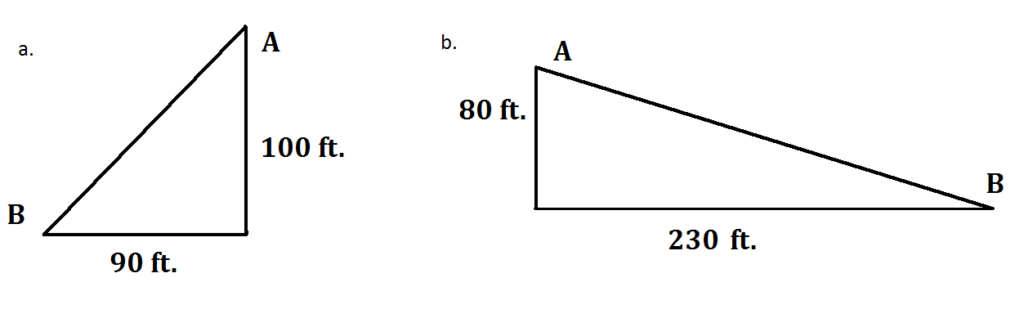
1. בעזרת המדידות שסופקו, קבע את אחוז השיפוע של המדרונות הבאים בין נקודות A ו- B.

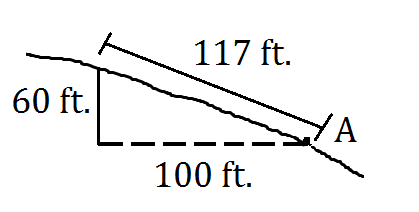
2. במדרון של 60%, טוד רוצה לעלות במדרון מרחק שווה ערך למרחק אופקי של 100 רגל. כמה רחוק הוא צריך ללכת מנקודה A?

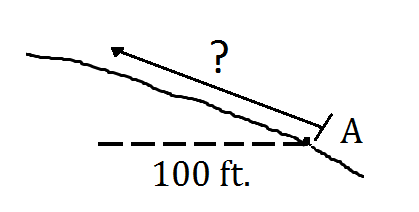
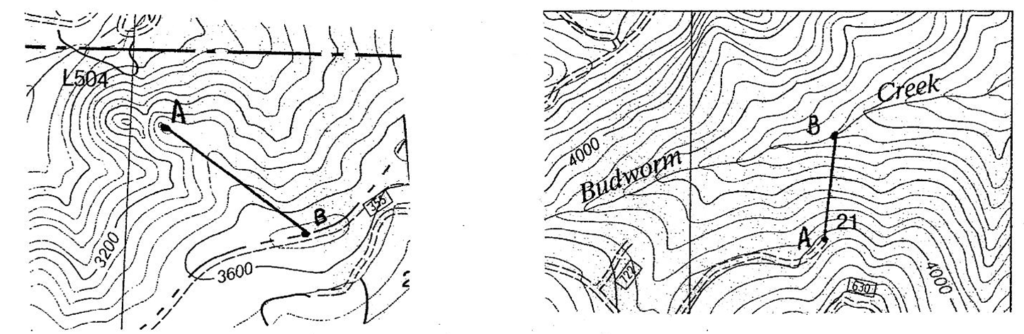
3. במפות קווי המתאר שלהלן, קבע את השיפועים הממוצעים בין נקודות A ו- B. הסולם הוא 1 "= 2000'. מרווח קווי המתאר הוא 80 '.

תשובות לשאלות סיכום

1. 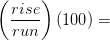% שיפוע

1 א. 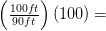111%

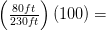1 ב. 35%

2. במדרון של 60% אנו יודעים שהעלייה היא 60% מהריצה. לכן, העלייה כאן צריכה להיות 60% של 100 רגל או 60 רגל. באמצעות משפט פיתגורס, אנו יכולים לפתור עבור hypotenuse.

א ² + ב ² = ג ² איפה:

100 ² + 60 ² = ג ²

^{13,600 = ג 2}

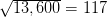רגל.

3. התשובות לשאלות אלה יהיו תלויות באופן שבו מדדת את המרחק האופקי, או המפה - קשה לעשות על המסך. המידות שלי מוצגות במפות למטה:

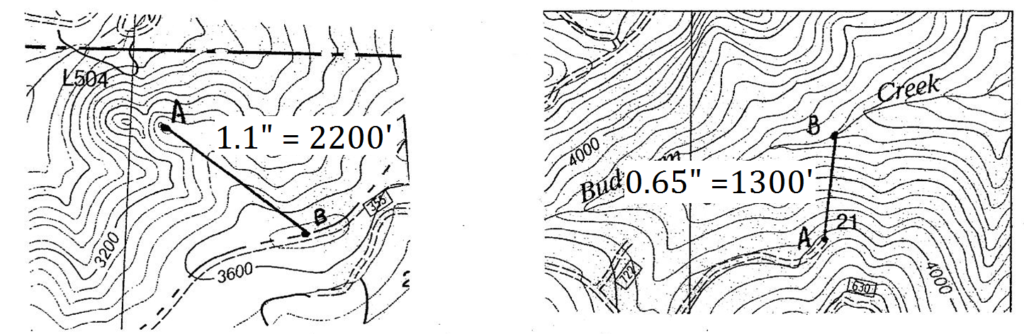
בצד שמאל. נקודה א 'היא ≈ 3440 '. נקודה B היא ≈ 3720 '. העלייה היא 280 '. הריצה היא ≈ 2200 '. לכן השיפוע הממוצע הוא (280) (100) /2200 = 13%.

בצד ימין. נקודה א 'היא ≈ 4040 '. נקודה B היא ≈ 3280 '. העלייה היא 760 '. הריצה היא 1300 '. לכן השיפוע הממוצע הוא (760) (100) /2200 = 58%