4.12: Mifano ya Matumizi ya Kazi
- Page ID
- 164674
Mifano iliyowekwa ya kazi (matatizo ya neno la AKA!) inaweza kuchukua aina nyingi.
Kuwa tayari kutumia aina yoyote ya kazi ambayo imekuwa upya katika sura hii.
Kazi ya majira ya joto hulipa muda na nusu kwa muda wa ziada ikiwa mfanyakazi anafanya kazi zaidi ya masaa 40. Baada ya masaa 40, mfanyakazi hulipwa mara 1.5 kiwango cha saa\($12.00\) kwa saa.
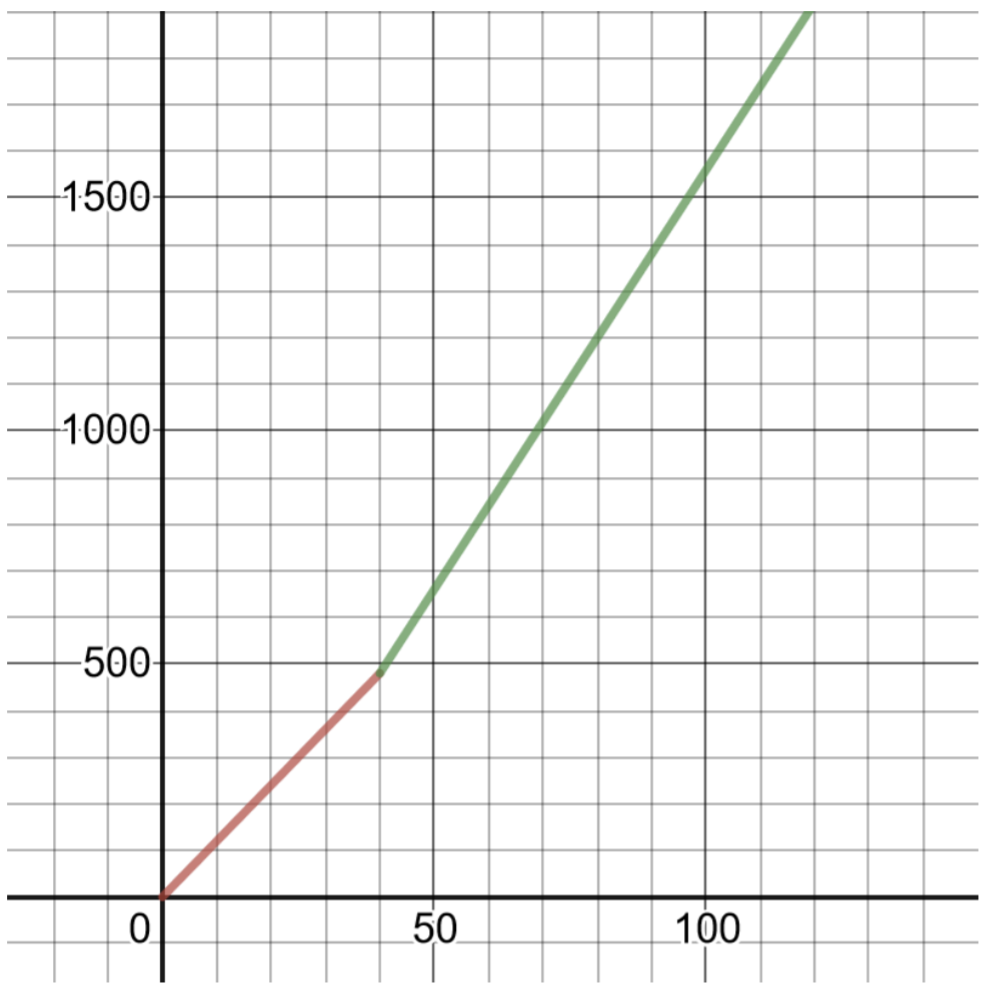
- Andika na graph kipande busara kazi ambayo inatoa kila wiki kulipa P katika suala la idadi ya masaa kazi h. hint: Hii inaweza kuwa gumu, fikiria jinsi ya kueleza idadi ya masaa juu ya 40.
- Kiasi gani itakuwa chuma kazi masaa 45?
Suluhisho
- Kuandika kazi ya busara ya kipande:
\(P (h) = \left\{\begin{array}{cc} 12h &0 < h \leq 40 \\ 12(40) + 1.5(12)(h − 40) &h > 40\end{array} \right.\)
Ili kuchora kazi hii, fanya meza ya ufumbuzi:
|
Jedwali la Solutions kwa\(P (h) = 12h \) Domain\(0 < h \leq 40\) |
|
| \(h\) | \(P(h)\) |
| 1 | \($12.00\) |
| 10 | \($120.00\) |
| 40 | \($480.00\) |
|
Jedwali la Solutions kwa\(P (h) = 12(40) + 1.5(7)(h − 40) \) Rahisi\(P (h) = 18h − 240 \) Domain\(h > 40\) |
|
| \(h\) | \(P(h)\) |
| 41 | 498 |
| 45 | 570 |
| 50 | 660 |
| 60 | 840 |
- \($570.00\)kwa masaa 45 ya kazi (angalia Jedwali la Solutions)
NASA yazindua roketi kwa\(t=0\) sekunde. Urefu wake, katika mita juu ya usawa wa bahari, kama kazi ya muda hutolewa na\(h(t) = −4.9t^2 + 46t + 227\).
- Kutokana kwamba roketi itakuwa Splash chini ndani ya bahari, wakati gani splashdown kutokea?
- Je, roketi hupata kilele gani juu ya usawa wa bahari?
Suluhisho
- Wakati Splash chini\(h(t) = 0\),, hivyo kuweka kazi sawa na 0 na kutatua kwa\(t\).
\(0 = −4.9t 2 + 46t + 227\)
Tumia Mfumo wa Quadratic kutatua equation hii\(a = −4.9\), na\(b = 46\),\(c = 227\)
\(\begin{aligned} t &= \dfrac{−46 \pm \sqrt{46^2 − 4(−4.9)(227) }}{2(−4.9) } && \text{Quadratic Formula} \\ t &= \dfrac{−46 \pm \sqrt{ 2116 + 4449.2 }}{−9.8 } &&\text{Simplify the radical} \\ t &= \dfrac{46 \pm \sqrt{ 6565.2 }}{9.8 } &&\text{Further simplify the radical, divide all terms by -1 (still have } \pm\text{ )} \\t &= \dfrac{46 \pm 81.026 }{9.8 } &&\text{Square root} \\ t &= \dfrac{46 + 81.026 }{9.8 } &&\text{Addition} \\ t &= \dfrac{46 − 81.026 }{9.8} && \text{Subtraction} \\ t& = 12.96 \text{ and } t = −3.57&& \text{Two solutions, reject negative solution because time cannot be negative} \\ t &= 12.96 \text{ seconds }&&\text{Final Answer} \end{aligned}\)
- Je, roketi hupata kilele gani juu ya usawa wa bahari?
Ishara ya mgawo wa muda wa kuongoza wa kazi ya quadratic\(h(t) = −4.9t^2 + 46t + 227\) inaonyesha njia gani parabola inafungua. Mgawo ni\(−4.9\), na kwa kuwa ni hasi, kazi ya quadratic inafungua chini.
Sasa tunahitaji kupata vertex. Thamani ya y ya jozi iliyoamriwa ya vertex itaonyesha ambapo upeo huanza.
Vertex ni\(\left(− \dfrac{b }{2a} , f\left( −\dfrac{ b }{2a}\right) \right)\), pamoja\(a = −4.9\) na\(b = 46\)
Kipeo ni\(\left(−\dfrac{ 46 }{2(−4.9) }, f\left( − \dfrac{46 }{2(−4.9)}\right)\right)\)
Vertex ni\((4.694, f (4.694))\) ambayo ni\((4.694, (−4.9)(4.694)^2 + (46)(4.694) + 227 ))\) au\((4.694, 334.959)\)
Urefu wa roketi kwenye kilele chake ni\(334.959\) mita juu ya usawa wa bahari.
Ili kukuza mauzo ya kikundi kwa cruise ya Alaskan, shirika la usafiri hupunguza bei ya tiketi ya mara\($4500\)\($5\) kwa mara ya kila mtu katika kikundi.
- Andika equation linear kwamba anatoa gharama kwa kila mtu\(f(p)\), kama\(p\) watu kusafiri katika kundi.
- Tumia equation kuamua gharama kwa watu 50.
Suluhisho
- Kwa kuwa gharama ya kila mtu imepungua kiasi sawa kwa kila mtu, hii ni equation linear.
Tumia\(f(x) = mx + b\), au hebu tuandike kama\(f(p) = mp + b\), kwa gharama\(f(p)\) ya kila mtu.
\(f(p) = mp + b\)
Kwa kuwa gharama ya kila mtu imepungua kwa $5 kwa kila mtu katika kikundi, hiyo ni mteremko wa mstari.
\(\begin{aligned} f(p)&= −5p + b && \text{Slope-intercept form of the equation of a line} \\ f(p) &= −5p + 4500 &&\text{The y-intercept is the starting point, so the regular ticket price of }$4500 {is the y-intercept} \\ f(p)& = −5p + 4500 && \text{Linear Equation} \end{aligned}\)
- Tumia equation kuamua gharama kwa watu 50.
\(\begin{aligned} f(50) &= −5(50) + 4500 && \text{Replace p with 50 people in the Linear Equation} \\ f(50) &= −250 + 4500 &&\text{Simplify} \\ f(50) &= 4250 &&\text{Simplify} \\ \text{If }50 &\text{ people take the cruise, the cost per-person for the cruise is } $4250&&\text{Final Answer }\end{aligned}\)
Jaza matatizo yafuatayo ya kazi:
- Mchezaji anashutumu ada ya msingi ya\($20\) pamoja\($5\) kwa barua ili kushona jina la mwanariadha nyuma ya koti.
- Andika equation linear ambayo utapata gharama ya kuwa na jina zenye barua x kushonwa nyuma ya koti.
- Ni gharama gani kwa jina na barua 11?
- Katika Acapulco, Mexico, kivutio maarufu cha utalii ni kuangalia wanaume wakipiga mbizi kutoka mwamba hadi maji 75 miguu chini. Urefu wa diver\(f(t)\) juu ya maji (kwa miguu),\(t\) sekunde baada ya kupiga mbizi, hutolewa na\(f(t) = −16t^2+75\).
- Je! Kupiga mbizi hudumu kwa muda gani?
- Katika nchi fulani, kodi ya mapato ni tathmini kama ifuatavyo: Hakuna kodi ya mapato hadi\($15000\). Mapato tena\($15000\) na hadi\($30000\) ni kujiandikisha katika\(12%\). Mapato zaidi\($30000\) ni kujiandikisha katika\(18%\).
- Andika kazi ya kipande cha habari hapo juu na mchoro grafu yake.
- Kuamua kiasi cha kodi ya kulipwa kwa mapato ya\($18000\).


