Skip to main content
Global

4.11: Kazi ya Ufafanuzi wa Kipande

  1. Last updated
  2. Save as PDF
  • Page ID
    164612

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Ufafanuzi: Kazi zilizoelezwa Kipande

    Kazi zilizoelezwa kwa kipande ni kazi ambazo hufafanuliwa kwa kutumia milinganyo tofauti kwa sehemu tofauti za kikoa.

    Mfano Template:index

    Tathmini zifuatazo piecewise-defined kazi kwa maadili fulani ya\(x\), na graph kazi:

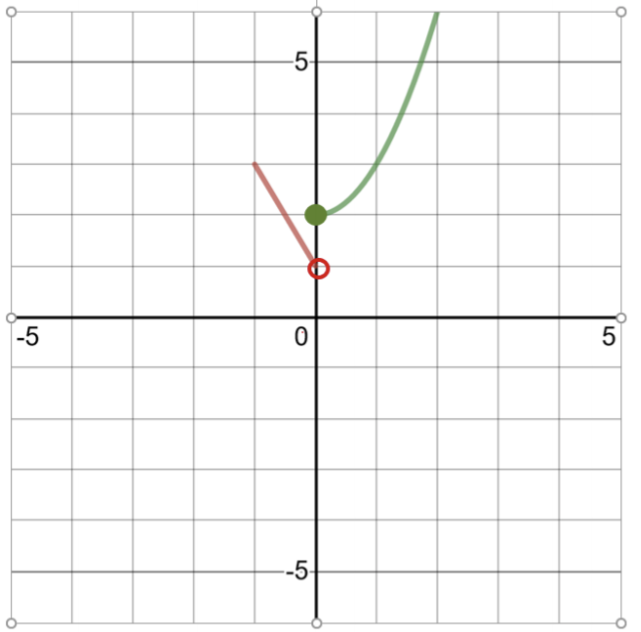
    \(f(x) = \left\{\begin{array}{cc}−2x + 1 & −1 \leq x < 0 \\ x^2 + 2 &0 \leq x \leq 2\end{array} \right.\)

    Suluhisho

    Ili kuchora kazi hii, fanya meza ya ufumbuzi:

    Jedwali la Solutions kwa\(f(x) = −2x + 1 \)

    Domain\(−1 \leq x < 0\)
    \(x\) \(f(x)\)
    -1 3
    0 1 (mduara wazi hapa, 0 si katika uwanja)

    Jedwali la Solutions kwa\(f(x) = x^2 + 2\)

    Domain\(0 \leq x \leq 2\)
    \(x\) \(f(x)\)
    0 2
    1 3
    2 6
    clipboard_e94fd5197718a7373772af1280306cf06.png
    Kielelezo Template:index
    Mfano Template:index

    Tathmini zifuatazo piecewise-defined kazi kwa maadili fulani ya\(x\), na graph kazi:

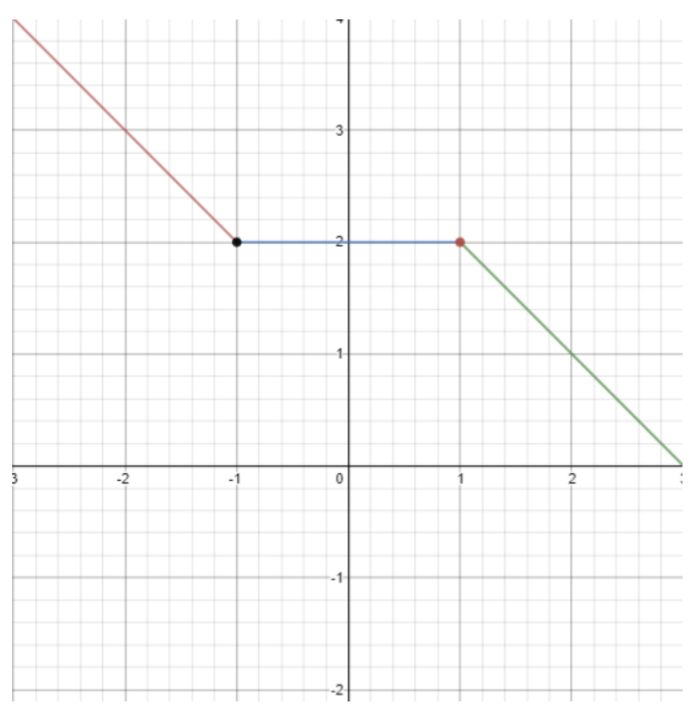
    \(f(x) = \left\{\begin{array}{cc} −x + 1 &x \leq −1 \\ 2 & −1 < x \leq 1 \\ −x + 3 &x > 1 \end{array}\right.\)

    Suluhisho

    Ili kuchora kazi hii, tena ufanye meza ya ufumbuzi:

    Jedwali la Solutions kwa\(f(x) = −x + 1\)

    Domain\(x \leq −1\)
    \(x\) \(f(x)\)
    -3 4
    -2 3
    -1 2 (mduara uliofungwa hapa, -1 iko kwenye kikoa)

    Jedwali la Solutions kwa\(f(x) = 2\)

    Domain\(−1 < x \leq 1\)
    \(x\) \(f(x)\)
    -1 2 (mduara wazi kujazwa na kazi ya awali, -1 si katika uwanja)
    0 2
    1 2 (mduara uliofungwa hapa, 1 iko katika uwanja)

    Jedwali la Solutions kwa\(f(x) = −x + 3\)

    Domain\(x > 1\)
    \(x\) \(f(x)\)
    1 2 (mduara wazi kujazwa na kazi ya awali, 1 si katika uwanja)
    2 1
    3 0
    clipboard_e795cd2fce50083772c8741bdcad72855.png
    Kielelezo Template:index
    Zoezi Template:index

    Tathmini kazi zifuatazo zilizoelezwa kwa kipande kwa maadili yaliyotolewa ya x, na graph kazi:.

    1. \ (f (x) =\ kushoto\ {\ kuanza {safu} {cc}
      x & x<0\\
      2 x+1 &x\ geq 0
      \ mwisho {safu}\ haki.\)
    2. \(g(x) = \left\{\begin{array}{cc} 4 − x& x < 2\\ 2x − 2 &x \geq 2 \end{array} \right.\)
    3. \(h(x) = \left\{\begin{array}{cc} −x − 1 & x < −1 \\ 0& −1 \leq x \leq 1 \\ x + 1 & x > 1 \end{array} \right.\)
    4. \(g(x) = \left\{\begin{array}{cc} 6 & −8 \leq x < −4 \\ 3 &−4 \leq x \leq 5 \end{array}\right.\)
    5. \(f(x) = \left\{\begin{array}{cc} −x + 1 & −1 \leq x < 1 \\ \sqrt{x − 1 } &1 \leq x \leq 5\end{array}\right.\)