Skip to main content
Global

4.5: Kazi kamili ya Thamani

  1. Last updated
  2. Save as PDF
  • Page ID
    164636

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Kwa grafu kazi absolute-thamani, kuchagua maadili ndogo ya\(x\), na compute thamani ya\(f(x)\) kutoka kazi kutokana na kujenga jozi kuamuru. Tatu zilizoamriwa jozi ni kiasi cha chini kinachohitajika ili graph kazi ya thamani kamili. Kuwa makini, kwa sababu jozi moja iliyoamriwa lazima iwakilisha vertex, hatua ambapo pande za kushoto na za kulia za kazi hukutana. Kwa usahihi grafu sura ya kazi ya thamani kabisa, vertex inapaswa kupatikana.

    \(f(x) = a\vert x − h\vert+ k\)Fomu ya jumla ya Kazi ya Thamani kamili, na vertex\((h,k)\)

    • \(a\)huamua upana na mwelekeo (inakabiliwa juu au chini) ya kazi.
    • \(h\)ni mabadiliko ya usawa kutoka kwa asili.
    • \(k\)ni mabadiliko ya wima kutoka kwa asili.

    Anza kwa kutambua jozi iliyoamriwa ya vertex, na kisha kupata jozi moja iliyoamriwa upande wa kushoto wa asili, na kwa haki ya asili. Chagua kitengo cha x-thamani moja upande wa kushoto wa thamani ya x-ya asili, uhesabu\(f(x)\) na kisha uchague kitengo kimoja cha thamani ya x ya asili na uhesabu\(f(x)\). Grafu itafanana\(V\), ama inakabiliwa juu au chini, kulingana na ishara ya\(a\).

    Mfano Template:index

    Unda meza ya ufumbuzi na grafu kazi ya thamani kamili:

    \(f(x) = \vert x − 4\vert\)

    Suluhisho

    Kulinganisha kazi hii kwa fomu ya jumla ya kazi za thamani kamili (iliyoonyeshwa hapo juu),\(a = 1\),\(h = 4\),\(k = 0\). Vertex ni\((h, k)\) au\((4, 0)\).

    Ili kupata mbili zaidi kuamuru jozi, kuchagua\(x = 3\) na\(x = 5\), kisha compute maadili ya\(f(x)\).

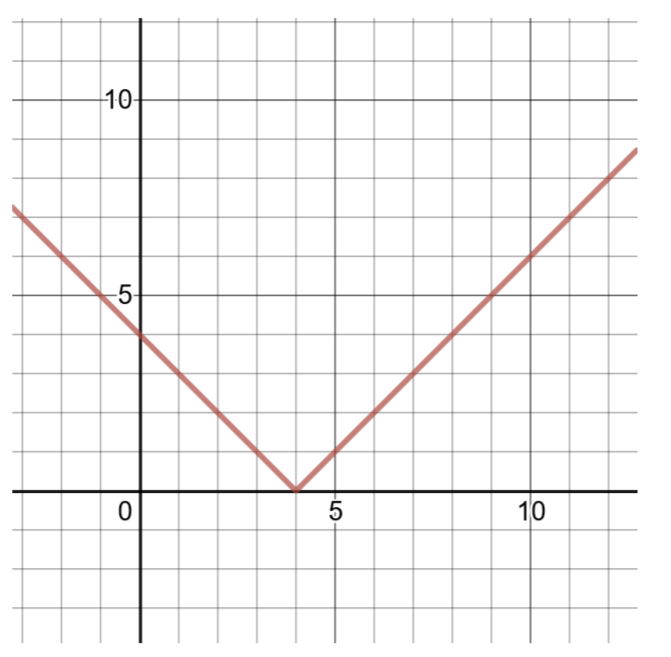
    clipboard_e4c9bfc2e550aa369ba89481f9ab5d4fb.png
    Kielelezo Template:index
    Jedwali la Solutions kwa\(f(x) = \vert x − 4\vert\)
    \(x\) \(f(x)\)
    \ (x\) ">3 \ (f (x)\) ">\(f(3) = \vert 3 − 4\vert = \vert − 1\vert = 1\)
    \ (x\) ">4 \ (f (x)\) ">\(f(4) = \vert 4 − 4\vert = \vert 0\vert = 0\)
    \ (x\) "> 5 \ (f (x)\) ">\(f(5) = \vert 5 − 4\vert = \vert 1\vert = 1\)
    Mfano Template:index

    Unda meza ya ufumbuzi na grafu kazi ya thamani kamili:

    \(g(x) = \vert x + 2\vert − 5\)

    Suluhisho

    Kulinganisha kazi hii kwa fomu ya jumla ya kazi za thamani kamili (iliyoonyeshwa hapo juu),\(a = 1\),\(h = −2\),\(k = −5\). Kipeo ni (h, k)\) au\((−2, −5)\).

    Ili kupata jozi mbili zilizoamriwa, chagua\(x = −3\) na\(x = −1\), kisha uhesabu maadili ya\(g(x)\)

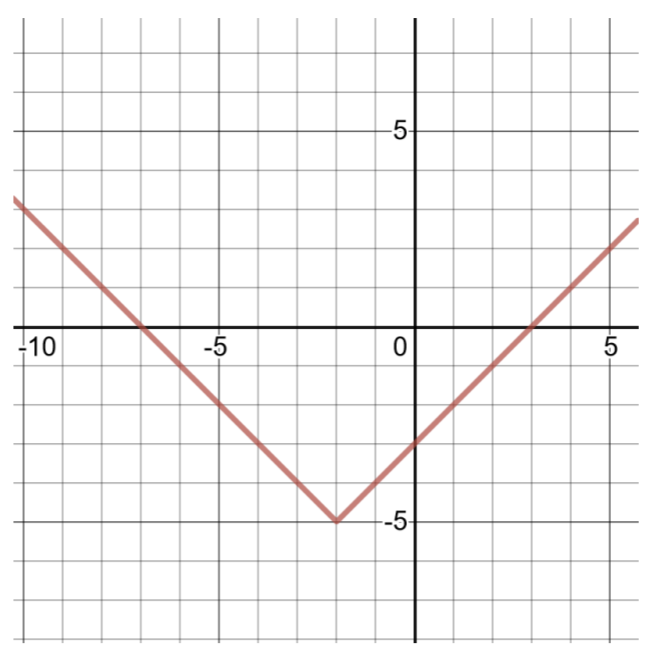
    clipboard_e4ca56e46ab74be7e1b0eaaea223f1a1d.png
    Kielelezo Template:index
    Jedwali la Solutions kwa\(g(x) = \vert x + 2\vert − 5\)
    \(x\) \(g(x)\)
    -3 \(g(−3) = \vert − 3 + 2\vert − 5 = \vert − 1\vert − 5 = 1 − 5 = −4\)
    -2 \(g(−2) = \vert − 2 + 2\vert − 5 = \vert 0\vert − 5 = 0 − 5 = −5\)
    -1 \(g(−1) = \vert − 1 + 2\vert − 5 = \vert 1\vert − 5 = 1 − 5 = −4\)
    Mfano Template:index

    Unda meza ya ufumbuzi na grafu kazi ya thamani kamili:

    \(h(x) = 3\vert x − 5\vert + 1\)

    Suluhisho

    Kulinganisha kazi hii kwa fomu ya jumla ya kazi za thamani kamili (iliyoonyeshwa hapo juu),\(a = 3\),\(h = 5\),\(k = 1\). Vertex ni\((h, k)\) au\((5, 1)\).

    Ili kupata mbili zaidi kuamuru jozi, kuchagua\(x = 4\) na\(x = 6\), kisha compute maadili ya\(h(x)\).

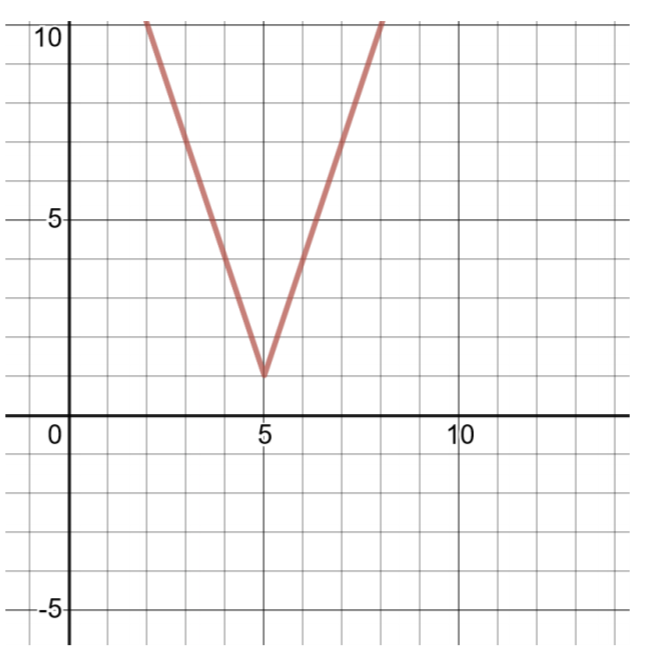
    clipboard_ee43f5a639ef847eb9b27a95bb4052b84.png
    Kielelezo Template:index
    Jedwali la Solutions kwa\(h(x) = 3\vert x − 5\vert + 1\)
    \(x\) \(h(x)\)
    4 \(g(−3) = \vert − 3 + 2\vert − 5 = \vert − 1\vert − 5 = 1 − 5 = −4\)
    5 \(g(−2) = \vert − 2 + 2\vert − 5 = \vert 0\vert − 5 = 0 − 5 = −5\)
    6 \(g(−1) = \vert − 1 + 2\vert − 5 = \vert 1\vert − 5 = 1 − 5 = −4\)
    Mfano Template:index

    Unda meza ya ufumbuzi na grafu kazi ya thamani kamili:

    \(h(x) = \dfrac{1}{2} \vert x − 2\vert + 3\)

    Suluhisho

    Kulinganisha kazi hii kwa fomu ya jumla ya kazi za thamani kamili (iliyoonyeshwa hapo juu),\(a = \dfrac{1}{2} \),\(h = 2\),\(k = 3\). Vertex ni\((h, k)\) au\((2, 3)\).

    Ili kupata mbili zaidi kuamuru jozi, kuchagua\(x = 1\) na\(x = 3\), kisha compute maadili ya\(h(x)\).

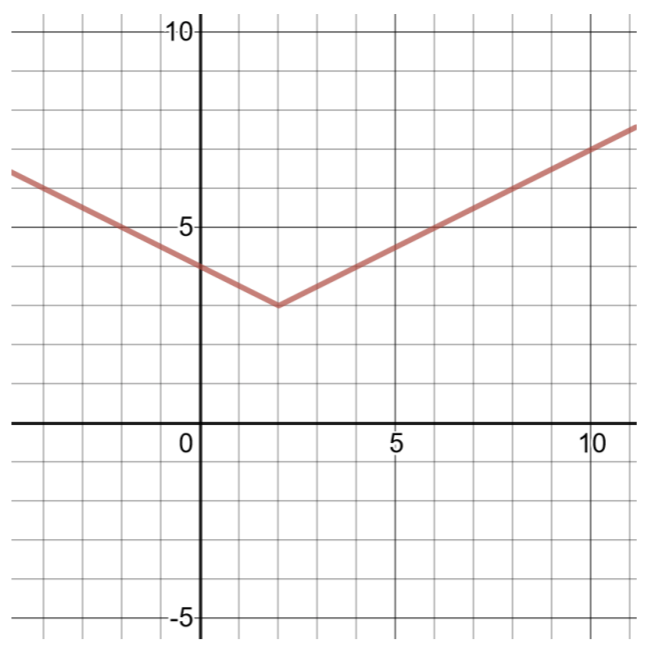
    clipboard_ecc69da60d6771932018e42e8e7a5cdda.png
    Kielelezo Template:index
    Jedwali la Solutions kwa\(h(x) = \dfrac{1}{2} \vert x − 2\vert + 3\)
    \(x\) \(h(x)\)
    1 \(h(1) = \dfrac{1}{2} \vert 1 − 2\vert + 3 = \dfrac{1}{2} \vert − 1\vert + 3 = \dfrac{1}{2} (1) + 3 = 3\dfrac{1}{2}\)
    2 \(h(2) = \dfrac{1}{2} \vert 2 − 2\vert + 3 = \dfrac{1}{2} \vert 0\vert + 3 = 0 + 3 = 3\)
    3 \(h(3) = \dfrac{1}{2} \vert 3 − 2\vert + 3 = \dfrac{1}{2} \vert 1\vert + 3 = \dfrac{1}{2} (1) + 3 = 3\dfrac{1}{2}\)
    Zoezi Template:index

    Unda meza ya ufumbuzi na grafu kazi zifuatazo za thamani kamili:

    1. \(f(x) = \vert x + 6\vert\)
    2. \(g(x) = \dfrac{1}{3} \vert x − 3\vert + 5\)
    3. \(h(x) = 4\vert x + 2\vert + 2\)
    4. \(f(x) = \vert x − 1\vert − 5\)