10.3: Ukosefu wa usawa wa busara
- Page ID
- 164817
Kutatua usawa wa busara unahusisha kutafuta zero za nambari na denominator, kisha kutumia maadili haya kuchunguza mikoa ya kuweka ufumbuzi kwenye mstari wa namba.
Tatua usawa na uandike seti za ufumbuzi katika notation ya muda:
- \(\dfrac{x − 1}{x + 1} ≥ 0\)
- \(\dfrac{2x − 3}{x + 1} ≤ 0\)
- \(\dfrac{x + 2}{x − 2} ≥ 0\)
Suluhisho
- \(\begin{array} &&\dfrac{x − 1}{x + 1} ≥ 0 &\text{Example problem} \\ &\dfrac{x − 1}{x + 1} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).}\\ &x- 1 = 0,\; x = 1 &\ maandishi {Pata zero za namba}\\ &x + 1 = 0, x =\; -1 &\ maandishi {Pata zero za denominator}\ mwisho {safu}\)
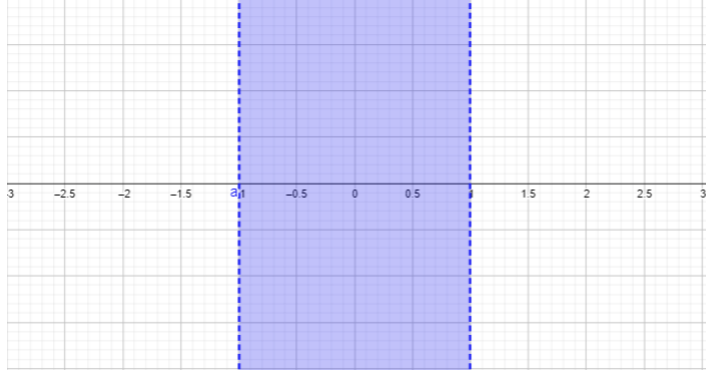
\(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\;\dfrac{−2 − 1}{−2 + 1} = \dfrac{−3}{−1} = 3 ≥ 0 \\ &\text{Replacing \(-2\)kwa\(x\) matokeo katika jibu\(3\), ambayo ni kubwa kuliko au sawa na\(0\). Eneo hili\(x < −1\) linajumuishwa katika seti ya ufumbuzi.}\\ [0.25in] &\ maandishi {Kwa} -1 <x <1,\ maandishi {kuchagua} x = 0.\;\;\ dfrac {0} {0 + 1} =\ dfrac {-1} {1} {1} = -1 <0\\ &\ maandishi {Kubadilisha\(0\)\(x\) matokeo katika jibu\(-1\), ambayo ni chini ya\(0\), si kutimiza kutofautiana kutokana na tatizo.}\\ &\ maandishi {Eneo hili\(−1 < x < 1\) linatengwa na kuweka suluhisho.}\\ [0.25in] &\ maandishi {Kwa} x > 1,\ maandishi {kuchagua} x = 2.\;\;\ dfrac {2 ∙ 1} {2 + 1} =\ dfrac {1} {1} {3} ≥ 0\\ &\ maandishi {Kubadilisha\(2\)\(x\) matokeo katika jibu\(\dfrac{1}{3}\), ambayo ni kubwa kuliko au sawa na\(0\). Mkoa huu\(x > 1\) umejumuishwa katika seti ya ufumbuzi.}\\ [0.25in] & (-Δ, -1) (1, Δ)\\ &\ maandishi {Jibu la mwisho lililoandikwa katika nukuu za muda (angalia sehemu ya Nukuu ya Muda kwa maelezo zaidi).} \ mwisho {safu}\)
- \(\begin{array} &&\dfrac{2x − 3}{x + 1} ≤ 0 &\text{Example problem} \\ &\dfrac{2x − 3}{x + 1} ≤ 0 &\text{The quotient must be less than or equal to \(0\).}\\ &2x - 3 = 0,\; x = 1.5 &\ maandishi {Pata zero za namba}\\ &x + 1 = 0,\; x = -1 &\ maandishi {Pata zero za denominator}\ mwisho {safu}\)
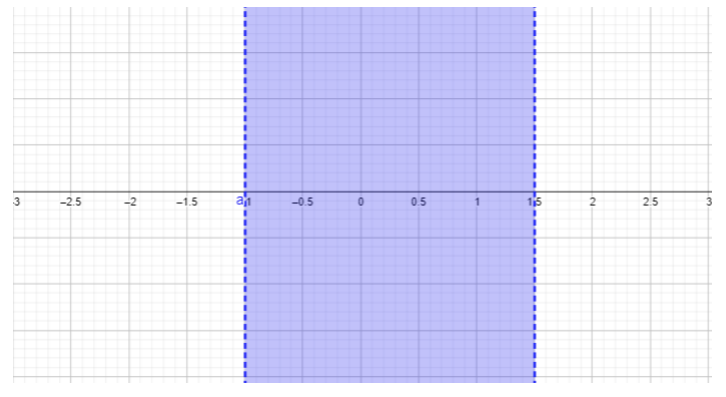
\(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\; \dfrac{2(−2) − 3}{−2 − 1} = \dfrac{−7}{−3} = \dfrac{7}{3} ≥ 0 \\ &\text{Replacing \(-2\)kwa\(x\) matokeo katika jibu\(\dfrac{7}{3}\), ambayo ni kubwa kuliko\(0\), si kutimiza usawa uliotolewa katika tatizo.}\\ &\ maandishi {Eneo hili\(x < −1\) limetengwa na kuweka suluhisho.}\\ [0.25in] &\ maandishi {Kwa} —1 <x <1.5,\ maandishi {chagua} x = 0.\;\\;\ dfrac {2 (0) ∙ 3} {0 - 1} =\ dfrac {-3} {-1} = 3 ≥ 0\\ &\ maandishi {Kubadilisha\(0\)\(x\) matokeo katika jibu\(3\), ambayo ni kubwa kuliko au sawa\(0\), ambayo si kile tatizo linaomba.}\\ &\ maandishi {Eneo hili\(−1 < x < 1.5\) linatengwa katika seti ya suluhisho.}\\ [0.25in] &\ maandishi {Kwa } x > 1,\ maandishi {kuchagua} x = 2.\;\;\ dfrac {2 (2) - 3} {2 ∙ 1} =\ dfrac {1} {1} = 1 ≥ 0\\ &\ maandishi {Kubadilisha\(2\)\(x\) matokeo katika jibu\(1\), ambayo ni kubwa kuliko au sawa\(0\). Eneo hili\(x > 1\) limetengwa katika seti ya suluhisho.}\\ [0.25in] &\\ &\ maandishi {Tatizo hili halina suluhisho. \(\dfrac{2x − 3}{x + 1}\)kamwe kuwa chini ya au sawa na\(0\).} \ mwisho {safu}\)
- \(\begin{array} &&\dfrac{x + 2}{x − 2} ≥ 0 &\text{Example problem} \\ &\dfrac{x + 2}{x − 2} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).}\\ &x + 2 = 0,\;\; x = -1 &\ maandishi {Pata zero za namba}\\ &x- 2 = 0,\;\; x = 2 &\ maandishi {Pata zero za denominator}\ mwisho {safu}\)
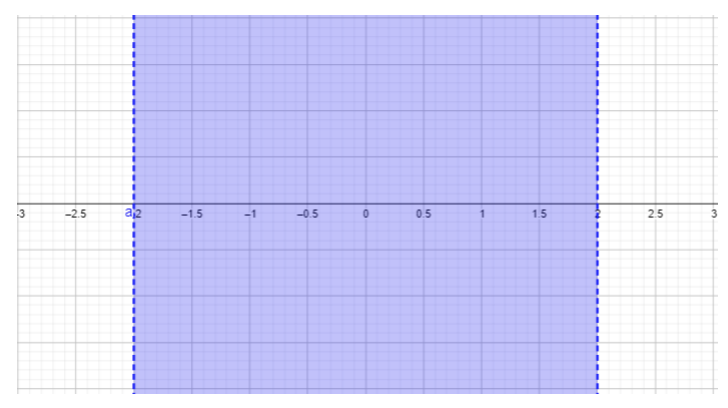
\(\begin{array} &&\text{For } x < −2, \text{ choose } x = −3. \dfrac{−3 + 2}{−3 − 2} = \dfrac{−1}{−5} = \dfrac{1}{5} ≥ 0 \\ &\text{Replacing \(-3\)kwa\(x\) matokeo katika jibu\(\dfrac{1}{5}\), ambayo ni kubwa kuliko au sawa na\(0\). Mkoa huu\(x < −2\) umejumuishwa katika seti ya ufumbuzi.}\\ [0.25in] &\ maandishi {Kwa} -2 <x <2,\ maandishi {kuchagua} x = 0.\;\;\ dfrac {0 + 2} {0 δ 2} =\ dfrac {2} {¯ 2} = -1 <0\\ &\ maandishi {Kubadilisha\(0\)\(x\) matokeo katika jibu\(-1\), ambayo ni chini ya\(0\), si kutimiza kutofautiana kutokana na tatizo.}\\ &\ maandishi {Eneo\(−2 < x < 2\) hili halijumuishwa katika kuweka suluhisho.}\\ [0.25in] &\ maandishi {Kwa} x > 2,\ maandishi {kuchagua} x = 3.\;\;\ dfrac {3 + 2} {3 - 2} =\ dfrac {5} {1} = 5 ≥ 0\\ &\ maandishi {Kubadilisha\(3\) kwa\(x\) matokeo jibu\(5\), ambayo ni kubwa kuliko au sawa na\(0\). Mkoa huu\(x > 2\) umejumuishwa katika seti ya ufumbuzi.}\\ [0.25in] & (-Δ, -1) (2, Δ)\\ &\ maandishi {Jibu la mwisho lililoandikwa katika nukuu za muda (angalia sehemu ya Nukuu ya Muda kwa maelezo zaidi).} \ mwisho {safu}\)
- \(\dfrac{x + 3}{x − 2} ≥ 0\)
- \(\dfrac{x − 2}{x − 1} ≤ 0\)
- \(\dfrac{2x − 1}{x + 2} ≤ 0\)
- \(\dfrac{2x − 3}{x + 1} ≥ 0\)


